计算机中常见的进制

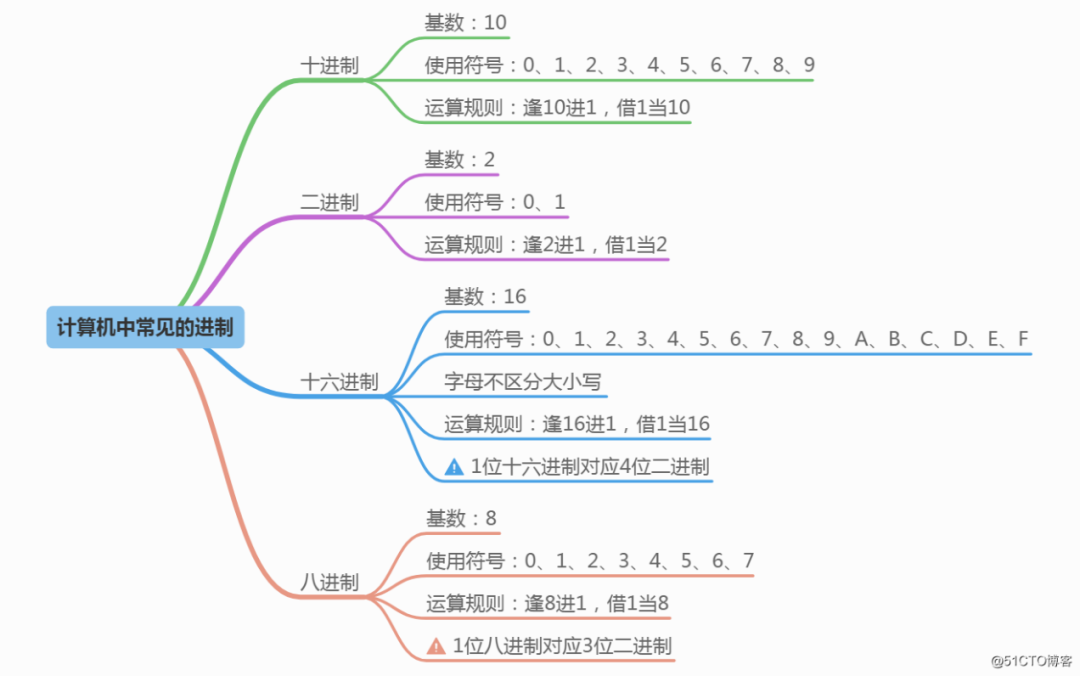
十进制、二进制、十六进制、八进制之间对照表

进制之间的转换

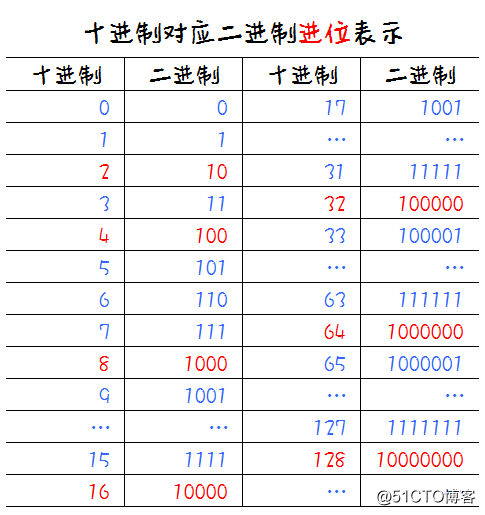
通过上面的十进制对应二进制进位的表示：

当二进制产生增加位数时，相对应十进制数为2、4、8、16、32、64、128，也被称为二进制的位权，根据规律可知二进制每次产生进位，其位权都是前一位位权的两倍。

先了解十进制转十进制：

例如：

二进制数“1101”这个二进制数共有4位，由3个1和1个0组成，从右向左顺序各个位对应十进制的含义为：

第一个1表示：1的个数

第二个0表示：2的个数

第三个1表示：4的个数

第四个1表示：8的个数

(在此可以类比十进制1101，由1个1000，1个100，0个10，1个1组成。)
所以，二进制数1101由1个8，1个4，0个2，1个1组成。按各位的权列出：（1101）2 =1×2^3+1×2^2+0×2^1+1×2^0
= 8+4+0+1
=（13）10

这种权展开式可以很方便将二进制转换为十进制。

同理，将八进制数1024转换为十进制数（1024）8 = 1×8^3+0×8^2+2×8^1+4×8^0
= 512+0+16+4
=（532）10

将十六进制数2B5F转换为十进制数（2B5F）16 = 2×16^3+B×16^2+5×16^1+F×16^0
= 2×16^3+11×16^2+5×16^1+15×16^0
= 8192+2816+80+15
=（11103）10

由此我们可以得到一个非十进制数转换为十进制数的自定义公式：（X）Z = Xn-1×Z^n-1+ Xn-2×Z^n-2+…+ X1×Z^1+X0×Z^0
=（Y）10
X表示一个非二进制（多位），Y表示一个十进制数（多位），Z表示各进制的基数，n表示位数。

十进制转换成二进制、十六进制、八进制

1.十进制转二进制：减法凑数法

也就是说通过十进制数递减二进制的位权，例如：

十进制数：180

二进制位权：128 64  32  16 8  4  2  1

二进制数：10110100

先十进制数（180）减去与十进制数相近的位权数（128），满足不为负进1，剩余52，然后用余数（52）减去第二个最大位权数（64），不满足整减进0，然后用余数（52）减去第三个最大位权数（32），满足不为负进1，剩余20，然后用余数（20）减去第四个最大位权数（16），满足不为负进1，剩余4，然后用余数（4）减去第五个最大位权数（8），不满足整减进0，然后用余数（4）减去第六个最大位权数（4），满足为1，其余都不满足为0.

2.十进制转换为十六进制，采用“除16取余，逆序排列”的方法，十进制转换为八进制采用“除8取余，逆序排列”的方法。

进制之间转换小技巧

1位十六进制等于4位二进制
1位八进制等于3位二进制

由于十六进制和八进制的基数问题（太大或不太好算），它们的“幂次方”和“除基数取余”计算起来比较麻烦，为了方便计算，通常建议先把它们转换位二进制后再继续转换为相应的进制。

例如：16进制（BC）转换成二进制。可以直接转换，B对应11，11转换成二进制为1011，C对应12,12转换二进制为1100，两个相加所得二进制为：10111100