个人主页:C++忠实粉丝
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 C++忠实粉丝 原创分治算法(3)_快速排序_数组中的第K个最大元素
收录于专栏【经典算法练习】
本专栏旨在分享学习算法的一点学习笔记,欢迎大家在评论区交流讨论💌
目录
温馨提示:
1. top k问题
2. 题目链接
3. 题目描述
4. 解法(快速排序)
算法思路:
代码展示:
结果分析:
温馨提示:
该问题是top k问题的一类,top k问题可以使用堆排序和快速排序解决,因为题目要求使用O(N)的时间复杂度解决该问题,所以我这里就直接使用快速排序解决,想看堆排序的宝子们可以取下面的博客查看:
数据结构之二叉树的超详细讲解(2)--(堆的概念和结构的实现,堆排序和堆排序的应用)-CSDN博客
1. top k问题
top k一共有4中类型:
1. 求数据中第k大的数
2. 求数据中第k小的数
3. 求前k大的数
4. 求前k小的数
top k问题在我们生活中还是比较常见的,比如在王者荣耀里面,你是济南市第九吕布,那么就需要系统找到济南市第九荣耀战力的吕布并将其信息打印出来,这样你就能看到你自己是济南市第九吕布了;又比如说:你不满足于济南市第九吕布,你想拿山东省第九吕布,但是你不知道山东省第九吕布的战力是多少,这个时候你就需要查询,山东省前一百吕布的战力,这时候就是top k100问题了
解决top k问题目前有两种方法:
1. 堆排序 时间复杂度O(NlogN)--(这个可以去上面我推荐的博客,讲解的很详细,初中数学知识就行)
2. 快速选择算法 时间复杂度O(N)--(这个的具体证明可以去看算法导论,我数学不太行!)
2. 题目链接
OJ链接 : 数组中的第K个最大元素
3. 题目描述
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入: [3,2,1,5,6,4], k = 2 输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6], k = 4 输出: 4
提示:
1 <= k <= nums.length <= 105-104 <= nums[i] <= 104
4. 解法(快速排序)
算法思路:
这里需要有(数组分三块,随机取key)快速排序的基础,如果还不知道的宝子们可以取看下面的博客:
分治算法(2)_快速排序_排序数组-CSDN博客
在快排中,当我们把数组[分成三块]之后: [l, left][left + 1, right - 1][right, r], 我们可以通过计算每一个区间内的元素[个数],进而推断出我们要找的元素是在[哪一个区间]里面.
那么我们可以直接去[相应的区间]去寻找最终结果就好了.

代码展示:
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
srand(time(NULL));
return qsort(nums, 0, nums.size() - 1, k);
}
int qsort(vector<int>& nums, int l, int r, int k)
{
if(l >= r) return nums[l];
int key = getRandom(nums, l, r);
int i = l, left = l - 1, right = r + 1;
while(i < right)
{
if(nums[i] < key) swap(nums[++left], nums[i++]);
else if(nums[i] == key) i++;
else swap(nums[--right], nums[i]);
}
int b = right - left - 1;
int c = r - right + 1;
if(c >= k) return qsort(nums, right, r, k);
else if(b + c >= k) return key;
else return qsort(nums, l, left, k - b - c);
}
int getRandom(vector<int>& nums, int left, int right)
{
int r = rand();
return nums[left + r % (right - left + 1)];
}
};
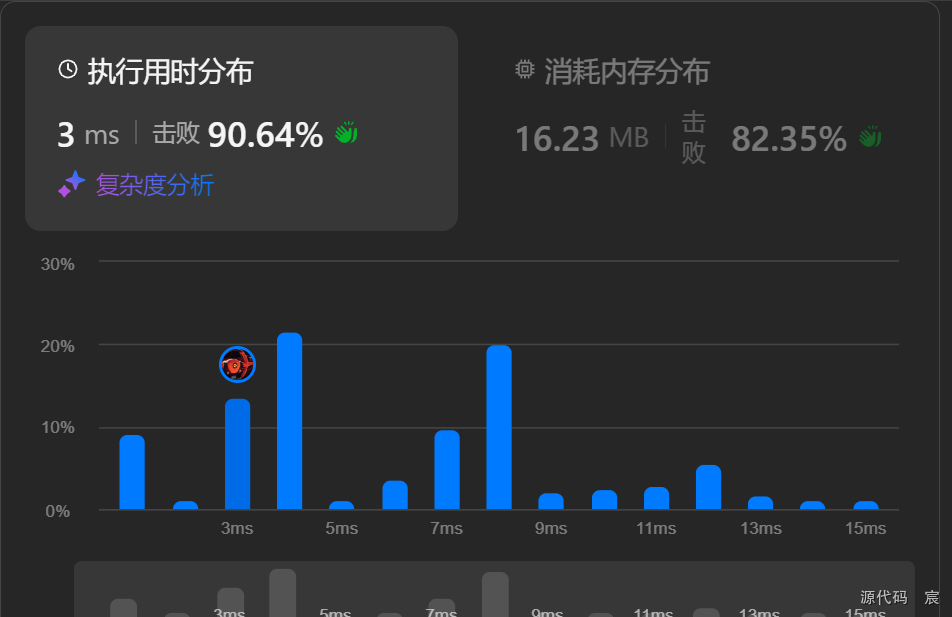
结果分析:
在随机选择基准的情况下,期望的时间复杂度为 O(n)。这是因为在平均情况下,基准会将数组大致分成两半,这样每次递归将处理的元素数量减少大约一半。
由于每次递归的分区工作是线性的(O(n)),整个过程在期望情况下是 O(n) 的。 (具体的证明大家可以看算法导论)