摘要
A算法是一种用于图形搜索的启发式搜索算法,广泛应用于路径规划、游戏AI和机器人导航等领域。本教程将深入介绍A算法的理论基础,展示其在路径规划中的应用,并通过Matlab代码实现A*算法的实际运行。同时,我们将结合实验结果进行分析,帮助读者更好地理解该算法的实际效果。
理论
A*算法结合了Dijkstra算法和启发式搜索的优势,是一种求解最短路径问题的有效方法。其核心思想是通过综合考虑从起点到某一节点的实际代价与该节点到目标的估计代价来选择下一步要扩展的节点,从而在保证路径最优的情况下减少不必要的搜索。
A*算法使用两个函数来评估节点: 𝑔(𝑛):从起点到节点n的实际代价 ℎ(𝑛):从节点n到目标的启发式估计代价
通过总代价函数 𝑓(𝑛)=𝑔(𝑛)+ℎ(𝑛),算法在每一步选择具有最小 𝑓(𝑛)值的节点进行扩展,直至找到目标节点的最优路径。
启发式函数
启发式函数 ℎ ( 𝑛 ) 是A*算法的关键,常用的启发式包括曼哈顿距离和欧几里得距离。选择合适的启发式可以大大提高算法的效率。
实验结果
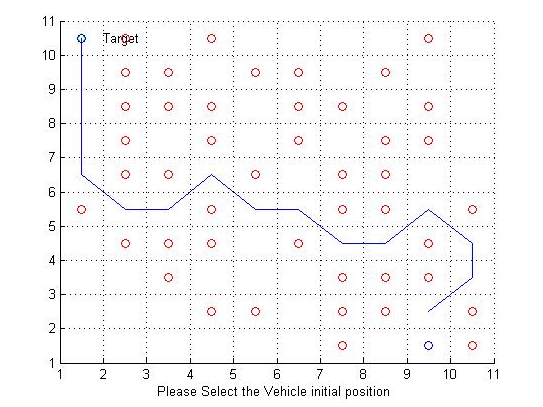
在一个简单的二维网格环境中,我们使用A*算法进行路径规划。实验结果如上图所示,车辆从初始位置(图中蓝色圆圈)开始,沿着蓝色路径最终到达目标位置(图中标记为Target的蓝色圆圈)。红色的圆圈代表障碍物,车辆在路径规划过程中成功避开了所有障碍物。
部分代码
function astar_pathfinding
% 定义网格大小
grid_size = [11, 11];
start_pos = [1, 1];
target_pos = [10, 10];
% 定义障碍物位置
obstacles = [3, 3; 3, 4; 5, 6; 7, 8; 9, 5];
% 初始化open和closed列表
open_list = [];
closed_list = [];
% 其他A*算法逻辑
% 在此处添加g(n)、h(n)计算,以及网格的绘图代码
% 最后绘制路径
figure;
hold on;
plot_path(grid_size, start_pos, target_pos, obstacles);
end
function plot_path(grid_size, start_pos, target_pos, obstacles)
% 在此处定义绘图逻辑,展示网格、障碍物、路径等
plot(target_pos(1), target_pos(2), 'bo', 'MarkerSize', 10, 'DisplayName', 'Target');
plot(obstacles(:, 1), obstacles(:, 2), 'ro', 'MarkerSize', 10, 'DisplayName', 'Obstacle');
% 添加路径的绘制
end
参考文献
❝
Hart, P. E., Nilsson, N. J., & Raphael, B. (1968). A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Transactions on Systems Science and Cybernetics, 4(2), 100-107.
Russell, S., & Norvig, P. (2020). Artificial Intelligence: A Modern Approach (4th ed.). Pearson.
Dechter, R., & Pearl, J. (1985). Generalized Best-First Search Strategies and the Optimality of A*. Journal of the ACM (JACM), 32(3), 505-536.
(文章内容仅供参考,集体效果以图片为准)