强化学习笔记之【DDPG算法】

---

前言：

本文为强化学习笔记第二篇，第一篇讲的是Q-learning和DQN

就是因为DDPG引入了Actor-Critic模型，所以比DQN多了两个网络，网络名字功能变了一下，其它的就是软更新之类的小改动而已

本文初编辑于2024.10.6

CSDN主页：https://blog.csdn.net/rvdgdsva

博客园主页：https://www.cnblogs.com/hassle

博客园本文链接：

---

原论文伪代码

• 上述代码为DDPG原论文中的伪代码

---

DDPG算法

需要先看：

Deep Reinforcement Learning (DRL) 算法在 PyTorch 中的实现与应用【DDPG部分】【没有在选择一个新的动作的时候，给policy函数返回的动作值增加一个噪音】【critic网络与下面不同】

深度强化学习笔记——DDPG原理及实现（pytorch）【DDPG伪代码部分】【这个跟上面的一样没有加噪音】【critic网络与上面不同】

【深度强化学习】(4) Actor-Critic 模型解析，附Pytorch完整代码【选看】【Actor-Critic理论部分】

---

如果需要给policy函数返回的动作值增加一个噪音，实现如下

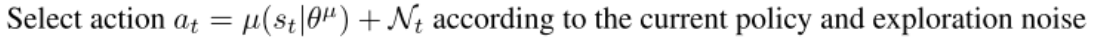
def select_action(self, state, noise_std=0.1):
    state = torch.FloatTensor(state.reshape(1, -1))
    action = self.actor(state).cpu().data.numpy().flatten()
    
    # 添加噪音，上面两个文档的代码都没有这个步骤
    noise = np.random.normal(0, noise_std, size=action.shape)
    action = action + noise
    
    return action

---

DDPG 中的四个网络

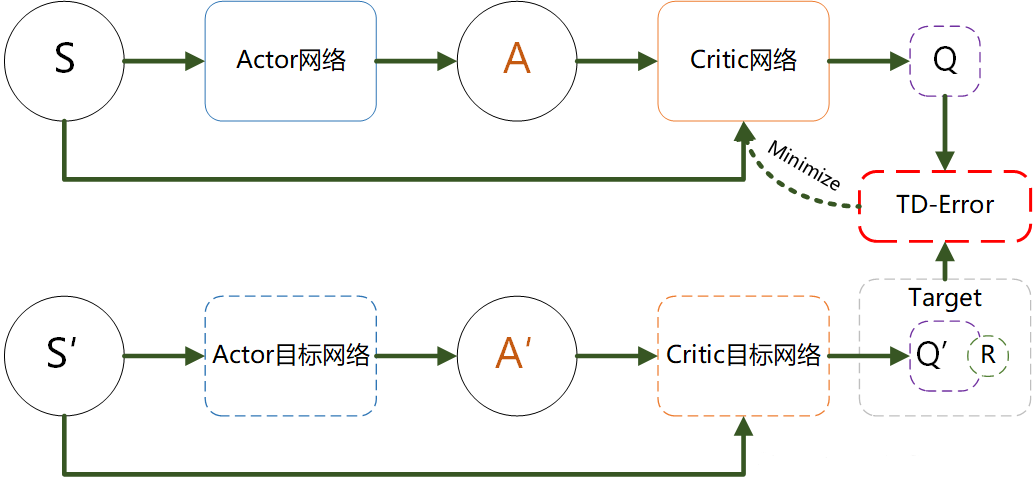
注意！！！这个图只展示了Critic网络的更新，没有展示Actor网络的更新

• Actor 网络（策略网络）：
  • 作用：决定给定状态 ss 时，应该采取的动作 a=π(s)a=π(s)，目标是找到最大化未来回报的策略。
  • 更新：基于 Critic 网络提供的 Q 值更新，以最大化 Critic 估计的 Q 值。
• Target Actor 网络（目标策略网络）：
  • 作用：为 Critic 网络提供更新目标，目的是让目标 Q 值的更新更为稳定。
  • 更新：使用软更新，缓慢向 Actor 网络靠近。
• Critic 网络（Q 网络）：
  • 作用：估计当前状态 ss 和动作 aa 的 Q 值，即 Q(s,a)Q(s,a)，为 Actor 提供优化目标。
  • 更新：通过最小化与目标 Q 值的均方误差进行更新。
• Target Critic 网络（目标 Q 网络）：
  • 作用：生成 Q 值更新的目标，使得 Q 值更新更为稳定，减少振荡。
  • 更新：使用软更新，缓慢向 Critic 网络靠近。

大白话解释：

​ 1、DDPG实例化为actor，输入state输出action
​ 2、DDPG实例化为actor_target
​ 3、DDPG实例化为critic_target，输入next_state和actor_target(next_state)经DQN计算输出target_Q
​ 4、DDPG实例化为critic，输入state和action输出current_Q，输入state和actor(state)【这个参数需要注意，不是action】经负均值计算输出actor_loss

​ 5、current_Q 和target_Q进行critic的参数更新
​ 6、actor_loss进行actor的参数更新

action实际上是batch_action，state实际上是batch_state，而batch_action != actor(batch_state)

因为actor是频繁更新的，而采样是随机采样，不是所有batch_action都能随着actor的更新而同步更新

Critic网络的更新是一发而动全身的，相比于Actor网络的更新要复杂要重要许多

---

代码核心更新公式

$$\begin{gathered} target\underline{}Q=critic\underline{}target(next\underline{}state,actor\underline{}target(next\underline{}state)) \\ target\underline{}Q=reward+(1-done)\times gamma\times target\underline{}Q.detach() \end{gathered}$$

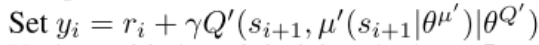
• 上述代码与伪代码对应，意为计算预测Q值

$$\begin{gathered} critic\underline{}loss=MSELoss(critic(state,action),target\underline{}Q) \\ critic\underline{}optimizer.zero\underline{}grad() \\ critic\underline{}loss.backward() \\ critic\underline{}optimizer.step() \end{gathered}$$

• 上述代码与伪代码对应，意为使用均方误差损失函数更新Critic

$$\begin{gathered} actor\underline{}loss=-critic(state,actor(state)).mean() \\ actor\underline{}optimizer.zero\underline{}grad() \\ actor\underline{}loss.backward() \\ actor\underline{}optimizer.step() \end{gathered}$$

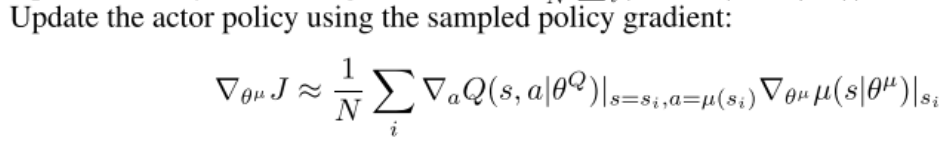
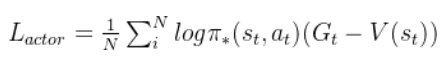
• 上述代码与伪代码对应，意为使用确定性策略梯度更新Actor

$$\begin{gathered} critic\underline{}target.parameters().data=(tau\times critic.parameters().data+(1-tau)\times critic\underline{}target.parameters().data) \\ actor\underline{}target.parameters().data=(tau\times actor.parameters().data+(1-tau)\times actor\underline{}target.parameters().data) \end{gathered}$$

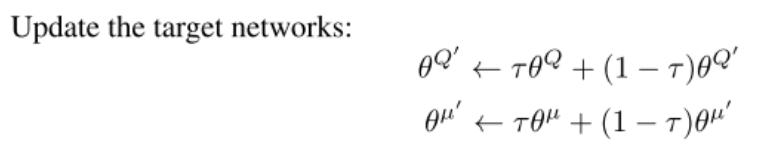
• 上述代码与伪代码对应，意为使用策略梯度更新目标网络

---

Actor和Critic的角色：

• Actor：负责选择动作。它根据当前的状态输出一个确定性动作。
• Critic：评估Actor的动作。它通过计算状态-动作值函数（Q值）来评估给定状态和动作的价值。

更新逻辑：

• Critic的更新：
  1. 使用经验回放缓冲区（Experience Replay）从中采样一批经验（状态、动作、奖励、下一个状态）。
  2. 计算目标Q值：使用目标网络（critic_target）来估计下一个状态的Q值（target_Q），并结合当前的奖励。
  3. 使用均方误差损失函数（MSELoss）来更新Critic的参数，使得预测的Q值（target_Q）与当前Q值（current_Q）尽量接近。
• Actor的更新：
  1. 根据当前的状态（state）从Critic得到Q值的梯度（即对Q值相对于动作的偏导数）。
  2. 使用确定性策略梯度（DPG）的方法来更新Actor的参数，目标是最大化Critic评估的Q值。

---

个人理解：

DQN算法是将q_network中的参数每n轮一次复制到target_network里面

DDPG使用系数$$\tau$$来更新参数，将学习到的参数更加soft地拷贝给目标网络

DDPG采用了actor-critic网络，所以比DQN多了两个网络