

1. 二分查找
704. 二分查找

这是一道单纯的朴素二分模版题,当 left == right 时的这种情况也是需要考虑的,因为不排除数组中只有一个数的情况,或者是二分到数组中只剩一个数的情况,所以循环条件要写 left <= right
class Solution {
public int search(int[] nums, int target) {
int left = 0, right = nums.length - 1, mid = 0;
while (left <= right) {
mid = (left + right) / 2;
if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else {
return mid;
}
}
return -1;
}
}2. 在排序数组中查找元素的第一个和最后一个位置
34. 在排序数组中查找元素的第一个和最后一个位置

求区间左端点 :

可以把区间分为两部分,一部分是 x < t 的情况,另一部分就是 x >= t 的情况,由于 x < t 中不包含答案,所以可以把 left = mid + 1,跳出这部分,同理,由于答案在右半部分,所以 right = mid ,就不能跳出这个区间了,又因为这个区间都是 x >= t 的,所以最后也一定会找到左端点
关于循环条件:

当最后需要执行更新 right 的操作时,如果说此时 left 和 right 指向了同一个位置,那么算出来的 mid 还是这个位置,更新的 right 还是此时的位置,会一直重复这个操作,导致死循环,同时无论是有结果的情况还是没有结果的情况,当 left 和 right 指向了同一个位置这个时候都需要退出循环,所以说循环条件就不能包含等于了
求中点的操作:
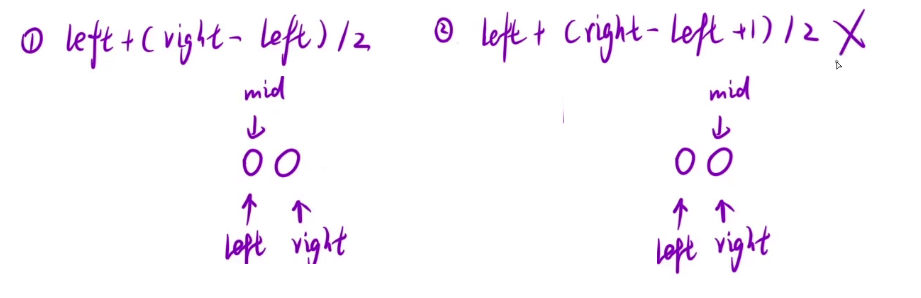
当数组是偶数的时候,中点的位置会有两个,如果加一就是右边的中点,不加就是左边的中点,因为上面 right 是移动到 mid 的位置的,如果这里按照右边的中点就会死循环,按照左边的中点就可以正常的退出循环
求区间右端点:
和求左端点相反,这里是把小于等于目标值分为一个区间,大于目标值分为一个区间,所以说 left 就只能移动到 mid 的位置了,如果移动到 mid + 1 就会错过答案,同理 right 是需要移动到 mid - 1 的位置去寻找答案的

关于循环条件:
这里的条件和区间左端点是一样的,都是不能写等号
求中点的操作:
由于这一次需要将 left 移动到 mid 的位置,所以说就不能求左边的中点了,需要求右边的中点才能退出循环

之后再处理一下特殊情况就可以了:当数组为空时或者循环结束后没有找到目标值的情况
class Solution {
public int[] searchRange(int[] nums, int target) {
int[] ans = new int[2];
if (nums.length == 0) {
ans[0] = -1;
ans[1] = -1;
return ans;
}
int left = 0, right = nums.length - 1, mid = 0;
//左端点
while (left < right) {
mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else {
right = mid;
}
}
if (nums[right] == target) {
ans[0] = right;
} else {
ans[0] = -1;
}
//left = 0;
right = nums.length - 1;
while (left < right) {
mid = left + (right - left + 1) / 2;
if (nums[mid] > target) {
right = mid - 1;
} else {
left = mid;
}
}
if (nums[right] == target) {
ans[1] = right;
} else {
ans[1] = -1;
}
return ans;
}
}3. x 的平方根
69. x 的平方根

题目要求小数部分要舍去,要求的是算术平方根,平方之后是小于等于 x 的,也就是要求区间的左端点的问题
class Solution {
public int mySqrt(int x) {
if (x < 1) return 0;
long left = 0, right = x, mid = 0;
while (left < right) {
mid = left + (right - left + 1) / 2;
if (mid * mid <= x) {
left = mid;
} else {
right = mid - 1;
}
}
return (int) left;
}
}4. 搜索插入位置
35. 搜索插入位置

无论是要插入的位置还是找到目标值,所在的区间都是 >= 目标值的区间,也就是查找区间左端点的情况,最后如果找到了目标值直接返回下标,找不到就返回下标 + 1,也就是要插入的位置
class Solution {
public int searchInsert(int[] nums, int target) {
if(nums[0] > target) return 0;
int left = 0, right = nums.length - 1, mid = 0;
while (left < right) {
mid = left + (right - left + 1) / 2;
if (nums[mid] > target) {
right = mid - 1;
} else {
left = mid;
}
}
if (nums[left] == target)
return left;
else
return left + 1;
}
}5. 山脉数组的峰顶索引
852. 山脉数组的峰顶索引

这道题并不像上面的题一样,要查找的区间是有序的,这道题虽然不是有序的但是具有二段性,所以也可以使用二分来解决
关于峰值:第一个前一个元素大于后一个元素的位置

根据上面的分法就是求区间的右端点,如果把峰值分到右区间就是求区间左端点,这里以右端点为例:
class Solution {
public int peakIndexInMountainArray(int[] arr) {
if (arr.length == 1) return 0;
int left = 0, right = arr.length - 1, mid = 0;
while (left < right) {
mid = left + (right - left + 1) / 2;
if (arr[mid] > arr[mid - 1]) {
left = mid;
} else {
right = mid - 1;
}
}
return left;
}
}6. 162. 寻找峰值
162. 寻找峰值

这道题和上一道题不同的是会有多个峰值,需要找到其中的一个峰值,虽然有很多峰值,但是经过分析,还是可以发现存在二段性:
首先是可能会有三种情况的

无论是哪种情况,都可以找到以下的状态

也就可以有以下的结论:
nums[mid] > nums[mid + 1] : right = mid
nums[mid] < nums[mid + 1] : left = mid + 1
class Solution {
public int findPeakElement(int[] nums) {
int left = 0, right = nums.length - 1, mid = 0;
while (left < right) {
mid = left + (right - left) / 2;
if (nums[mid] < nums[mid + 1]) {
left = mid + 1;
} else {
right = mid;
}
}
return left;
}
}7. 寻找旋转排序数组中的最小值
153. 寻找旋转排序数组中的最小值

每一次旋转就是把最后一位的元素移动到第一位,题目就是求旋转后的数组中的最小值,这道题也可以分析出二段性,由于题目中已经明确指出了是互不相同的数组,所以可以得出以下结论:

将数组可以分为两段,左边的半段都是比右边的大的,所以答案也就在右边,就需要让 left = mid + 1,同理,如果 mid 落到右边,那么就是 right = mid ,从而不错过答案
class Solution {
public int findMin(int[] nums) {
int n = nums.length;
int left = 0, right = n - 1, mid = 0;
while (left < right) {
mid = left + (right - left) / 2;
if (nums[mid] > nums[n - 1]) {
left = mid + 1;
} else {
right = mid;
}
}
return nums[right];
}
}上面是以 nums[n - 1] 作为对照,也可以把第一个元素作为对照,不过此时就需要考虑翻转之后的数组如果一直都是递增的特殊情况
class Solution {
public int findMin(int[] nums) {
int n = nums.length;
if (nums[n - 1] > nums[0]) {
return nums[0];
}
int left = 0, right = n - 1, mid = 0;
while (left < right) {
mid = left + (right - left) / 2;
if (nums[mid] < nums[0]) {
right = mid;
} else {
left = mid + 1;
}
}
return nums[right];
}
}8. LCR 173. 点名
LCR 173. 点名

这道题是有多种解法的:
第一种:哈希表,把 0 ~ n - 1 的数丢到哈希表中,然后遍历求解
第二种:直接遍历
第三种:位运算
第四种:高斯求和,相减
上面的解法时间复杂度都是 O (n) 的,用二分的话就需要去找它的二段性
可以通过下标入手,左边区间下标是对应的,右边的是数组元素比下标大的

此外,还有一种特殊情况,就是数组中的元素和下标都是对应的,此时缺少的数字就是 n
class Solution {
public int takeAttendance(int[] records) {
int left = 0, right = records.length - 1, mid = 0;
if(records[right] == right) return right+1;
while (left < right) {
mid = left + (right - left) / 2;
if (records[mid] == mid) {
left = mid + 1;
} else {
right = mid;
}
}
return left;
}
}



















