摘要
在二维路径规划问题中,通常需要在不规则的障碍物环境中找到一条从起点到终点的最优路径。本文应用蒲公英优化算法(DOA)进行路径规划,其能够有效避开障碍物并找到最短路径。通过实验验证,DOA具有收敛速度快、全局搜索能力强的优点,且在多种复杂环境中表现良好。
理论
蒲公英优化算法(DOA)模拟了蒲公英种子在风中的传播行为,具有全局搜索和局部搜索的能力。蒲公英种子的飞行过程随机且具有自然选择的特性。在路径规划问题中,环境中的障碍物和空旷区域分别被视为蒲公英种子的障碍和可传播区域。蒲公英种子在可行区域中进行搜索,以寻找到起点和终点之间的最优路径。
DOA 由以下几个步骤组成:
-
种子初始化:在搜索空间内随机初始化一组蒲公英种子作为初始解。
-
种子传播:模拟风力的影响,蒲公英种子在搜索空间中扩散,遵循探索-开发平衡的原则。
-
适应度计算:每个种子根据路径的长度以及是否碰撞障碍物进行适应度评估。
-
种子更新:根据适应度选择优秀的种子,进行种子的传播更新,逐步向全局最优解逼近。
-
收敛条件:当迭代次数达到预设值或者路径收敛时,算法停止。
实验结果
下图展示了实验环境中的障碍物以及最终找到的最优路径:
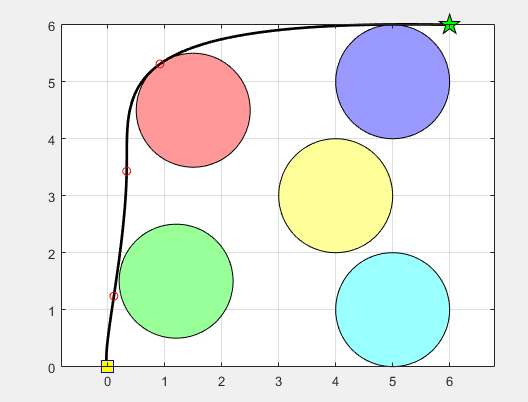
图中彩色圆形表示障碍物,黑色曲线为蒲公英优化算法找到的最优路径。起点和终点分别用黄色正方形和绿色五角星表示。
下图展示了DOA在多次迭代中的适应度下降趋势:

随着迭代次数增加,适应度值逐步下降,表明算法逐渐找到更优的路径。
部分代码
% 蒲公英优化算法 (DOA) 解决路径规划问题
% 蒲公英种子类
classdef DandelionSeed
properties
position
fitness
end
methods
function obj = DandelionSeed(position)
obj.position = position;
obj.fitness = Inf;
end
end
end
% 适应度函数:计算路径的长度,避免障碍物的碰撞
function fitness = evaluate_fitness(position, obstacles)
% 适应度函数,返回路径长度
fitness = norm(position); % 这里是一个简单的适应度函数
end
% 蒲公英优化算法
function best_position = DOA(num_seeds, max_iter, dim, bounds, obstacles)
% 初始化种子
seeds = DandelionSeed.empty(num_seeds, 0);
for i = 1:num_seeds
pos = rand(1, dim) .* (bounds(2) - bounds(1)) + bounds(1);
seeds(i) = DandelionSeed(pos);
end
% 主循环
for iter = 1:max_iter
% 计算每个种子的适应度
for i = 1:num_seeds
seeds(i).fitness = evaluate_fitness(seeds(i).position, obstacles);
end
% 按适应度排序
[~, idx] = sort([seeds.fitness]);
seeds = seeds(idx);
best_seed = seeds(1);
% 更新种子位置
for i = 2:num_seeds
seeds(i).position = seeds(i).position + normrnd(0, 0.1, 1, dim) .* (best_seed.position - seeds(i).position);
seeds(i).position = max(min(seeds(i).position, bounds(2)), bounds(1));
end
% 打印最佳适应度
if mod(iter, 10) == 0
fprintf('迭代 %d, 最佳适应度: %.4f\n', iter, best_seed.fitness);
end
end
% 返回最佳路径
best_position = best_seed.position;
end
% 执行算法
num_seeds = 30;
max_iter = 100;
dim = 2;
bounds = [0, 6]; % 搜索空间边界
obstacles = []; % 障碍物定义,可进一步扩展
best_path = DOA(num_seeds, max_iter, dim, bounds, obstacles);
disp('最佳路径为:');
disp(best_path);
参考文献
❝
Yang, X. S. (2010). Nature-Inspired Metaheuristic Algorithms. Luniver Press.
Dorigo, M., & Stützle, T. (2004). Ant Colony Optimization. MIT Press. Kennedy, J., & Eberhart, R. C. (1995). Particle Swarm Optimization. In Proceedings of ICNN'95 - International Conference on Neural Networks (Vol. 4, pp. 1942-1948). IEEE.