一:斐波那契词序列
题目描述
编写一个程序,生成斐波那契词序列的前n个元素。 斐波那契词序列是一个词序列,其中每个词是通过连接前两个词形成的。 它以斐波那契序列命名,因为它是以类似的方式创建的,但是我们不是加数字,而是连接字符串或符号。
比如: 从两个单字母词开始,传统上是a和b。连接最后两个词以形成下一个词。 因此,斐波那契词序列的前几个词是:a,b,ba,bab,babba
定义函数generate_fibonacci_word(),接受一个参数n(整数)。
如果n小于2,函数应返回invalid。
对于n的其他值,生成斐波那契词序列到第n项,并逗号, 分隔的字符串返回。
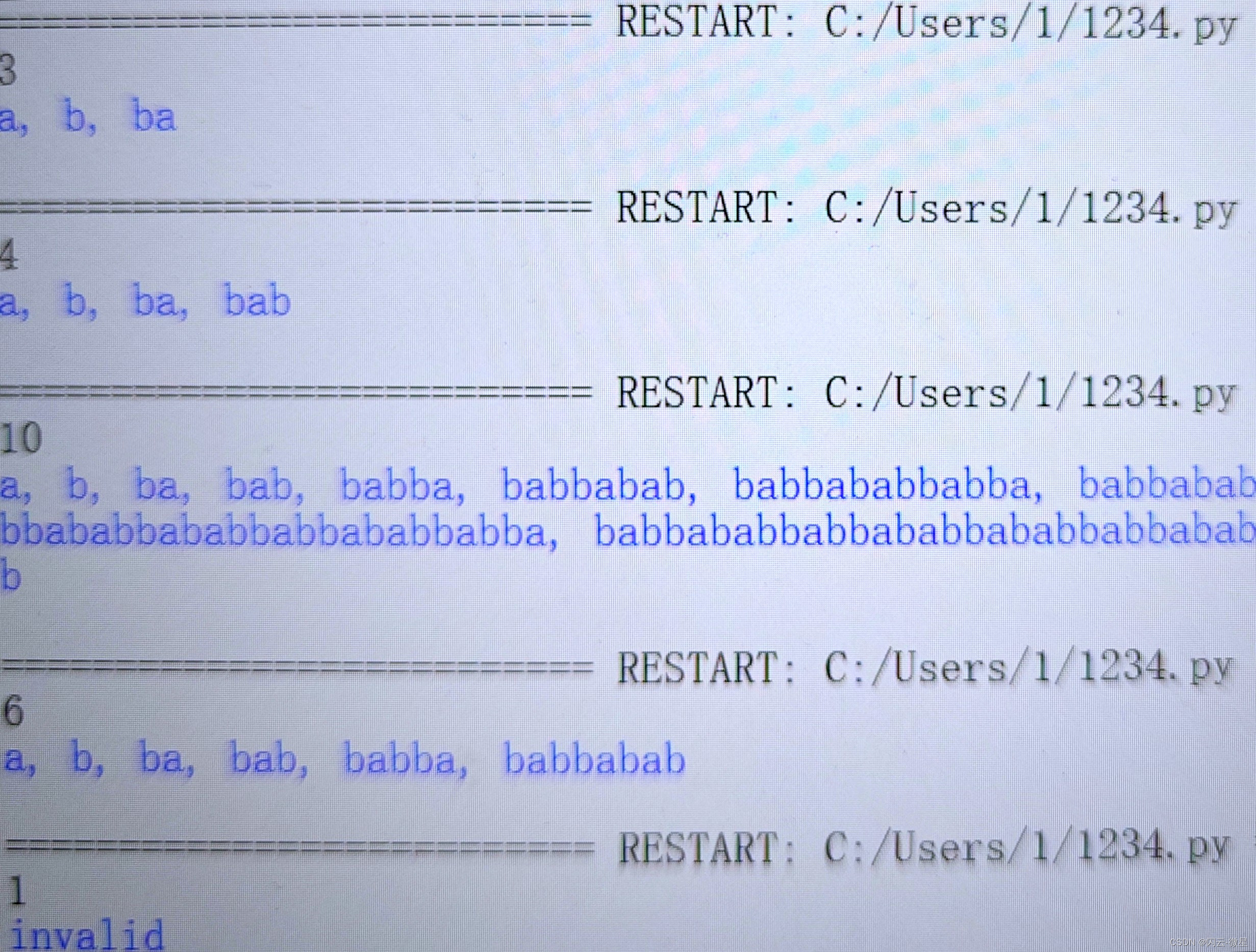
示例输入
5
示例输出
a, b, ba, bab, babba
n小于2,返回invalid。
join()方法可以将列表转换为逗号分隔的字符串,但单词之间为逗号和空格。比如", ".join(["a", "b", "c"])返回"a, b, c"。
来源/分类(难度系数:二星)
算法 机器翻译
完整代码展示:
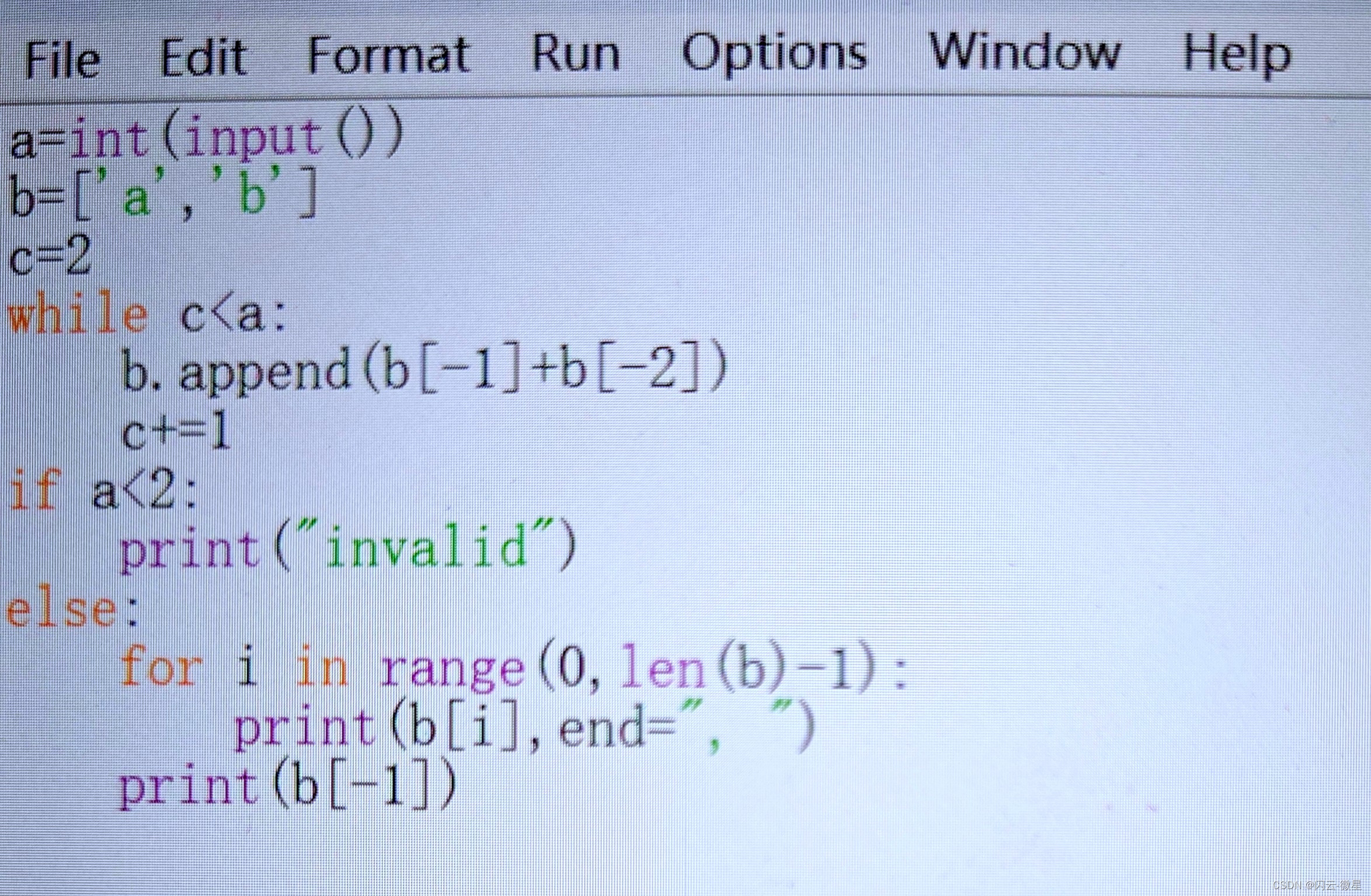
a=int(input())
b=['a','b']
c=2
while c<a:
b.append(b[-1]+b[-2])
c+=1
if a<2:
print("invalid")
else:
for i in range(0,len(b)-1):
print(b[i],end=", ")
print(b[-1])
a=int(input())
b=['a','b']
c=2
while c<a:
b.append(b[-1]+b[-2])
c+=1
if a<2:
print("invalid")
else:
for i in range(0,len(b)-1):
print(b[i],end=", ")
print(b[-1])
代码解释:
“a=int(input()) ”,导入用户输入的斐波那契词序列的元素数量a。
“b=['a','b']
c=2
while c<a:
b.append(b[-1]+b[-2])
c+=1 ”,建立一个空列表b,b的前两项为a,b。令c为循环密码子,初始值为2,当c<a时:将b的最后两个元素连接后添加进b中。每循环一次:c+1,直至c==a,跳出整个while循环。
“if a<2:
print("invalid")
else:
for i in range(0,len(b)-1):
print(b[i],end=", ")
print(b[-1]) ”,判断a是否小于2,如果是:则打印”invalid”,否则依次打印b中元素,每两个元素之间插入一个逗号。
运行效果展示:
二:最大回文乘积
题目描述:
编写一个程序,找出两个n位数乘积中的最大回文数。
定义函数largest_palindrome_product,该函数接受一个参数n。
在函数内部,返回两个n位数的最大回文乘积。
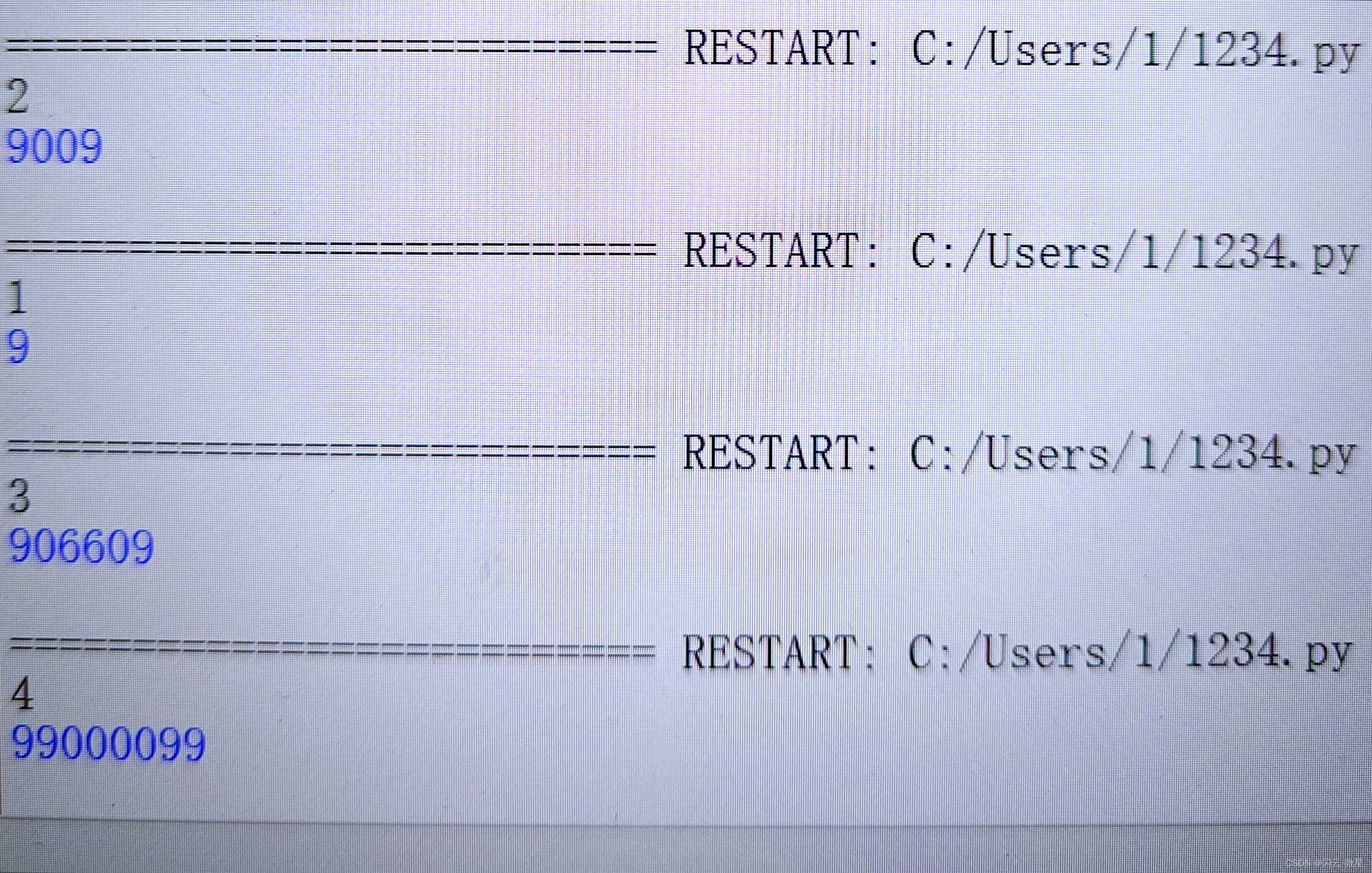
示例输入
2
示例输出
9009
解释: 两个2位数的最大回文乘积是9009 = 91 * 99。
回文数是指从前往后读和从后往前读都一样的数。例如,12321是回文数,而12345不是回文数。
注意两个1位数的最大回文乘积是9 = 1 * 9。
来源/分类(难度系数:二星)
循环结构 数学思维
完整代码展示:
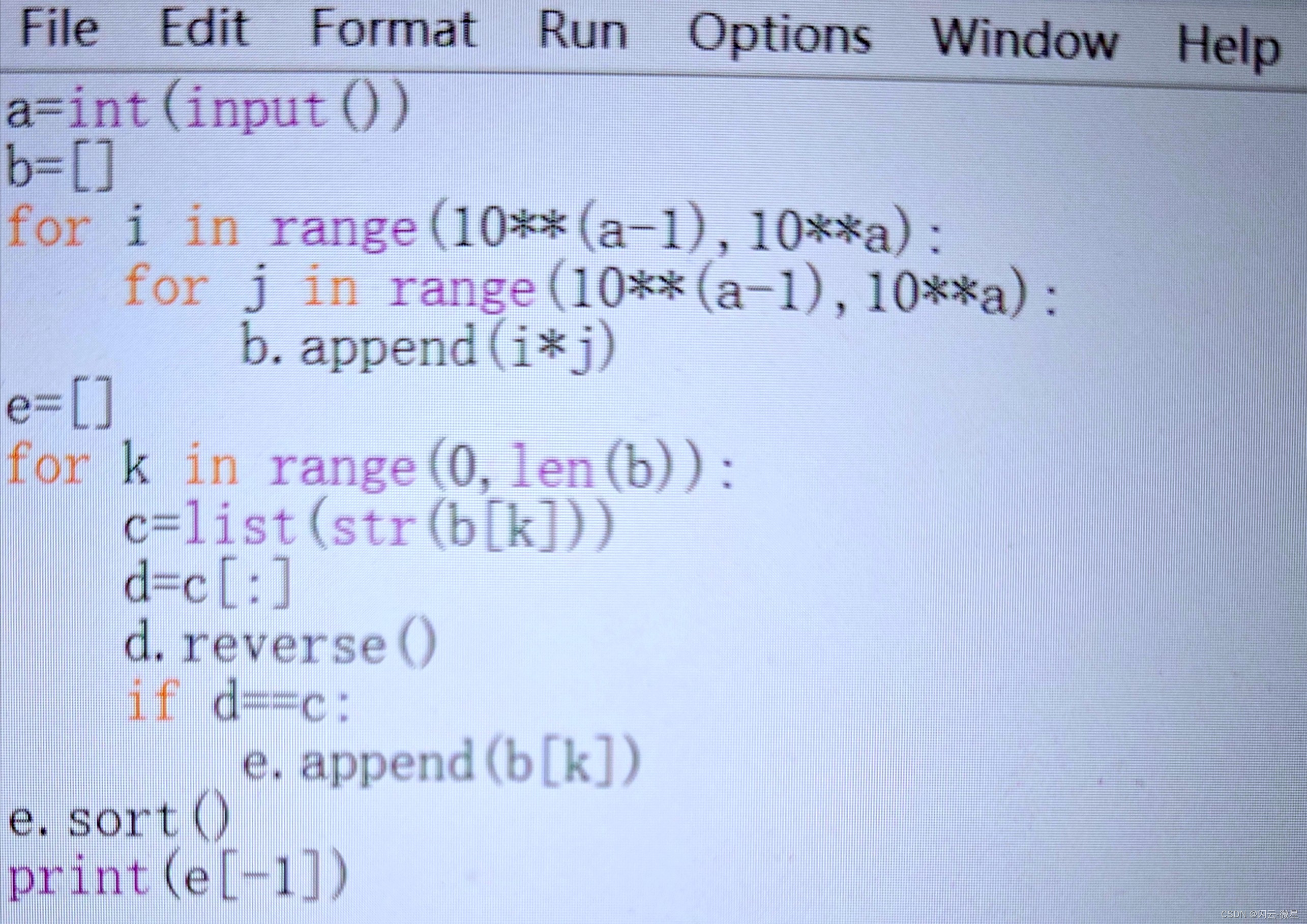
a=int(input())
b=[]
for i in range(10**(a-1),10**a):
for j in range(10**(a-1),10**a):
b.append(i*j)
e=[]
for k in range(0,len(b)):
c=list(str(b[k]))
d=c[:]
d.reverse()
if d==c:
e.append(b[k])
e.sort()
print(e[-1])
a=int(input())
b=[]
for i in range(10**(a-1),10**a):
for j in range(10**(a-1),10**a):
b.append(i*j)
e=[]
for k in range(0,len(b)):
c=list(str(b[k]))
d=c[:]
d.reverse()
if d==c:
e.append(b[k])
e.sort()
print(e[-1])
代码解释:
”a=int(input()) ”,导入用户输入的参数n。
“b=[]
for i in range(10**(a-1),10**a):
for j in range(10**(a-1),10**a):
b.append(i*j) ”,建立一个空列表b,接着依次遍历10的a-1次方到10的a次方-1的数i和j,再将i*j的值添加进b中。
“e=[]
for k in range(0,len(b)):
c=list(str(b[k]))
d=c[:]
d.reverse()
if d==c:
e.append(b[k]) ”,建立一个空列表e,接着依次遍历b中元素:将该元素转换为字符串后储存在列表c中,再将c复制后赋给d,将d反转,判断d是否等于c,如果相同:将b[k]添加进e中。
“e.sort()
print(e[-1]) ”,对e中元素进行升序排序,最后打印列表e的最后一个元素。
运行效果展示:
三:求最大最小k个元素
题目描述
编写一个程序,从一个元组中提取最大和最小的K个元素。
定义函数extract_max_min(),有两个参数:input_tuple(一个整数元组)和k(要提取的数量)。
在函数内部,从input_tuple中找到k个最小和k个最大的元素。
返回一个包含提取元素的元组,其中前k个元素是最小的,后k个元素是最大的。
示例输入
4 2 7 9 10 45 3 83
示例输出
(2, 3, 4, 9, 10, 45)
解释: 由于测试输入中k的值为3,因此提取并以元组的形式返回最小的3个数(2,3和4)和最大的3个数(9,10和45)
保证k小于等于input_tuple的长度。
来源/分类(难度系数:二星)
循环结构 递归
完整代码展示:
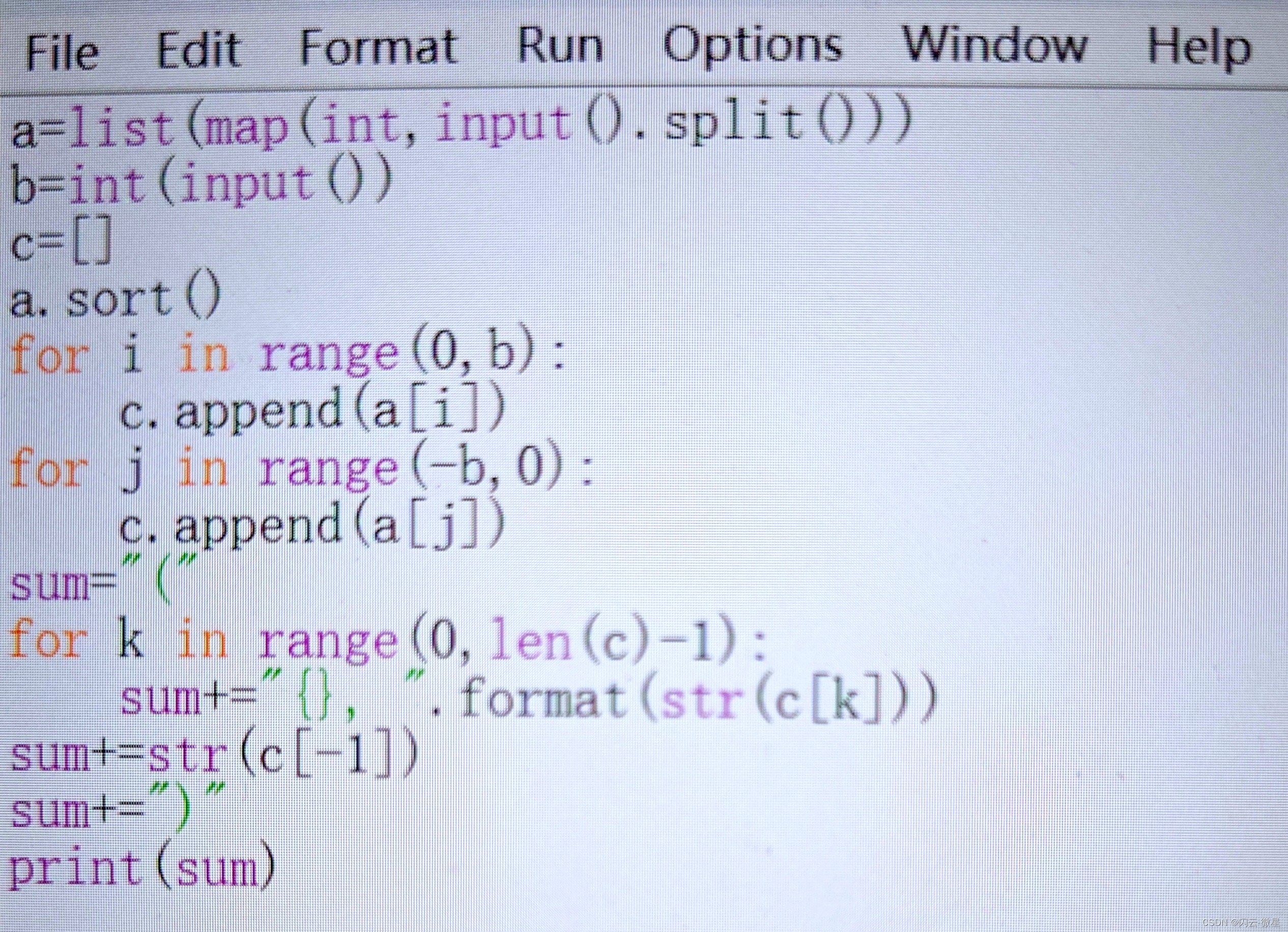
a=list(map(int,input().split()))
b=int(input())
c=[]
a.sort()
for i in range(0,b):
c.append(a[i])
for j in range(-b,0):
c.append(a[j])
sum="("
for k in range(0,len(c)-1):
sum+="{}, ".format(str(c[k]))
sum+=str(c[-1])
sum+=")"
print(sum)
a=list(map(int,input().split()))
b=int(input())
c=[]
a.sort()
for i in range(0,b):
c.append(a[i])
for j in range(-b,0):
c.append(a[j])
sum="("
for k in range(0,len(c)-1):
sum+="{}, ".format(str(c[k]))
sum+=str(c[-1])
sum+=")"
print(sum)
代码解释:
“a=list(map(int,input().split())) ”,导入用户输入的元组元素,并将其储存在列表a中。
“b=int(input()) ”,导入用户输入的需要提取的元组元素数量b。
“c=[]
a.sort()
for i in range(0,b):
c.append(a[i]) ”,建立一个空列表c,接着对a中元素进行升序排序。遍历0~b-1的数字i,将a[i]添加进c中。
“for j in range(-b,0):
c.append(a[j]) ”,遍历-b~-1的数字j,将a[j]添加进c中。
“sum="("
for k in range(0,len(c)-1):
sum+="{}, ".format(str(c[k]))
sum+=str(c[-1])
sum+=")" ”,建立一个字符串sum,包含小括号左半部分。接着依次遍历c中除最后一个元素的其余元素,利用sum连接起来,且每两个元素之间插入一个逗号。连接c中最后一个元素,最后连接小括号右半部分。
“print(sum) ”,打印sum的最终结果。
运行效果展示:
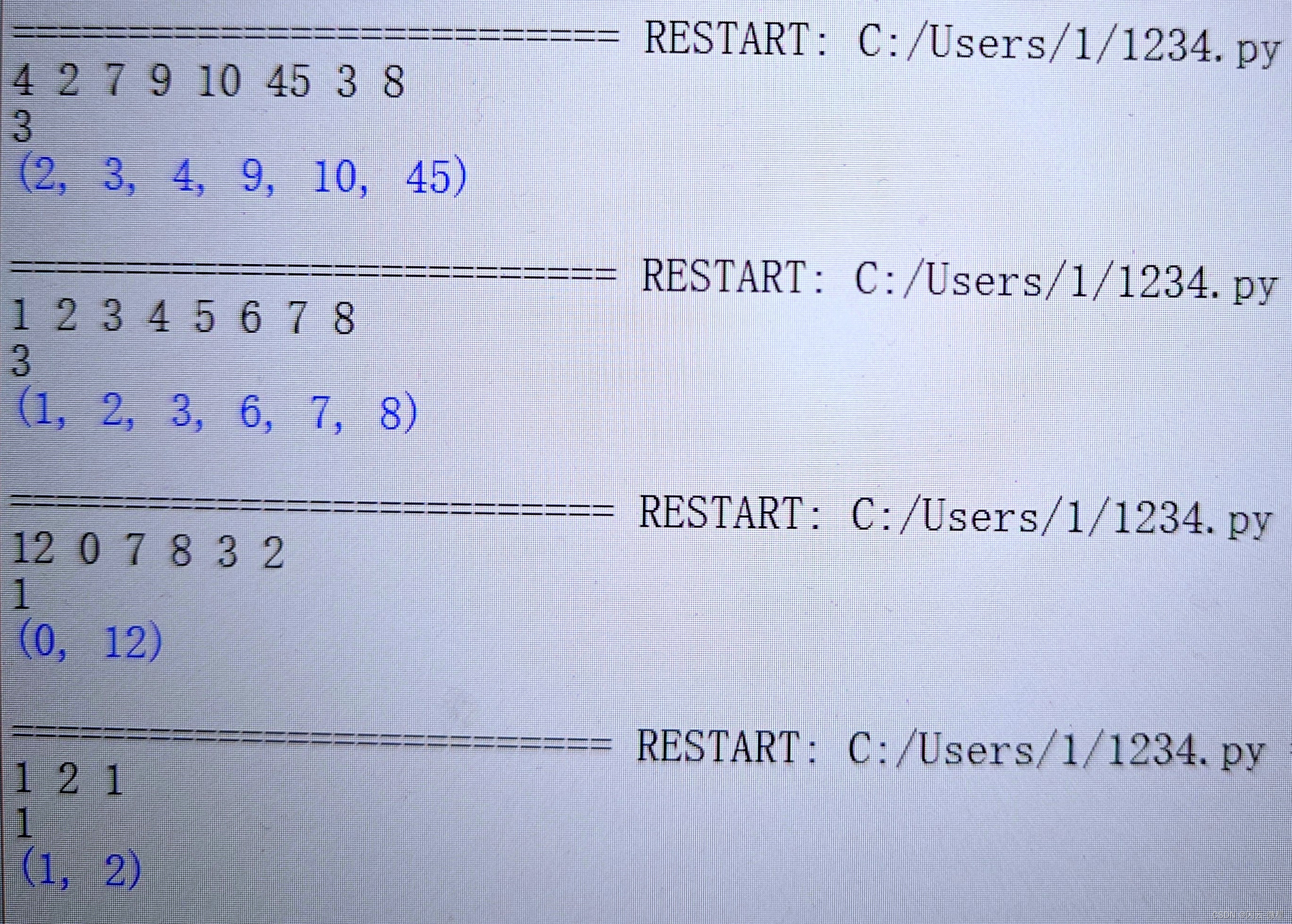
(声明:以上内容均为原创)