二分查找，顾名思义，就是每次筛选能晒掉一半的数据。 二分查找主要用在数据有单调特性或者有二段性。

二分查找，虽然是基础算法，但是需要注意的细节非常的多，这里主要提供两种二分查找的思路，可以根据自己的理解程度去进行选择。

一、思路一：常规思路

二分查找需要注意的就是两点：一是循环条件，二是求中点的方法。

// 循环条件
left < right;
left <= right;

// 求中点的方法
(left + right) / 2; // 可能有数据溢出的风险
left + (right - left) / 2;
left + (right - left + 1) / 2;

1、寻找固定值

/**************************  
写法一：
循环条件：left <= right
寻找中间值：上述的寻找中间值方法都行
left 和 right 的初始值是 0 和 nums.size() - 1
**************************/
int BinarySearch(vector<int> nums, int target)
{
    sort(nums.begin(), nums.end());
	int left = 0, right = nums.size() - 1; // 注意
	
	while (left <= right) // 注意
	{
		int mid = (left + right) / 2;
		if (nums[mid] < target)
			left = mid + 1;
		else if (nums[mid] > target)
			right = mid - 1;
		else
			return nums[mid] == target ? mid : -1;
	}
	return -1;
}

/**************************  
写法二：
循环条件：left < right
寻找中间值：上述的寻找中间值方法都行
left 和 right 的初始值是 0 和 nums.size()
**************************/
int BinarySearch(vector<int> nums, int target)
{
    sort(nums.begin(), nums.end());
	int left = 0, right = nums.size();

	while (left < right)
	{
		int mid = (left + right) / 2;
		if (nums[mid] < target)
			left = mid + 1;
		else if (nums[mid] > target)
			right = mid;
		else
			return nums[mid] == target ? mid : -1;
	}
	return -1;
}

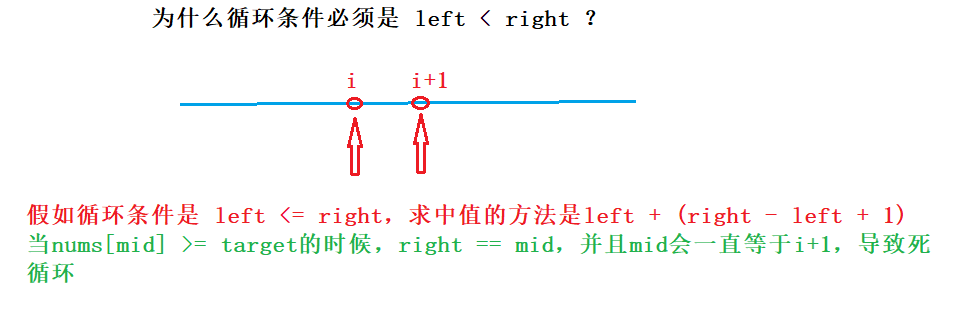
2、寻找左边界

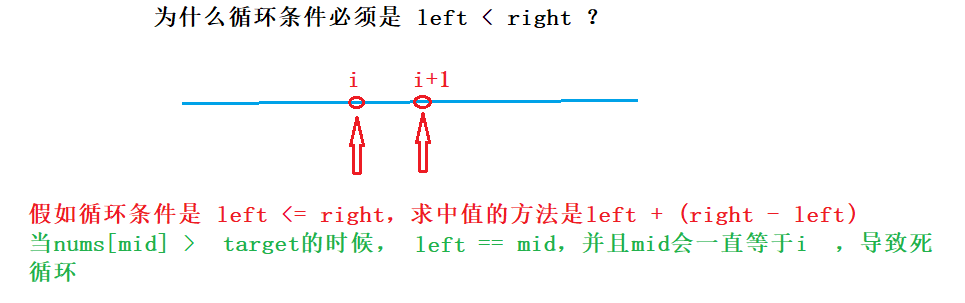
循环条件：left < right（不能有等于，这样会导致死循环）

求中点的方法：left + (right - left) / 2（这个和另外一个防止溢出的方法，唯一不同的是当数组元素个数是偶数的时候中间值是左边还是右边的问题）

int FindLeft(vector<int>& nums, int target)
    {
        int l = 0, r = nums.size() - 1;
        while (l < r)
        {
            int mid = l + (r - l) / 2;
            if (nums[mid] < target) l = mid + 1;
            else r = mid;
        }
        if (nums[l] != target) return -1;
        return l;
    }

3、寻找右边界

循环条件：left < right（不能有等于，这样会导致死循环）

求中点的方法：left + (right - left + 1) / 2

int FindRight(vector<int>& nums, int target)
    {
        int l = 0, r = nums.size() - 1;
        while (l < r)
        {
            int mid = l + (r - l + 1) / 2;
            if (nums[mid] <= target) l = mid;
            else r = mid - 1;
        }
        if (nums[r] != target) return -1;
        return r;
    }

二、思路二：红蓝法二分

大家可以看看我之前的文章

https://blog.csdn.net/qq_73435980/article/details/134771467

三、模板题

1、二分查找

https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/description/给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

class Solution {
public:
    int search(vector<int>& nums, int target) {
        sort(nums.begin(), nums.end());
        int left = 0, right = nums.size();

        while (left < right) {
            int mid = (left + right) / 2;
            if (nums[mid] < target)
                left = mid + 1;
            else if (nums[mid] > target)
                right = mid;
            else
                return nums[mid] == target ? mid : -1;
        }
        return -1;
    }
};

2、在排序数组中查找元素的第一个和最后一个位置

https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/description/

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：

输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：

输入：nums = [], target = 0
输出：[-1,-1]

class Solution {
public:
    int FindLeft(vector<int>& nums, int target)
    {
        int l = 0, r = nums.size() - 1;
        while (l < r)
        {
            int mid = l + (r - l) / 2;
            if (nums[mid] < target) l = mid + 1;
            else r = mid;
        }
        if (nums[l] != target) return -1;
        return l;
    }
    int FindRight(vector<int>& nums, int target)
    {
        int l = 0, r = nums.size() - 1;
        while (l < r)
        {
            int mid = l + (r - l + 1) / 2;
            if (nums[mid] <= target) l = mid;
            else r = mid - 1;
        }
        if (nums[r] != target) return -1;
        return r;
    }
    vector<int> searchRange(vector<int>& nums, int target) {
        if (nums.size() == 0) return { -1, -1 };
        int a = FindLeft(nums, target);
        int b = FindRight(nums, target);

        vector<int> ans = { a, b };
        return ans;
    }
};