学习? 学个P!☺ — 亮剑 李云龙
🏰代码及环境配置:请参考 环境配置和代码运行!
本节提供了3次样条曲线的代码测试
python3 tests/curves/cubic_spline.py
2.2.c.1 3次样条曲线代码实现
CubicSpline1D实现了1维的3次样条曲线, 需要输入一组离散点. CubicSpline1D会计算两个点之间的3次多项式.
class CubicSpline1D:
def __init__(self, x, y):
h = np.diff(x)
if np.any(h < 0):
raise ValueError("x coordinates must be sorted in ascending order")
self.a, self.b, self.c, self.d = [], [], [], []
self.x = x
self.y = y
self.nx = len(x) # dimension of x
# calc coefficient a
self.a = [iy for iy in y]
# calc coefficient c
A = self.__calc_A(h)
B = self.__calc_B(h, self.a)
self.c = np.linalg.solve(A, B)
# calc spline coefficient b and d
for i in range(self.nx - 1):
d = (self.c[i + 1] - self.c[i]) / (3.0 * h[i])
b = 1.0 / h[i] * (self.a[i + 1] - self.a[i]) - h[i] / 3.0 * (
2.0 * self.c[i] + self.c[i + 1]
)
self.d.append(d)
self.b.append(b)
它同样提供了计算0阶, 1阶, 2阶导数的接口
def calc_position(self, x):
if x < self.x[0]:
return None
elif x > self.x[-1]:
return None
i = self.__search_index(x)
dx = x - self.x[i]
position = (
self.a[i] + self.b[i] * dx + self.c[i] * dx**2.0 + self.d[i] * dx**3.0
)
return position
def calc_first_derivative(self, x)
if x < self.x[0]:
return None
elif x > self.x[-1]:
return None
i = self.__search_index(x)
dx = x - self.x[i]
dy = self.b[i] + 2.0 * self.c[i] * dx + 3.0 * self.d[i] * dx**2.0
return dy
def calc_second_derivative(self, x):
if x < self.x[0]:
return None
elif x > self.x[-1]:
return None
i = self.__search_index(x)
dx = x - self.x[i]
ddy = 2.0 * self.c[i] + 6.0 * self.d[i] * dx
return ddy
对于2维的3次样条曲线, 只需要在(x, y)上分别构造参数方程即可.
2.2.c.2 3次样条曲线代码测试
- 1维的3次样条曲线
在main_1d()中, 我们提供了一组1维点, 构造CubicSpline1D即可.
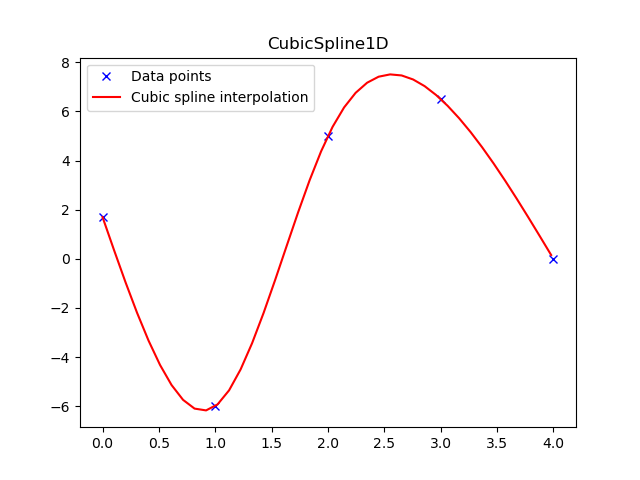
- 2维的3次样条曲线
在main_2d()中, 我们提供了一组(x,y)点, 分别在x,y上构造CubicSpline1D.
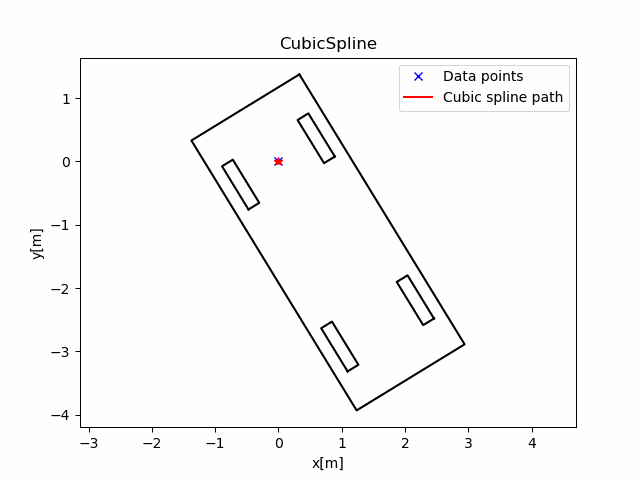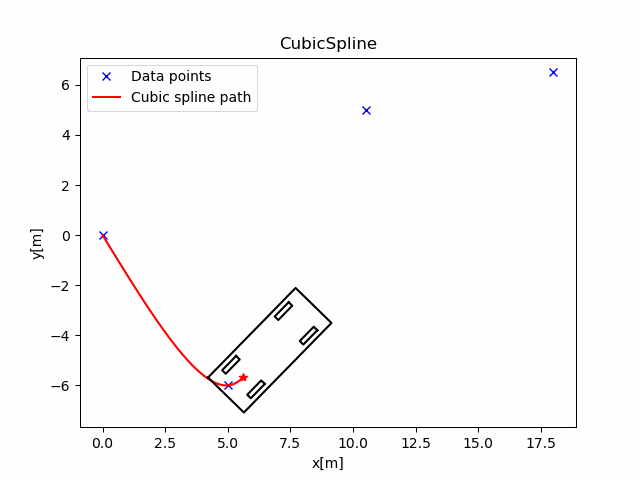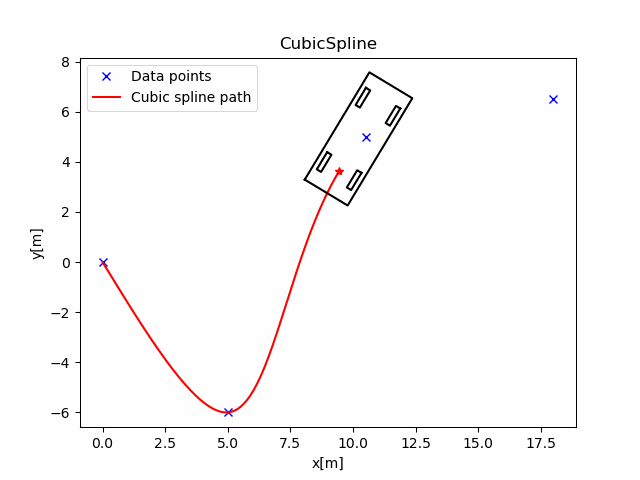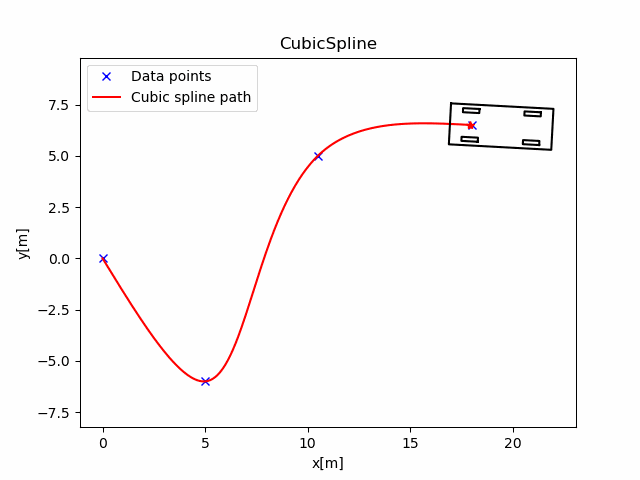
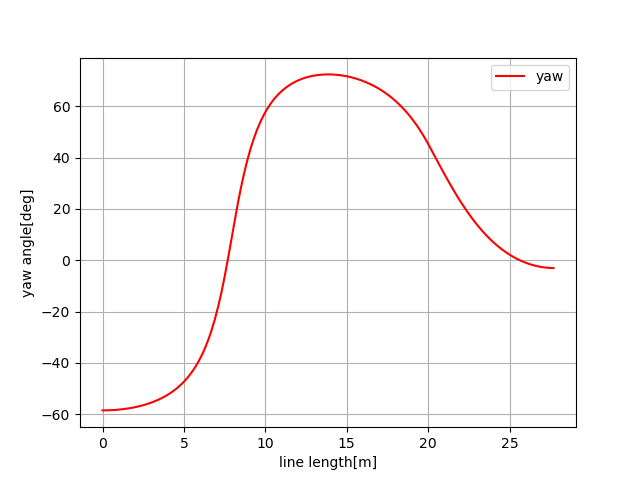
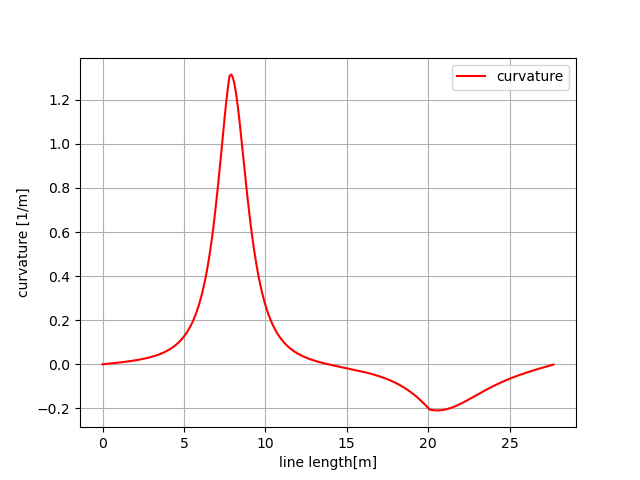
这条曲线的航向角和曲率如下图:
🏎️自动驾驶小白说官网:https://www.helloxiaobai.cn
🐮GitHub代码仓:https://github.com/Hello-Xiao-Bai/Planning-XiaoBai!
🔥课程答疑,面试辅导:https://shop380995420.taobao.com
🌠代码配合官网教程食用更佳!
🚀知乎,微信,知识星球全平台同号!