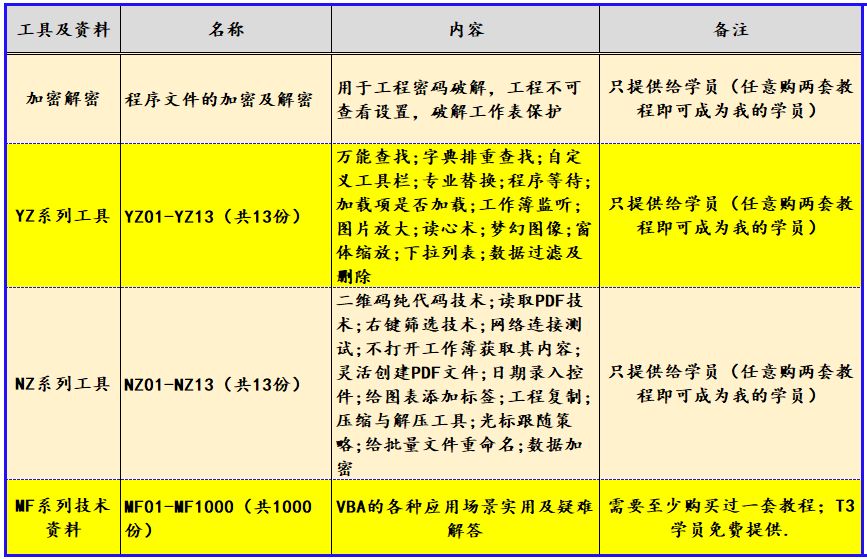
快速幂

题目

• 三个整数 a、b 和 m，计算 a 的 b 次幂对 m 取模的结果
• a^b a^c= a^b+c
• (a+b)|m=(a|m+b|m)|m。|为数学中的求模运算符，相当于c语言中的%。
• (ab)|m=(a|mb|m)|m

算法

• 二分法求幂。
• 先求a^b的一半，并缓存起来。
• 避免每次的半值计算。
• 中间值求模，避免结果太大而溢出。

代码

#include<iostream>
using namespace std;
int power(int a, int b,int m){
	if(b==1)
		return a%m;
	int temp=power(a,b/2,m);//b的奇、偶，影响分支走向 
	if(b%2==0)
		return temp*temp%m;//b是偶数，则分支对半分 
	else
		return temp*temp%m*a%m;//b是奇数，则分成temp和temp+1，故需再*a 
}
int main(){
	cout<<power(2,9,2)<<endl;
	return 0;
} 

大整数乘法

题目

• 乘数(位数很多)*被乘数(位数很多)。

思路

• 乘法是递归计算，加法也是递归计算。
• 乘法是折半递归，当位数大于4的时候，就进行折半拆分，直到位数<=4时进行计算（递归出口）。
• 乘法递归函数需调用加法，被乘数的位数大于4位拆分成高位和低位，商=高位*乘数+低位*乘数，计算的时候高位的低数位补0。
• 加法递归出口为位数都<=8位时，计算返回。否则将被加数和加数从右边的8位开始拆分相加。拆分成低位和高位，分别相加，高位+高位，低位+低位，然后将结果合并。
• 高位、低位合并的时候采用流的方式，注意低位的前导0会影响结果。如果低位的和为3位数，流进stringstream中时，因缺0而少5位使结果出错，故需补0，凑成8位。
• 低位相加的和产生进位时保留右8位，但高位的结果需补进位的值1。

代码

#include<iostream>
#include<string>
#include<sstream>
using namespace std;
string add(string s1,string s2){
	if(s1.size()<=8 && s2.size()<=8){
		stringstream ss;
		int a,b;
		string s;
		ss<<s1<<" "<<s2;
		ss>>a>>b;
		ss.clear();
		ss<<a+b;
		ss>>s;
		return s;
	}
	string s1a="0";
	string s1b=s1;
	if(s1.size()>8){
		s1a=s1.substr(0,s1.size()-8);
		s1b=s1.substr(s1.size()-8);
	}
	string s2a="0";
	string s2b=s2;
	if(s2.size()>8){
		s2a=s2.substr(0,s2.size()-8);
		s2b=s2.substr(s2.size()-8);
	}
	string t=add(s1b,s2b);
	while(t.size()<8)
		t="0"+t;
	if(t.size()>8)
		return add(add(s1a,s2a),"1") +t.substr(1);
	return add(s1a,s2a)+t;
} 
string multi(string s1,string s2){
	if(s1.size()<=4 && s2.size()<=4){
		stringstream ss;
		int a,b;
		string s;
		ss<<s1<<" "<<s2;
		ss>>a>>b;
		ss.clear();
		ss<<a*b;
		ss>>s;
		return s;
	}
	if(s1.size()<=4) return multi(s2,s1);
	int k=s1.size()/2;
	string s1a=s1.substr(0,k);
	string s1b=s1.substr(k);
	return add(multi(s1a,s2)+string(s1b.size(),'0'),multi(s1b,s2));
} 
int main(){
	cout<<multi("123456789","12345678912345678")<<endl;
	return 0;
}