我们可以比 O(nlog(n)) 更快地排序。
长按关注《Python学研大本营》,加入读者群,分享更多精彩 扫码关注《Python学研大本营》,加入读者群,分享更多精彩
介绍
我将介绍一种我称之为 groupSort 的排序方法。我没有直接解决排序问题,而是明确地作为排序问题,而是向左走了一步,选择解决另一种问题——分组问题。这样做,这为一个更简单的排序问题设置了条件,完成后,我得到了一个原始值的排序数组。
在更详细地讨论我的想法之前,让我直接跳到几个琐碎的例子,尽管如此,立即说明我的观点:我们可以比 O(nlog(n)) 更快地排序。
平凡排序
如果我有 1000 万行数据,其中每个元素取值 1 或 0,那么在对这 1000 万个项目进行排序时,我是否可以做得比O(nlog(n))时间复杂度更好?
答案是显而易见的,当我们面对数据中的二进制分类时,我们每天都会做的事情。我只需要使用一些控制结构遍历所有项目,将项目分成 1 和 0 组。然后,我可以将 0 组放在 1 组之前,例如将它们连接到一个数组中。我没有设置时间复杂度。我有一个步骤要解决时间复杂度O(n)(为每个项目确定 1 或 0)。我的清理步骤是O(1)的时间复杂度(将两组组合成一个数组)。总而言之,这使我的总体时间复杂度为O(n)。
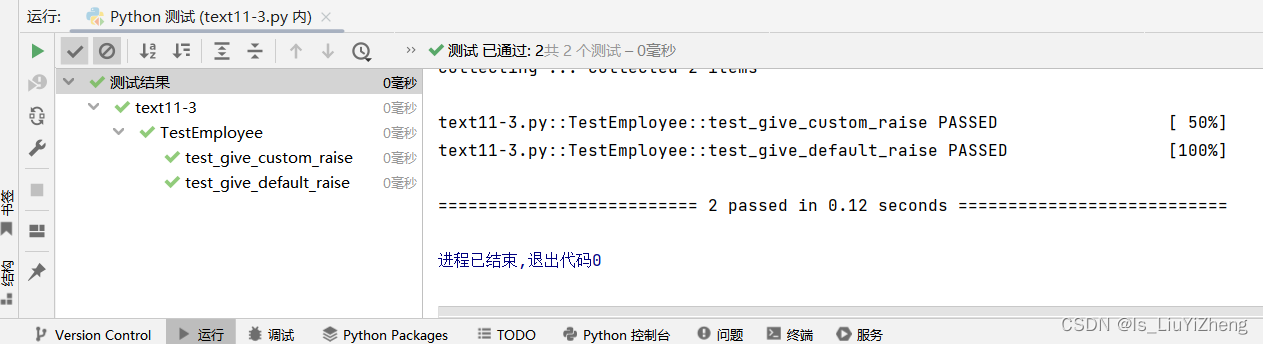
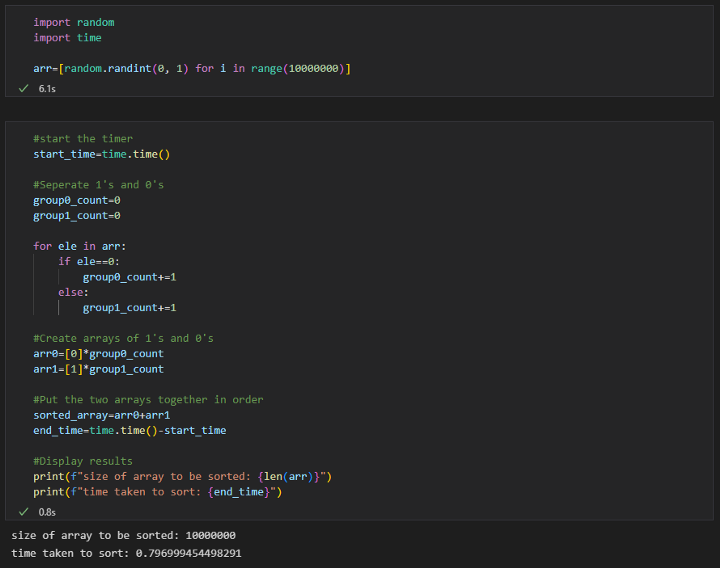
下面是与使用 mergeSort 进行排序相比的基本逻辑流程和运行此逻辑所用时间的屏幕截图。
将包含 1000 万个项目的数组分成 1 和 0,然后将它们连接到一个数组中:
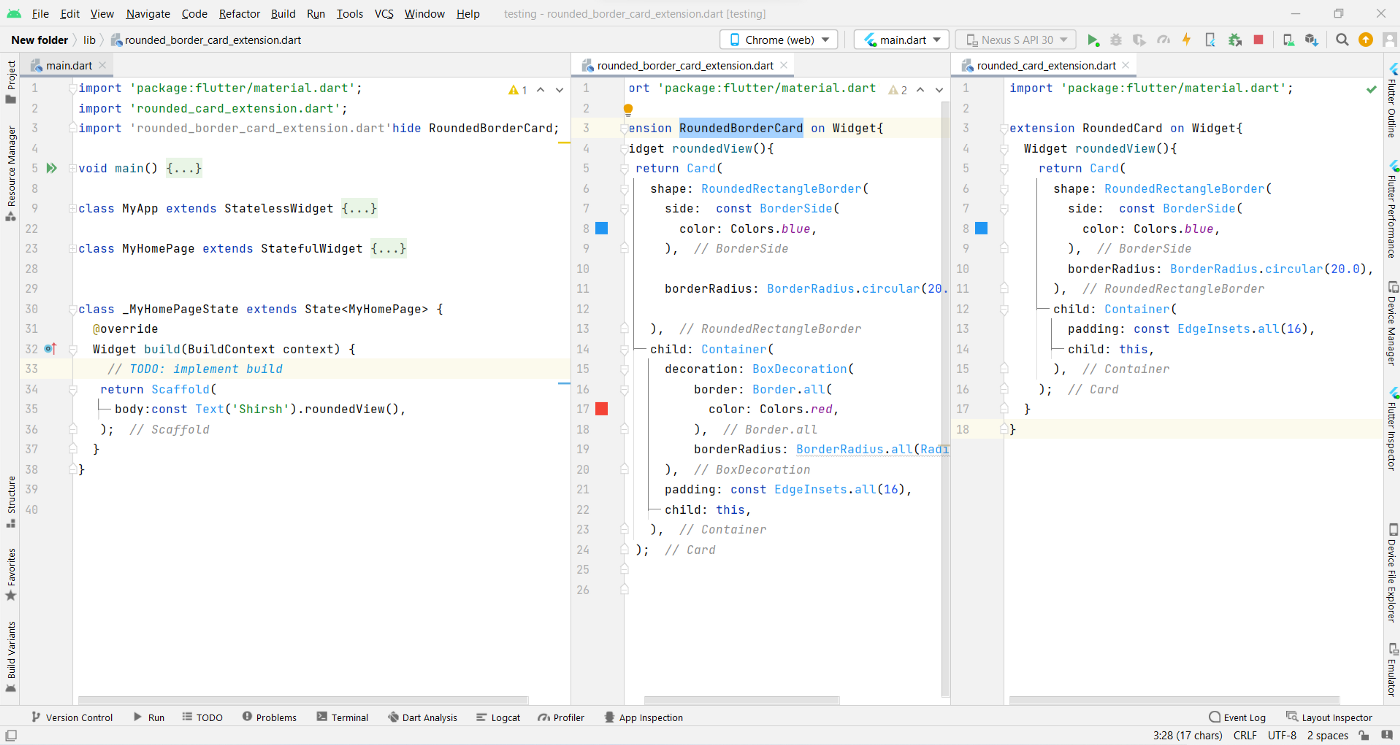
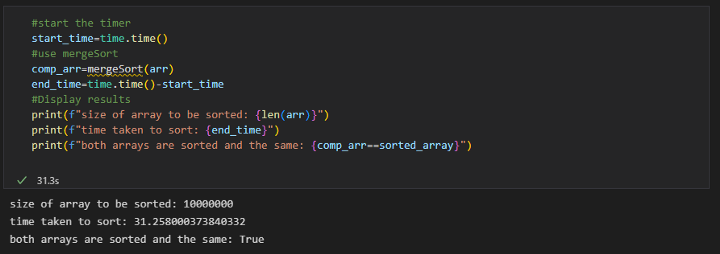
使用合并排序:
Trivial搜索
横向移动,让我从相关任务中检查第二个稍微不那么琐碎的示例。我们都知道二分查找,O(log(n))是最快的可用搜索算法,如果我们要进行多轮搜索,则值得花费O(nlog(n)的初始排序成本)对我们将要搜索的数组进行排序,以便我们可以进行二进制搜索来找到我们的目标。但是我们可以在搜索方面做得比这更好吗?事实上,我们中的许多人可能经常比这做得更好,也许在搜索术语时没有考虑到它。
假设我创建了一个字典,而不是对我们的搜索数组进行排序,我们要搜索的数组中的每个唯一元素都是字典的一个键,每个键的值是某个任意占位符。这花费了我O(n) 的时间复杂度,其中n是搜索数组的大小。现在,对于每一轮搜索,我都可以尝试在字典中找到与我的目标值匹配的键。每次我搜索时都会产生O(1)的时间复杂度(感谢散列函数),结合到O(m)来搜索我的所有目标,其中m是目标的数量。
使用其中一种经典的排序算法 + 二分查找的最终时间复杂度为O(mlog(n) + nlog(n)),其中m是我正在执行的搜索次数,n是要搜索的数组的大小 并添加第二个nlog(n)以说明排序步骤。使用字典的时间复杂度是max(O(n), O(m))。换句话说,我们将报告时间复杂度,具体取决于哪个更大——因此将主导时间要求的部分——我们变成搜索字典的数组的大小 ( n ) 或要进行的搜索次数(米)。
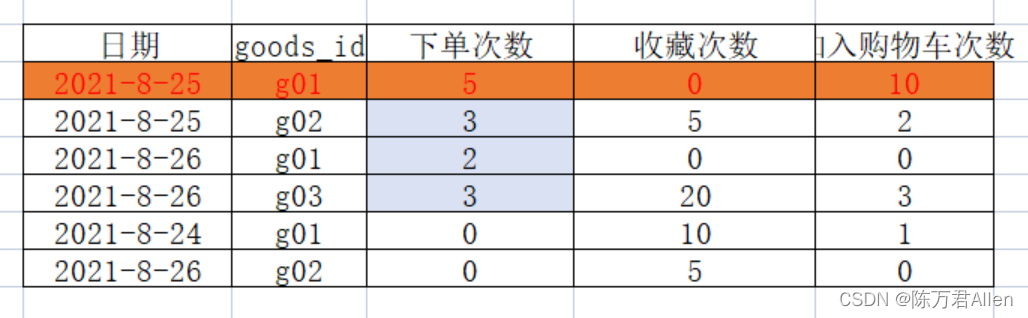
下面是这两种方法在 1000 万个元素的数组上的代码逻辑和结果的屏幕截图,其中搜索了 1000 个目标。
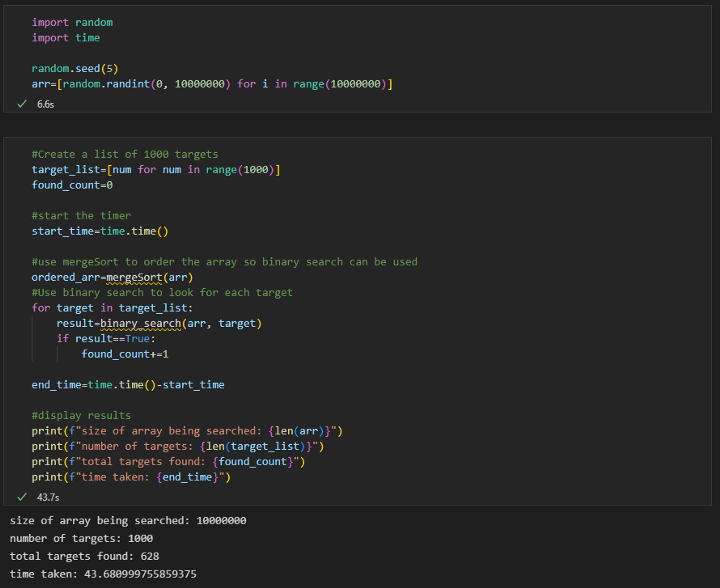
使用 mergeSort + 二分查找:
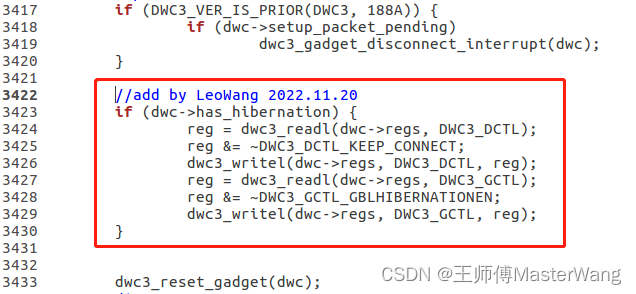
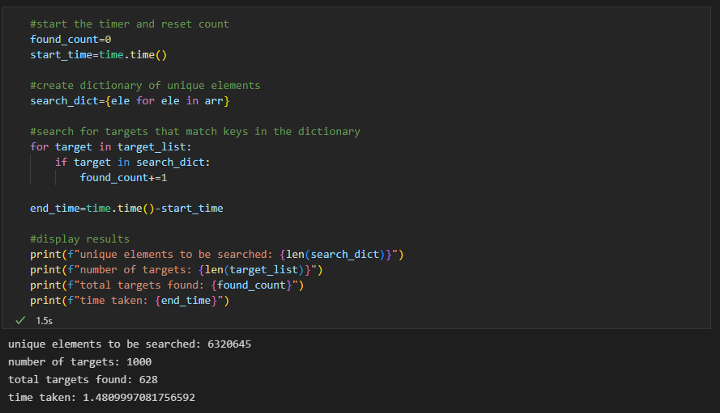
使用哈希表:
为了记录,天真地检查搜索数组中的每个元素以查找 1000 个目标中的每一个都比任何一种方法都花费了更长的时间:

讨论
这两个例子都是微不足道的,因为从表面上看,它们几乎没有能力扩展到更复杂的情况。与第一个示例一样,我们要排序的数据通常具有两个以上的值。关于第二个示例,我们需要搜索的数据类型可能是多层次的,并且不容易将其转储到字典中,或者这样做所需的准备工作将比经过验证的方法更昂贵。
但是,这些示例确实表明排序时可能比 O( nlog(n))做得更好。如果条件合适,我们可以做O(n)。同样,在搜索特定目标时,我们可以做得比 O( log(n))更好。如果我们要进行多轮搜索,最初设置一个字典可以让我们在O(1)时间内搜索单个目标。
那么问题就变成了,而不是希望在我们的数据环境中出现正确的条件,我们能否(可靠地)为(一定数量的)非平凡任务创造这些条件(至少在一定时间内)?
推荐书单
《Pandas1.x实例精解》

本书详细阐述了与Pandas相关的基本解决方案,主要包括Pandas基础,DataFrame基本操作,创建和保留DataFrame,开始数据分析,探索性数据分析,选择数据子集,过滤行,对齐索引,分组以进行聚合、过滤和转换,将数据重组为规整形式,组合Pandas对象,时间序列分析,使用Matplotlib、Pandas和Seaborn进行可视化,调试和测试等内容。此外,本书还提供了相应的示例、代码,以帮助读者进一步理解相关方案的实现过程。 本书适合作为高等院校计算机及相关专业的教材和教学参考书,也可作为相关开发人员的自学用书和参考手册。
链接:https://u.jd.com/UKjx4et
精彩回顾
《Pandas1.x实例精解》新书抢先看!
【第1篇】利用Pandas操作DataFrame的列与行
【第2篇】Pandas如何对DataFrame排序和统计
【第3篇】Pandas如何使用DataFrame方法链
【第4篇】Pandas如何比较缺失值以及转置方向?
【第5篇】DataFrame如何玩转多样性数据
【第6篇】如何进行探索性数据分析?
【第7篇】使用Pandas处理分类数据
【第8篇】使用Pandas处理连续数据
【第9篇】使用Pandas比较连续值和连续列
【第10篇】如何比较分类值以及使用Pandas分析库
长按关注《Python学研大本营》
长按二维码,加入Python读者群
扫码关注《Python学研大本营》,加入读者群,分享更多精彩