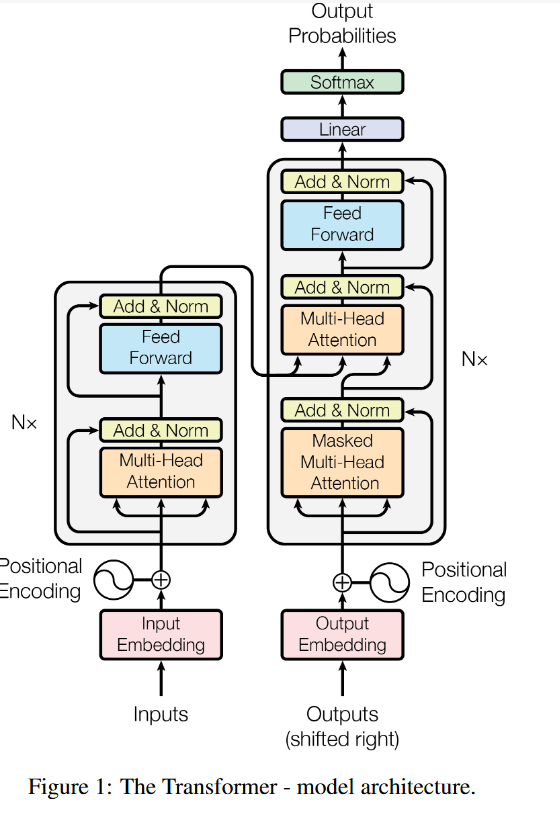
1 encoder
每个称之为一个layer,重复N次
每个里面有两个sublayer;multi-head self-attention +MLP后面使用layer normalization LayerNorm(x + Sublayer(x))
残差连接需要两个维度一致,本文采用513。
2 decoder
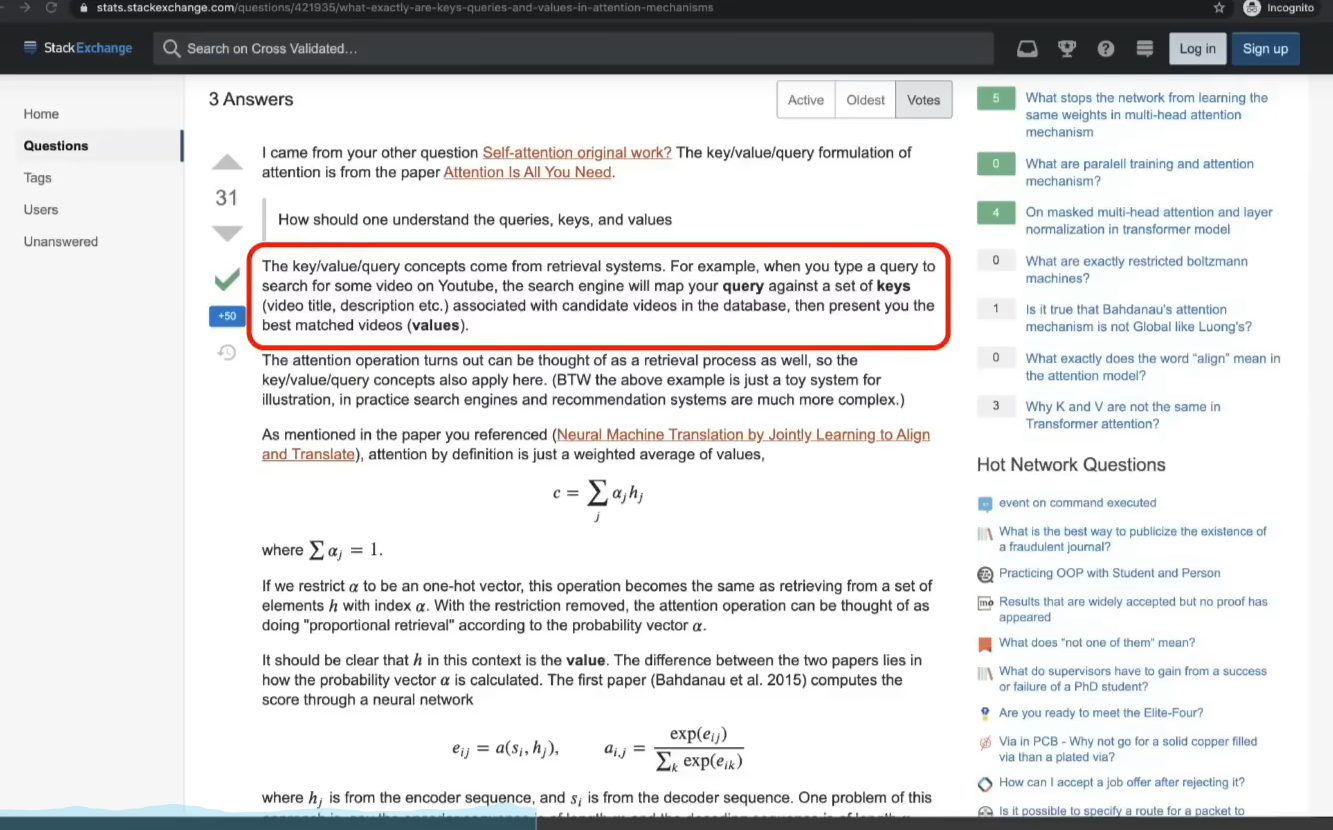
3 注意力机制
输出维度和value维度一致
两个向量做内积,表示相似度
一 原文章阅读
二 动态视图
主要内容来自3Bule1Brown
相关blog
# GPT是什么?直观解释Transformer | 深度学习第5章 【3Blue1Brown 官方双语】
GPT—Generative Pre-trained Transformer
1 总体概览
预训练:
-
模型经历了从大量数据中学习的过程
-
“预”暗示模型能针对具体任务,通过额外的训练进行微调
Transformer -
一种神经网络模型
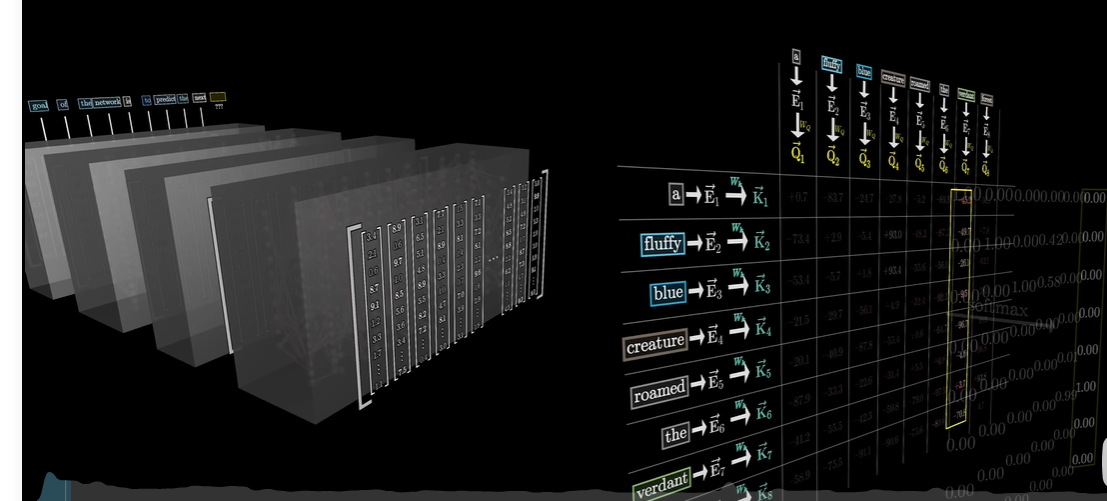
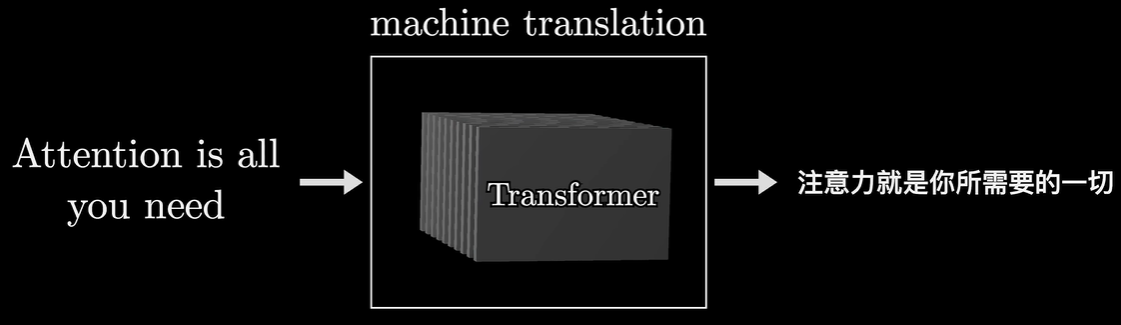
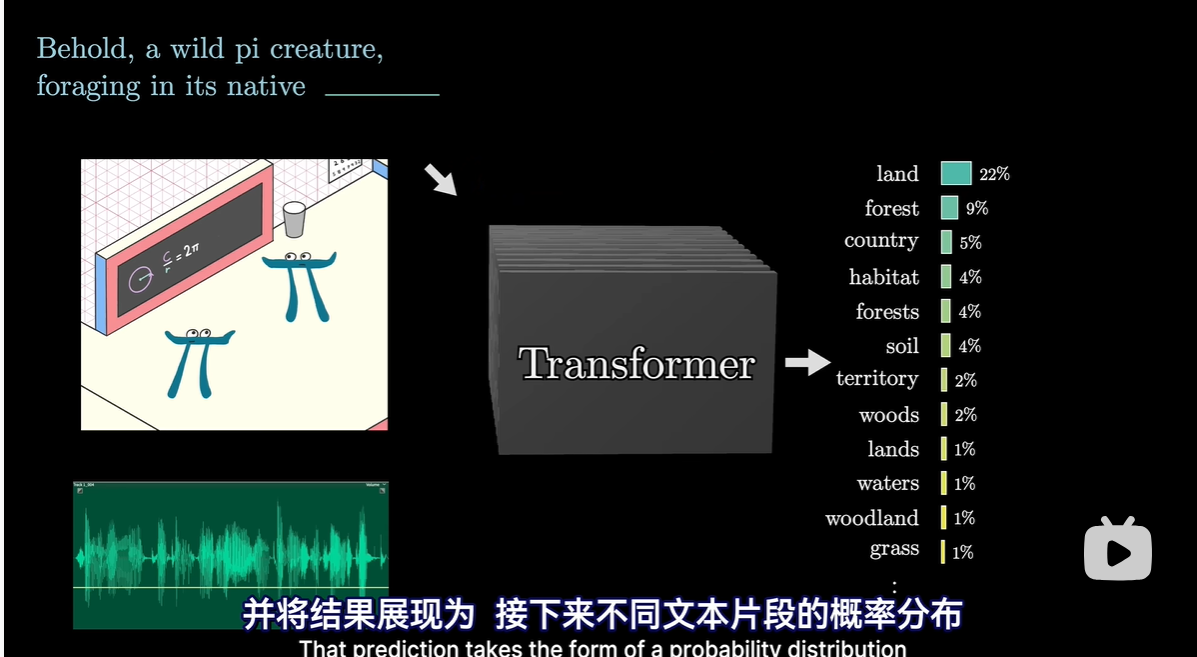

GPT–重复预测和抽样的过程
数据在GPT中的流动过程

总体概览(输入与输出): -
输入:输入内容被切分为许多小片段,称为Token

- 单词 单词片段
- 图像 小块图片
- 音频 一段声音
- 每个Token对应一个向量,即一组数字;旨在设法编码该片段含义;如果将向量看做高维空间中的坐标,那么意思相近的词,对应的向量往往相近
-
输出:

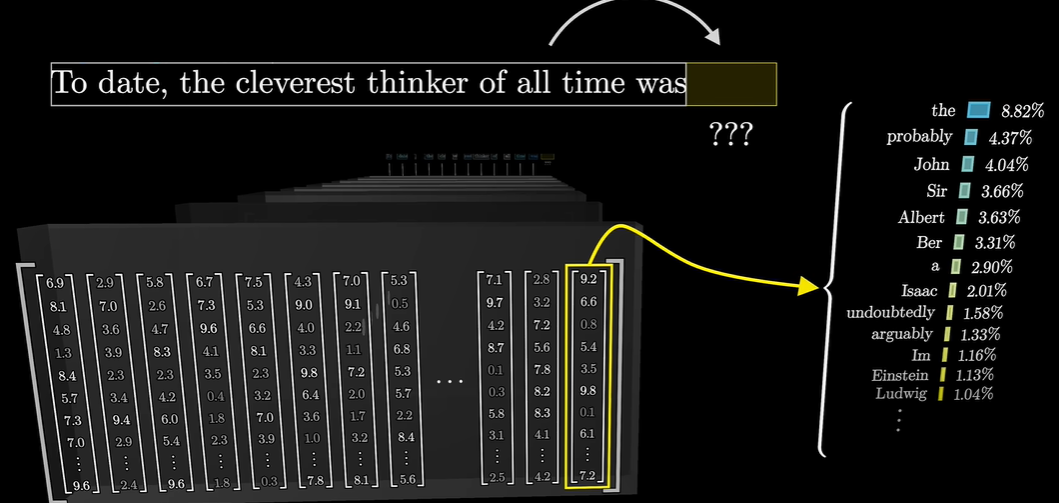
- 对最后一个向量操作,得出所有Token的概率分布
2 背景知识
本视频花时间介绍一些重要的背景知识,这些知识对于机器学习工程师来说,都应该是基本常识。
机器学习采用数据驱动、反馈到模型参数、指导模型行为
机器学习理念:不要试图在代码中,明确定义如何执行一个任务,那是AI发展初期的做法;而是去构建一个具有可调参数的灵活架构,像是旋钮和滑块;然后通过大量的实例和数据,调整各种参数值
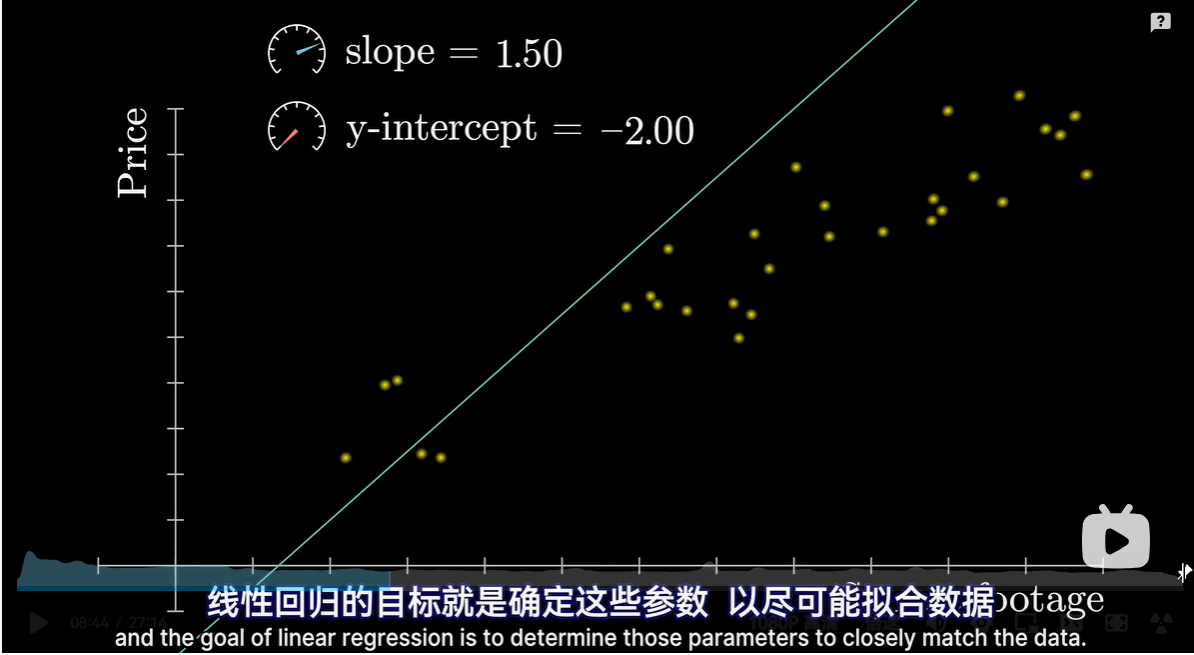

- 首先,无论构建任何模型时,输入的格式必须是实数数组

- 可以是一维数列、二维数组,或者更常见的高维数组,也就是所谓的张量(Tensor)
- 深度学习中,模型的参数称为权重
- 参数与待处理数据唯一的交互方式是通过加权和,模型中虽然有非线性函数,但他们不依赖于参数
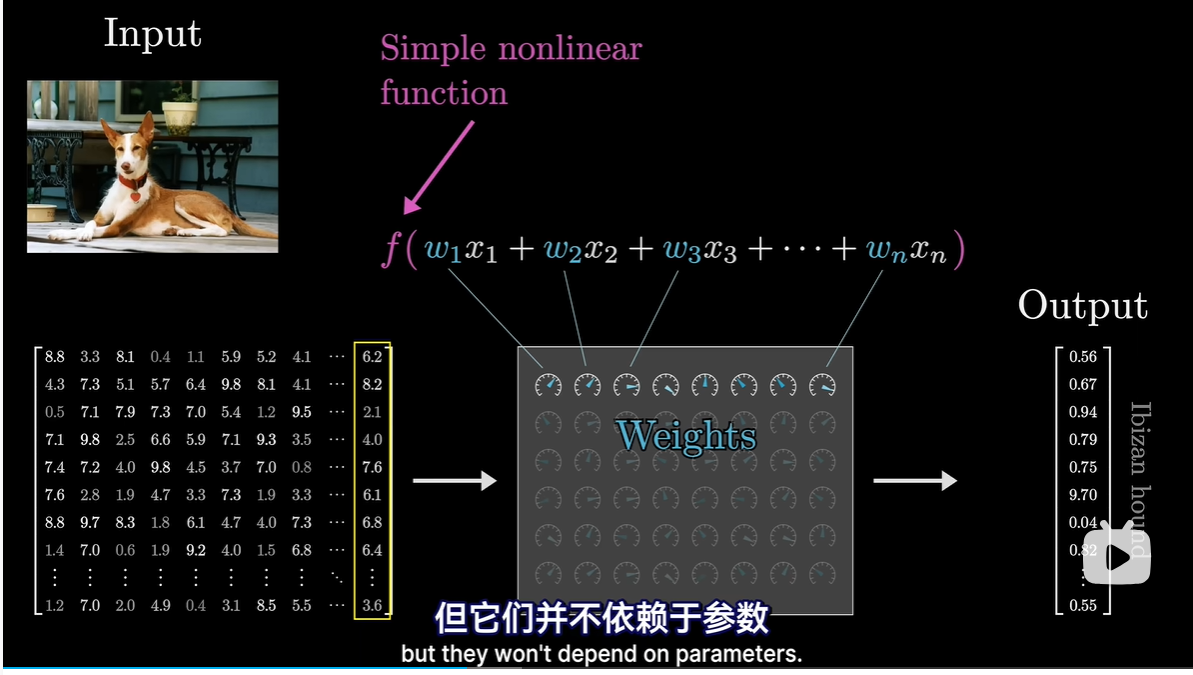
- 数学中加权和不会赤裸裸地写出来,而是打包成矩阵乘的形式,本质上是一样的

- 概念上更直观的方式是将充满可调参数的矩阵想象成能够代表待处理数据的向量进行变换的工具
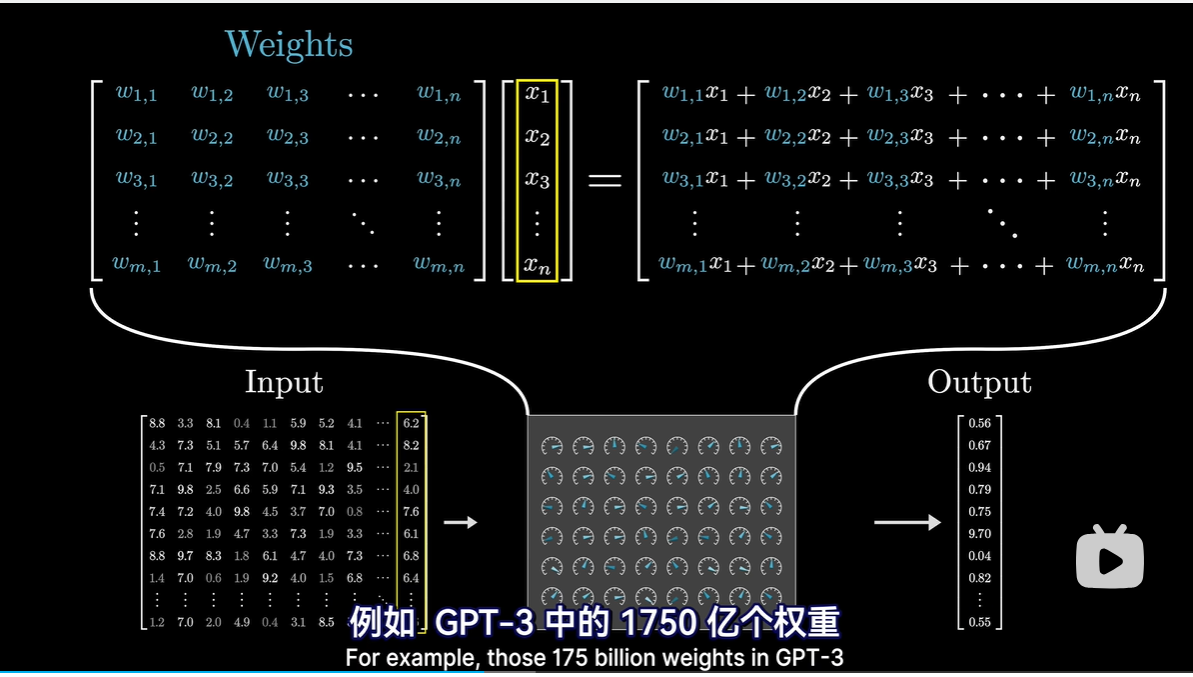
- 例如GPT-3中1750亿个参数组成近28000个矩阵,矩阵又分为8类,需要逐一了解各个类别的作用


- 权重是模型的大脑,是在训练过程中学习到的,决定模型的行为模式
1 嵌入矩阵

每个词对应一列
矩阵WE:就和其他矩阵一样,它的初始值随机,但将基于数据进行学习

为什么嵌入矩阵设置为可调参数
- 增加泛化能力:如果设置为固定的,就无法适应特定任务的需求,通过训练,embedding层可以学习到更适合当前任务的词向量表示。例如,在情感分析任务中,某些词汇的情感色彩可能会比它们的一般含义更重要,因此让embedding参数随着训练而调整可以帮助捕捉这种细微差别。
- 协同优化:在端到端的训练过程中,embedding层和其他层的参数是共同优化的。这意味着embedding层的学习可以受益于后续层的信息,反之亦然。固定embedding层将切断这种潜在的信息流,可能导致次优解
为什么嵌入矩阵设置为随机值 - 避免局部最小值:找到最优解
- 加速收敛:一些研究表明,良好的初始化可以加速训练过程中的收敛速度。例如,He初始化、Xavier/Glorot初始化等方法,都是为了在一定程度上平衡权重矩阵的方差,从而帮助模型更快地学习
- 利用上下文信息:对于嵌入层而言,随机初始化允许模型从头开始学习词汇或其他单元的最佳表示,而不是依赖于任何预先存在的假设。这对于训练一个从零开始的新模型尤为重要。
-
词嵌入
从几何角度理解向量,并将他们视为高维空间的点
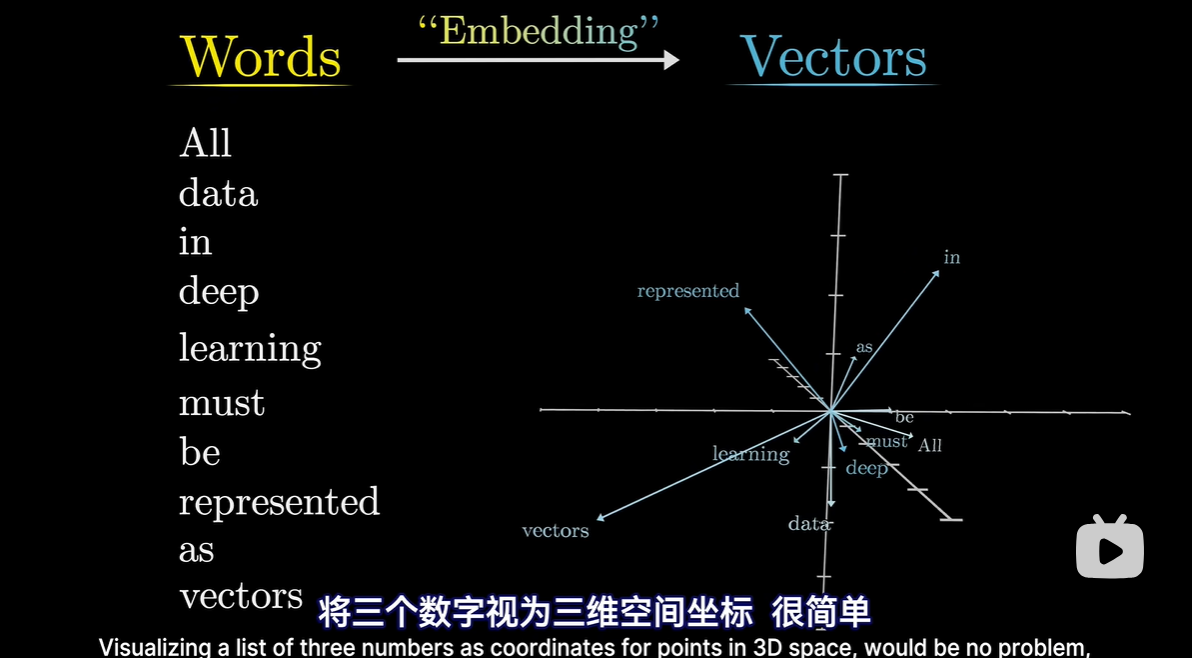
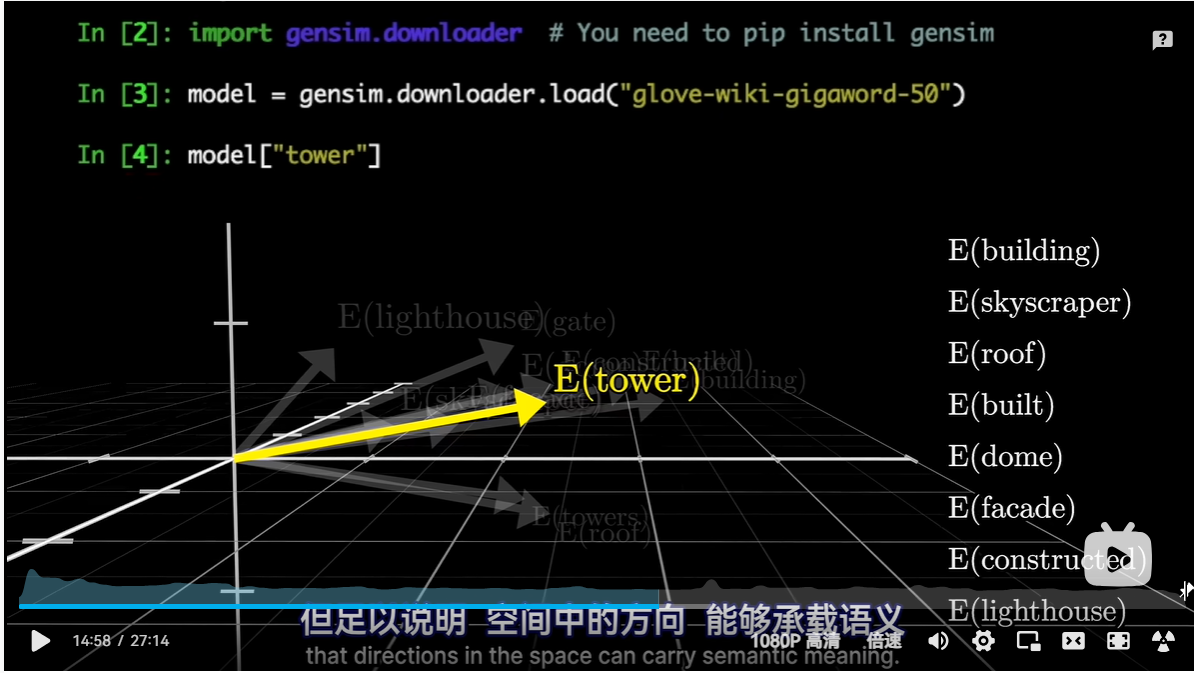
import gensim.downloader model=gensim.downloader.Load("glove-wiki-gigaword-50") model["tower"]其中,
glove-wiki-gigaword-50基于2B条推文、27B个令牌、120万个未加套的vocab的预训练得到的向量。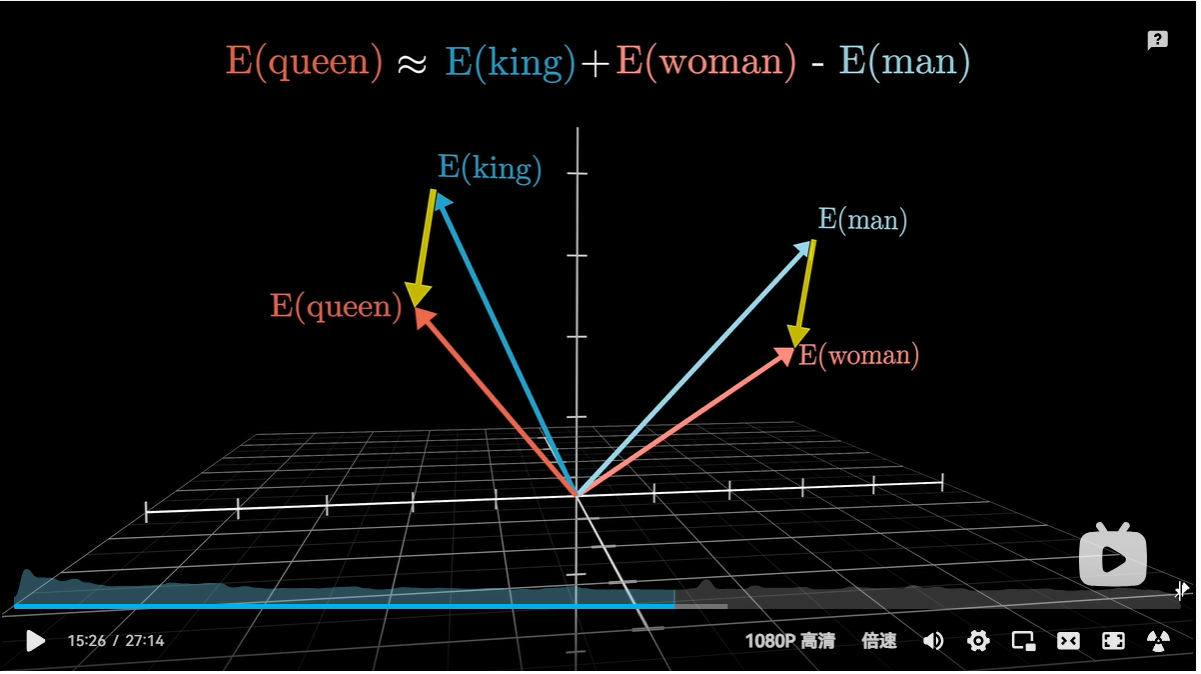
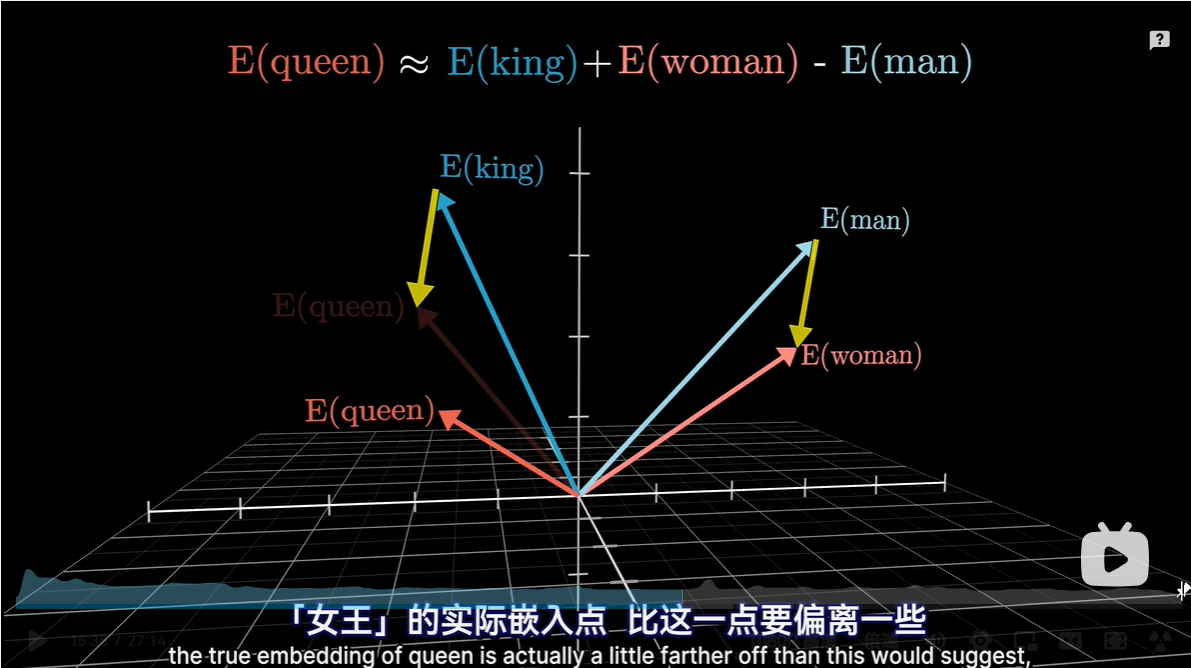
用空间中一个方向编码性别信息,更有优势
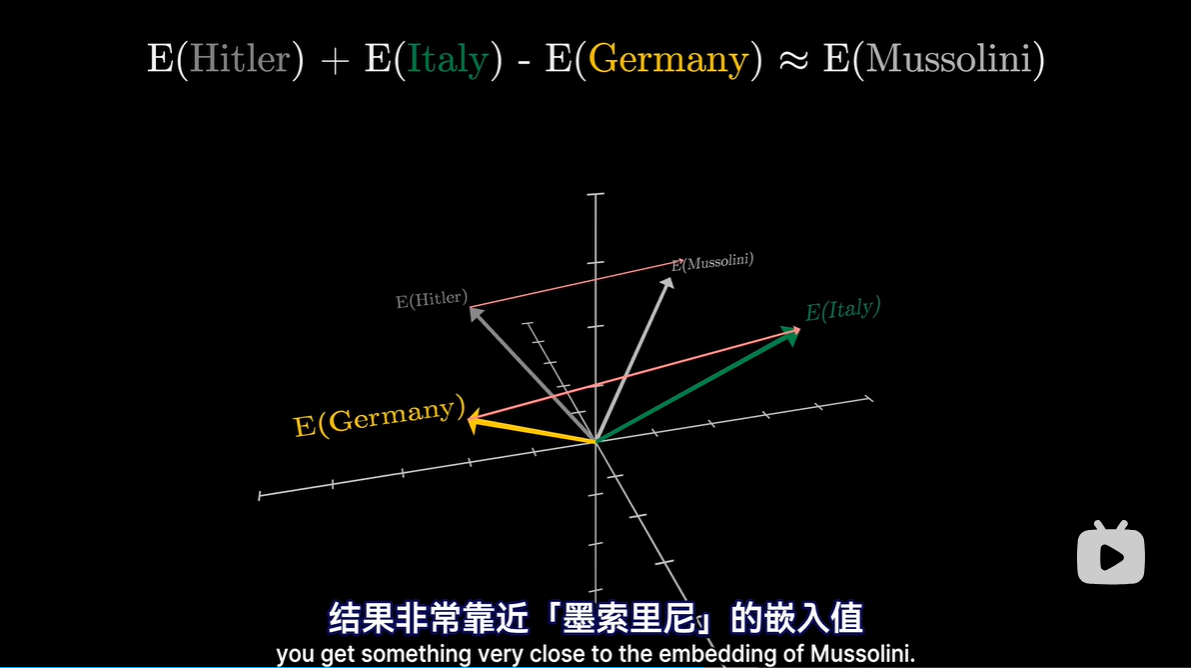
- 点积
- 代数上
所有对应分量相乘然后加和
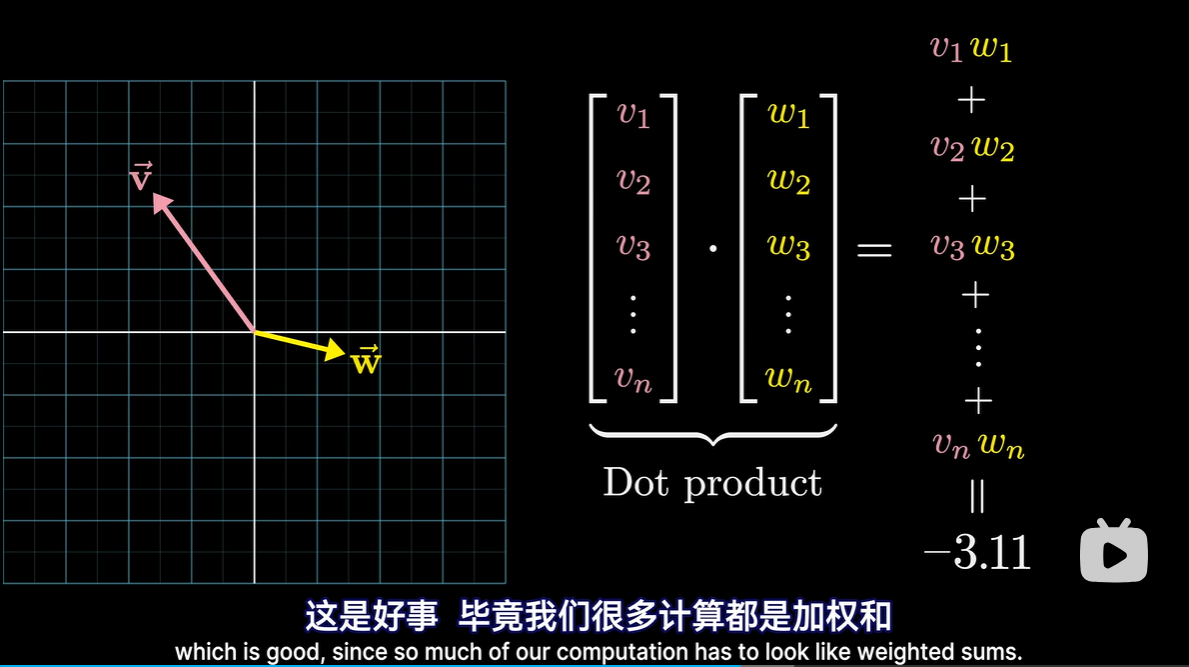
- 几何
- 向量的方向相近,则点积为正
- 方向垂直,点积为0
- 向量指向相反,点积为负
- 举例:cats-cat表示可能表示空间中复数的方向,其与名称复数的点积数据值大于与名词单数的点积;这表示它们在方向上更加对齐
- 代数上
- 词嵌入的具体方式也是从数据中学来的
- 嵌入矩阵一列对应一个单词,是模型中的第一组权重

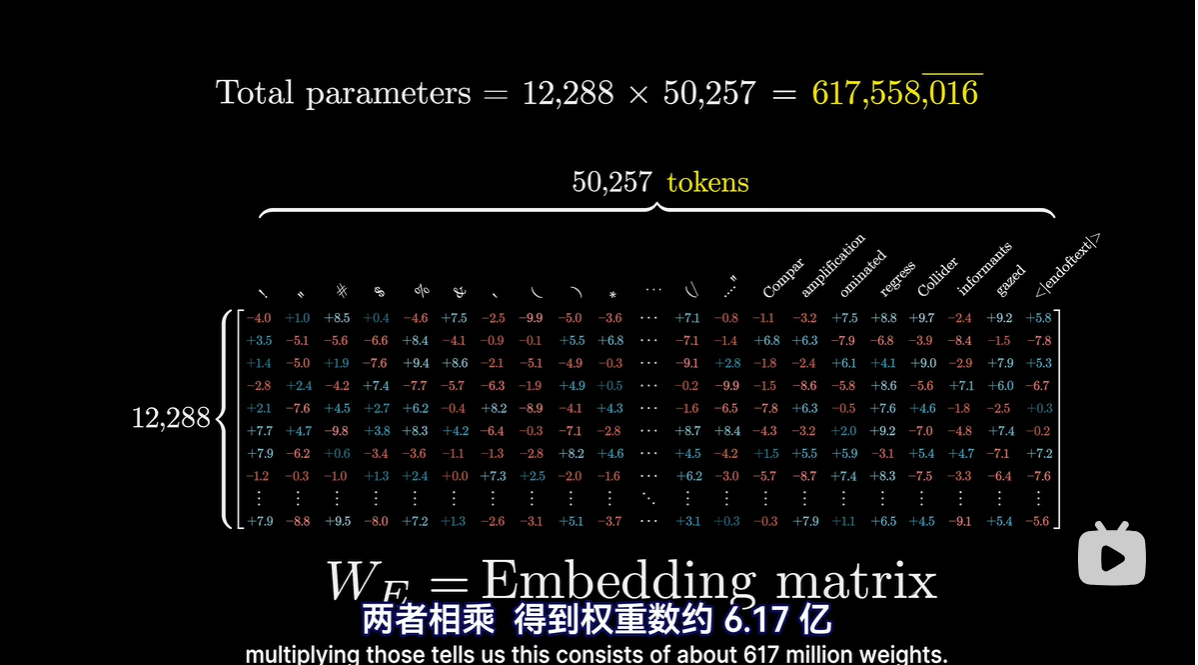
- 一开始,每个向量都是从嵌入矩阵中拉出来,最开始每个向量只能编码单个单词的含义,没有上下文含义
- embedding作用
- 词表包含token数量:50257
- 每个token维度:12288
- 点积
- Attention 网络
- 主要目标
- 使向量获得比每个词更丰富更具体的含义
- 上下文长度
- 一次只能处理特定数量的向量,称为上下文长度
- GPT3上下文长度为2048,流经网络的数据有2048列,每列12288维


- 上下文长度限制Transformer预测下个词时,能结合的文本量
- 主要目标
- 最终阶段的处理
- 目标输出:下一个可能Token的概率分布
- 过程
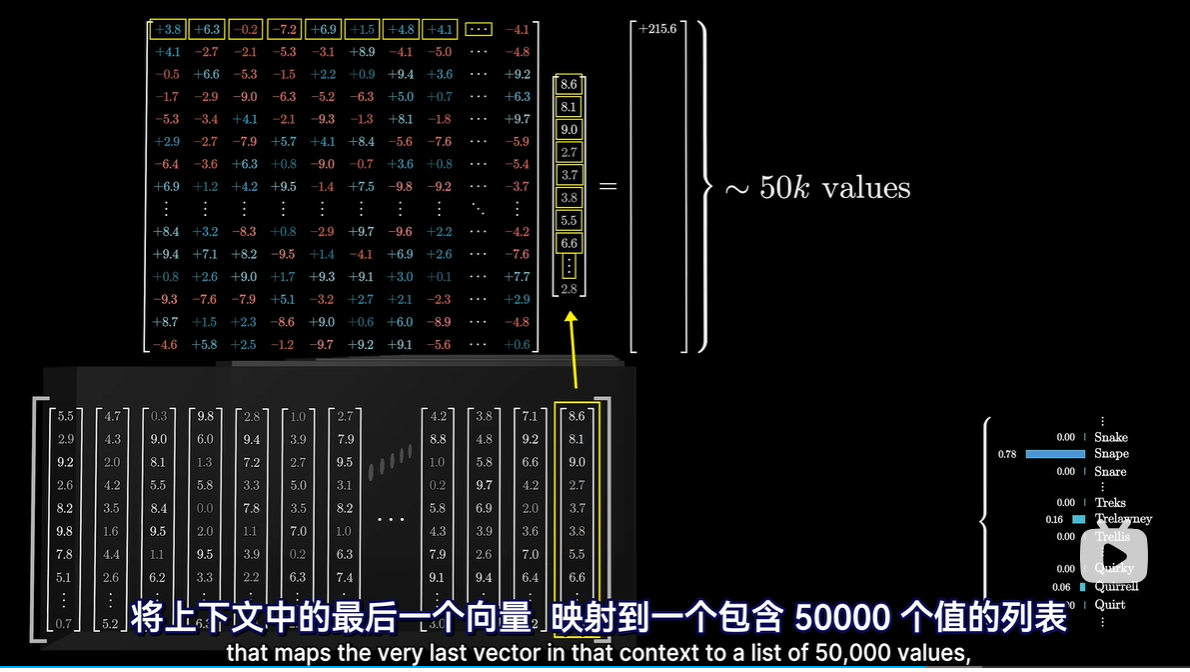
- 每一行对应词库中的一个token
- Softmax函数将其归一化为概率分布

- 为什么只用最后一个嵌入做预测
- 训练过程中效率更高的方法是利用最终层的每一个向量,同时对紧随者这个向量的词进行预测
2 解嵌入矩阵Wu
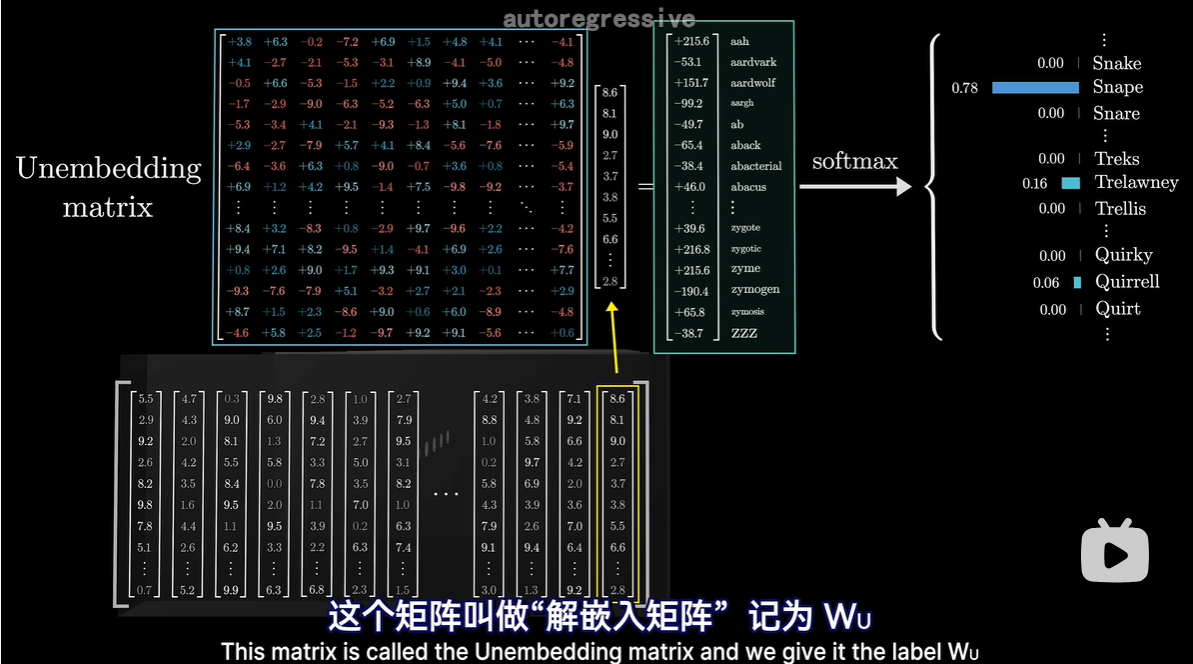
- 和其他权重矩阵一样,初始值随机,但在训练过程中学习;
- 他的每一行对应词汇库中的每一个词,每一列对应一个嵌入维度
- 与嵌入矩阵相似,只是行列对调
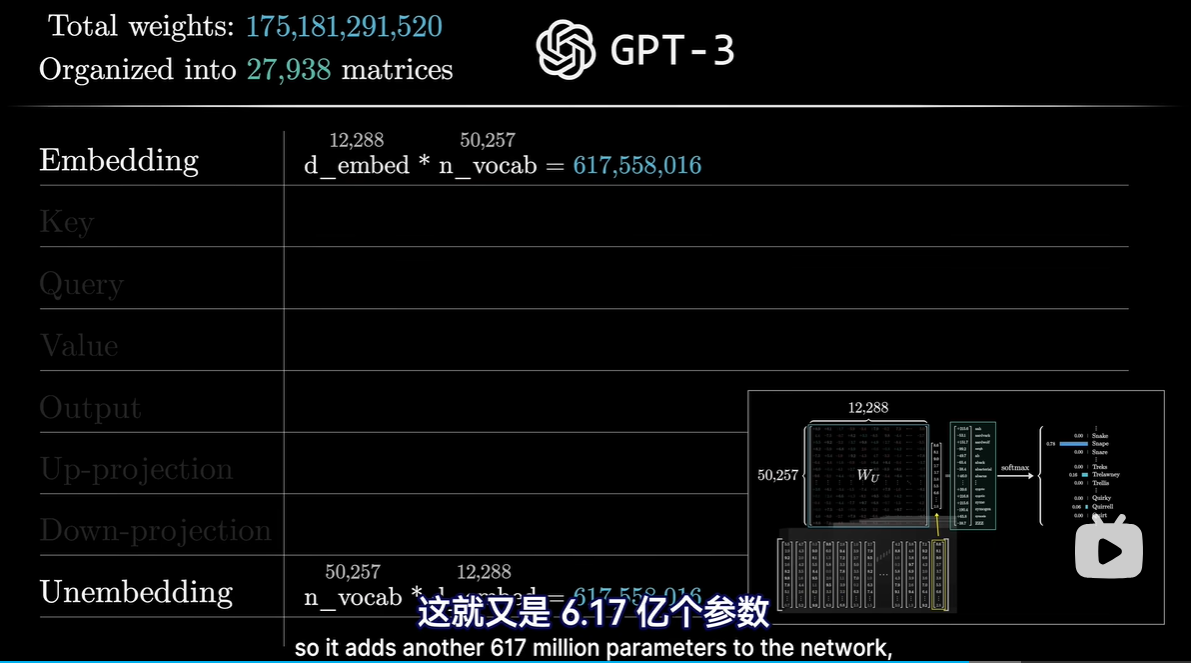
transformer中嵌入矩阵和解嵌入矩阵是同一个矩阵吗
在Transformer模型中,嵌入矩阵(embedding matrix)和解嵌入矩阵(通常称为投影矩阵或解码矩阵)并不一定是同一个矩阵。具体取决于模型的设计和实现方式。- 嵌入矩阵:这是将输入的离散符号(如词汇索引)映射到连续向量空间的一个矩阵。每个词汇对应一个特定的行向量,这些行向量构成了嵌入矩阵。
- 解嵌入矩阵:在一些模型中,特别是在分类任务中,输出层可能会有一个额外的矩阵来将Transformer的最后一层的输出映射回原始词汇空间或其他标签空间。这个矩阵有时被称为投影矩阵或解码矩阵。
在许多情况下,特别是在机器翻译任务中,输入词汇表和输出词汇表是相同的。这时,为了简化模型并共享参数,可以使用同一个矩阵作为嵌入矩阵和解嵌入矩阵。这种方法的一个好处是可以减少模型参数的数量,从而减少过拟合的风险,并且在实践中也被证明可以提高性能。
在Transformer的原始论文中提到,对于机器翻译任务,如果输入和输出共享相同的词汇表,则可以在输出层使用与输入嵌入相同的权重矩阵。这意味着在训练过程中,这个矩阵既用于嵌入输入序列,又用于将最终的模型输出投影回词汇空间。这样做可以通过共享输入和输出之间的信息来进一步提升模型性能。
然而,并不是所有的实现都会这样做。在一些任务中,输入和输出词汇表可能不同,或者即使相同,也可能选择不共享嵌入矩阵以避免潜在的问题。因此,是否使用同一个矩阵取决于具体的应用场景和设计选择。
- Softmax函数
- 基本想法
- 若想将一串数字作为概率分布,比如所有可能得下一个词的概率分布,那么每一值必须介于0-1,并且总和为1
- 给函数增加一些趣味性
- 给指数加个分母,常量T,被称为温度
- 当T较大时,会给低值赋予更多的权重,使得分布更均匀
- T=0,所有权重给最大值
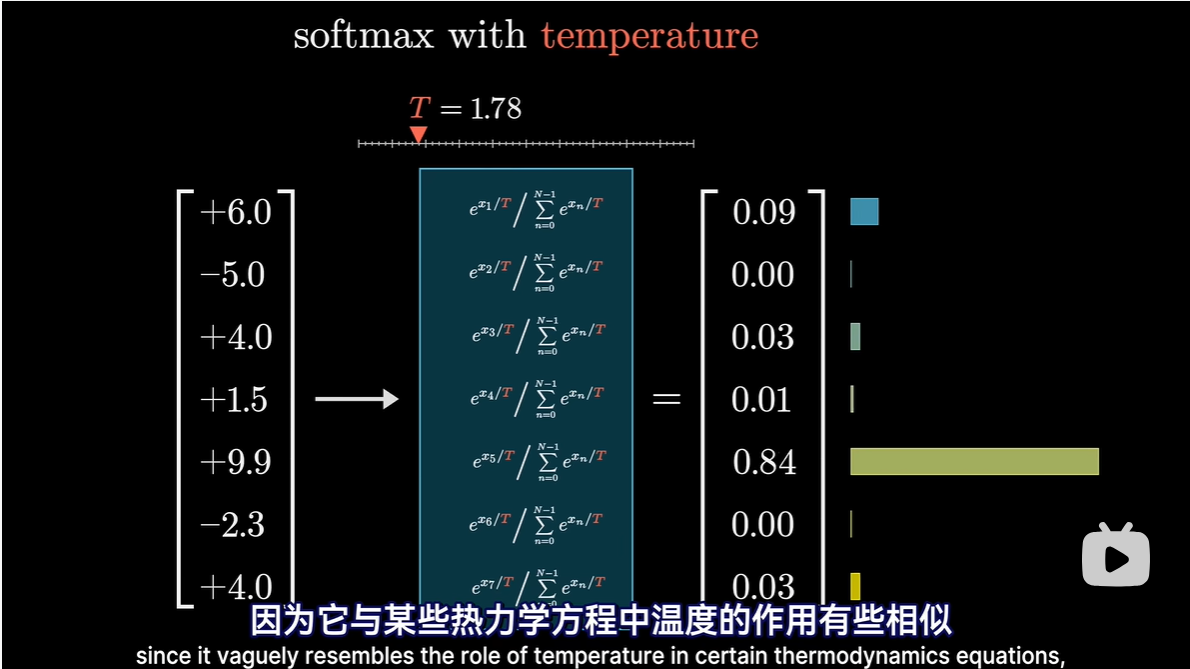
- 术语 logits
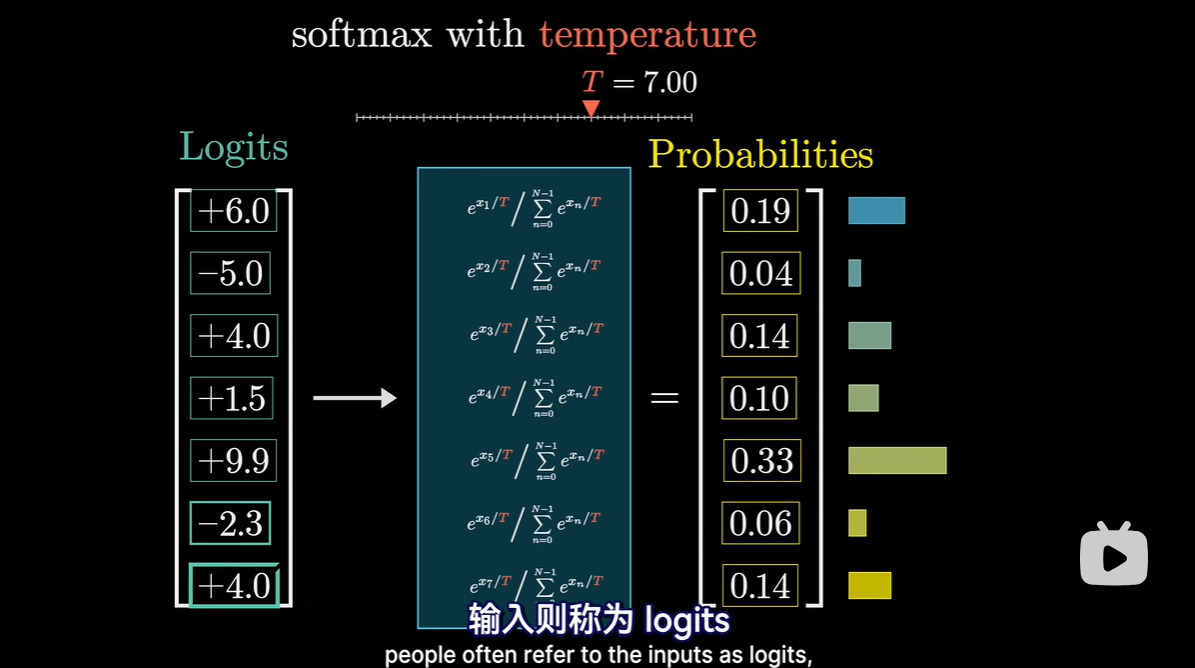
- 基本想法
小节
- karate kid wax-on-wax-off式基础训练
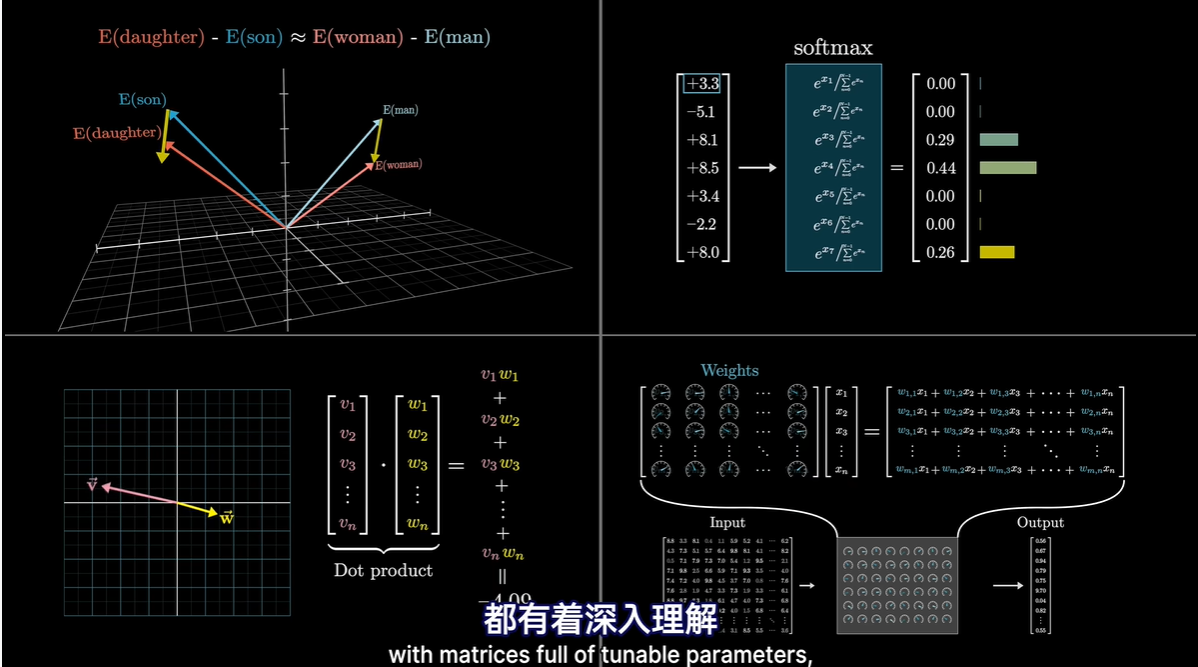
3 Attention
-
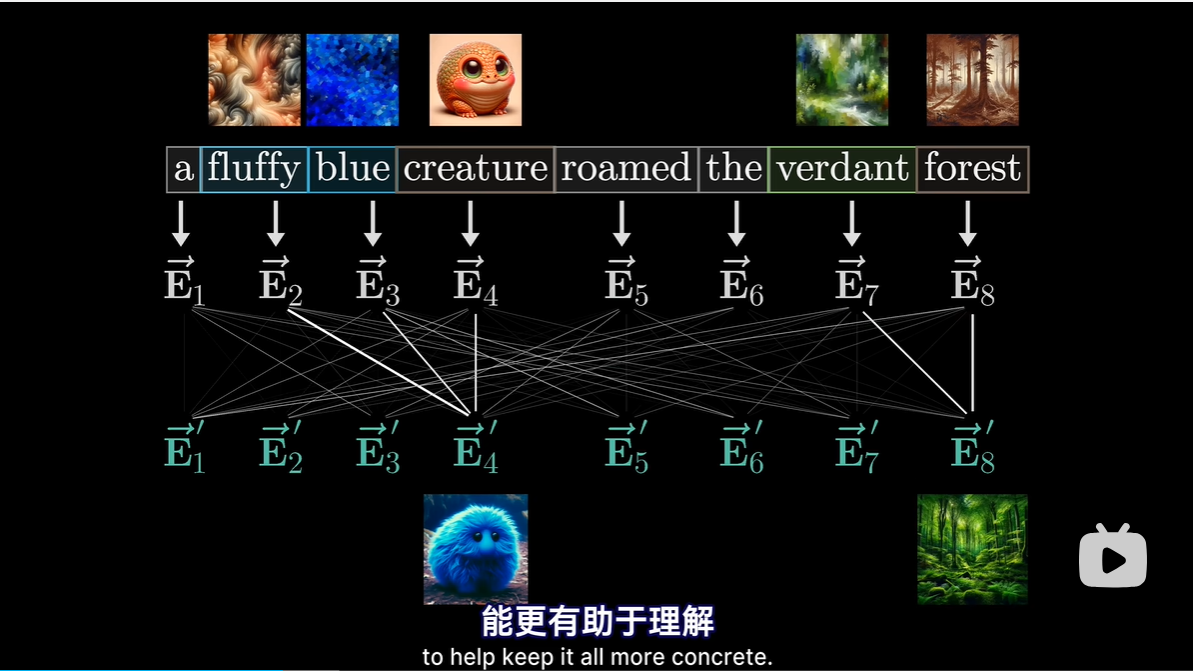
-
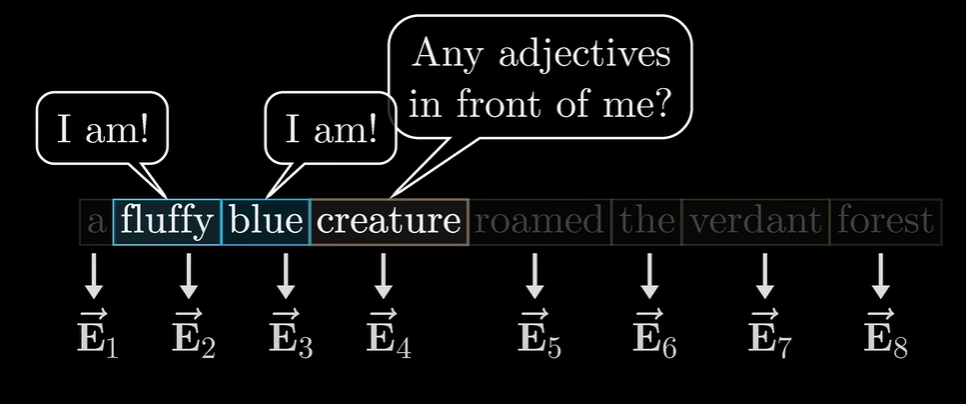
-
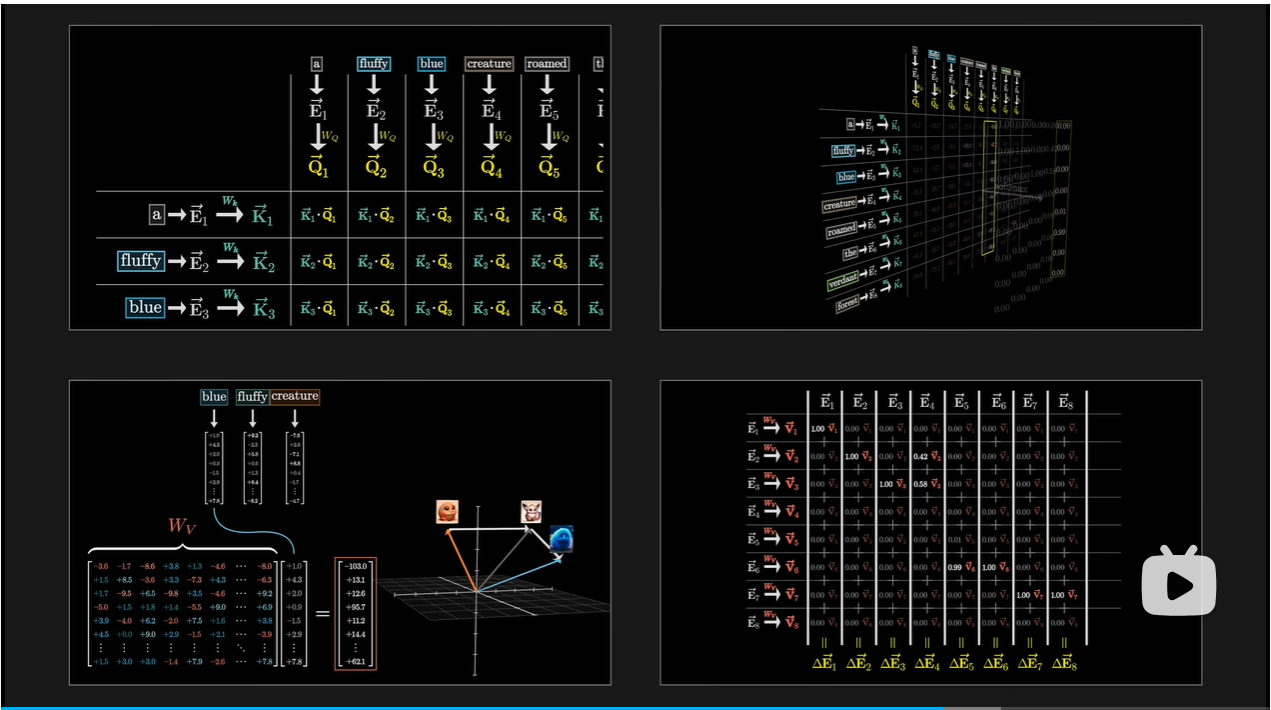
提问被编码为另一个向量,也就是另一组数字
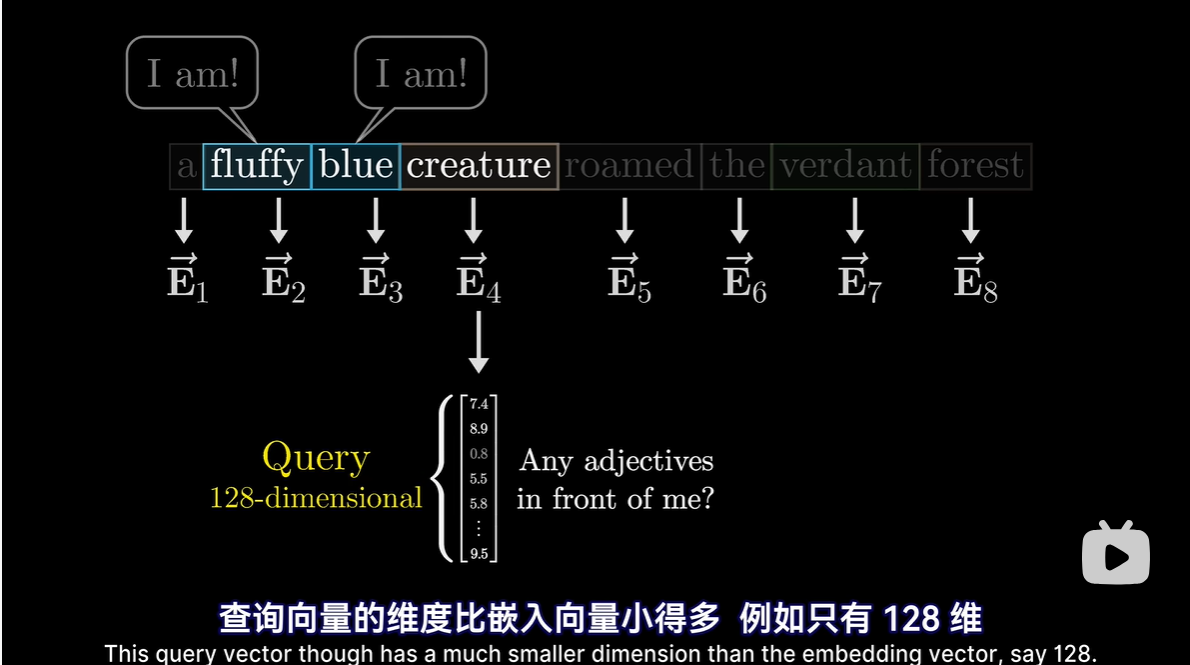
-
Query矩阵:要计算查询向量,先取一个矩阵Wq,然后乘以嵌入向量
-
Wq内部数值是模型的参数,具体行为模式从数据中学得
-
可以理解为将嵌入空间中某个方向映射为较小的查询空间的方向,用向量来编码“寻找前置形容词”的概念
-
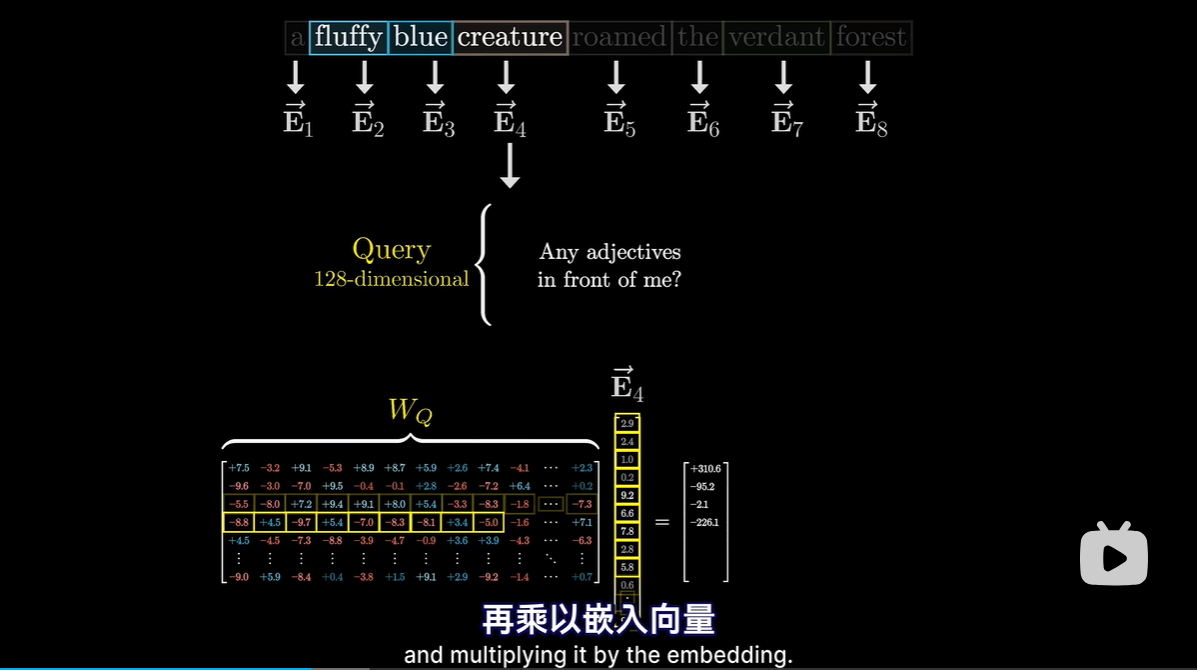
-
每个token算出一个查询向量
-

-
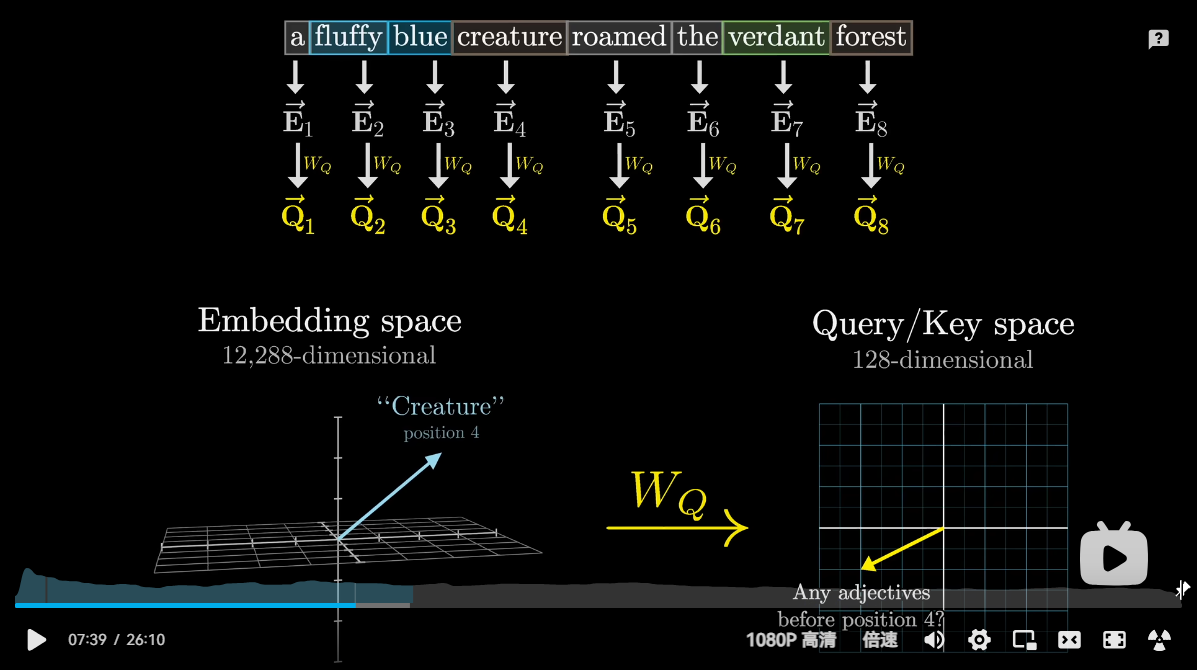
-
Q(Query)矩阵:查询矩阵代表了模型想要查询的信息。它是由输入序列的嵌入经过一个线性变换得到的。查询向量反映了输入序列中的每个位置想要获取的信息类型。
-
Key矩阵
-
K(Key)矩阵:键矩阵包含的是每个位置处的信息摘要,它同样由输入序列的嵌入经过另一个线性变换得到。键向量用于匹配查询向量,以确定哪些信息片段应该被关注。
-
从概念上可以把Key视作想要回答的Query
-
Key矩阵也填满可调参数,类似Q矩阵,将嵌入向量映射到相同的低为维度空间
-

-
当键和查询方向相对齐时,认为它们相匹配
-
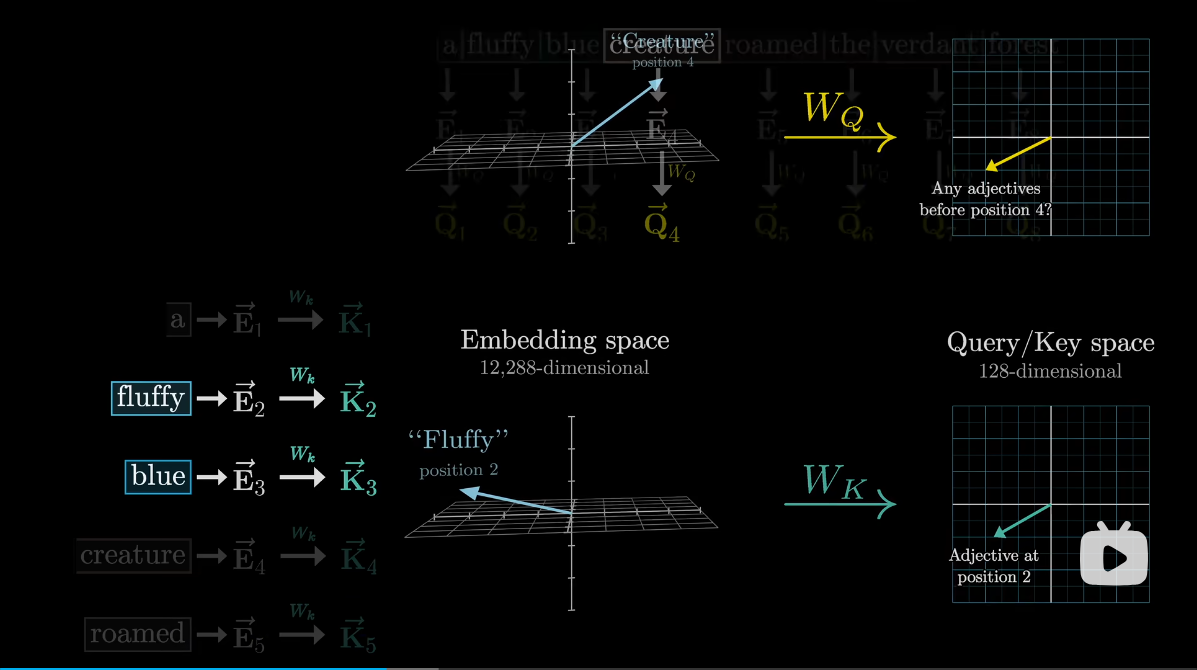
-
用点积表示相关量
-

-
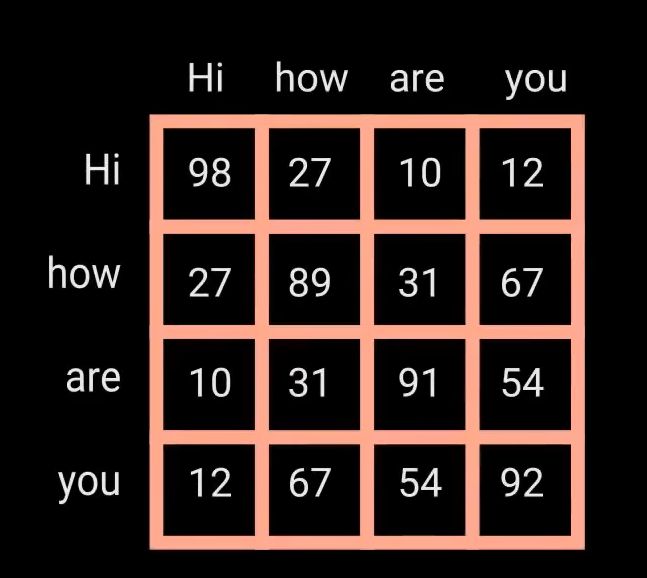
分数表示每个词与更新其他词的含义有多相关
-
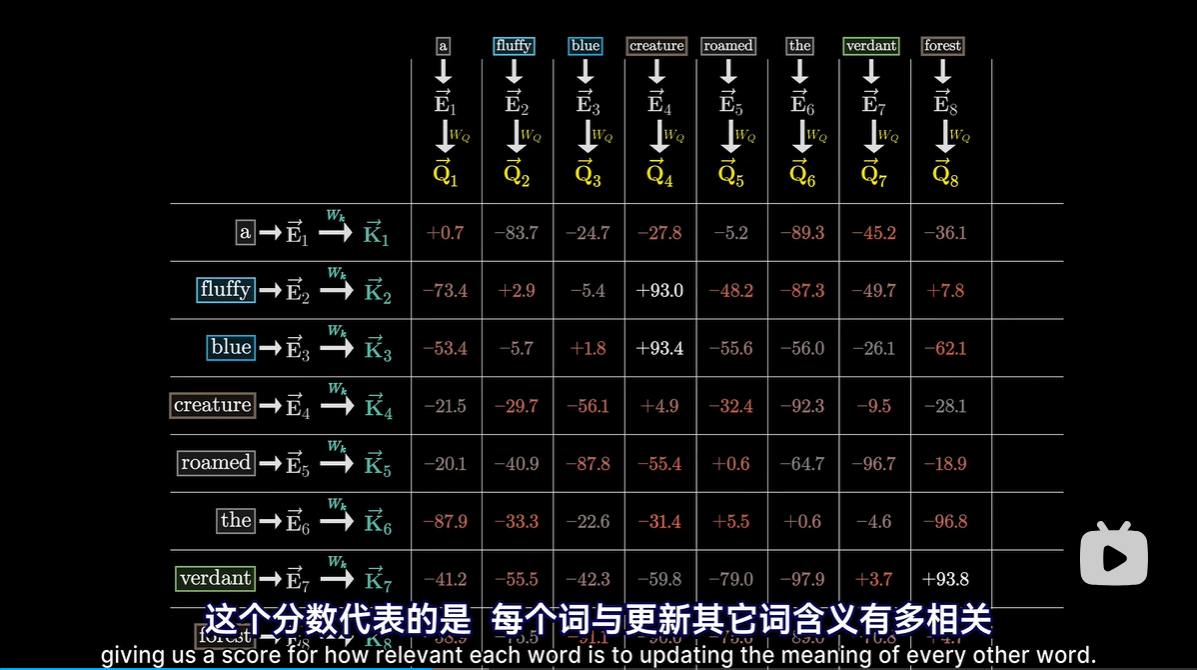
-
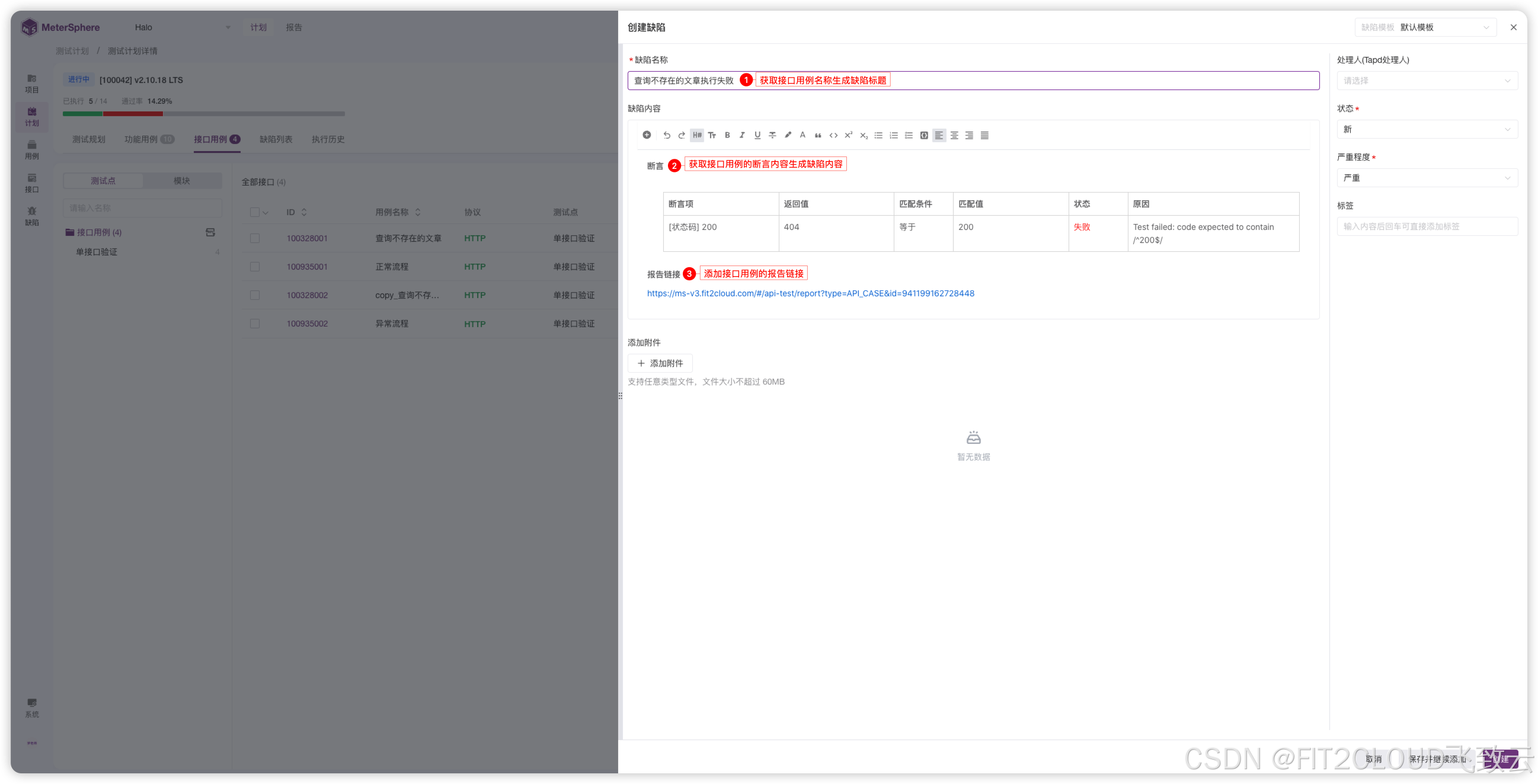
分数的用法就是对每一列加权求和,权重是相关性
-
对每一列使用Softmax函数归一化,用归一化的值填入网络,里面的值称为Attention Pattern
-
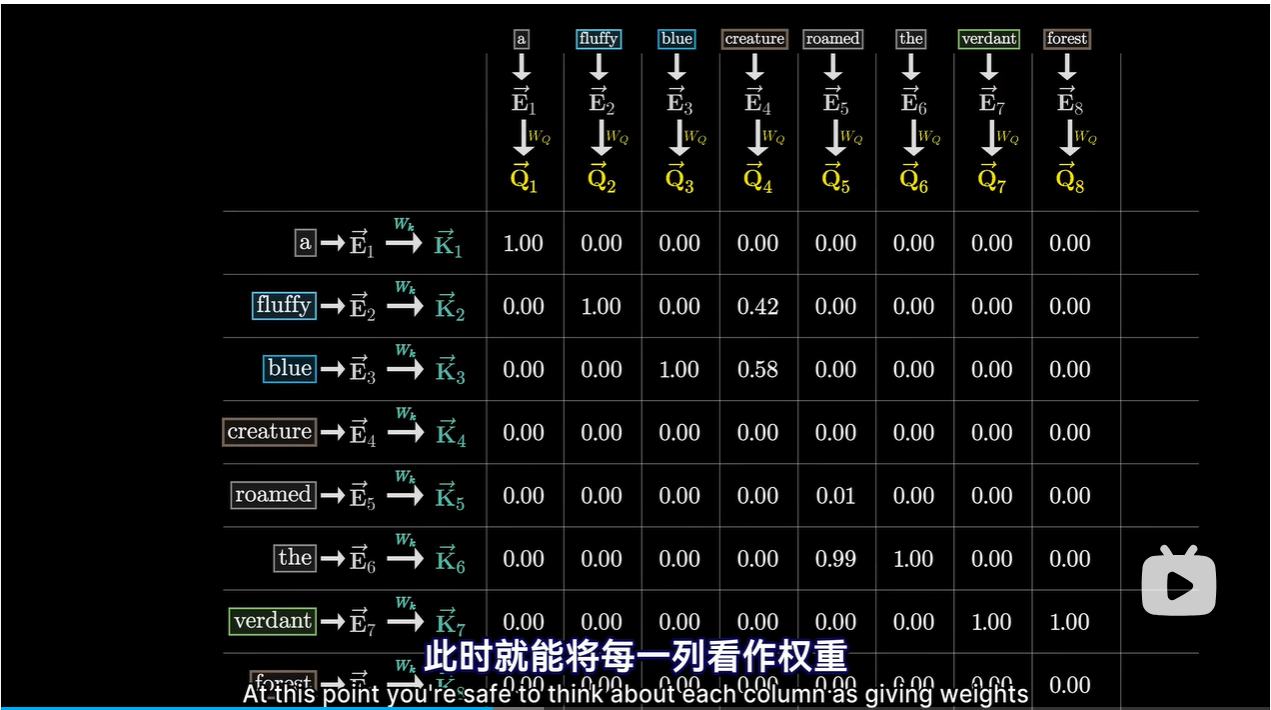
-

-
掩码:防止后面的token影响前面的token
-
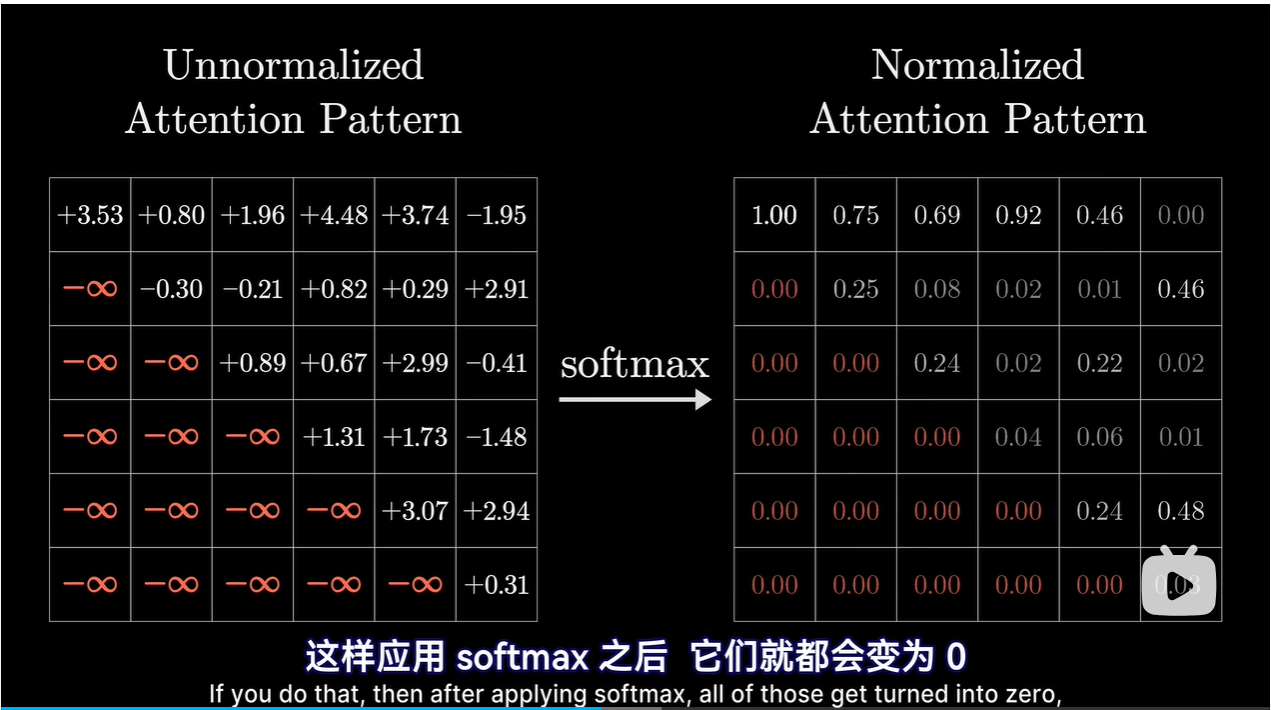
-
其大小等于上下文长度的平方
-

-
值矩阵
-
V(Value)矩阵:值矩阵包含了实际的信息内容,它也是通过输入嵌入经过第三个线性变换获得的。一旦确定了哪些信息片段需要关注,值向量就会被用来构建最终的输出。
-

-
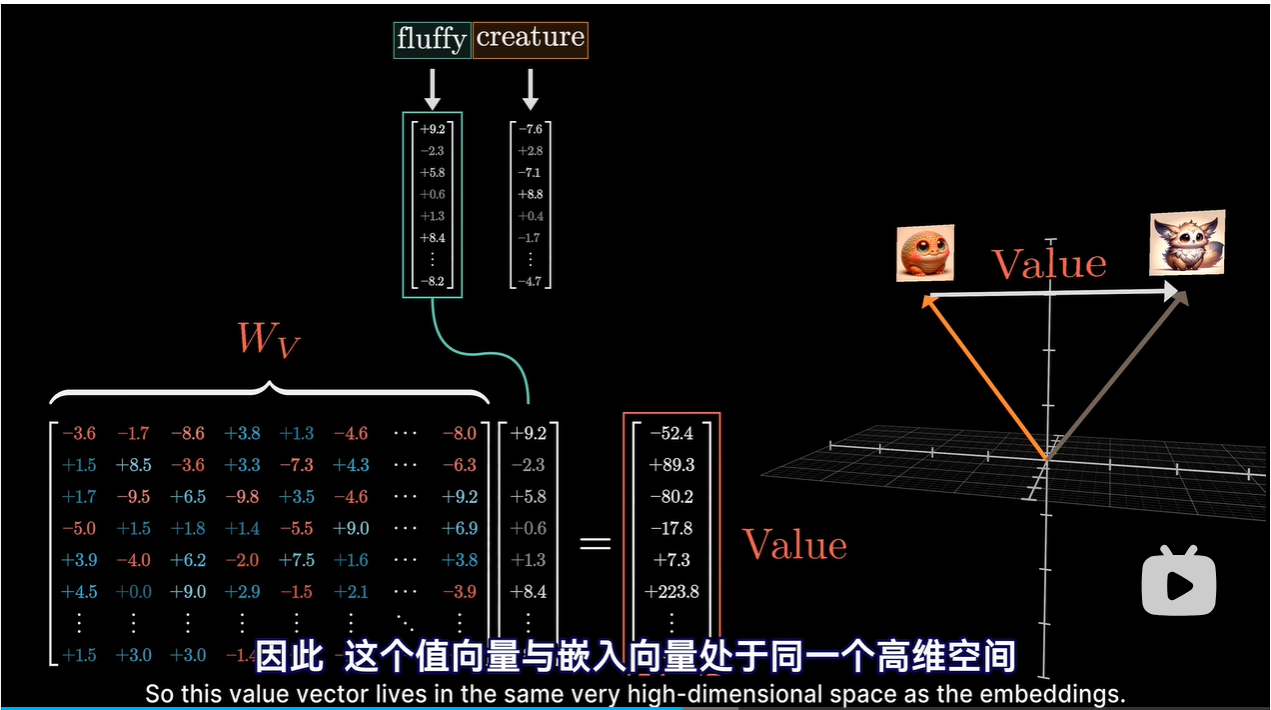
-
值向量可以想象成与对应的Key向量相关联
-
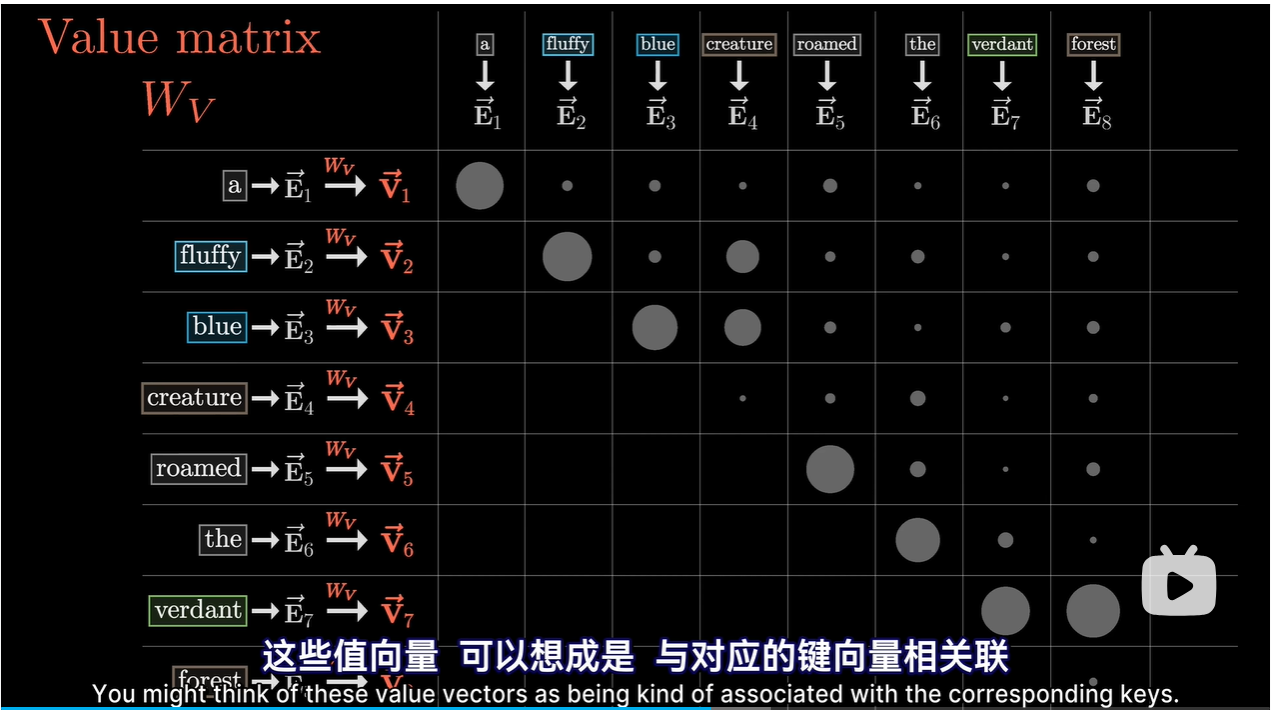
-
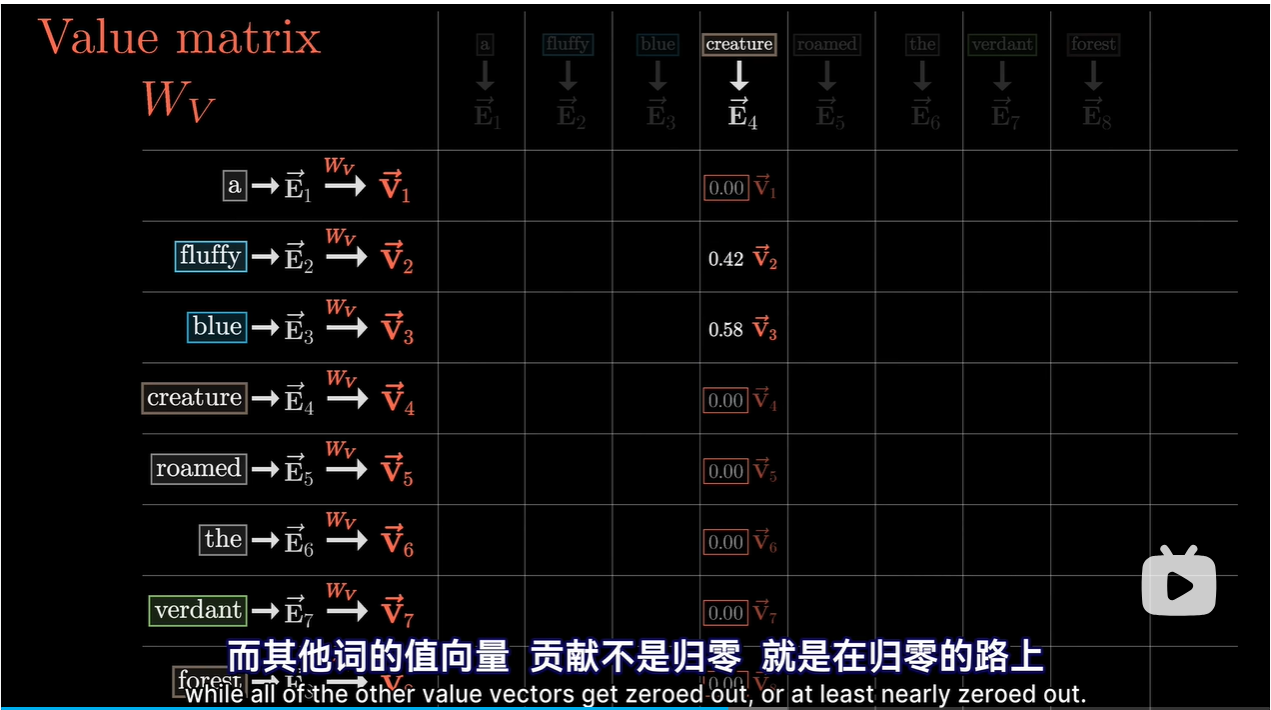
-
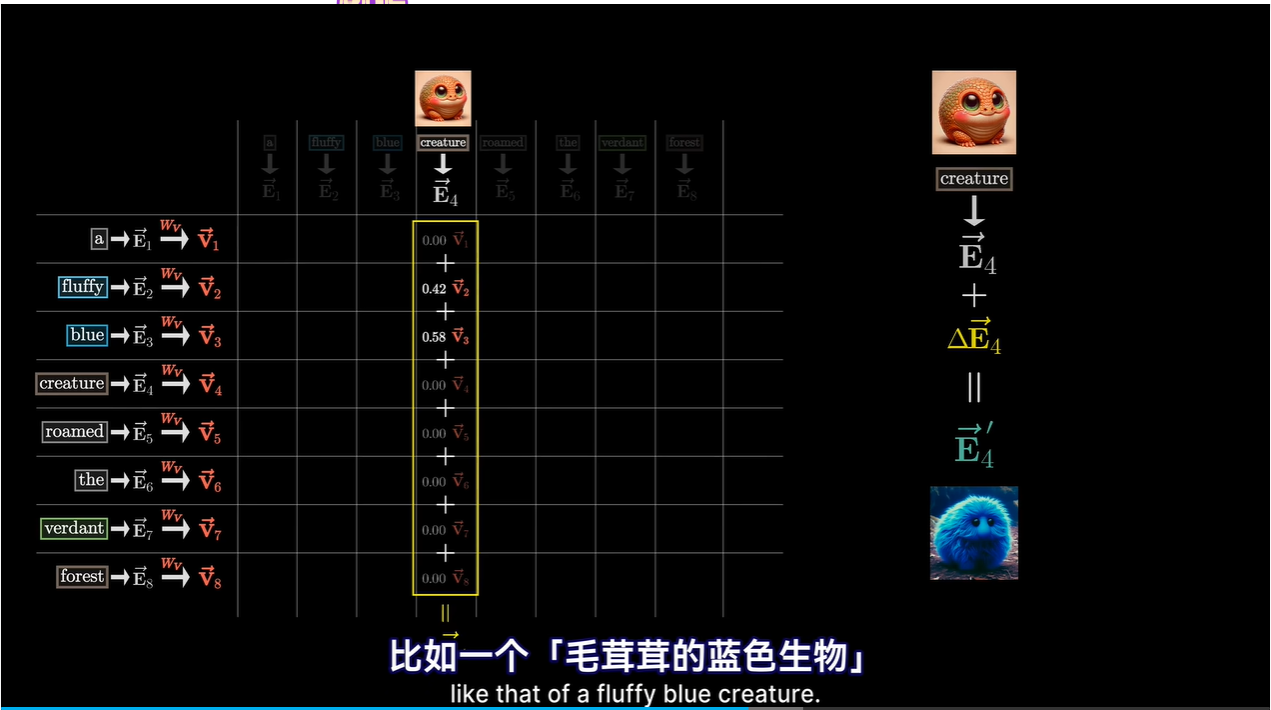
-
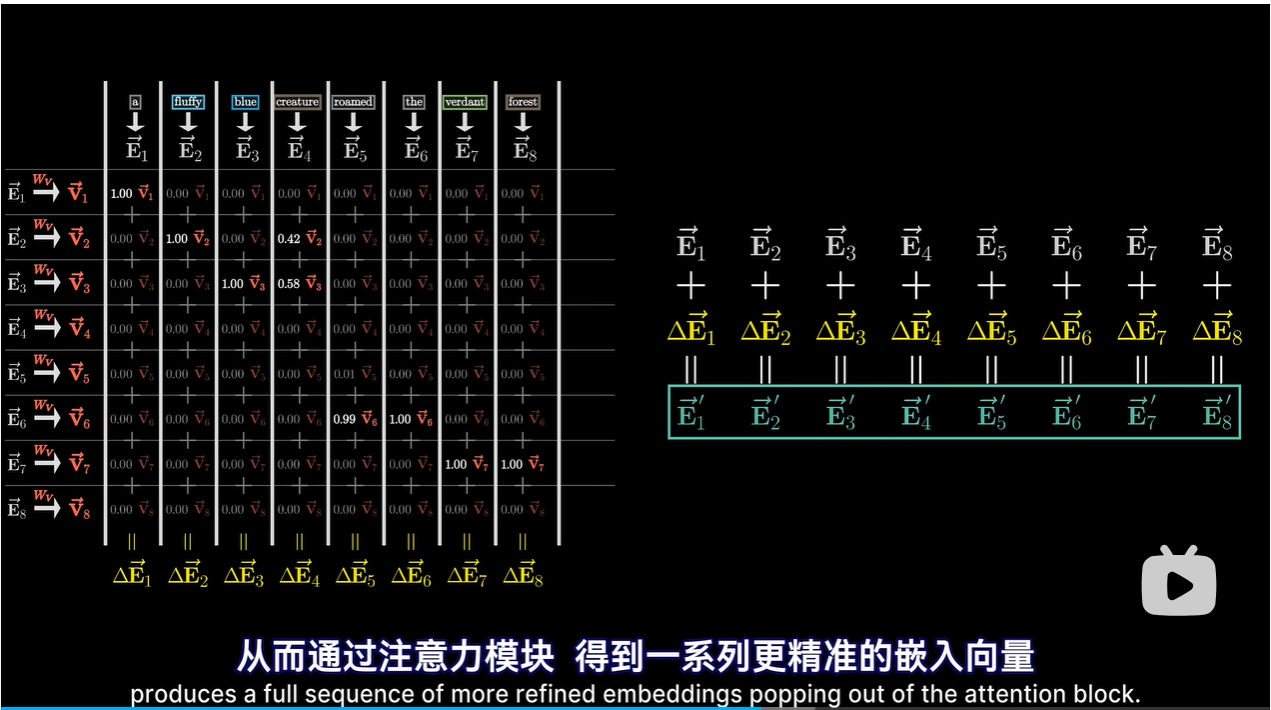
-

-

-
key query value矩阵:三种填满了可调参数的矩阵
-

-
V矩阵:输入与输出都存在于高维的嵌入空间中
-
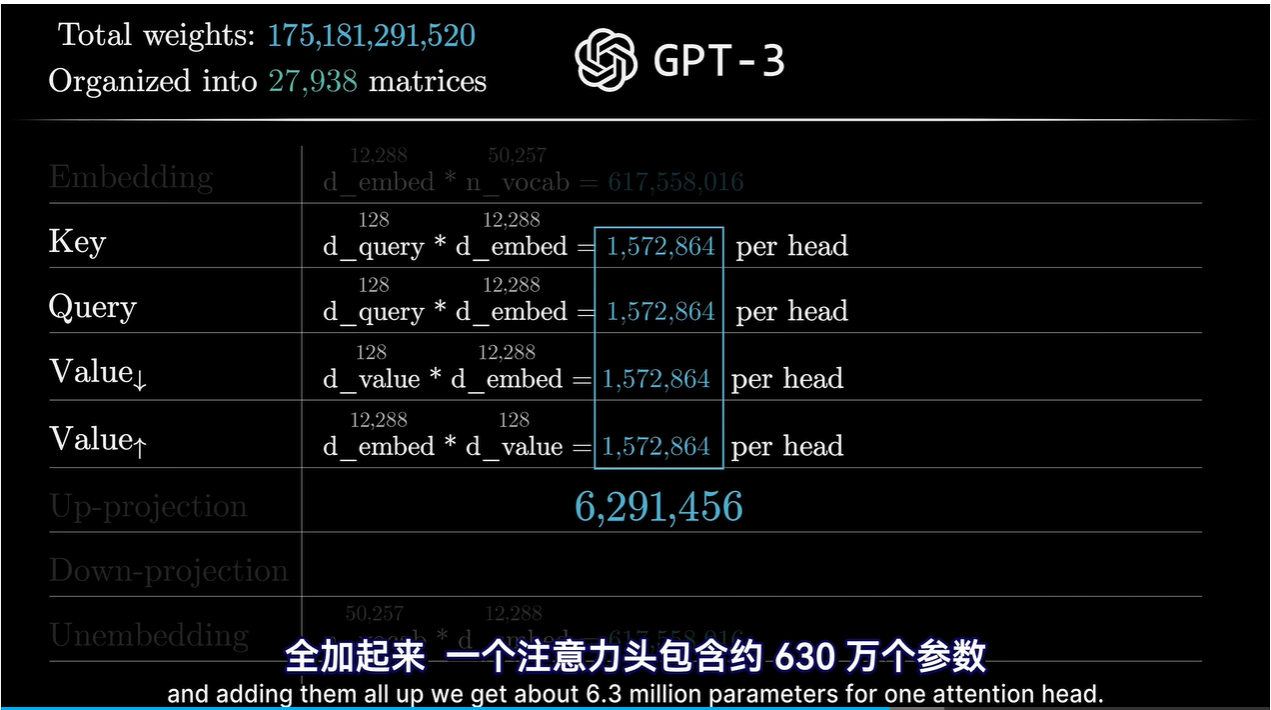
如果按照下图的方式,参数太多了 1.5亿个参数
-
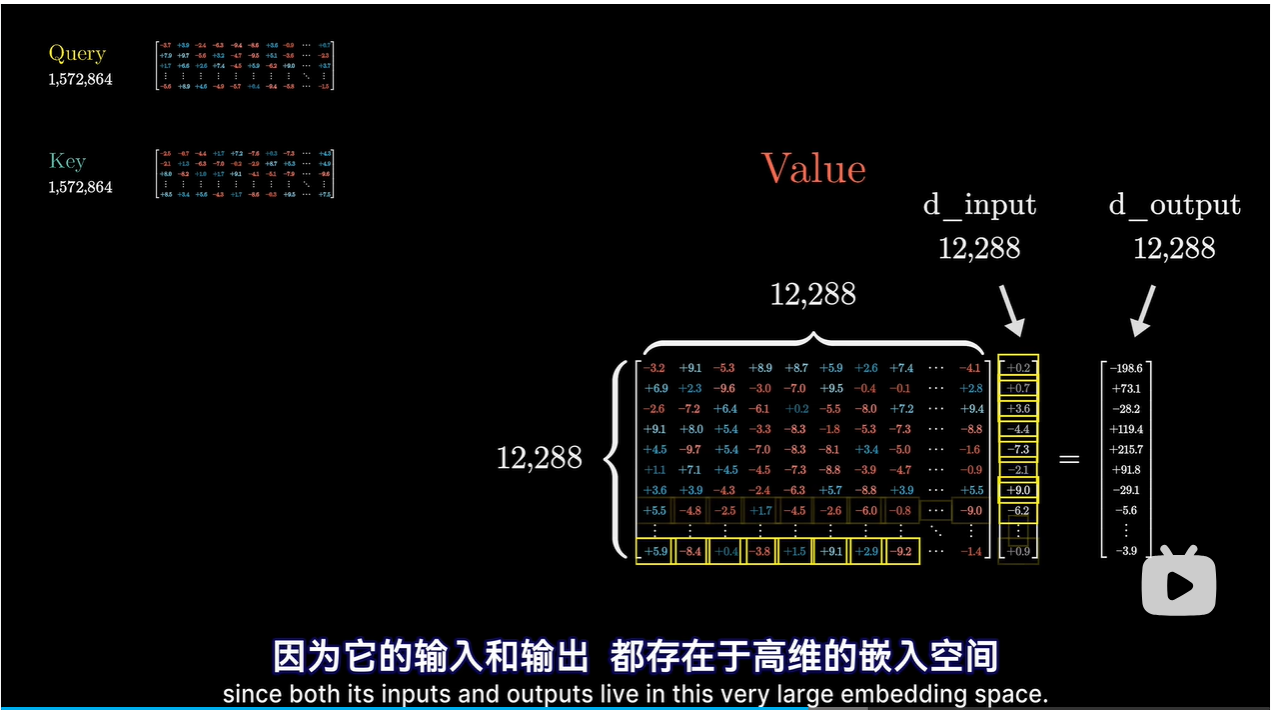
-
更有效的方式是值矩阵需要的参数量等于键矩阵和查询矩阵的参数量之和
-

-
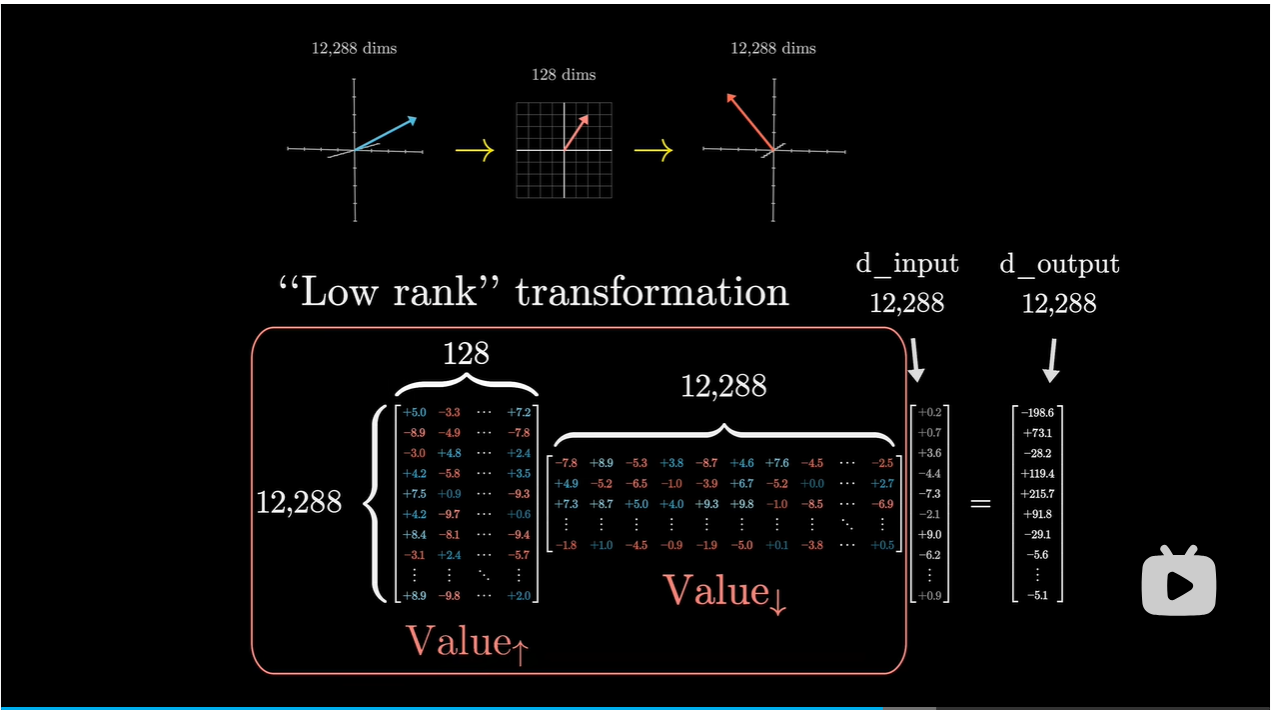
将值矩阵分解为两个小矩阵相乘,整体视为线性映射
-

-
右边:将较大的嵌入向量降维到较小的空间中
-
左边:将较小的向量映射到较大的嵌入空间中
-
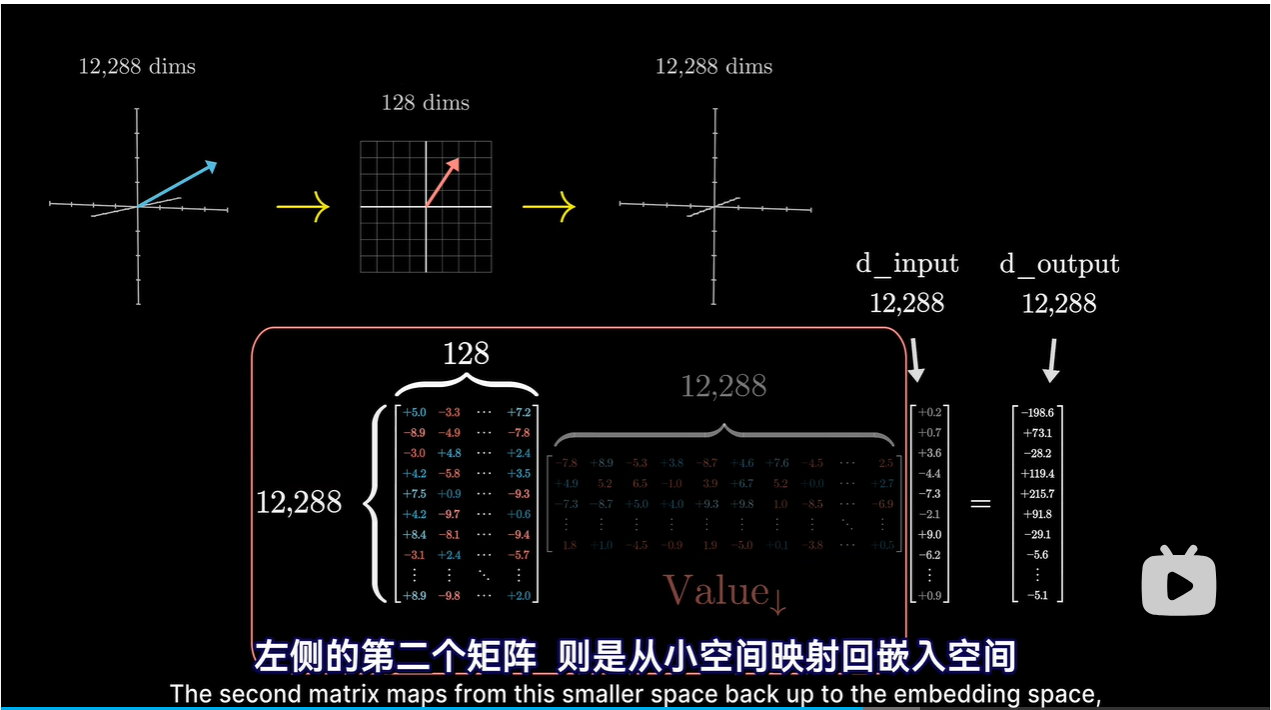
-
-
小节
4 多头注意力机制

- 96个不同的键和查询矩阵,会产生96种不同的注意力模式,每个注意力头有独特的值矩阵
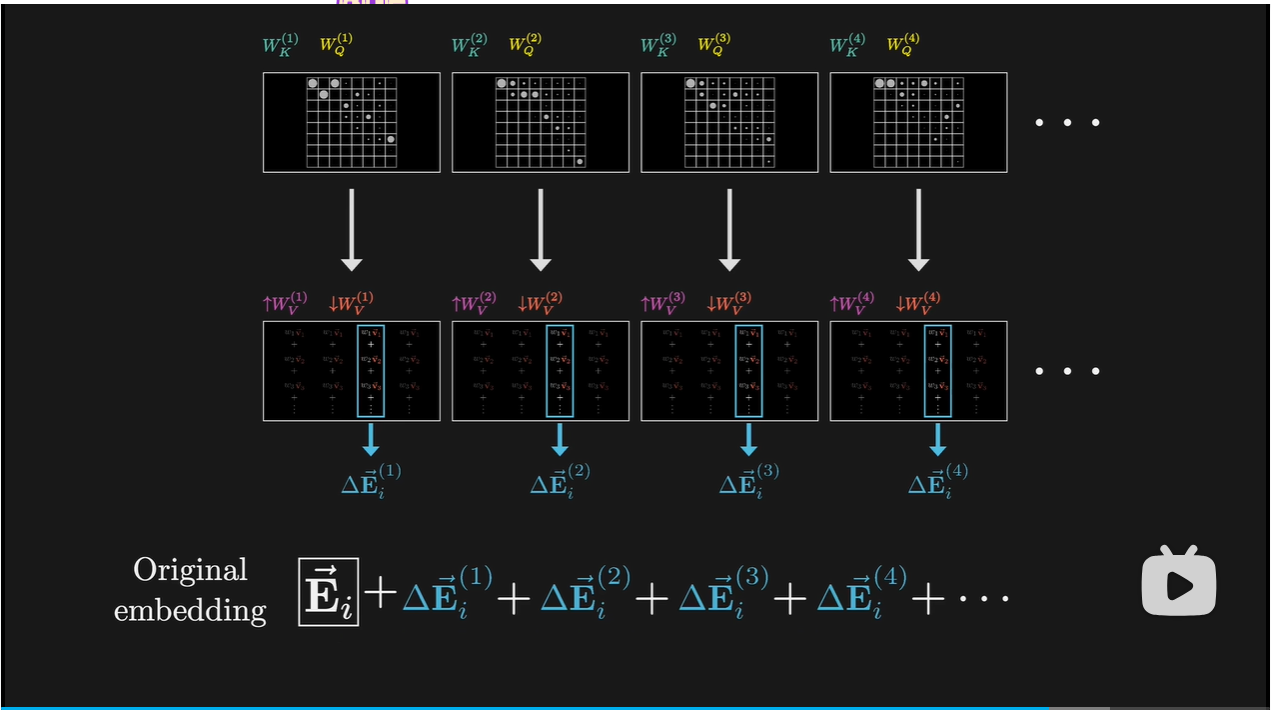
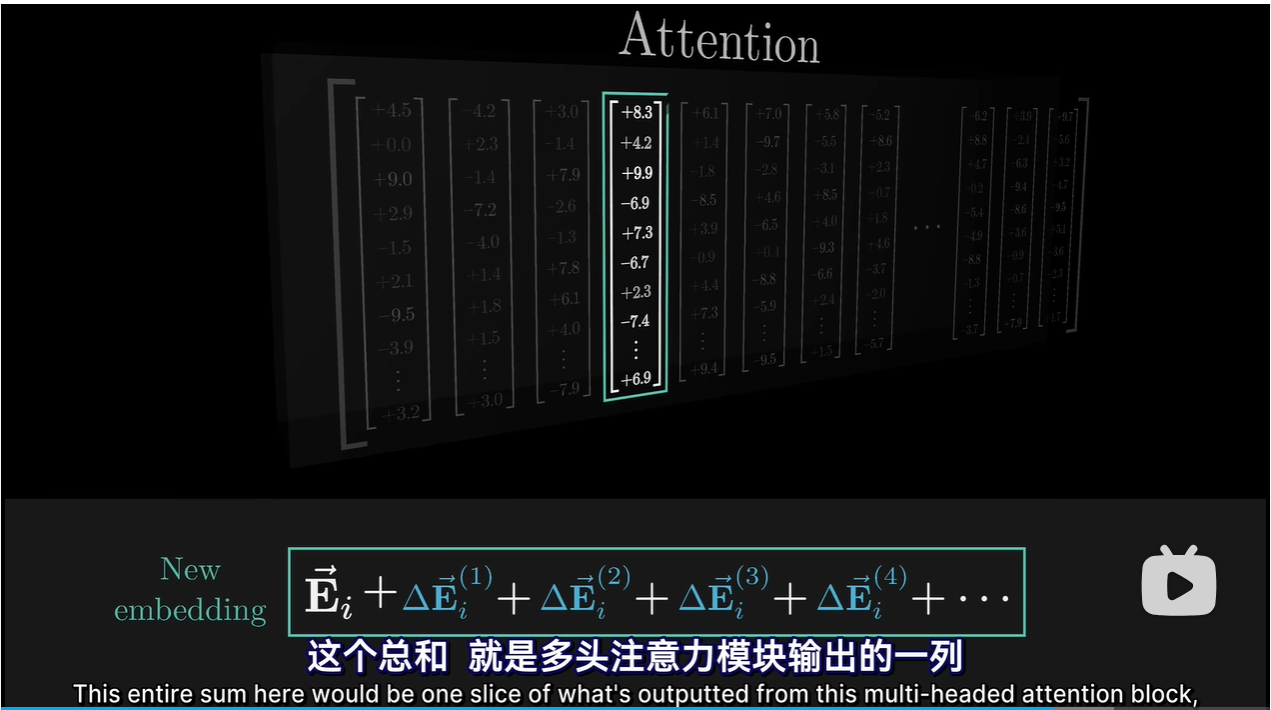
- 通过并行多头运算,模型能学到根据上下文改变语义的多种方式

- 多个结构不断迭代;某个词吸收上下文信息后,还有更多机会被周围含义细致的词语影响
- 修饰,语法结构,情感、语气、诗意、科学原理

三 架构静态分析
词嵌入层可以看做是查找表,用于获得每个单词的向量表示
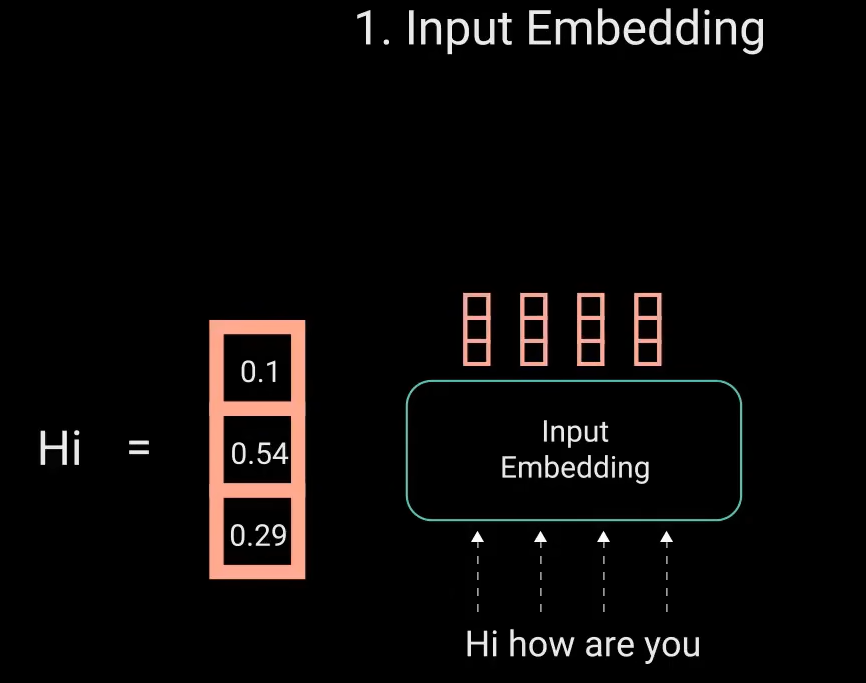
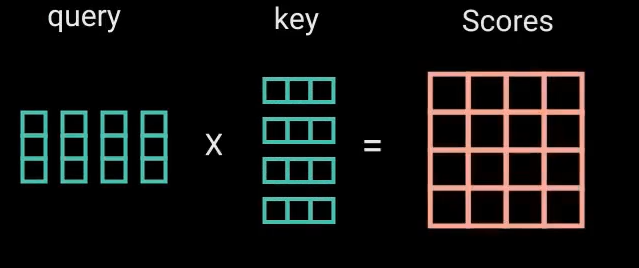
乘法可能产生爆炸效果,通过开平方让得分缩放
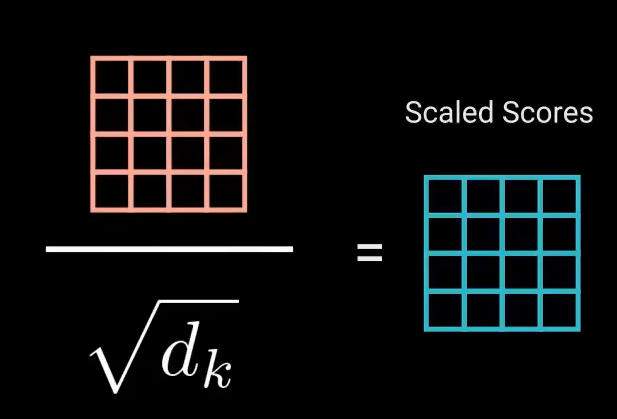

Softmax–较低的得分收到抑制,较高的得分得到增强。模型对于关注的词更有信息