问题现象

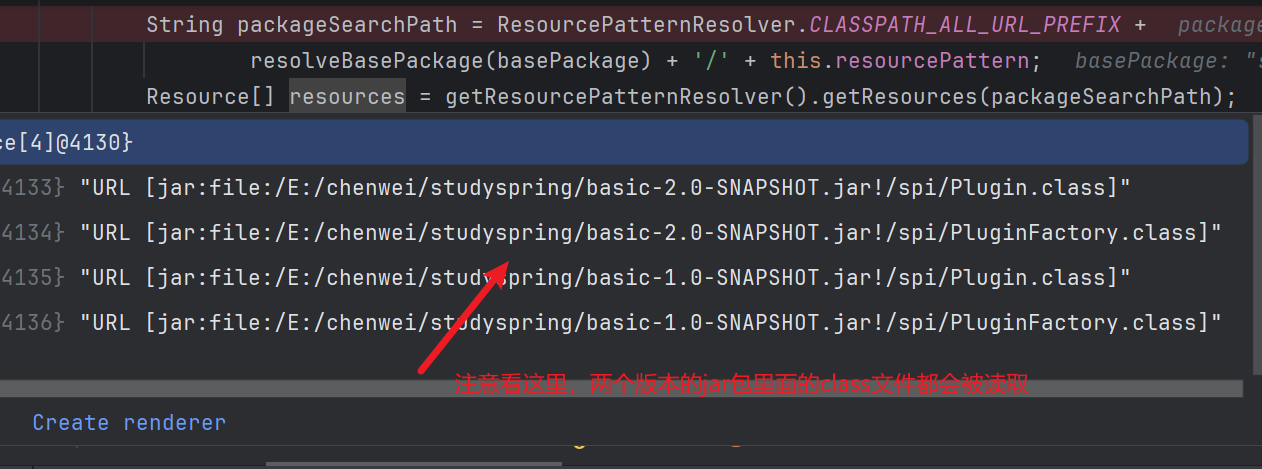
之前遇到过一个问题，在一个微服务的目录下有相同功能 jar 包的两个不同的版本，其中一个版本里面的类有 @Component 注解，另外一个版本的类里面没有 @Component 注解，且按照加载的顺序，没有 @Component 注解的 jar 包顺序还在前面，如下图所示：

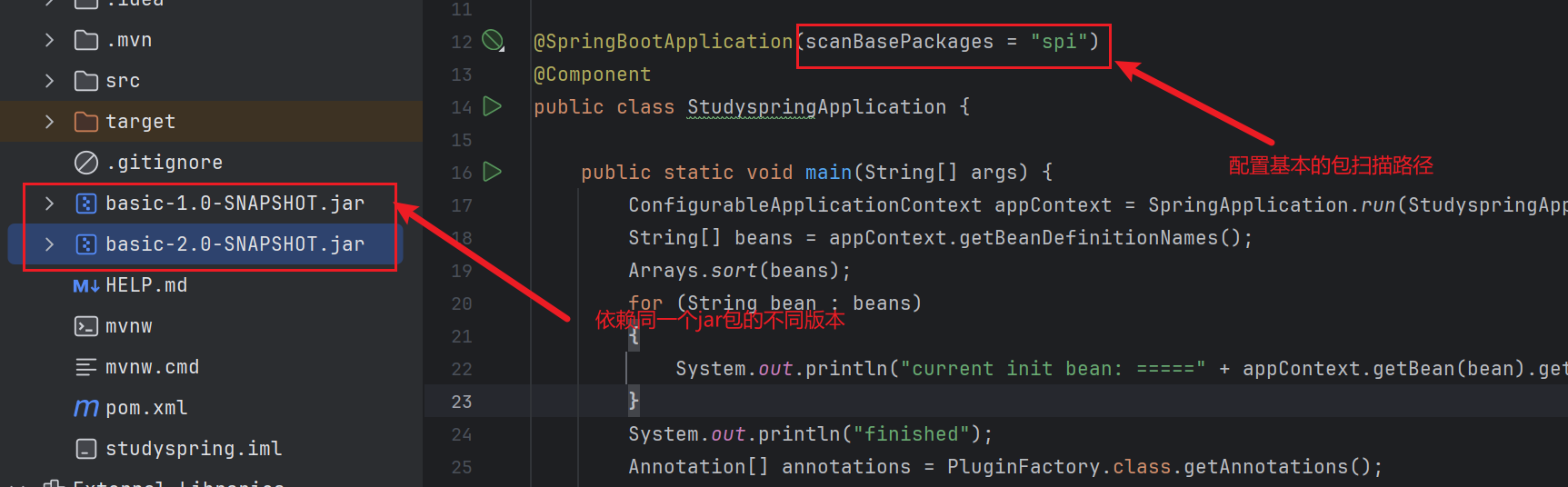
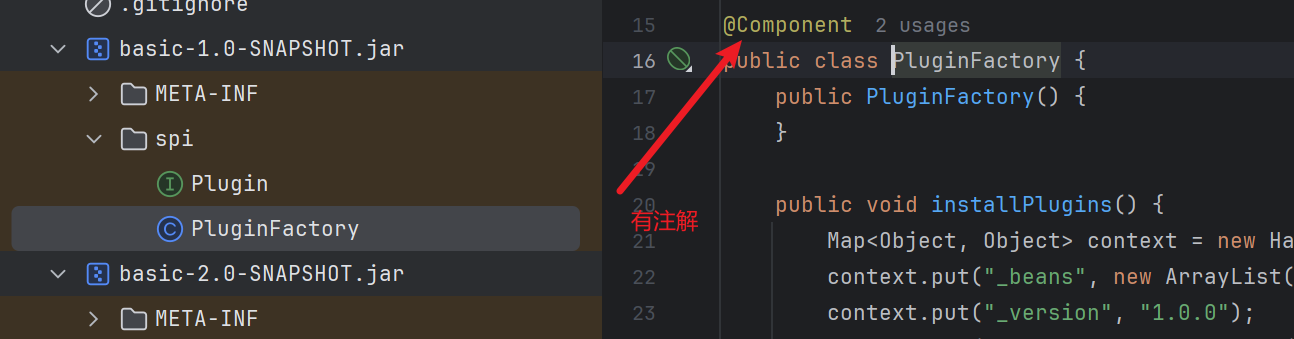
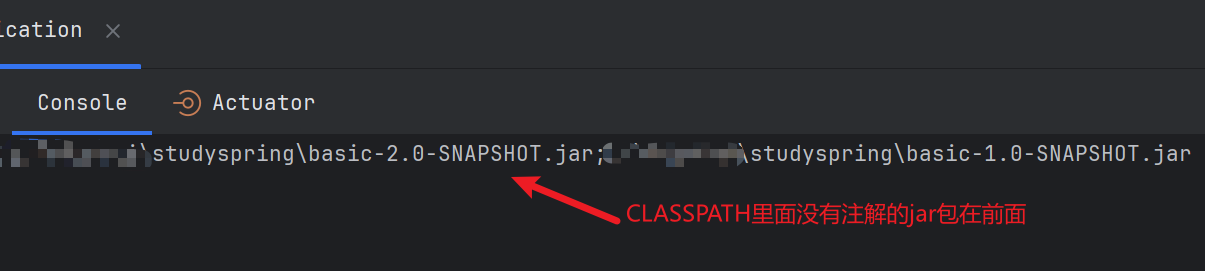
按照类加载的顺序来说，只会加载没有 @Component 注解的类，如下图所示：

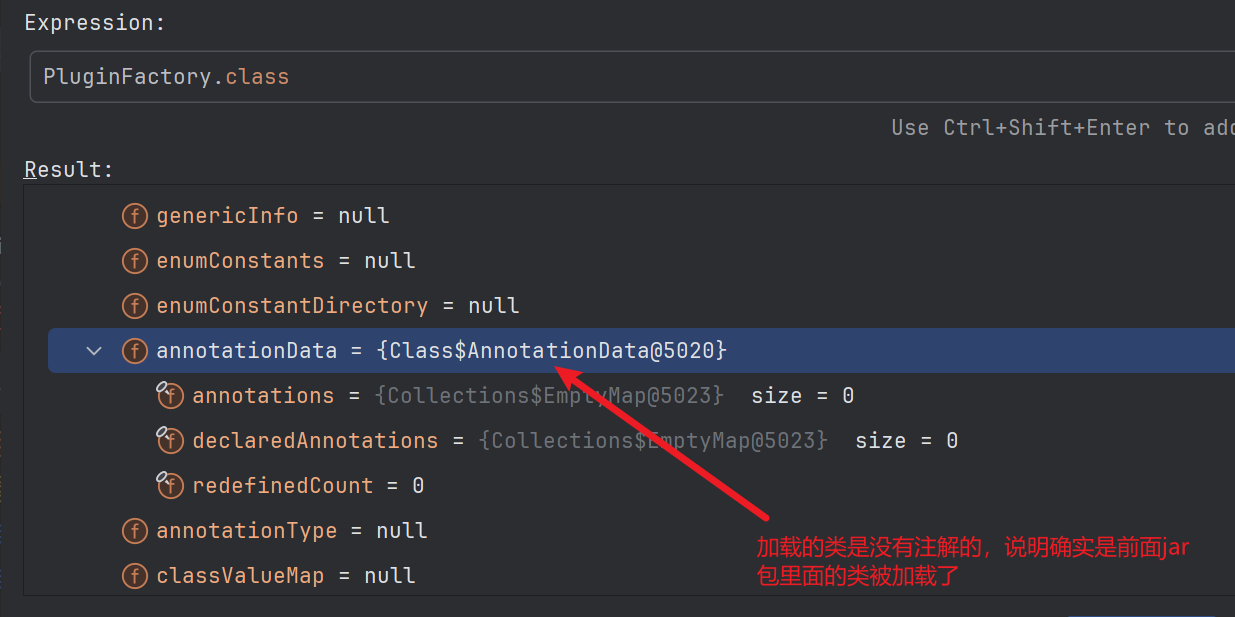
但是实际上发现 Spring 还是基于这个类创建了 Bean如下图所示：

为啥加载的类明明没有注解，但是 Spring 为什么还是创建了这个类的 Bean？初步猜测 Spring 不是通过读取已加载的类是否有 @Component 注解来判断是否要创建 Bean的。

源码剖析

Spring 中扫描注解修饰的 Bean 是在 ClassPathBeanDefinitionScanner#scanCandidateComponents() 方法里面实现的，这个方法里面会根据配置的 scanBasePackages 从 CLASSPATH 下所有的 jar 包里面去找符合这个包路径的类，如下图所示：



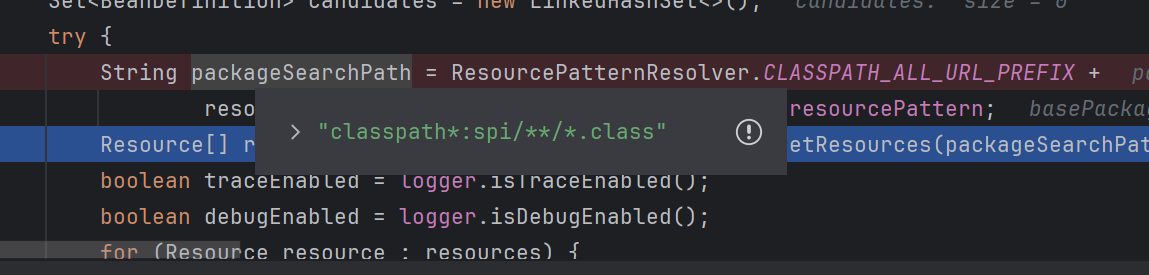
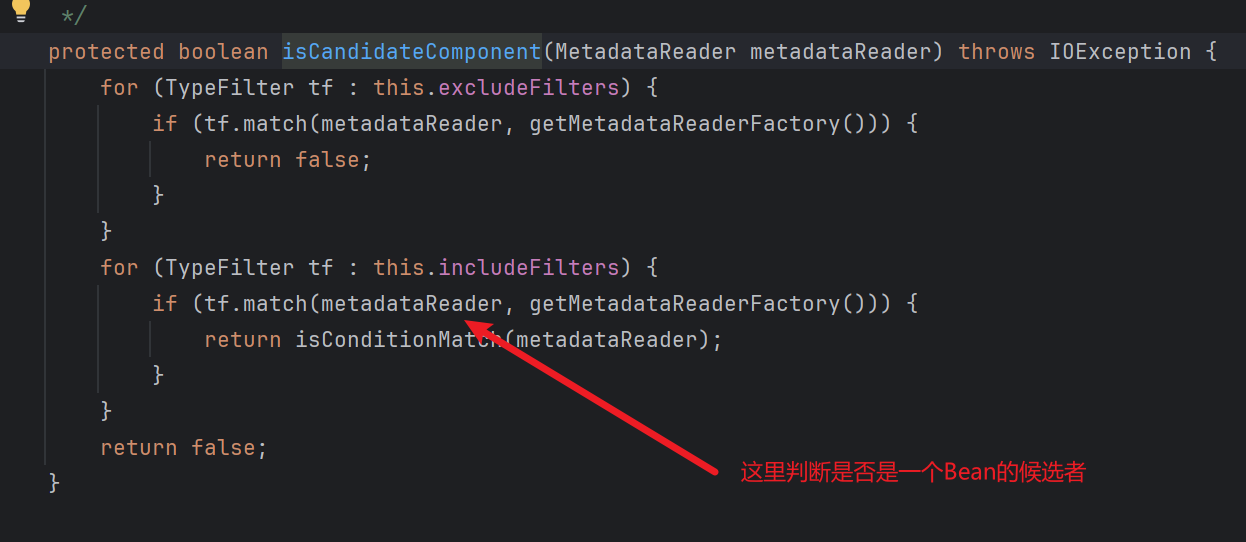
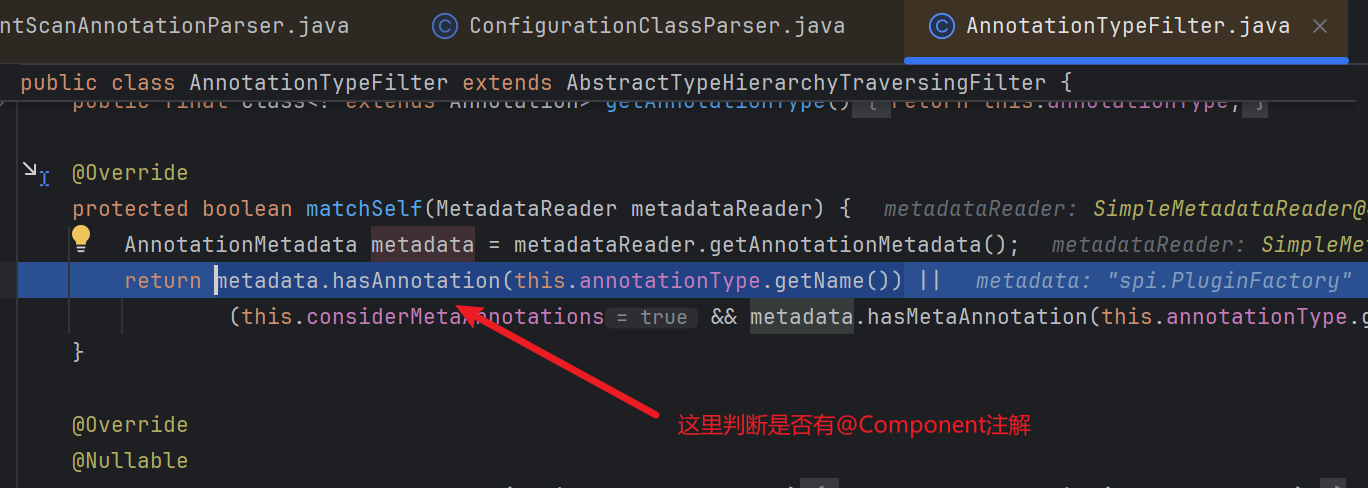
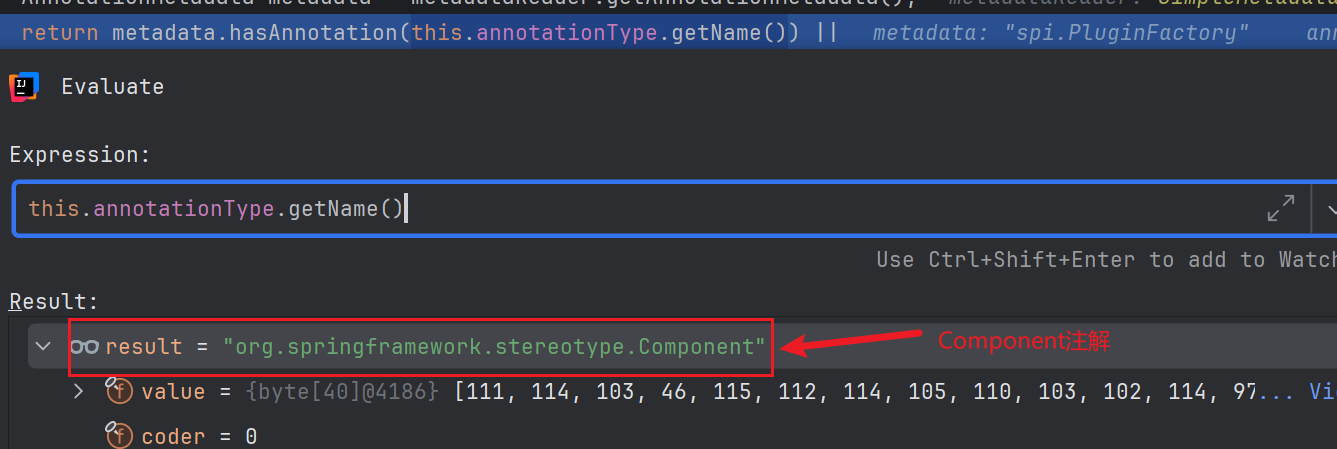
然后读取这些 Class 文件的内容，判断它们是否有 @Component 注解，如果有后续就会创建一个对应的 Bean。