代码随想录_刷题记录_第四次

news2024/9/29 6:02:56

二叉树 — 理论基础

种类：

  • 满二叉树（所有层的节点都是满的，k：深度 节点数量：2^k - 1）
  • 完全二叉树（除了最后一层，其余层全满，并且最后一层从左到右连续）
  • 二叉搜索树（对于每一个父节点来说，左子树的所有节点都小于父节点，右子树的所有节点都大于父节点 时间复杂度 ： log(n) ）
  • 平衡二叉搜索树（左子树和右子树的高度差不能大于1 时间复杂度：log(n)

存储方式：

  • 链式存储（左指针、右指针）
  • 线式存储（数组 父节点 i，左子节点 2i + 1，右子节点 2i + 2）

遍历方式：

  • 深度优先搜索：递归方式实现（前序、中序、后序）、迭代法（使用栈）
  • 广度优先搜索：一层一层的去遍历（迭代法，使用队列）（层序遍历）

前序：中左右 中序：左中右 后序：左右中

定义方法：

struct TreeNode{
	int value;
	TreeNode* left;
	TreeNode* right;
	TreeNode(int val) : value(val) left(NULL) right(NULL) {}
}

**二叉树节点的深度：**从根节点到该节点的最长简单路径边的条数（前序递归求深度）

**二叉树节点的高度：**从该节点到叶子节点（左右子节点都为空）的最长简单路径边的条数（后序递归求高度）

前序遍历求深度，后序遍历求高度

二叉树 — 递归遍历

递归遍历的三步骤：

  1. 确定递归函数的参数和返回值
  2. 确定终止条件
  3. 确定单层递归的逻辑

前序遍历

题目链接：144. 二叉树的前序遍历 - 力扣（LeetCode）

**题目要求：**给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

示例 ：

**输入：**root = [1,2,3,4,5,null,8,null,null,6,7,9]

输出：[1,2,4,5,6,7,3,8,9]

解释：

img

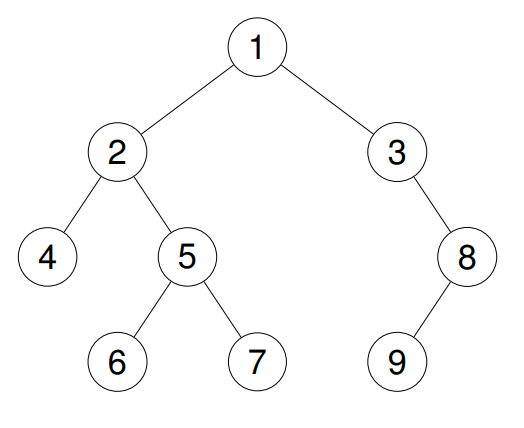
思路：

  1. 确定参数（根节点、vec数组）和返回值（void）

    void traversal(TreeNode* cur, vector<int>& vec)

  2. 确定终止条件（深度优先搜索，cur == NULL return）

    if (cur == NULL) return;

  3. 确定单层递归的逻辑

    vec.push_back(cur->val);    // 中
traversal(cur->left, vec);  // 左
traversal(cur->right, vec); // 右

解法：

  • C++
class Solution {
public:
    void traversal(TreeNode* cur, vector<int>& vec){
        if(cur == NULL) return;
        vec.push_back(cur->val);      // 中
        traversal(cur->left, vec);    // 左
        traversal(cur->right, vec);   // 右
    }

    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        traversal(root, result);   // 传入根节点和存放结果的数组
        return result;
    }
};

中序遍历

题目链接：94. 二叉树的中序遍历 - 力扣（LeetCode）

  • C++
class Solution {
public:
    void traversal(TreeNode* cur, vector<int>& vec){
        if(cur == NULL) return;
        traversal(cur->left, vec);    // 左
        vec.push_back(cur->val);      // 中
        traversal(cur->right, vec);   // 右
    }


    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        traversal(root, result);   // 传入根节点和存放结果的数组
        return result;
    }
};

后序遍历

题目链接：145. 二叉树的后序遍历 - 力扣（LeetCode）

  • C++
class Solution {
public:
    void traversal(TreeNode* cur, vector<int>& vec){
        if(cur == NULL) return;
        traversal(cur->left, vec);    // 左
        traversal(cur->right, vec);   // 右
        vec.push_back(cur->val);      // 中
    }

    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> result;
        traversal(root, result);   // 传入根节点和存放结果的数组
        return result;
    }
};

二叉树 — 迭代遍历

**递归的实现：**每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中，然后递归返回的时候，从栈顶弹出上一次递归的各项参数，所以这就是递归为什么可以返回上一层位置的原因

所以，我们使用栈也可以实现二叉树的前中后序遍历

前序遍历

**思路：**用栈存放节点，用数组存放结果

先将根节点放入栈中，进入循环直到栈为空，取出栈顶结点作为中间节点（中左右），放入这个节点的右子节点，再放入这个节点的左子节点（取出时是先取左子节点）（如果为空则不放入）

解法：

  • C++
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
    	vector<int> result;
        stack<TreeNode*> st;
        if(root == NULL) return result;
        st.push(root);   // 先将根节点放入栈中
        while(!st.empty()){
            TreeNode* cur = st.top();   // 取出栈顶结点作为这次的中间节点
            st.pop();           
            result.push_back(cur->val);
            if(cur->right) st.push(cur->right);   // 向栈中放入右子节点，如果为空则不放入
            if(cur->left)  st.push(cur->left);    // 向栈中放入左子节点
        } 
        return result;
    }
};

后序遍历

**思路：**跟前序遍历相同，只不过调转了左右子节点入栈的顺序，此时输出的结果为 中右左，所以需要调换顺序输出 左右中

解法：

  • C++
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
    	vector<int> result;
        stack<TreeNode*> st;
        if(root == NULL) return result;
        st.push(root);   // 先将根节点放入栈中
        while(!st.empty()){
            TreeNode* cur = st.top();   // 取出栈顶结点作为这次的中间节点
            st.pop();
            result.push_back(cur->val);
            if(cur->left)  st.push(cur->left);    // 向栈中放入左子节点
            if(cur->right) st.push(cur->right);   // 向栈中放入右子节点，如果为空则不放入
        }   
        reverse(result.begin(), result.end());    // 中右左 -> 左右中
        return result;
    }
};

中序遍历

思路：

写法与前序遍历、后序遍历不同，因为前序遍历和后序遍历的顺序是中左右、中右左（最后反转），要访问的元素和要处理的元素顺序是一致的，但是中序遍历 左中右 处理顺序和访问顺序是不一致的

所以，在使用迭代法写中序遍历的时候，就需要借用指针的遍历来帮助访问节点，栈则用来处理节点上的元素

解法：

  • C++
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        TreeNode* cur = root;
        while(cur || !st.empty()){
            if(cur){   // 向该子节点的左子节点一直遍历，直到为空
                st.push(cur);   // 将所有节点放入栈中
                cur = cur->left;
            }else{   // 若已经遍历到底
                cur = st.top();   // 取出栈顶元素（最左子节点）
                st.pop();
                result.push_back(cur->val);   // 放入左子节点
                cur = cur->right;   // 取出右子节点重复操作
            }
        }
        return result;
    }
};

二叉树 — 层序遍历

层序遍历 I

题目链接：102. 二叉树的层序遍历 - 力扣（LeetCode）

**题目要求：**给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

示例1：

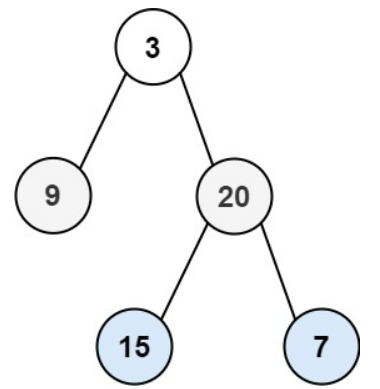
image-20240924171110192

输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

**思路：**借助队列保存每一层中遍历的元素

解法：

  • C++
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> que;
        vector<vector<int>> result;
        if(root == NULL) return result;
        que.push(root);
        while(!que.empty()){
            vector<int> vec;   // 保存每一层的节点数据
            int size = que.size();   // 记录每一层节点的数量
            for(int i = 0; i < size; i++){
                TreeNode* cur = que.front();   // 访问队列的头部元素
                que.pop();
                vec.push_back(cur->val);
                if(cur->left)  que.push(cur->left);
                if(cur->right) que.push(cur->right);
            }
            result.push_back(vec);
        }
        return result;
    }
};

二叉树的最大深度

题目链接：104. 二叉树的最大深度 - 力扣（LeetCode）

题目要求：

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

**思路：**仍然是使用队列保存每一层的数据，不过在进行层切换时要计数

解法：

  • C++
class Solution {
public:
    int maxDepth(TreeNode* root) {
        queue<TreeNode*> que;
        int result = 0;
        if(!root) return result;
        que.push(root);
        while(!que.empty()){
            result++;
            int size = que.size();
            while(size--){
                TreeNode* cur = que.front();
                que.pop();
                if(cur->left)  que.push(cur->left);
                if(cur->right) que.push(cur->right);
            }
        }
        return result;
    }
};

二叉树的最小深度

题目链接：111. 二叉树的最小深度 - 力扣（LeetCode）

题目要求：

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点（左右子节点都为 NULL 的节点）的最短路径上的节点数量。

**说明：**叶子节点是指没有子节点的节点。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：

输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

解法：

  • C++
class Solution {
public:
    int minDepth(TreeNode* root) {
        queue<TreeNode*> que;
        int result = 0;
        if(!root) return result;
        que.push(root);
        while(!que.empty()){
            result++;
            int size = que.size();
            while(size--){
                TreeNode* cur = que.front();
                que.pop();
                if(cur->left)  que.push(cur->left);
                if(cur->right) que.push(cur->right);
                if(!cur->left && !cur->right) // 当左子节点与右子节点都为空时就代表最小深度
                    return result;
            }
        }
        return result;
    }
};

二叉树 — 翻转二叉树

题目链接：226. 翻转二叉树 - 力扣（LeetCode）

**题目要求：**给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

img

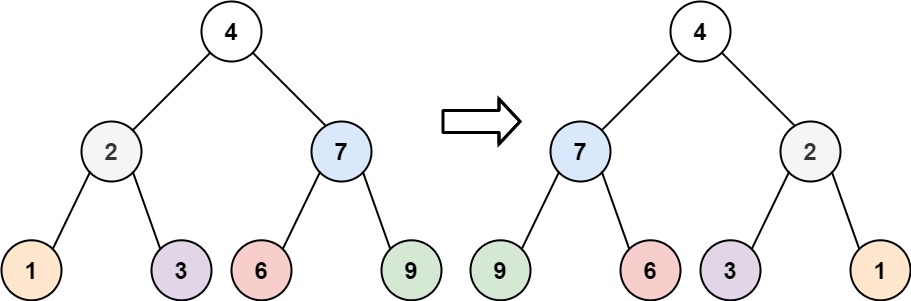
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

img

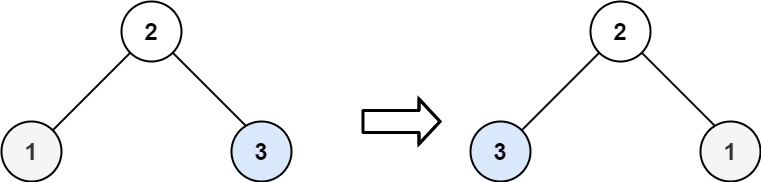
输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

输入：root = []
输出：[]

思路：

只要将每一个节点的左右子节点翻转一下，就可以达到整体翻转的效果

使用 前序/后续 对二叉树进行递归遍历，中序（会将某些节点的左右子节点翻转两次）

1、递归函数的参数（TreeNode *），返回值（TreeNode *）

TreeNode* invertTree(TreeNode* cur)

2、终止条件（root == NULL）

if (root == NULL) return NULL;

3、单层递归逻辑（交换传入节点的左右子节点）

swap(root->left, root->right);   // 交换两个变量的值
invertTree(root->left);
invertTree(root->right);

解法：

  • C++（前序遍历 递归）
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(!root) return NULL;
        swap(root->left,root->right); // 中
        invertTree(root->left);       // 左
        invertTree(root->right);      // 右
        return root;
    }
};
  • C++（后序遍历 递归）
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(!root) return NULL;
        invertTree(root->left);       // 左
        invertTree(root->right);      // 右
        swap(root->left,root->right); // 中
        return root;
    }
};

二叉树 — 对称二叉树

题目链接：101. 对称二叉树 - 力扣（LeetCode）

**题目要求：**给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

img

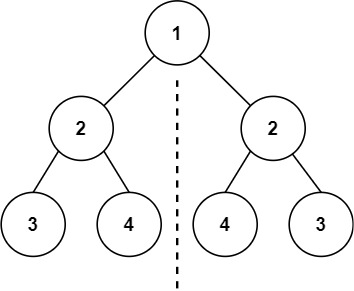
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

img

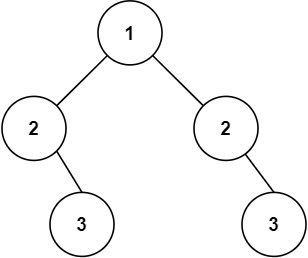
输入：root = [1,2,2,null,3,null,3]
输出：false

思路：

判断是否为对称二叉树，其实就是判断左子树和右子树是否可以相互翻转，真正要比较的是两个树（根节点的左右子树）（比较两个子树的里侧和外侧元素是否相等），所以在递归遍历的过程中，也是要同时遍历两棵树

只能使用后续遍历（左右中）

正因为要遍历两棵树而且要比较内测和外侧节点，所以准确来说是一个树的遍历顺序是左右中，一个树的遍历顺序是右左中

1、递归函数的参数（TreeNode* left TreeNode* right），返回值（bool）

bool compare(TreeNode* left, TreeNode* right)

2、确定终止条件

if (left == NULL && right != NULL) return false;
else if (left != NULL && right == NULL) return false;
else if (left == NULL && right == NULL) return true;
else if (left->val != right->val) return false;

3、确定单层递归的逻辑

bool outside = compare(left->left, right->right);   // 左子树：左、 右子树：右
bool inside = compare(left->right, right->left);    // 左子树：右、 右子树：左
bool isSame = outside && inside;                    // 左子树：中、 右子树：中（逻辑处理）
return isSame;

解法：

  • C++
class Solution {
public:
    bool compare(TreeNode* left, TreeNode* right){
        if(left == NULL && right == NULL) return true;
        else if(left != NULL && right == NULL) return false;
        else if(left == NULL && right != NULL) return false;
        else if(left->val != right->val) return false; // 这个条件已经比较了每一个节点的值

        bool cmp_left  = compare(left->left, right->right);
        bool cmp_right = compare(left->right, right->left);
        return cmp_left && cmp_right;
    }

    bool isSymmetric(TreeNode* root) {
        if(root == NULL) return true;
        return compare(root->left, root->right);
    }
};

二叉树 — 二叉树的最大深度

题目链接：104. 二叉树的最大深度 - 力扣（LeetCode）

**思路：**这里使用递归法，也可以使用层序遍历

使用前序递归求深度，使用后序递归求高度，而根节点的高度就是整个二叉树的深度，所以这道题实际上是使用后续递归求根节点的高度

1、确定递归的参数和返回值

int maxDepth(TreeNode* node)

2、确定终止条件（如果为空节点，就返回0，表示高度为0）

if (node == NULL) return 0;

3、单层递归的逻辑：先求它的左子树的深度，再求右子树的深度，最后取左右深度最大的数值 再+1 （加1是因为算上当前中间节点）就是目前节点为根节点的树的深度

int leftdepth = getdepth(node->left);       // 左
int rightdepth = getdepth(node->right);     // 右
int depth = 1 + max(leftdepth, rightdepth); // 中
return depth;

解法：

  • C++
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == NULL) return 0;
        int leftdepth  = maxDepth(root->left);       // 左
        int rightdepth = maxDepth(root->right);      // 右
        int depth = 1 + max(leftdepth, rightdepth);  // 中
        return depth;
    }
};

二叉树 — 二叉树的最小深度

题目链接：111. 二叉树的最小深度 - 力扣（LeetCode）

**思路：**依旧是前序递归遍历求深度，后序递归遍历求高度

这里使用后序遍历求最小深度

最小深度是从根节点到最近叶子节点（左右子节点都为空）的最短路径上的节点数量。

1、确定递归函数的参数和返回值

int minDepth(TreeNode* node)

2、确定终止条件（遇到空节点，返回 0）

if(node == NULL) return 0;

3、确定单层递归的逻辑

int leftDepth = getDepth(node->left);
int rightDepth = getDepth(node->right);
// 当只有一个子节点时，就顺着这个子节点继续往下查
if(node->left == NULL && node->right != NULL){
	return 1 + rightDepth;
}
if(node->left != NULL && node->right == NULL){
	return 1 + leftDepth;
}
int result = 1 + min(leftDepth, rightDepth);
return result;

解法：

  • C++
class Solution {
public:
    int minDepth(TreeNode* root) {
        int result = 0;
        if(root == NULL) return 0;
        int leftDepth  = minDepth(root->left);   // 左
        int rightDepth = minDepth(root->right);  // 右
        if(root->left == NULL && root->right != NULL){
            return rightDepth + 1;
        }
        if(root->left != NULL && root->right == NULL){
            return leftDepth + 1;
        }
        result = 1 + min(leftDepth, rightDepth);
        return result;
    }
};

二叉树 — 完全二叉树的节点数量

题目链接：222. 完全二叉树的节点个数 - 力扣（LeetCode）

题目要求：

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例 1：

img

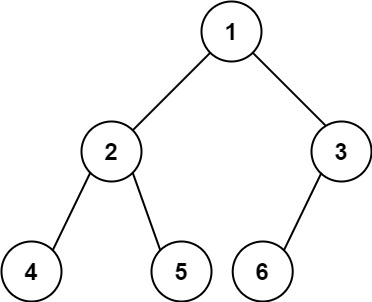
输入：root = [1,2,3,4,5,6]
输出：6

示例 2：

输入：root = []
输出：0

示例 3：

输入：root = [1]
输出：1

**思路：**可以使用层序遍历（只需要在遍历每一层时，记录节点的个数就可以），

使用递归的写法和求二叉树的深度写法类似，顺序依旧是后序（左右中）

1、确定递归的参数和返回值

int getNodesNum(TreeNode* cur)

2、确定终止条件（如果为空姐点的话，就返回 0，表示节点数量为 0）

if(cur == NULL) return 0;

3、确定单层递归的逻辑

int leftNum  = getNodesNum(cur->left);  // 左
int rightNum = getNodesNum(cur->right); // 右
int treeNum  = leftNum + rightNum + 1;  // 中
return treeNum;

解法：

  • C++
class Solution {
public:
    int countNodes(TreeNode* root) {
        if(root == NULL) return 0;
        int leftNum  = countNodes(root->left);
        int rightNum = countNodes(root->right);
        int result = leftNum + rightNum + 1;
        return result;
    }
};

示例 3：*

输入：root = [1]
输出：1

**思路：**可以使用层序遍历（只需要在遍历每一层时，记录节点的个数就可以），

使用递归的写法和求二叉树的深度写法类似，顺序依旧是后序（左右中）

1、确定递归的参数和返回值

int getNodesNum(TreeNode* cur)

2、确定终止条件（如果为空姐点的话，就返回 0，表示节点数量为 0）

if(cur == NULL) return 0;

3、确定单层递归的逻辑

int leftNum  = getNodesNum(cur->left);  // 左
int rightNum = getNodesNum(cur->right); // 右
int treeNum  = leftNum + rightNum + 1;  // 中
return treeNum;

解法：

  • C++
class Solution {
public:
    int countNodes(TreeNode* root) {
        if(root == NULL) return 0;
        int leftNum  = countNodes(root->left);
        int rightNum = countNodes(root->right);
        int result = leftNum + rightNum + 1;
        return result;
    }
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2175995.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

LINUX--调度未来任务

LINUX--调度未来任务

crontab 文件中的用户作业时间格式怎么解释&#xff1f; * * * * * command 分 时 日 月 周 x-y表示范围&#xff0c;包括x,y的值 */x 表示x的间隔 x,y表示列表&am…
阅读更多...
内容付费平台开发中的数据安全与用户隐私保护

内容付费平台开发中的数据安全与用户隐私保护

在内容付费平台的开发过程中&#xff0c;数据安全与用户隐私保护至关重要。保护用户的信息不仅是法律要求&#xff0c;更是建立用户信任的基础。本文将探讨如何在内容付费平台中实现数据安全与隐私保护&#xff0c;并提供一些相关的技术代码示例。 1. 数据加密 数据加密是保…
阅读更多...
timedatectl命令：告别时间烦恼，一键同步系统时间

timedatectl命令：告别时间烦恼，一键同步系统时间

一、命令简介 ​timedatectl​ 命令用于查看和设置系统的时间和日期&#xff0c;以及配置时区和 NTP&#xff08;Network Time Protocol&#xff09;设置。 相关命令&#xff1a;cal ​显示日历、 date ​查看、设置日期 ‍ 二、命令参数 格式&#xff1a; timedatectl […
阅读更多...
InnoDB索引结构

InnoDB索引结构

文章目录 索引数据结构聚集索引非聚集索引 索引维护顺序插入和随机插入为什么预留空间 索引构建过程页的合并拆分 索引数据结构 https://dev.mysql.com/doc/refman/8.4/en/innodb-physical-structure.html 除了空间索引&#xff08;spatial index&#xff09;使用R-tree之外&a…
阅读更多...
RTMP、RTSP直播播放器的低延迟设计探讨

RTMP、RTSP直播播放器的低延迟设计探讨

技术背景 没有多少开发者会相信RTMP或RTSP播放器&#xff0c;延迟会做到150-300ms内&#xff0c;除非测试过大牛直播SDK的&#xff0c;以Android平台启动轻量级RTSP服务和推送RTMP&#xff0c;然后Windows分别播放RTSP和RTMP为例&#xff0c;整体延迟如下&#xff1a; 大牛直播…
阅读更多...
FastAPI 第六课 -- 请求和响应

FastAPI 第六课 -- 请求和响应

目录 一. 前言 二. 请求数据 2.1. 查询参数 2.2. 路径参数 2.3. 请求体 三. 响应数据 3.1. 返回 JSON 数据 3.2. 返回 Pydantic 模型 3.3. 请求头和 Cookie 四. 重定向和状态码 五. 自定义响应头 一. 前言 在 FastAPI 中&#xff0c;请求&#xff08;Request&#…
阅读更多...
【web安全】——信息收集

【web安全】——信息收集

一、收集域名信息 1.1域名注册信息 工具&#xff1a;站长之家 whois查询 SEO综合查询 1.2子域名收集 原理&#xff1a;字典爆破&#xff0c;通过字典中的各种字符串与主域名拼接&#xff0c;尝试访问。 站长之家 直接查询子域名 ip138.com https://phpinfo.me/domain/ …
阅读更多...
【源码+文档+调试讲解】美食推荐系统Python

【源码+文档+调试讲解】美食推荐系统Python

摘 要 随着我国经济的高速发展与人们生活水平的日益提高&#xff0c;人们对生活质量的追求也多种多样。尤其在人们生活节奏不断加快的当下&#xff0c;人们更趋向于足不出户解决生活上的问题&#xff0c;豆果美食推荐系统展现了其蓬勃生命力和广阔的前景。与此同时&#xff0c…
阅读更多...
第十四届蓝桥杯真题Python c组F.棋盘(持续更新)

第十四届蓝桥杯真题Python c组F.棋盘(持续更新)

博客主页&#xff1a;音符犹如代码系列专栏&#xff1a;蓝桥杯关注博主&#xff0c;后期持续更新系列文章如果有错误感谢请大家批评指出&#xff0c;及时修改感谢大家点赞&#x1f44d;收藏⭐评论✍ 【问题描述】 小蓝拥有 n n 大小的棋盘&#xff0c;一开始棋盘上全都…
阅读更多...
【韩顺平Java笔记】第2章：Java概述

【韩顺平Java笔记】第2章：Java概述

按视频的标号来对应小标题&#xff0c;自用学习笔记 文章目录 5. 内容梳理6. 程序举例6.1 什么是程序 7. Java故事7.1 Java诞生小故事7.2 Java技术体系平台 8. Java特性8.1 Java重要特点 9. sublime10. jdk介绍10.1 Java运行机制及运行过程10.1.1 Java虚拟机&#xff08;JVM&a…
阅读更多...
基于ASRPRO的语音应答

基于ASRPRO的语音应答

做这个的起因是为了送女朋友&#xff0c;而且这东西本身很简单&#xff0c;所以在闲暇之余尝试了一下。 这个工程很简单&#xff0c;只通过对ASRPRO进行编程即可。 先看效果。&#xff08;没有展示所有效果&#xff0c;后续会列出来所有对话触发&#xff09; 语音助手示例1 语音…
阅读更多...
AI驱动TDSQL-C Serverless 数据库技术实战营-与AI的碰撞

AI驱动TDSQL-C Serverless 数据库技术实战营-与AI的碰撞

目录 一、简介 二、实验介绍 三、结果展示 四、实操指导 4.1 系统设计 4.2 环境搭建&#xff08;手把手教程&#xff09; 4.3 应用构建 4.4 效果展示 4.5 踩坑避雷总结 五、清理资源 5.1 删除TDSQL-C Serverless 5.2 删除 HAI 算力 六、实验总结归纳 一、简介 本…
阅读更多...
Netty系列-5 Netty启动流程

Netty系列-5 Netty启动流程

背景 Netty程序有固定的模板格式&#xff0c;以ServerBootstrap为例: public class NettyServer {public void start(int port) {ServerBootstrap serverBootstrap new ServerBootstrap();EventLoopGroup boosGroup new NioEventLoopGroup(1);EventLoopGroup workGroup ne…
阅读更多...
番外篇 | 应对遮挡挑战，北航提出新型模型YOLOv5-FFM表现优异

番外篇 | 应对遮挡挑战，北航提出新型模型YOLOv5-FFM表现优异

前言：Hello大家好，我是小哥谈。在本文中，作者提出了一种改进的轻量级YOLOv5-FFM模型来解决行人检测遮挡问题。为了实现目标，作者在YOLOv5模型框架基础上进行了改进，并引入了Ghost模块和SE模块。此外，作者还设计了一个局部特征融合模块（FFM）来处理行人检测中的遮挡问题。…
阅读更多...
【题解】2022ICPC杭州-K

【题解】2022ICPC杭州-K

翻译 原题链接   简述一下就是每次询问重新定义一个字母排序表&#xff0c;问在这个顺序下n个字符串的序列的逆序数是多少。 字典树计算逆序数 先考虑初始状况下&#xff0c;即 a < b < . . . < z a<b<...<z a<b<...<z的情况下&#xff0c;逆序…
阅读更多...
基于PI控制器的车辆行驶控制系统simulink建模与仿真

基于PI控制器的车辆行驶控制系统simulink建模与仿真

目录 1.课题概述 2.系统仿真结果 3.核心程序与模型 4.系统原理简介 4.1 步骤一: 确定目标与测量 4.2 步骤二: 计算误差 4.3 步骤三: 设计PI控制器 4.4 步骤四: 应用控制信号 4.5 步骤五: 反馈循环 5.完整工程文件 1.课题概述 基于PI控制器的车辆行驶控制系统是一种常…
阅读更多...
Hive数仓操作（一）

Hive数仓操作（一）

Hive 介绍 Hive 是一个基于 Hadoop 的数据仓库工具&#xff0c;旨在简化大规模数据集的管理和分析。它将结构化数据文件映射为表&#xff0c;并提供类似 SQL 的查询功能。Hive 的数据存储在 Hadoop 分布式文件系统&#xff08;HDFS&#xff09;中&#xff0c;使用 Hive 查询语…
阅读更多...
使用MessagePipe实现进程间通信

使用MessagePipe实现进程间通信

1、MessagePipe介绍 可以用于.NET和Unity上面的高性能的内存/分布式消息传递管道。适用于发布/订阅模式、CQRS的中介模式、Prism中的EventAggregator、IPC&#xff08;进程间通信&#xff09;-RPC等。 支持&#xff1a; 依赖注入过滤器管道更好的事件同步/异步带键值的/无键…
阅读更多...
信息安全工程师（26）物理安全概念与要求

信息安全工程师（26）物理安全概念与要求

前言 物理安全是网络安全体系中的重要组成部分&#xff0c;它关注于保护物理环境、设备和资源免受未经授权的访问、破坏、损坏或盗窃。 一、物理安全概念 物理安全&#xff0c;也称为实体安全&#xff0c;是指通过采取各种物理措施来保护支持网络信息系统运行的硬件&#xff08…
阅读更多...
【Qt】Qt中的窗口坐标 信号与槽

【Qt】Qt中的窗口坐标 信号与槽

Qt中的窗口坐标 && 信号与槽 1. Qt中的窗口坐标2. 信号与槽的概述3. 信号和槽的使用3.1 connect函数的使用3.2 查看内置信号和槽3.2 connect的参数类型不匹配问题 4. 自定义信号 && 自定义槽4.1 自定义槽4.2 自定义信号 5. 带参数的信号和槽6. 信号与槽的关联方…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023