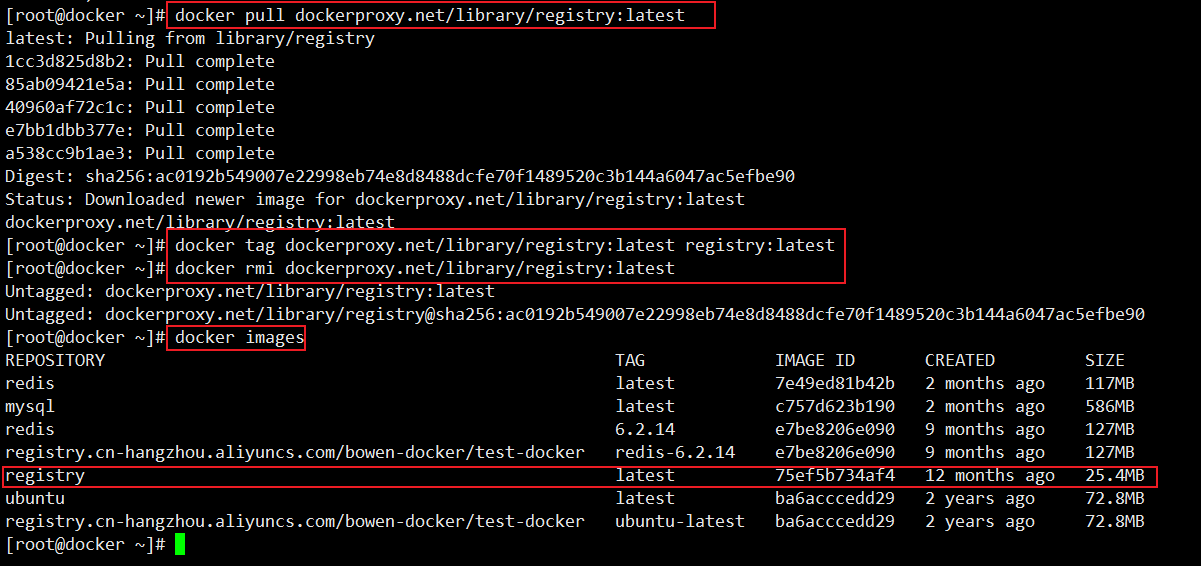
文章目录
- 数据集(Dataset)
- 特征(Feature)
- 标签(Label)
- 训练集(Training Set)
- 测试集(Test Set)
- 验证集(Validation Set)
- 模型(Model)
- 损失函数(Loss Function)
- 优化器(Optimizer)
- 超参数(Hyperparameter)
- 过拟合(Overfitting)
- 欠拟合(Underfitting)
- 交叉验证(Cross-Validation)
- 准确率(Accuracy)
- 精确率(Precision)
- 召回率(Recall)
- F1分数(F1 Score)
- ROC曲线(ROC Curve)
- AUC(Area Under Curve)
- Baseline(基线)
- Benchmark(基准)
- SOTA(State of the Art,最先进)
- 神经网络量化(Neural Network Quantization)
- 大模型量化(Large Model Quantization)
数据集(Dataset)
定义:用于训练和测试模型的数据集合。
示例:MNIST数据集包含手写数字的图像和标签。
特征(Feature)
定义:数据中的单个可测量属性或特性。
示例:在房价预测中,房屋面积、卧室数量等都是特征。
标签(Label)
定义:数据集中已知的输出值,通常用于监督学习任务。
示例:在图像分类中,标签可以是“猫”或“狗”。
训练集(Training Set)
定义:用于训练模型的数据子集。
示例:在训练分类器时,训练集包含输入数据和对应的标签。
测试集(Test Set)
定义:用于评估模型性能的数据子集,通常不用于训练。
示例:在模型训练完成后,使用测试集来评估模型的准确率。
验证集(Validation Set)
定义:用于调整模型超参数的数据子集,通常不用于训练。
示例:在交叉验证中,验证集用于选择最佳的超参数。
模型(Model)
定义:从输入数据中学习到的表示或函数,用于进行预测或决策。
示例:线性回归模型、决策树模型等。
损失函数(Loss Function)
定义:用于衡量模型预测值与真实值之间差异的函数。
示例:均方误差(MSE)、交叉熵损失等。
优化器(Optimizer)
定义:用于最小化损失函数的算法。
示例:随机梯度下降(SGD)、Adam优化器等。
超参数(Hyperparameter)
定义:在模型训练之前设置的参数,通常需要手动调整。
示例:学习率、正则化系数等。
过拟合(Overfitting)
定义:模型在训练数据上表现很好,但在测试数据上表现很差的现象。
示例:模型过于复杂,记住了训练数据的噪声。
欠拟合(Underfitting)
定义:模型在训练数据和测试数据上都表现不佳的现象。
示例:模型过于简单,无法捕捉数据的复杂模式。
交叉验证(Cross-Validation)
定义:一种评估模型性能的方法,通过将数据集分成多个子集进行训练和验证。
示例:K折交叉验证。
准确率(Accuracy)
定义:模型预测正确的比例。
示例:分类任务中,准确率是正确分类的样本数除以总样本数。
精确率(Precision)
定义:在所有预测为正类的样本中,实际为正类的比例。
示例:在垃圾邮件检测中,精确率是正确检测为垃圾邮件的比例。
召回率(Recall)
定义:在所有实际为正类的样本中,预测为正类的比例。
示例:在疾病检测中,召回率是正确检测出患病者的比例。
F1分数(F1 Score)
定义:精确率和召回率的调和平均值,用于综合评估模型的性能。
示例:在分类任务中,F1分数是精确率和召回率的平衡指标。
ROC曲线(ROC Curve)
定义:接收者操作特征曲线,用于评估二分类模型的性能。
示例:ROC曲线下的面积(AUC)用于衡量模型的分类能力。
understanding-auc-roc-curve
Receiver_operating_characteristic

AUC(Area Under Curve)
定义:ROC曲线下的面积,用于评估二分类模型的整体性能。
示例:AUC值越高,模型性能越好。
Baseline(基线)
定义:基线是指一套方法或模型,通常是简单或基本的,用于作为比较其他更复杂或更高级模型的起点。基线模型的目的是提供一个性能的基准,以便评估更复杂模型的改进是否显著。
作用:
性能参考:基线模型提供了一个性能的最低标准。如果一个复杂的模型不能显著优于基线模型,那么这个复杂模型可能不值得使用。
简化评估:通过比较复杂模型与基线模型的性能差异,可以更容易地评估复杂模型是否带来了实质性的改进。
研究透明度:在研究论文或报告中,通常会包含基线模型的结果,以增加研究的透明度和可重复性。
示例:在自然语言处理(NLP)任务中,BERT模型可以作为基线模型,用于比较新模型的性能。如果你的新模型能够超越BERT,那么你的研究就具有实际意义。
Benchmark(基准)
定义:基准是指一个目前最高的可量化指标,通常用于评估和比较不同算法或模型性能的标准测试集或任务。基准测试通常包括一个或多个标准化的数据集、特定的机器学习任务以及用于衡量模型性能的指标。
作用:
比较算法:通过在相同的基准上测试不同的算法,可以客观地比较它们的性能。
评估模型:帮助开发者了解模型的优缺点,以及在不同条件下的表现。
标准化:确保不同研究者和开发者使用相同的标准来评估他们的模型,从而促进研究的可重复性和透明度。
示例:在NLP任务中,BERT模型的具体指标(如准确率、精确率、召回率等)可以作为基准,用于评估新模型的性能。如果你的新模型在这些指标上超越了BERT,那么你的研究就具有实际意义。
SOTA(State of the Art,最先进)
定义:SOTA是指在某个特定任务或领域中,当前已知的最佳性能或最先进的模型或算法。SOTA模型通常代表了该领域的最新进展和技术水平。
示例:在NLP任务中,BERT模型在多个任务上达到了SOTA性能,成为后续研究的重要参考。
神经网络量化(Neural Network Quantization)
定义:
旨在通过减少神经网络中权重和激活值的表示精度来降低计算复杂度和存储需求。量化通常涉及将浮点数(如32位浮点数)转换为较低精度的整数(如8位整数),从而减少模型的存储空间和计算开销。
主要目标
减少存储空间:量化后的模型占用更少的存储空间,便于在资源受限的设备(如移动设备、嵌入式系统)上部署。
降低计算复杂度:量化后的模型在计算时使用更少的位数,从而减少计算开销,提高推理速度。
加速推理:量化可以利用硬件加速器(如GPU、TPU)的低精度计算能力,进一步提高推理速度。
量化方法
线性量化:
均匀量化:将浮点数线性映射到整数范围。例如,将32位浮点数映射到8位整数。
非均匀量化:使用非线性映射,通常通过查找表(LUT)实现。
非线性量化:
对数量化:将浮点数映射到对数域,适用于权重分布不均匀的情况。
混合精度量化:在不同层或不同神经元中使用不同的量化精度。
训练感知量化(Quantization-Aware Training, QAT):
在训练过程中引入量化操作,使模型在训练时就适应量化后的表示。这样可以减少量化带来的精度损失。
对称量化(Symmetric Quantization) vs. 非对称量化(Asymmetric Quantization)
对称量化:量化范围以零为中心,即量化范围是对称的。例如,将32位浮点数映射到8位整数时,量化范围可能是[-128, 127]。
非对称量化:使用非均匀的量化范围来更好地适应数据的分布特性。量化范围不以零为中心,即量化范围是非对称的。例如,将32位浮点数映射到8位整数时,量化范围可能是[0, 255]或[-100, 155]。通常通过统计权重和激活值的分布来确定量化范围。
非对称量化可以更好地适应数据的实际分布,尤其是在数据分布偏斜的情况下。例如,如果数据主要集中在正数区域,非对称量化可以更有效地利用量化范围。通过更精确地匹配数据的分布,非对称量化可以减少量化误差,从而在一定程度上保持模型的精度。
量化过程
选择量化位数:决定量化后的位数,如8位、4位等。
确定量化范围:确定浮点数的量化范围,通常通过统计权重和激活值的分布来确定。
量化操作:将浮点数映射到整数范围,并存储量化后的权重和激活值。
反量化操作:在推理过程中,将量化后的整数反量化回浮点数进行计算。
应用场景
移动设备:在资源受限的移动设备上部署深度学习模型。
嵌入式系统:在嵌入式系统中实现高效的深度学习推理。
边缘计算:在边缘计算设备上进行实时推理。
示例
假设你有一个使用32位浮点数表示的卷积神经网络(CNN)模型。通过量化,你可以将权重和激活值转换为8位整数。这样,模型的存储空间可以减少到原来的1/4,计算复杂度也会显著降低。
神经网络量化步骤
选择量化位数:决定量化后的位数,如8位、4位等。
确定量化范围:确定浮点数的量化范围,通常通过统计权重和激活值的分布来确定。
量化操作:将浮点数映射到整数范围,并存储量化后的权重和激活值。
反量化操作:在推理过程中,将量化后的整数反量化回浮点数进行计算。
训练感知量化(可选):在训练过程中引入量化操作,使模型在训练时就适应量化后的表示。
大模型量化(Large Model Quantization)
是指对大规模深度学习模型进行量化处理,以减少模型的存储空间和计算复杂度。随着深度学习模型规模的不断增大,如BERT、GPT-3等,模型的参数量和计算量也急剧增加,这给模型的存储、推理和部署带来了巨大的挑战。大模型量化旨在通过降低模型的表示精度,来缓解这些挑战。
大模型的特点
参数量巨大:大模型通常包含数十亿甚至数千亿个参数。
计算复杂度高:大模型的推理和训练需要大量的计算资源。
存储需求大:大模型的存储需求巨大,尤其是在资源受限的设备上部署时。
大模型量化的目标
减少存储空间:通过量化减少模型的存储需求,使其更适合在资源受限的设备上部署。
降低计算复杂度:通过量化减少计算开销,提高推理速度。
保持模型精度:在量化过程中尽量减少模型精度的损失,确保量化后的模型仍然具有较高的性能。
大模型量化的方法
线性量化:
均匀量化:将浮点数线性映射到整数范围。例如,将32位浮点数映射到8位整数。
非均匀量化:使用非线性映射,通常通过查找表(LUT)实现。
非线性量化:
对数量化:将浮点数映射到对数域,适用于权重分布不均匀的情况。
混合精度量化:在不同层或不同神经元中使用不同的量化精度。
训练感知量化(Quantization-Aware Training, QAT):
在训练过程中引入量化操作,使模型在训练时就适应量化后的表示。这样可以减少量化带来的精度损失。
分层量化:
对模型的不同层采用不同的量化策略,以平衡精度和性能。例如,对计算密集的层使用较低的量化精度,对精度敏感的层使用较高的量化精度。
动态量化:
在推理过程中动态调整量化参数,以适应不同的输入数据。这种方法可以进一步减少量化带来的精度损失。
大模型量化的挑战
精度损失:大模型量化可能会导致较大的精度损失,尤其是在极端量化(如4位或更低)时。
复杂性:大模型量化需要仔细调整量化参数,以平衡精度和性能。
硬件支持:量化后的模型需要硬件支持低精度计算,否则可能无法充分发挥量化的优势。
应用场景
自然语言处理(NLP):如BERT、GPT等模型,其输入文本的长度和内容可能变化较大。
计算机视觉(CV):如目标检测模型,其输入图像的分辨率和内容可能变化较大。
推荐系统:大规模推荐模型,如DeepFM、Wide & Deep等,其输入特征的分布可能变化较大。
示例
假设你有一个使用32位浮点数表示的BERT模型,参数量达到数十亿。通过量化,你可以将权重和激活值转换为8位整数。这样,模型的存储空间可以减少到原来的1/4,计算复杂度也会显著降低。
大模型量化步骤
选择量化位数:决定量化后的位数,如8位、4位等。
确定量化范围:确定浮点数的量化范围,通常通过统计权重和激活值的分布来确定。
量化操作:将浮点数映射到整数范围,并存储量化后的权重和激活值。
反量化操作:在推理过程中,将量化后的整数反量化回浮点数进行计算。
训练感知量化(可选):在训练过程中引入量化操作,使模型在训练时就适应量化后的表示。
分层量化:对模型的不同层采用不同的量化策略,以平衡精度和性能。
动态量化(可选):在推理过程中动态调整量化参数,以适应不同的输入数据