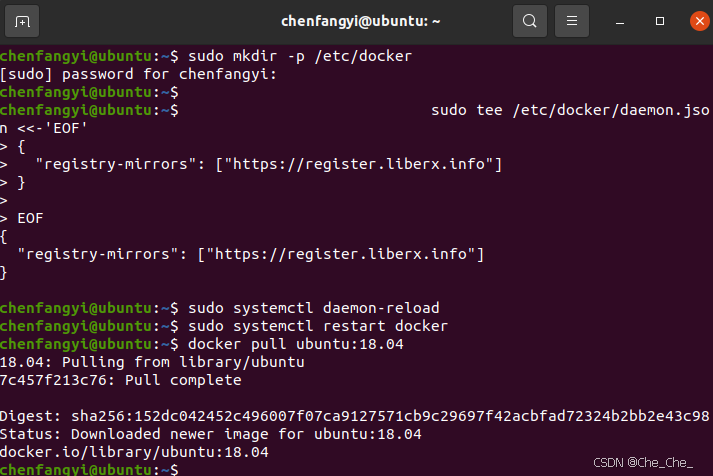
模板

package base;

public class Bsearch {
    public int binary_search1(int l, int r){
        while (l<r){
            int mid = (l+r+1)>>1;
            if(check(mid)) l=mid;
            else r = mid-1;
        }
        return l;

    }
    public int binary_search2(int l, int r){
        while (l<r){
            int mid = (l+r)>>1;
            if (check(mid)) r = mid;
            else l=mid+1;
        }
        return l;
    }
    public boolean check(int mid){

        return false;
    }
}

例题：

package test;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Test1 {
    public static void main(String[] args){
        BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
        try{
            System.out.println("输入数组长度:");
            int n = Integer.parseInt(bf.readLine());
            //定义数组
            int a[] = new int[n];
            for(int i = 0;i<n;i++){
                System.out.println("在数组中添加第"+(i+1)+"个数据:");
                a[i] = Integer.parseInt(bf.readLine());
            }
            //定义查询个数
            System.out.println("输入要查询元素的个数:");
            int q = Integer.parseInt(bf.readLine());
            //开始查找
            while(q-->0){
                System.out.println("输入要查询元素值:");
                int x = Integer.parseInt(bf.readLine());
                binary_search(n,a,x);
            }
        }catch(IOException e){
            e.printStackTrace();
        }
    }
    /*
    n:数组长度
    a[]:数组
    x：要查询的数x
    */
    public static void binary_search(int n,int[] a,int x){
        //定义指针
        int l = 0,r = n-1;
        while(l<r){
            //确定左边界
            int mid = (l+r)>>1;
            if(a[mid]>=x) r=mid;
            else l=mid+1;
        }
        if(a[l]!=x){
            System.out.println("-1 -1");
            return;
        }
        else System.out.print(l+" ");

        //确定右边界
        l = 0;
        r = n-1;

        while(l<r){
            int mid = (l+r+1)>>1;
            if(a[mid]<=x) l = mid;
            else r=mid-1;
        }
        System.out.println(l);
    }

}