计数排序

顾名思义：统计每个数据出现的次数。

算法思想

我们根据《算法导论》中给出对于计数排序的讨论：

对每一个输入元素 x, 确定小于 x 的元素个数。利用这一信息，就可以直接把 x 放到它在输出数组中的位置上了。例如，如果有 17 个元素小于 x , 则 x 就应该在第18个输出位置上。当有几个元素相同时，这一方案要略做修改。因为不能把它们放在同一个输出位置上。

它的工作过程分为三个步骤：

1. 计算每个数出现了几次；
2. 求出每个数出现次数的 前缀和；
3. 利用出现次数的前缀和，从右至左计算每个数的排名。

图解

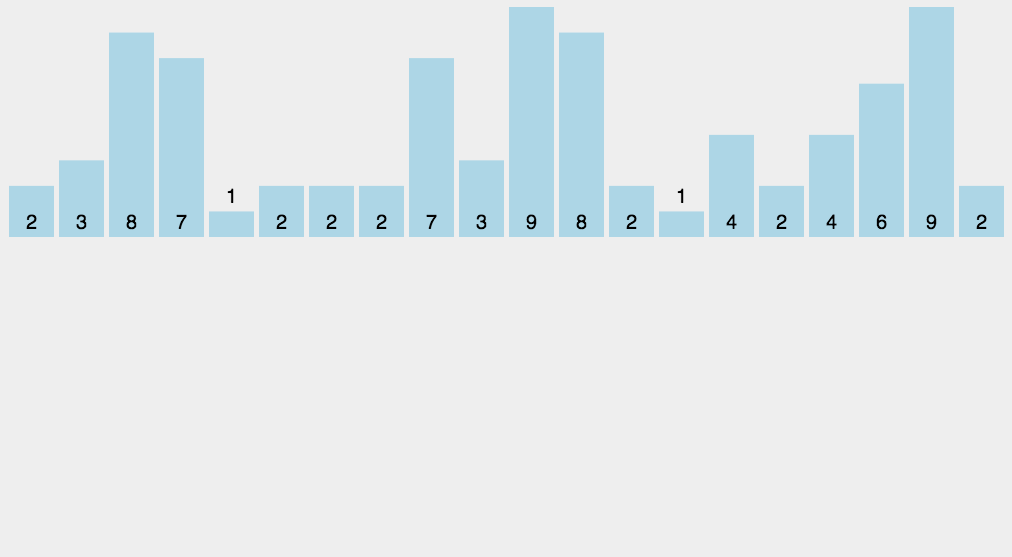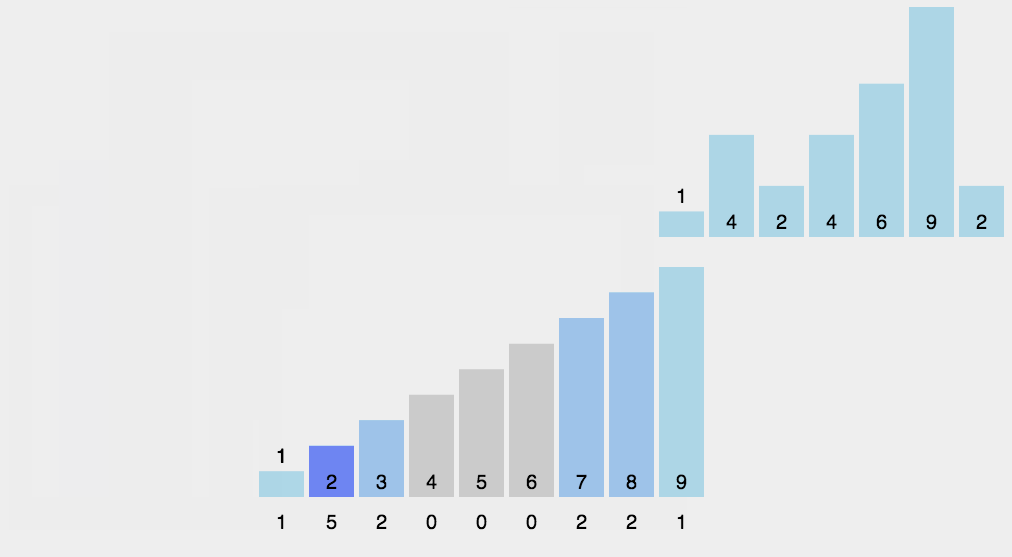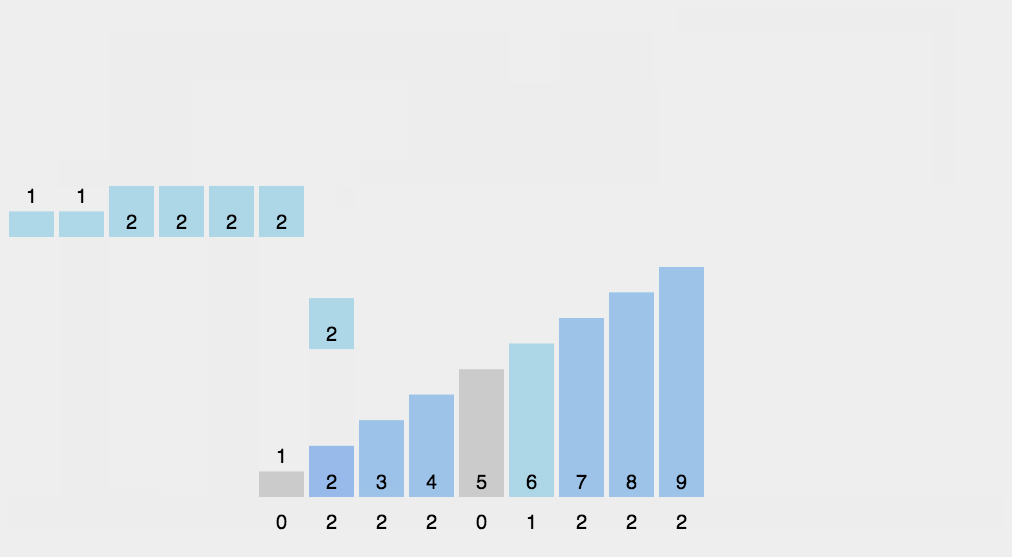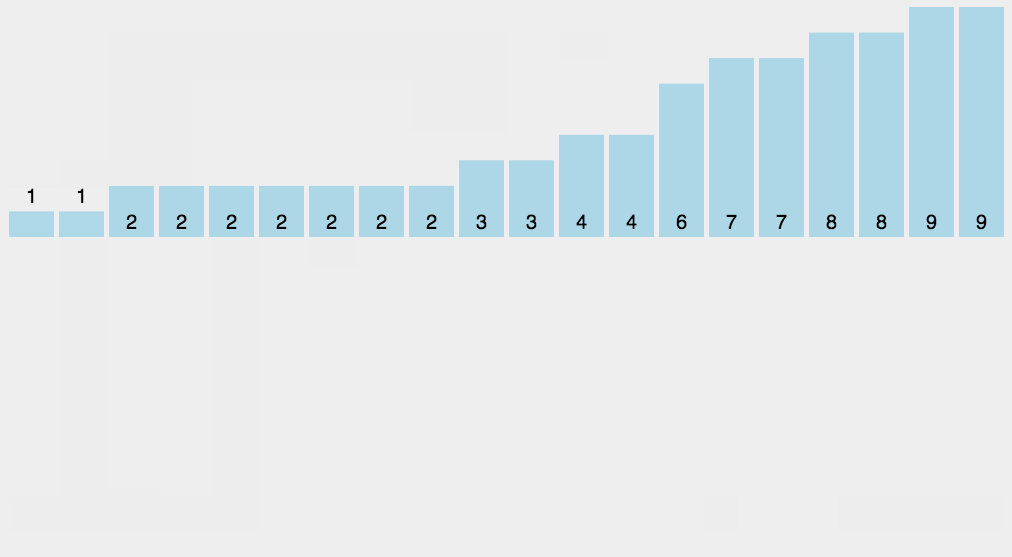
C语言代码分析

#define CRT_SECURE_NO_WARNINGS 1
//计数排序
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

void CountingSort(int arr[], int size)
{
	//找到数组中的最大值和最小值

	int max = arr[0];
	int min = arr[0];
	for (int i = 1; i < size; i++)//进行
	{
		if (arr[i] > max)//如果元素大于此时的最大值，则更新最大值
			max = arr[i];
		if (arr[i] < min)//如果元素小于此时的最小值，则更新最小值
			min = arr[i];
	}

	//创建计数数组，并初始化为0
	int range = max - min - 1;
	int* count = (int*)calloc(range, sizeof(int));

	//统计每个元素的出现次数
	for (int i = 1; i < size; i++)
	{
		count[arr[i] - min]++;//将元素的值作为下标，出现的次数作为值
	}

	//进行累加操作
	for (int i = 1; i < range; i++)
	{
		count[i] += count[i - 1];
	}

	//创建输出数组，并将元素按照排序结果依次放入
	int* output = (int*)malloc(size * sizeof(int));
	for (int i = size - 1; i >= 0; i--)
	{
		output[count[arr[i] - min] - 1] = arr[i];//将元素放入输出数组中
		count[arr[i] - min]--;//将元素的出现次数减1,符合C语言下标规则
	}

	//将排序结果放回原数组
	for (int i = 0; i < size; i++)
	{
		arr[i] = output[i];
	}

	free(count);
	free(output);
}

时间复杂度

我们发现这种算法实际上并没有进行比较——它是一个非比较排序算法。它主要进行的是一个分类的操作，将相同的数分在一类，在进行完分类后，再针对分类出来的代表数进行整体排序。但实际上这样的排序会有一个缺陷——如果相同的数过少，或者说整个数据组的同一性过小，那么实际上分类过程的意义也就会随之变小——从而还是主要依靠排序来进行算法的完成。这里我们就会谈及计数排序的局限性——它适用于范围集中且范围不大的整形数组排序。

计数排序的下界优于O（nlogn），因为它并不是一个比较排序算法。事实上，它的代码中完全没有输人元素之间的比较操作。相反，计数排序是使用输人元素的实际值来确定其在数组中的位置。当我们脱离了比较排序模型的时候，**O（nlogn）**这一下界就不再适用了。

我们一般根据数组的范围来判断其时间复杂度，为此我们可以给出大致的复杂度：

O(n+w)，其中w代表待排序数据的值域大小。

稳定性

计数排序的一个重要性质就是它是稳定的：具有相同值的元素在输出数组中的相对次序与它们在输人数组中的相对次序相同。也就是说，对两个相同的数来说，在输入数组中先出现的数，在输出数组中也位于前面。

计数排序的稳定性很重要的另一个原因是：计数排序经常会被用作基数排序算法的一个子过程。我们将在下一节中看到，为了使基数排序正确运行，计数排序必须是稳定的。