原文信息(包括题目、发表期刊、原文链接等):Learning to Warm-Start Fixed-Point Optimization Algorithms
原文作者:Rajiv Sambharya, Georgina Hall, Brandon Amos, and Bartolomeo Stellato
论文解读者:陈宇文
编者按:
这篇论文《Learning to Warm-Start Fixed-Point Optimization Algorithms》提出了一种利用机器学习技术对不动点优化算法进行热启动的框架。不动点问题广泛存在于控制、机器学习、运筹学和工程学等领域,这些问题通常采用迭代法来求解。然而,传统的不动点迭代算法由于收敛速度慢,往往需要大量计算资源。为了提升这些算法的效率,该论文引入了一种基于神经网络的热启动方法,旨在降低初始解的误差,从而减少迭代次数来达到加快求解速度的目的。
一、背景与动机
不动点问题的形式可以表达为“找到一个点 z z z,使得 z = T θ ( z ) z = T_\theta(z) z=Tθ(z)”,其中 T θ T_{\theta} Tθ 是定义问题的不动点算子。许多优化算法都可以归结为这种不动点迭代,例如梯度下降法、邻近梯度下降法、交替方向乘子法(ADMM)等。在实际应用中,不动点问题往往需要多次求解,每次求解的参数 θ \theta θ可能不同,但问题结构相似。这种情形常见于控制系统、图像处理、最优控制等领域。
尽管现有的加速技术如安德森加速法在某些情况下表现良好,但这些方法往往缺乏通用性和鲁棒性。另一方面,近年来兴起的优化学习方法通过从历史数据中学习参数结构来改进求解策略,但这些方法大多没有保证收敛性,也缺乏泛化能力。在此背景下,该论文提出了:
- 一种新的热启动框架,通过机器学习技术直接预测高质量的初始点,使得后续的迭代过程更加高效;
- 对于神经网络输出层的两种不同的损失函数。
二、框架设计
论文提出的框架由两个主要模块组成:神经网络和不动点迭代模块。神经网络的作用是将问题的参数
θ
\theta
θ映射到一个热启动点,这个点作为不动点算法的初始值。神经网络的结构采用了多层感知器(MLP),使用ReLU作为激活函数,并通过标准的随机梯度下降法(SGD)进行训练。随后,通过一个预定义的不动点迭代步骤数
k
k
k,将热启动点进一步迭代至接近最终解。不动点迭代的通用形式为
z
i
+
1
=
T
θ
(
z
i
)
z^{i+1} = T_\theta(z^i)
zi+1=Tθ(zi)
其中
T
θ
T_\theta
Tθ 是依赖于问题参数的不动点算子,
θ
∈
Θ
\theta \in \Theta
θ∈Θ是问题的参数。
该框架的一个显著优点是灵活性:神经网络预测输出后仍然执行 k k k次迭代。这种设计大大增强了模型在实际应用中的适应能力,使得模型实际加速效果更好。
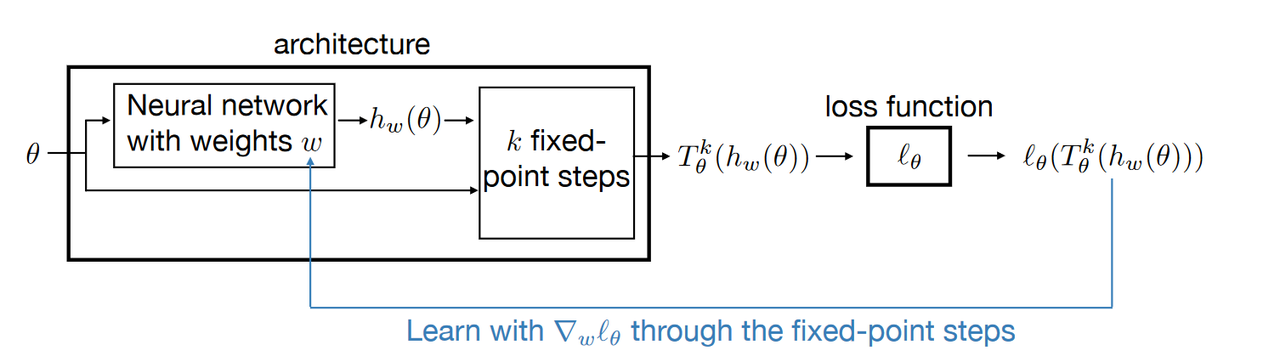
图1:不动点热启动方法的学习框架
对于输入
θ
\theta
θ,
L
L
L层的神经网络的预测为
h
w
(
θ
)
=
W
L
ϕ
(
W
L
−
1
ϕ
(
…
ϕ
(
W
1
θ
)
)
)
h_w(\theta) = W_L \phi(W_{L-1}\phi(\dots\phi(W_1 \theta)))
hw(θ)=WLϕ(WL−1ϕ(…ϕ(W1θ)))
为了保证初始值效果不是太差,
h
w
(
θ
)
h_w(\theta)
hw(θ) 还通过了
k
k
k次非扩张不动点迭代保证误差足够小,即输出
T
θ
k
(
h
w
(
θ
)
)
T_{\theta}^k(h_w(\theta))
Tθk(hw(θ))。
三、损失函数与优化目标
为训练神经网络,论文针对输出
T
θ
k
(
h
w
(
θ
)
)
T_{\theta}^k(h_w(\theta))
Tθk(hw(θ))设计了两种损失函数:不动点残差损失和回归损失。不动点残差损失
ℓ
θ
fp
(
z
)
=
∥
T
θ
(
z
)
−
z
∥
2
\ell^{\text{fp}}_\theta(z) = \|T_\theta(z) - z\|_2
ℓθfp(z)=∥Tθ(z)−z∥2
直接衡量迭代结果与不动点的收敛程度。这一指标反映了迭代结果距离收敛点的程度。而回归损失
ℓ
θ
reg
(
z
)
=
∥
z
−
z
⋆
(
θ
)
∥
2
\ell^{\text{reg}}_\theta(z) = \|z - z^\star(\theta)\|_2
ℓθreg(z)=∥z−z⋆(θ)∥2
则是惩罚最终输出与一个已知的目标解之间的距离,这里的目标解
z
⋆
(
θ
)
z^\star(\theta)
z⋆(θ) 是不动点算子的一个已知解。这种设计的目的是使得神经网络能够在具体的迭代步数下,生成更优的初始点,从而提升求解的效率。
两种损失函数适用于不同的条件(见论文5.2节):
- 固定点残差损失更适用于没有目标解或目标解难以计算的情况,且与最终评价指标一致,简单易用,但仅依赖局部信息。
- 回归损失提供了利用全局信息的优势,可以更好地引导热启动点向全局最优 z ⋆ ( θ ) z^\star(\theta) z⋆(θ)靠近,适合有明确目标解的场景,但需要事先计算这些目标解。
四、理论分析与泛化保证
为了证明该框架的有效性和可靠性,论文采用了PAC-Bayes理论,这是一种用于分析学习算法泛化能力的统计学习理论。PAC-Bayes理论特别适合处理随机化预测器,这些预测器通过在一组基本预测器中根据特定的概率分布进行采样来做出预测。在本文的框架中,基本预测器是由神经网络权重 w ∈ W w \in \mathcal W w∈W和随机扰动 u u u 定义的。
4.1 PAC-Bayes框架
PAC-Bayes框架主要用于提供在未知数据上的风险界限。对于一个由权重 w w w 参数化的神经网络,假设其权重经过某种分布的扰动 w + u w + u w+u,论文证明了期望风险的上界可以用经验风险加上一项与KL散度相关的罚项来表示。具体来说,对于给定的固定点迭代步数 t t t,我们定义评价风险(Risk)和经验风险(Empirical Risk)如下:
- 风险 R t ( w ) R^t(w) Rt(w):表示在未知数据分布 Q Q Q 下,神经网络在 t t t 次固定点迭代后的平均固定点残差。其定义为:
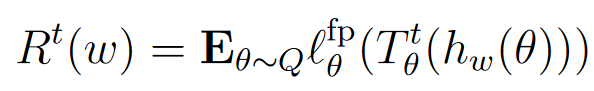
- 经验风险 R ^ t ( w ) \hat{R}^t(w) R^t(w):表示在训练数据上计算得到的经验平均固定点残差。假设我们有 N N N 个训练样本,则定义为:
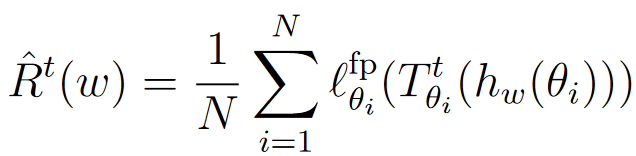
考虑误差扰动的影响,我们定义边缘不动点残差 g γ , θ t ( z ) g^t_{\gamma,\theta}(z) gγ,θt(z)来刻画在 γ \gamma γ扰动下的残差:
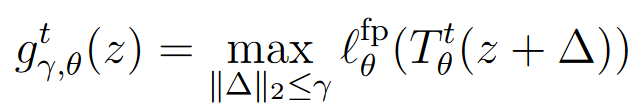
对应的风险和经验风险就变成
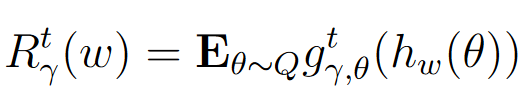
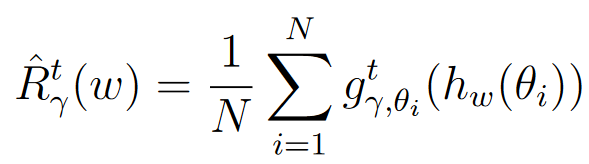
论文使用PAC-Bayes界限来描述在未知数据上实际风险 R γ t ( w ) R_{\gamma}^t(w) Rγt(w)与经验风险 R ^ γ t ( w ) \hat{R}_{\gamma}^t(w) R^γt(w)在一定扰动 u u u下的关系。PAC-Bayes定理表明,在至少概率 1 − δ 1-\delta 1−δ的条件下,实际风险 E u [ R γ t ( w + u ) ] \mathbf{E}_u[R_{\gamma}^t(w+u)] Eu[Rγt(w+u)]的上界可以表示为,
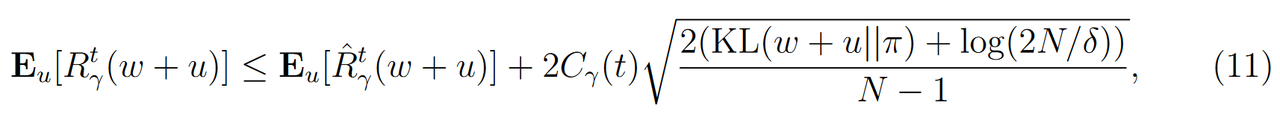
其中:
- KL ( p ∥ π ) \text{KL}(p \| \pi) KL(p∥π):表示后验分布 p p p 和先验分布 π \pi π 之间的KL散度,这一项衡量了学习后的权重分布相对于先验分布的变化程度。
- C γ ( t ) C_\gamma(t) Cγ(t):是用于限制 t t t次迭代后不动点残差的上界值,即:
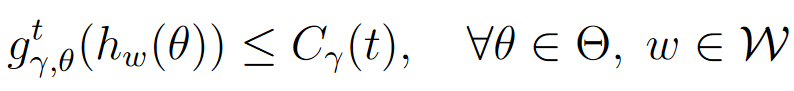
- δ \delta δ:是一个置信度参数,表示泛化界限在 1 − δ 1 - \delta 1−δ 的概率下成立。
4.2 算子类型与界限推导
基于公式(11),文中4.2节给出了一个通用的上界定理:
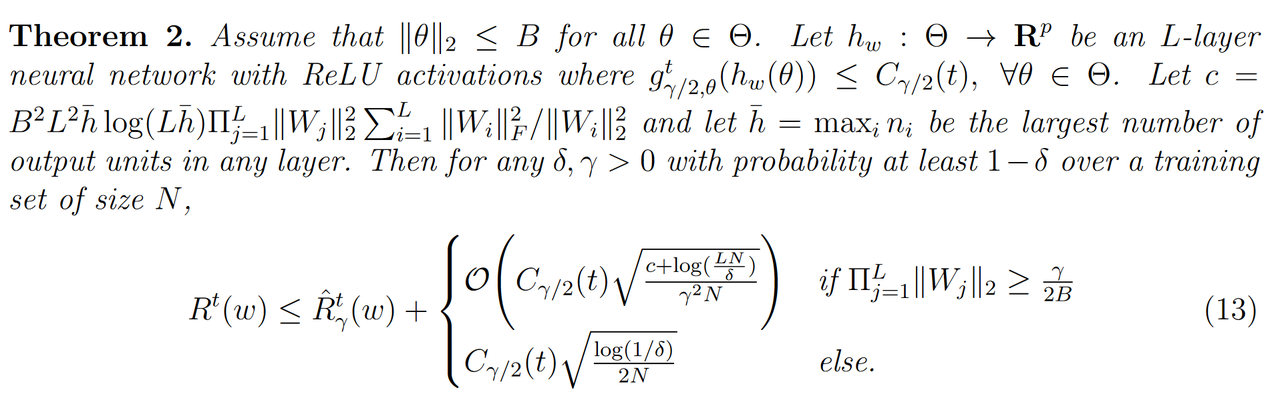
这个定理表明随着训练数据数量 N N N的上升,右边上界第二个部分是会逐渐递减的,同时右边第二个部分 C γ / 2 ( t ) C_{\gamma/2}(t) Cγ/2(t) 与不动点迭代次数 t t t也有关。论文在4.3节中进一步将确定三种常见的固定点算子类型的泛化上界 C γ / 2 ( t ) C_{\gamma/2}(t) Cγ/2(t):收缩型算子、线性收敛型算子和平均算子:
-
收缩型算子( β \beta β-contractive Operators):对于收缩系数 β ∈ ( 0 , 1 ) \beta \in (0, 1) β∈(0,1) 的算子,假设满足:
∥ T θ ( x ) − T θ ( y ) ∥ 2 ≤ β ∥ x − y ∥ 2 ∀ x , y ∈ dom T \| T_\theta(x) - T_\theta(y) \|_2 \leq \beta \| x - y \|_2 \quad \forall x, y \in \text{dom} \, T ∥Tθ(x)−Tθ(y)∥2≤β∥x−y∥2∀x,y∈domT
PAC-Bayes界限中的残差上界 C γ / 2 ( t ) ≤ 2 β t ( D + γ / 2 ) C_{\gamma/2}(t) \le 2\beta^t(D + \gamma/2) Cγ/2(t)≤2βt(D+γ/2),其中 D D D 是神经网络输出与固定点集的距离。 -
线性收敛型算子( β \beta β-linearly Convergent Operators):对于线性收敛算子,定义满足:
dist fix T ( T θ ( x ) ) ≤ β dist fix T ( x ) , β ∈ [ 0 , 1 ) \text{dist}_{\text{fix} \, T}(T_\theta(x)) \leq \beta \, \text{dist}_{\text{fix} \, T}(x), \beta \in [0, 1) distfixT(Tθ(x))≤βdistfixT(x),β∈[0,1)
在这种情况下,残差上界 C γ / 2 ( t ) C_{\gamma/2}(t) Cγ/2(t)可以通过递归关系推导得到为 C γ / 2 ( t ) ≤ 2 β t ( D + γ / 2 ) C_{\gamma/2}(t) \le 2\beta^t(D + \gamma/2) Cγ/2(t)≤2βt(D+γ/2)。 -
平均算子(Averaged Operators):对于一个 α \alpha α-平均的算子 T = ( 1 − α ) I + α R T = (1 - \alpha) I + \alpha R T=(1−α)I+αR,其中 R R R 是非扩张算子。在此情况下,残差上界 C γ / 2 ( t ) ≤ α ( 1 − α ) ( t + 1 ) ( D + γ ) C_{\gamma/2}(t) \le \sqrt{\frac{\alpha}{(1-\alpha)(t+1)}(D+\gamma)} Cγ/2(t)≤(1−α)(t+1)α(D+γ)(见文中引理7的分析)。
这一界限揭示了平均算子的残差收敛特性,其界限会随着不动点迭代次数 t t t 实现次线性收敛。
五、实验验证与泛化效果
在实际的实验中,研究者对多个固定点算子进行了测试,评估了这些泛化界限在未见数据上的有效性。我们选取其中一组在鲁棒卡尔曼滤波问题上的实验结果。其中,$ x_t \in \mathbb{R}^{n_x} $ 是状态变量,$ y_t \in \mathbb{R}^{n_o} $ 是观测,$ w_t \in \mathbb{R}^{n_u} $ 是输入变量,$ v_t \in \mathbb{R}^{n_o} $ 是观测的扰动变量。矩阵 $ A \in \mathbb{R}^{n_x \times n_x}, B \in \mathbb{R}^{n_x \times n_u}, $ 和 $ C \in \mathbb{R}^{n_o \times n_x} $ 描述了系统的动态。案例的目标是从噪声观测 $ y_t $ 中恢复状态 $ x_t $。为此,我们求解如下问题:
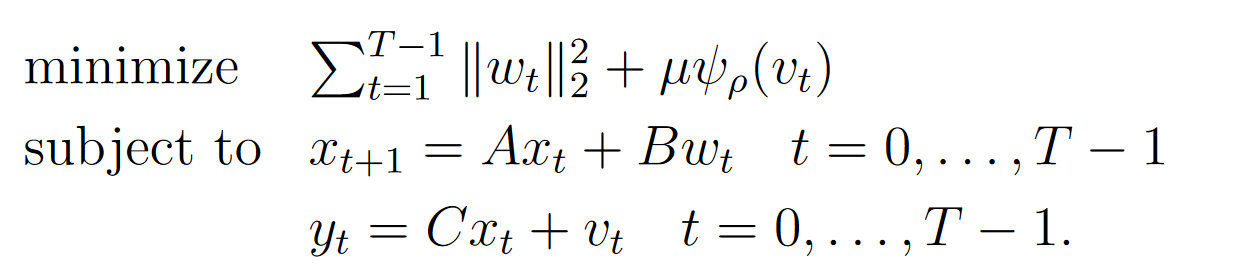
其中 ψ ρ ( x ) \psi_\rho(x) ψρ(x)是Huber惩罚函数。$ \mu > 0$ 是该惩罚项的权重。决策变量是 $ x_t 、 、 、 w_t $ 和 $ v_t $。参数是观测的 $ y_t $,即 $ \theta = (y_0, \ldots, y_{T-1}) $。实验结果见下图,其中评估了使用不同初始化策略(如冷启动、最近邻热启动以及本文学习不同k值的热启动策略)的迭代效率。
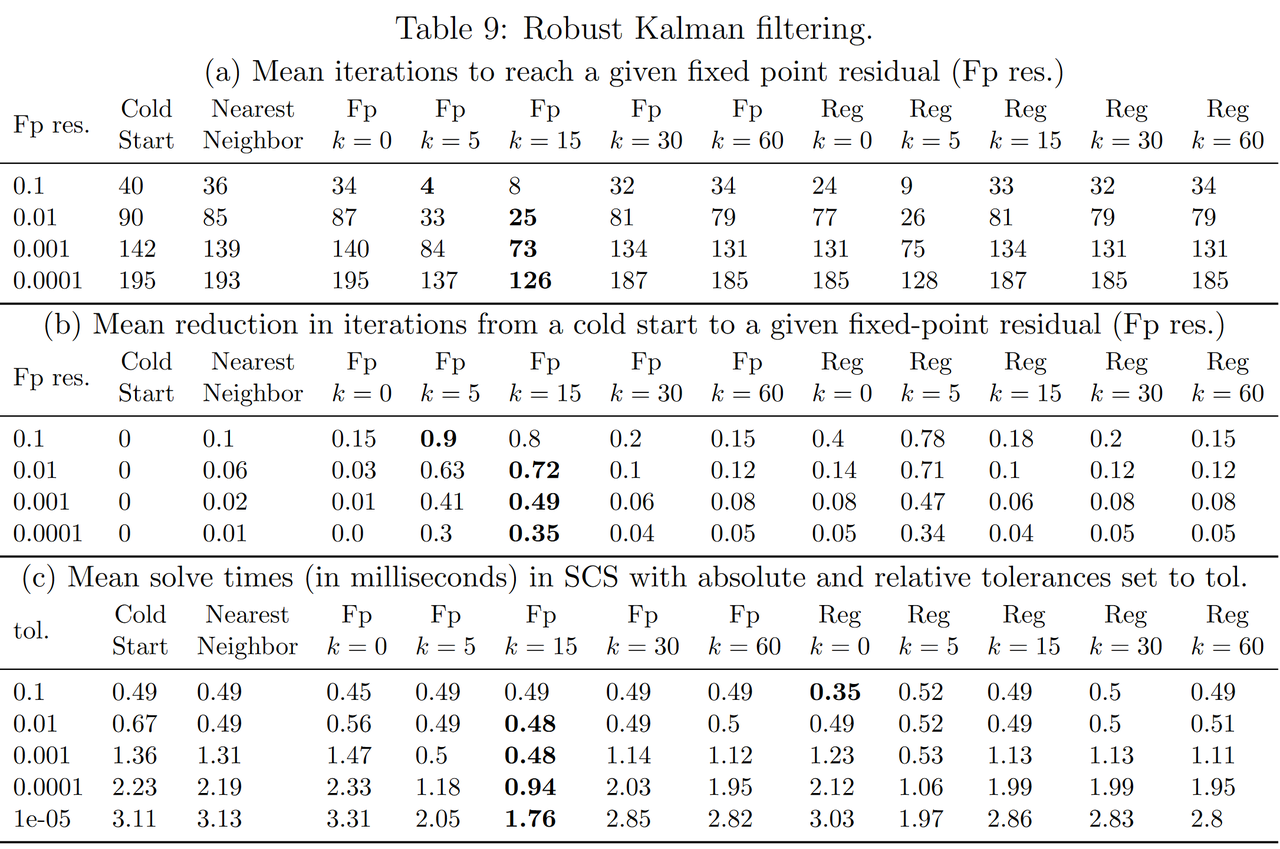
可以看到,采用了学习算法的热启动方法在 k > 0 k > 0 k>0时可以显著提升热启动的性能(对比 k = 0 k=0 k=0情况)。但是不同于PAC理论证明的上界单调递减, k k k值增大也有可能造成过拟合,反而导致热启动效果变差。此外,当精度增高时,热启动的加速效果也是在逐渐下降。