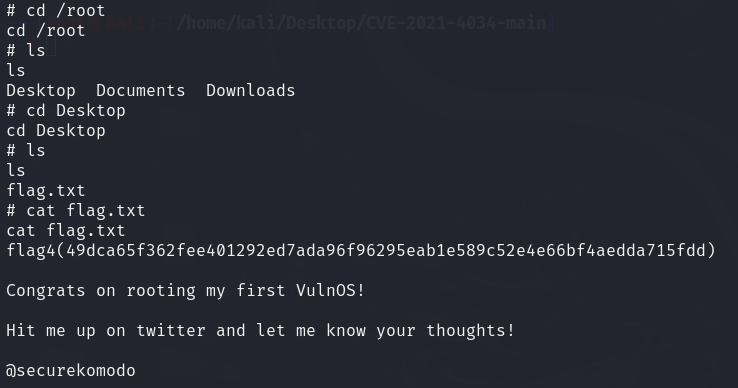
题目

思路

• $gcd(x,y)=px,y\in [1,N]$
  • 转换为 $gcd(\frac{x}{p},\frac{y}{p})=1\frac{x}{p},\frac{y}{p}\in [1,\frac{N}{p}]$ 注意这里，确定了p之后才确定了取值集合（不同p值下的取值集合，哪怕元素值一样意义也不一样，因为对应的p值不一样，最终还原出的x不一样，最开头的gcd值p也不一样），这个区间内的每个整数都要欧拉函数化，为下文的前缀和埋下伏笔
  • 处理欧拉数组 $\phi [i]$，这里 $\phi [1]\ne 1$，下文单独拿出来算
  • 分三种情况考虑 $\frac{x}{p}>\frac{y}{p}(\phi (\frac{x}{p}))$ 、$\frac{x}{p}<\frac{y}{p}(\phi (\frac{y}{p}))$、$\frac{x}{p}=\frac{y}{p}=1(1)$
  • 构造 $s[t]={\sum }_{i=1}^t\phi [i]$
  • 每个 $p$ 下的个数表达式为 $s[\frac{n}{p}]\cdot 2+1$
  • 计算
    • 遍历 $pp\le n$
    • $res=res+s[\frac{n}{p}]\cdot 2+1$

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;

const int N = 1e7+10;
int primes[N], cnt;
bool st[N];
int phi[N];
LL s[N];
void init(int n)
{
    for(int i = 2; i <= n; i++)
    {
        if(!st[i])
        {
            primes[++cnt] = i;
            phi[i] = i-1;
        }
        for(int j = 1; primes[j] * i <= n; j++)
        {
            st[primes[j]*i] = true;
            if(i % primes[j] == 0)
            {
                phi[primes[j]*i] = phi[i] * primes[j];
                break;
            }
            phi[primes[j]*i] = phi[i] * (primes[j] - 1);
        }
    }
    
    for(int i = 1; i <= n; i++) s[i] = s[i-1] + phi[i];
}
int main()
{
    int n;
    cin >> n;
    init(n);
    
    LL res = 0;
    for(int i = 1; i <= cnt; i++)
    {
        res += s[n/primes[i]] * 2 + 1;
    }
    
    cout << res;
    return 0;
}