一、X射线衍射分析简史

1895年X射线发现
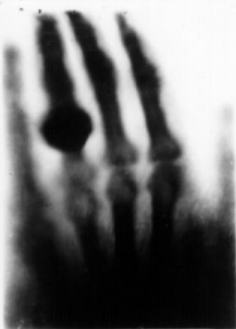
1896 年 2 月对骨折的观察:G.和 E. Frost是第一个使用 X 射线进行医疗用途
1897 年法国海关官员的行李扫描。
X射线衍射理论1
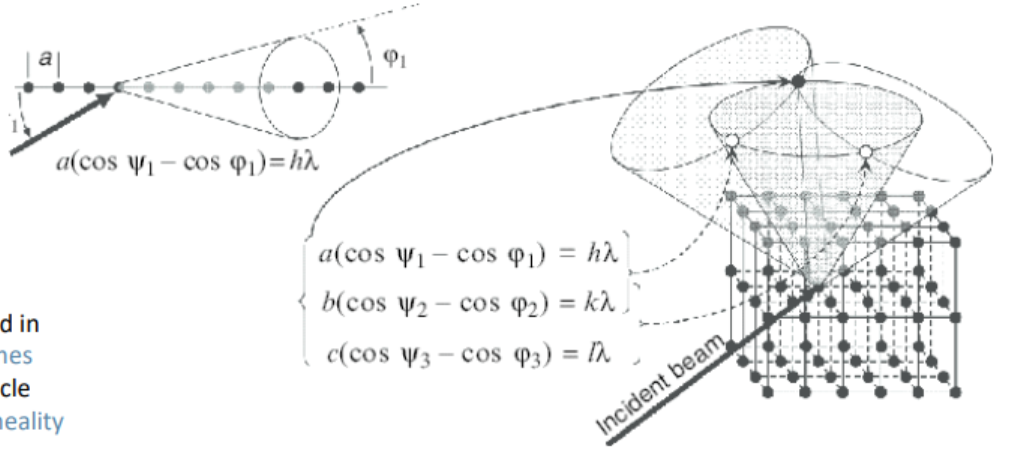
X射线衍射理论2
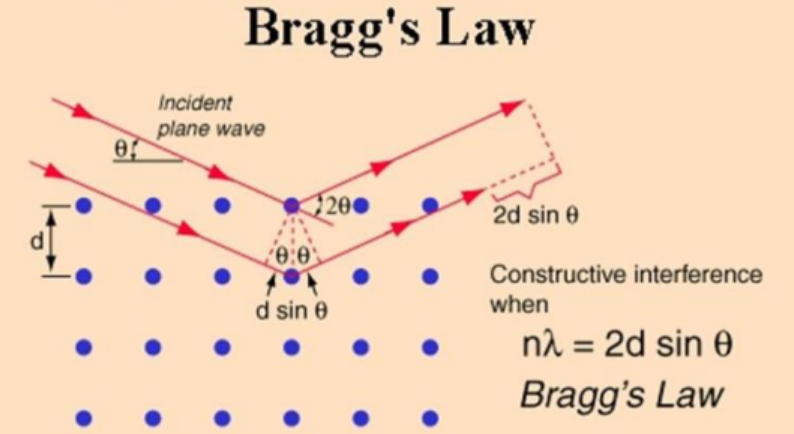
元素的特征X射线

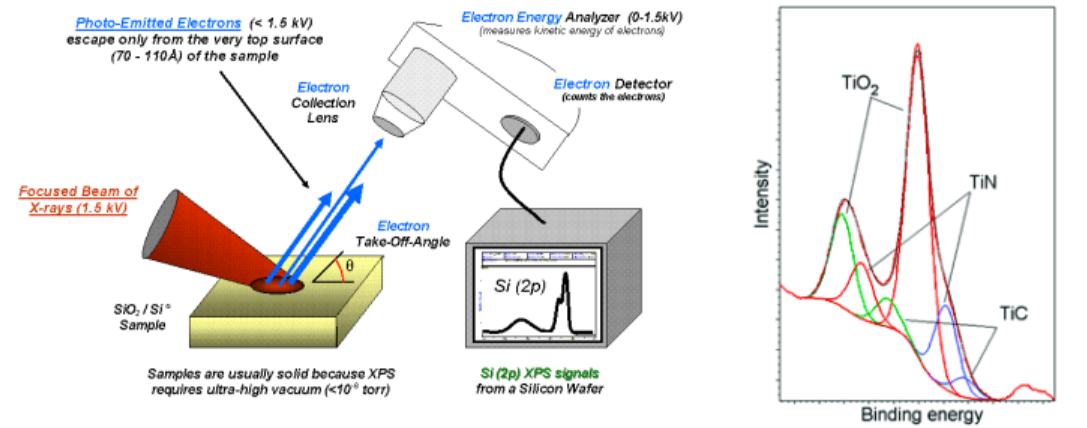
X射线光电子的应用
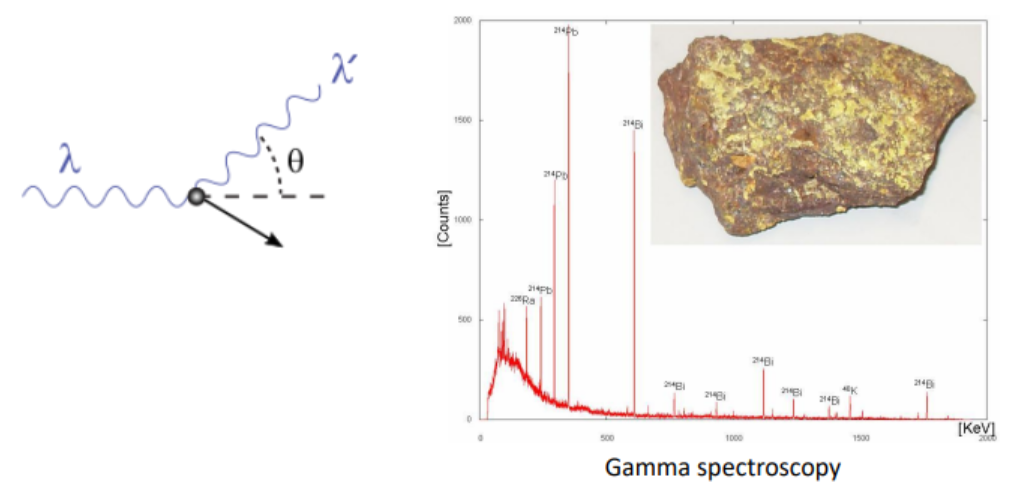
电磁波的粒子属性
X射线层析成像法
X-ray Computed Tomography X 射线计算机断层扫描 (CT)
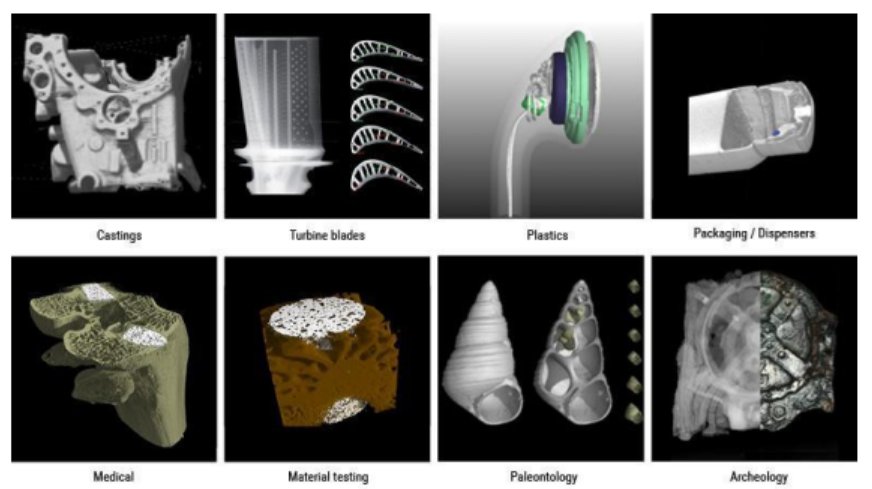
X 射线衍射 (XRD) 只是 X 射线在材料表征中的应用之一
二、X射线的本质和产生
1.X射线的本质
X射线是电磁波的一种。
**电磁波(Electromagnetic wave)**是由同相振荡且互相垂直的电场与磁场在空间中衍生发射的振荡粒子波,是以波动的形式传播的电磁场,具有波粒二象性,其粒子形态称为光子,电磁波与光子是根据实际研究的不同,其性质所体现出的两个侧面。电磁波是横波,由同相振荡且互相垂直的电场与磁场在空间中以波的形式移动,其传播方向垂直于电场与磁场构成的平面。电磁波在真空中速率固定,速度为光速。见麦克斯韦方程组。
在X射线衍射分析中,记录的是电场强度矢量所引起的物理效应,磁场强度矢量引起的效应不再提及。
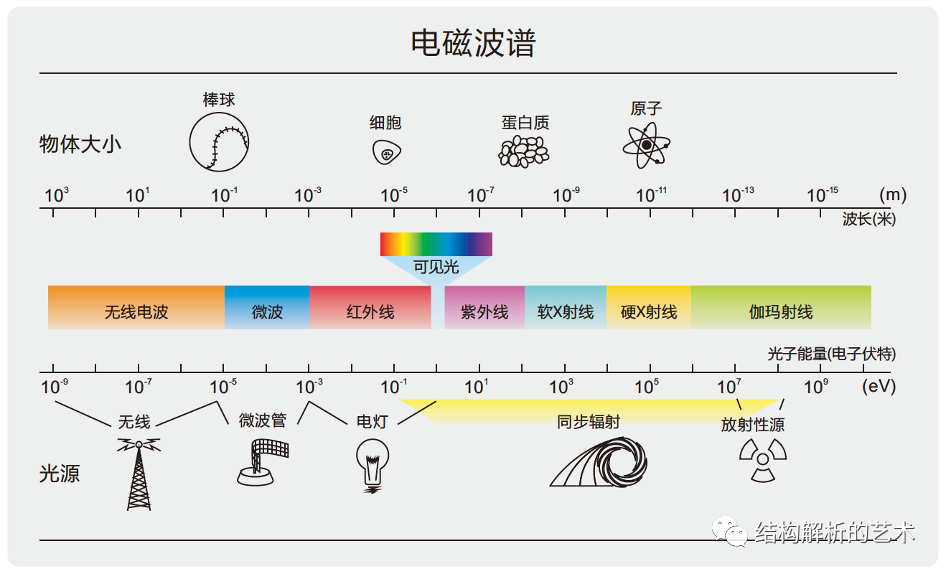
X射线是电磁波,具有波粒二象性。
1.波动性
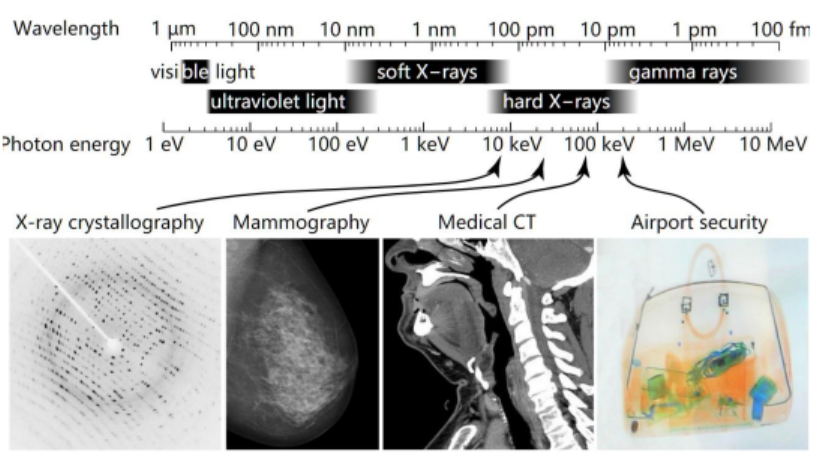
X射线对应波长为 1 0 − 12 10^{-12} 10−12~ 1 0 − 9 10^{-9} 10−9m,波长和紫外线和γ射线有一定交叠。
不同用途X射线波长不同,X射线波长越短,穿透材料的能力越强(衍射的能力越强)。
根据X射线波长不同分为:
- 硬X射线:
- 波长为0.25~0.05nm,用于晶体结构分析;
- 波长为0.1~0.005nm,用于金属无损检测
- 软X射线:波长为1~100nm,用于医学透视及安检
波动性表现:
-
连续、干涉和衍射(三角函数描述)
-
与物质相互作用:吸收和散射(统计学描述)
2.粒子性
描述X射线波动的物理量(频率
ν
\nu
ν、波长λ)与描述粒子特性光子能量E、动量P之间,遵循爱因斯坦关系式:
E
=
m
c
2
=
h
ν
=
h
c
/
λ
P
=
m
c
=
h
/
λ
=
h
ν
/
c
E=mc^2=h\nu=hc/\lambda\\ P=mc=h/\lambda=h\nu/c
E=mc2=hν=hc/λP=mc=h/λ=hν/c
2.X射线的产生
真空中高速运动的带电粒子撞击到任何物质时均可产生X射线。
产生X射线基本条件为:
- 产生自由电子
- 使电子做定向高速运动
- 在电子运动路径上设置突然减速的障碍物
产生X射线的设备——X射线管
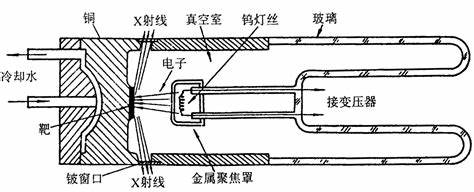
管内抽成真空,电子运行不受阻碍,使阴极发出电子在电场作用下到达阳极
阴极采用钨丝(耐高温,原子序数高更容易失去电子),通过电流加热,阴极表面原子的外层电子,受到一定的热能或电能的激励后,会越出轨道的束缚而成为自由电子。
阳极接地,用水冷却(和阳极靶相撞,产生热)。一般阳极靶采用导热性好、熔点高的材料制成,如Cu。
在靶上镀上一层过渡金属防止烧毁或者用转靶装置(靶面受到阴极电子束轰击的部位不断变换)
工作过程: X射线是由阴极加发射出(热)电子, 经高速电压加速,获得能量,运动速度很大, 这种高速电子去撞击阳极A,电子部分动能转变为X光能,以光子的形式表现出来。
三、特征X射线与连续X射线(Characteristic X-ray and Bremsstrahlung Continuum)
1.连续X射线
1.连续辐射和连续谱
连续辐射/韧致辐射:阴极射出的高速电子和靶材原子相撞,运动受阻而减速,其损失的动能以X射线光子的形式辐射出来。每次碰撞损失的动能不完全相等,因此辐射出的X射线光子的波长是按统计规律连续分布的。
X射线连续谱:大量电子冲击靶所辐射出的X射线光量子的波长,按照统计规律连续分布在一个较大的波长范围,所获得的强度。
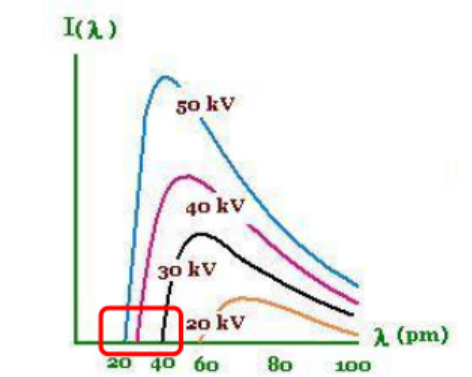
短波限:横轴右侧截距
2.短波限
在管电压V的作用下,电子到达阳极靶的动能为eV,如果电子动能全部转化成一个X光光子,则此光子具有最大的能量、频率和最短的波长,此时的波长为短波限: e V = h ν = h c λ 0 = > λ 0 = h c e V eV=h\nu=h\frac{c}{\lambda_0}=>\lambda_0=\frac{hc}{eV} eV=hν=hλ0c=>λ0=eVhc
代入各项常数,得: λ 0 = 12.40 V ( 1 0 − 10 m ) = 1.24 V ( n m ) \lambda_0=\frac{12.40}V(10^{-10}m)=\frac{1.24}V(nm) λ0=V12.40(10−10m)=V1.24(nm)
可知短波限只与管电压有关而与管电流和靶材的原子序数无关。 管电压越高,撞击越剧烈,高频无量子越多, 短波限和曲线峰值也左移。
3.连续X射线谱的强度
连续X射线谱的强度指的是曲线下包围的面积,实验得: I 连 = ∫ λ 0 ∞ I ( λ ) d λ = K 1 i Z V 2 I_{连}=\int_{\lambda_0}^{\infin}I(\lambda)d\lambda=K_1iZV^2 I连=∫λ0∞I(λ)dλ=K1iZV2
K 1 K_1 K1是常数 1.4 × 1 0 − 9 V − 1 1.4\times 10^{-9}V^{-1} 1.4×10−9V−1,i是管电流,Z是阳极靶材的原子序数,V是管电压。
- 管电压越高,相对强度越大,短波限越小
- 管电流越大,相对强度越大,短波限不变
- 靶材原子序数越高,相对强度越大,短波限不变

X射线管发射连续X射线的效率η: η = 连续 X 射线总强度 / X 射线管功率 = K 1 i Z V 2 / i V = K 1 Z V \eta=连续X射线总强度/X射线管功率=K_1iZV^2/iV=K_1ZV η=连续X射线总强度/X射线管功率=K1iZV2/iV=K1ZV
以钨(Z=74)阳极,管电压100kV为例,则 η ≈ 1 \eta\approx1% η≈1,可见,X射线管效率很低,绝大部分能量在撞击时转化为热能丧失,所以采取有效的冷却措施是必要的。
2.特征X射线
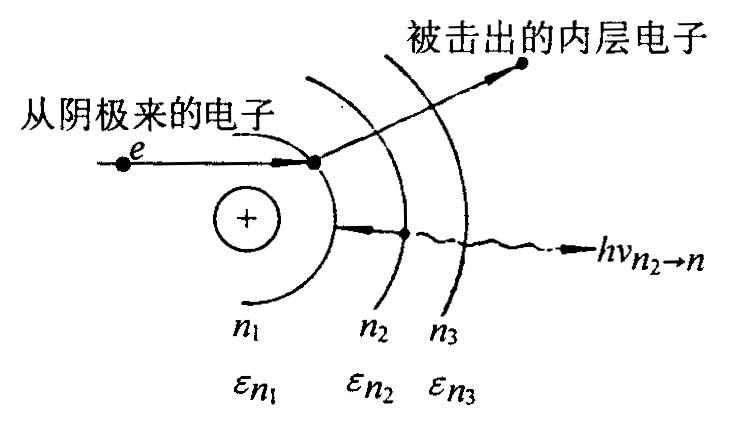
特征X射线:阴极射向阳极的电子具有足够大的动能时,把靶材原子的某些内层电子撞离产生空位,使原子处于不稳定高能激发态,于是,外层电子向内层跃迁填补空位,多余的能量以X射线光子的形式辐射出来。
特征辐射/标识辐射:选定阳极靶,其原子核外每层电子能量恒定,跃迁辐射出的光子波长也是若干个特征值,它们反映出原子的原子序数特征,和原子所处的物理、化学状态基本无关。故称这种辐射为特征辐射。
特征X谱线:X射线谱上,狭小而尖锐的、叠加于连续谱上的谱线,这些谱线对应的波长与管电压和电流无关,称为特征X谱线。
特征X射线频率
当电子从主量子数 n 2 n_2 n2跃迁到 n 1 n_1 n1时, h ν n 2 → n 1 = E n 2 − E n 1 = R h c ( Z − σ 2 ) ( 1 n 1 2 − 1 n 2 2 ) h\nu_{n_2\rightarrow n_1}=E_{n_2}-E_{n_1}=Rhc(Z-\sigma^2)(\frac1{n_1^2}-\frac1{n_2^2}) hνn2→n1=En2−En1=Rhc(Z−σ2)(n121−n221)
K系谱线:跃迁到K层空位所辐射的特征X射线,根据不同的壳层K、L、N、……,把K系谱线分为 K α , K β , . . . K_{\alpha},K_{\beta},... Kα,Kβ,...

特征X射线波长(莫塞莱定律)
希望得到单色的X射线。
已知== λ = c ν = > 1 λ = K 2 ( Z − σ ) \lambda=\frac c{\nu}=>\sqrt{\frac1{\lambda}}=K_2(Z-\sigma) λ=νc=>λ1=K2(Z−σ)==,这里的 K 2 K_2 K2是和n有关的常数,σ是屏蔽常数(和电子所在壳层位置有关)
莫塞莱定律是X射线荧光光谱和电子探针微区成分分析的理论基础。
特征X射线应用
1.特征X射线作为被收集的信号——能谱:一个元素有一组自己的特征谱线,根据特征谱线识别不同元素越靠近原子核,相邻能级间的能量差也越大; 同一电子层,靠外亚层的电子能量高,跃迁释放的波长短。
E K α > E L α > E M α E_{K\alpha}>E_{L\alpha}>E_{M\alpha} EKα>ELα>EMα
E K β > E K α > E L α E_{K\beta}>E_{K\alpha}>E_{L\alpha} EKβ>EKα>ELα

2.特征X射线作为发射的光源——XRD:作为单一波长的光源进入被测晶体
一般选择K系谱线作为晶体衍射所需射线,L和 M系能量较低,易被吸收。 阳极靶材一般选用Cr,Fe,Co,Cu, Mo等。
注意:在此应用中,单一波长X射线作为光源进入被检测的晶体,与晶体内的不同组晶面发生衍射。
四、X射线与物质的相互作用(X-ray’s Interaction with Matter)
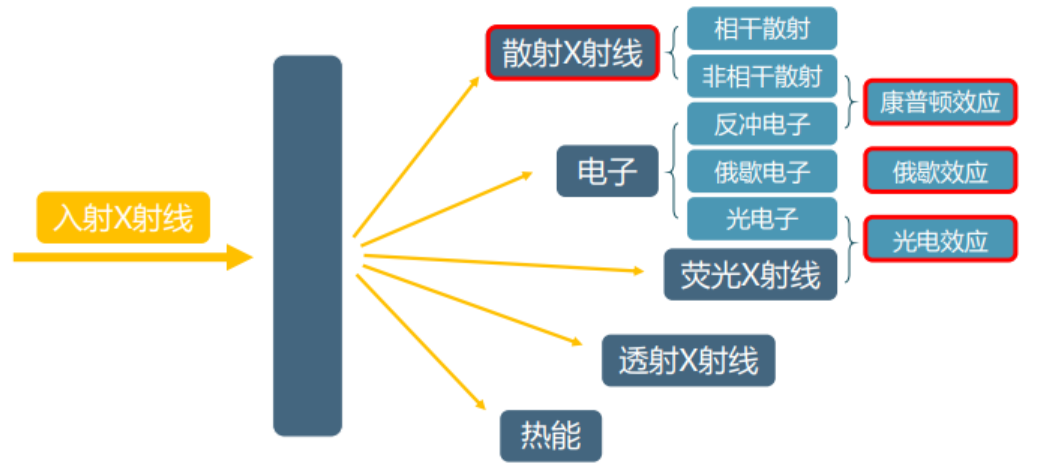
物质对X射线的吸收有两种方式:
- 原子对X射线的漫反射,形成漫反射的X射线四周发散,其能量只占吸收能量的一小部分。
- 电子在原子内迁移引起的,其能量主要包括光电子吸收、荧光X射线辐射、俄歇电子等能量以及热散能量,称为真吸收。
漫反射式吸收和真吸收构成了由质量吸收系数 μ m \mu_m μm表征的全吸收。
1.散射现象
物质对X射线的散射主要是电子和X射线交互作用的结果。
-
相干散射:射线与内层电子发生碰撞,能量没有失去,但方向发生变化,故频率和波长没有变化。——发生衍射的基础
-
非相干散射:射线与外层电子或价电子或金属晶体中的自由电子相碰撞时,电子被撞离电子带走部分能量,而成为了反冲电子。射线方向和波长都发生变化。
根据散射前后能量和动量守恒,推导出散射X射线的波长增大值: Δ λ = λ ′ − λ = h m e c ( 1 − c o s θ ) = λ e ( 1 − c o s θ ) = 0.00245 ( 1 − c o s θ ) = 2 λ e s i n 2 θ 2 ( n m ) \Delta\lambda=\lambda'-\lambda=\frac{h}{m_ec}(1-cos\theta)=\lambda_e(1-cos\theta)=0.00245(1-cos\theta)=2\lambda_esin^2\frac{\theta}2(nm) Δλ=λ′−λ=mech(1−cosθ)=λe(1−cosθ)=0.00245(1−cosθ)=2λesin22θ(nm)
各原子产生的X射线散射波散布空间各个方向,波长互不相同,也不存在确定的周相关系,互不干涉。
入射X射线波长越短,被照物质元素越轻,非相干散射越显著。

2.吸收现象

把非相干散射的X射线作为信号来收集,从而识别。
(1)X射线真吸收与衰减规律
X射线的吸收:X射线穿过被照物体,因为散射、光电效应、热损耗的影响,出现强度衰减。
衰减的程度和所经过物质的厚度成正比,也和入射X射线的强度和物质密度密切相关。
强度为 I 0 I_0 I0的入射线穿过厚度为 Δ x \Delta x Δx的物件后,强度衰减为I,则: I 0 − I I 0 = Δ I I 0 = − μ l Δ x \frac{I_0-I}{I_0}=\frac{\Delta I}{I_0}=-\mu_l\Delta x I0I0−I=I0ΔI=−μlΔx

这里的 μ l \mu_l μl是被照射物体的线吸收系数或衰减系数, c m − 1 cm^{-1} cm−1,相当于单位厚度物质对X射线的吸收。
当 Δ x \Delta x Δx很小时,上述式子近似等于 d I I = − μ l d x \frac{dI}{I}=-\mu_ldx IdI=−μldx
μ l \mu_l μl不仅和原子序数Z、X射线的波长有关,还和物质的密度有关。为了去掉密度对吸收系数的影响,用 μ m \mu_m μm代替 μ l \mu_l μl: μ l = μ m ρ \mu_l=\mu_m\rho μl=μmρ, μ m \mu_m μm为质量吸收系数,和物质密度无关,表示单位质量物质对X射线的吸收程度。
对 d I I = − μ l d x \frac{dI}{I}=-\mu_ldx IdI=−μldx 进行积分求解, ∫ I 0 I d I I = − ∫ 0 x ρ μ m d x = > I = I 0 e − μ m x ρ \int_{I_0}^I\frac{dI}{I}=-\int_0^x\rho\mu_mdx=>I=I_0e^{-\mu_mx\rho} ∫I0IIdI=−∫0xρμmdx=>I=I0e−μmxρ,其中 I I 0 \frac{I}{I_0} I0I称为透射系数或透过率。
对于任一元素,质量吸收系数 μ m \mu_m μm是原子序数Z、X射线的波长的函数: μ m ≈ K λ 3 Z 3 \mu_m\approx K\lambda^3Z^3 μm≈Kλ3Z3,K为系数。
对于复杂物质,质量吸收系数 μ m \mu_m μm是个元素的质量吸收系数 μ m i \mu_{mi} μmi及各元素的质量分数 ω i \omega_i ωi的加权平均值: μ m = ∑ ω i μ m i \mu_m=\sum\omega_i\mu_{mi} μm=∑ωiμmi
实验证明,连续X射线穿过物质时的 μ m \mu_m μm相当于一个波长值为有效波长 λ 有效 \lambda_{有效} λ有效所对应的质量吸收系数,有效波长 λ 有效 \lambda_{有效} λ有效和短波限 λ 0 \lambda_{0} λ0关系: λ 有效 = 1.35 λ 0 \lambda_{有效}=1.35\lambda_{0} λ有效=1.35λ0
吸收限:这里的 μ m \mu_m μm和λ应该连续变化,但在实际上 μ m \mu_m μm不是连续变化,在某些波长位置突然增加7-10倍,然后又随着λ的减小而减小。
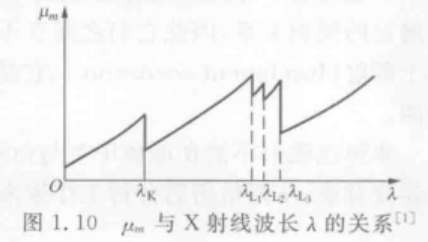
吸收限和光电效应有关。
光电效应(Photoelectric Effect):
当入射X射线光子能量大于吸收体原子某壳层电子的结合能时,光子容易被电子吸收,获得能量的电子从内层逸出称为自由电子(光电子),原子处于相应的激发态。
光电效应消耗大量的入射能量,表现为吸收系数突增,对应的入射波长为吸收限。
荧光辐射(Fluorescent Radiation):
**荧光辐射(二次特征辐射):**由X射线激发产生的特征辐射。属于光致发光的萤光现象。
**荧光辐射的过程:**入射X射线光子能量足够大,把原子内层电子击出产生光电效应,被激出电子的原子处于不稳定激发态,外层电子向内跃迁辐射出一定波长的X射线。
**荧光辐射的应用:**在X射线衍射分析中,荧光辐射是有害的,因为它会增加衍射花样的背底;但在元素分析过程中,它又是X射线荧光光谱分析的基础。
激发荧光辐射的能量条件:欲激发荧光辐射,比如激发K系的荧光辐射,要求入射X射线光子能量必须≥从原子中击出一个K层电子所需做的功: W K = h ν K = h c / λ K W_{K}=h\nu_K=hc/\lambda_K WK=hνK=hc/λK。一旦产生X射线荧光辐射,入射X射线能量杯大量吸收,所以 λ K \lambda_K λK也被称为被照射物质因产生荧光辐射而大量吸收入射X射线的吸收限。
激发荧光辐射的吸收限的影响因素:不同元素,吸收限不同【Z越大,同名(K、L、M)吸收限波长越短,根据 1 λ = K 2 ( Z − σ ) \sqrt{\frac1{\lambda}}=K_2(Z-\sigma) λ1=K2(Z−σ)】
**荧光X射线的能量和波长:**荧光辐射光子的能量一定小于激发它产生的入射X射线的能量,所以荧光辐射光子的波长一定大于入射X射线的波长。
俄歇效应(Auger Effect):
**俄歇效应的过程:**原子内壳层的电子被入射X射线激发形成一个空位,外壳层电子向内壳层空位跃迁并释放出能量,这个能量一方面以光电子的形式释放出来形成荧光辐射;另一方面还可以转移到另一个电子,导致其从原子中激发出来,这个被激发的电子叫俄歇电子,这个过程称为俄歇效应。
**俄歇电子的能量:**原子初始产生空位的壳层能态和跃迁壳层能态以及逸出电子所处壳层的终止能态差。能量是特征的,和入射X射线波长无关,和产生俄歇效应原子种类有关。
**俄歇电子应用:**俄歇电子一般能量很低,只有表面几层原子所产生的俄歇电子才能逃逸出物质表面,所以俄歇电子谱仪是典型的表面成分分析设备。轻元素产生俄歇电子的概率比较大,比重元素强烈,故俄歇效应用于表面轻元素的分析。

(2)X射线吸收效应的应用
①吸收限的应用
1.根据试样化学成分选择阳极靶材
基本原则:入射射线尽可能少地激发样品的荧光辐射。
要求:入射线的波长略长于试样的 λ K \lambda_K λK或者小很多。
X射线管所选靶材原子序数比试样原子序数稍小或者大很多。
Z 靶 ≤ Z 样 + 1 Z_{靶}\leq Z_{样}+1 Z靶≤Z样+1或 Z 靶 > > Z 样 Z_{靶}>> Z_{样} Z靶>>Z样
如果试样中含有多种元素,应根据含量较多的几种元素里原子序数最小的元素来选择。

②滤片选择
X射线产生的K系谱线包括 K α , K β K_{\alpha},K_{\beta} Kα,Kβ谱线,为了获得单一谱线的衍射条纹,需要滤掉另一种谱线。需要找到一种材料,其吸收限 λ K \lambda_K λK正好位于X射线管产生的 K α , K β K_{\alpha},K_{\beta} Kα,Kβ谱线波长之间,尽量贴近 K α K_{\alpha} Kα,即== λ K β ( 光源 ) < λ K ( 滤波片) < λ K α ( 光源 ) \lambda_{K_{\beta}}(光源)<\lambda_K(滤波片)<\lambda_{K_{\alpha}}(光源) λKβ(光源)<λK(滤波片)<λKα(光源)==
把此材料置于光路中,滤片强烈地吸收 K β K_{\beta} Kβ线,对 K α K_{\alpha} Kα吸收很少,即可得到单色的 K α K_{\alpha} Kα辐射。
滤片选择原则为:滤片原子序数比阳极靶材系数小1/2