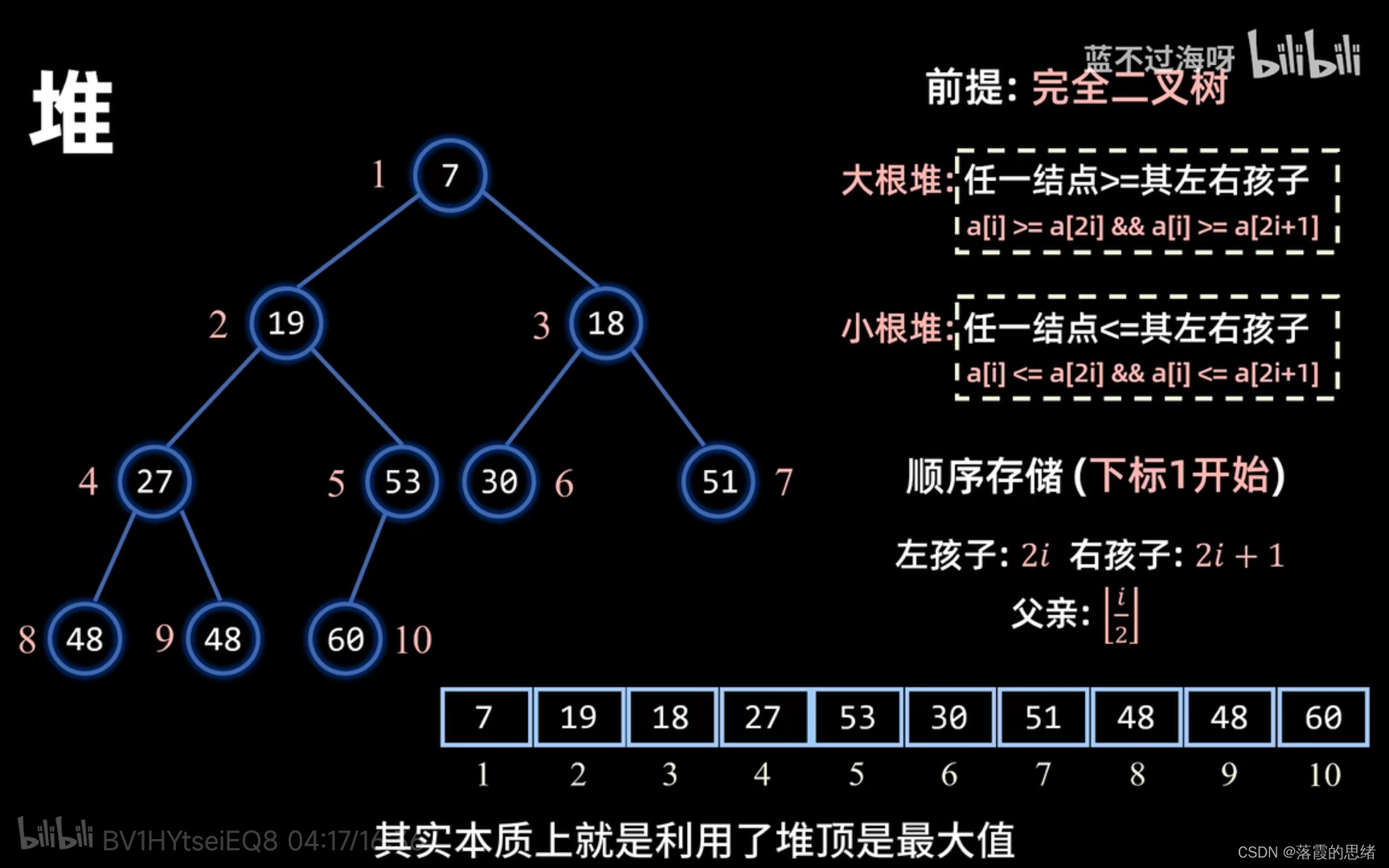
完全二叉树
完全二叉树满足以下两个条件:
-
所有层的节点都完全填满:除了最后一层外,每一层的节点数都是最大节点数,即除了最后一层,其他层的节点数都是满的。
-
最后一层的节点尽可能地向左排列:在满足第一个条件的前提下,最后一层的节点从左到右填充,没有空隙。
完全二叉树的性质包括:
-
高度:完全二叉树的高度通常用 h 表示,对于有 n 个节点的完全二叉树,其高度 h 满足 h=⌊log2n⌋+1。
-
节点数:对于高度为 h 的完全二叉树,其节点总数 n 满足2^(h−1)≤n<2^h。
-
叶子节点:在高度为 h 的完全二叉树中,叶子节点的数量最多为 2^(h−1),最少为 1(当 h = 1 时)。
-
数组表示:完全二叉树可以用数组来表示,其中第 i 个节点(假设根节点为 1)的左子节点为 2i,右子节点为 2i+1,父节点为 ⌊i/2⌋。
-
满二叉树:如果一个完全二叉树的所有层都完全填满,那么它就是一个满二叉树(Full Binary Tree)。
-
二叉堆:完全二叉树常用于实现二叉堆(Binary Heap),二叉堆是一种特殊的完全二叉树,它满足堆的性质,即任意节点的值总是不大于(或不小于)其子节点的值。
二叉堆
二叉堆是一种特殊的二叉树,也是最常见的堆结构,它有两种类型:
-
最大堆(Max Heap):在最大堆中,每个节点的值都 >= 其子节点的值。在最大堆的根节点存储着整个堆中的最大值。
-
最小堆(Min Heap):在最小堆中,每个节点的值都 <= 于其子节点的值。在最小堆的根节点存储着整个堆中的最小值。
堆排序
堆排序(Heap Sort)是一种基于二叉堆数据结构的选择排序算法。它利用堆这种数据结构的特性来对数据进行排序,可以是最大堆或最小堆。
以下是堆排序代码,一开始是建立大根堆,来实现升序排序
堆的建立代码如下
// 堆排序
// 建立堆
public static void BuiltMaxHeap(int arr[], int len){
for(int i = len >> 1; i > 0; i--){ // 从最后一个有孩子节点的节点开始
HeadAdjust(arr, i, len);
}
}
// 调整堆
// num:调整根节点索引值为num的堆;调整的子树的起始位置
// len:整个堆中元素的个数;调整子树的终止位置
public static void HeadAdjust(int arr[], int num, int len){
for (int i = num << 1; i <= len; i *= 2){
if (i + 1 <= len && arr[i + 1] > arr[i]){
i++;
} // 找到孩子节点中最大的节点的索引值i
if (arr[num] < arr[i]) { // 这里是基于交换来实现小元素的下坠
arr[0] = arr[i];
arr[i] = arr[num];
arr[num] = arr[0];
} else {
break;
}
num = i;
}
}如果要基于元素移动并覆盖的方式来调整堆,那么这种调整方法如下
public static void HeadAdjust(int arr[], int num, int len){
arr[0] = arr[num];
for (int i = num << 1; i <= len; i *= 2){
if (i + 1 <= len && arr[i + 1] > arr[i]){
i++;
} // 找到孩子节点中最大的节点的索引值i
if (arr[0] < arr[i]) {
arr[num] = arr[i];
} else {
break;
}
num = i;
}
// 这里是基于移动覆盖元素来实现小元素的下坠
arr[num] = arr[0]; // 移动覆盖元素方法一般都是在循环覆盖完元素后给指定位置赋值
}开始排序
public static void HeapSort(int arr[], int len) {
BuiltMaxHeap(arr, len); // 建立一个堆
for (int i = len; i > 1; i--) { // 之后不断将堆的第一个元素与最后的元素交换位置
arr[0] = arr[1];
arr[1] = arr[i];
arr[i] = arr[0];
HeadAdjust(arr, 1, i - 1); // 交换完位置后调整堆
}
}堆排序时间空间复杂度及稳定性分析
建堆的时间复杂度为:O(n);
排序的时间复杂度:O(n log2 n);
总的时间复杂度:O(n log2 n);
稳定性:不稳定