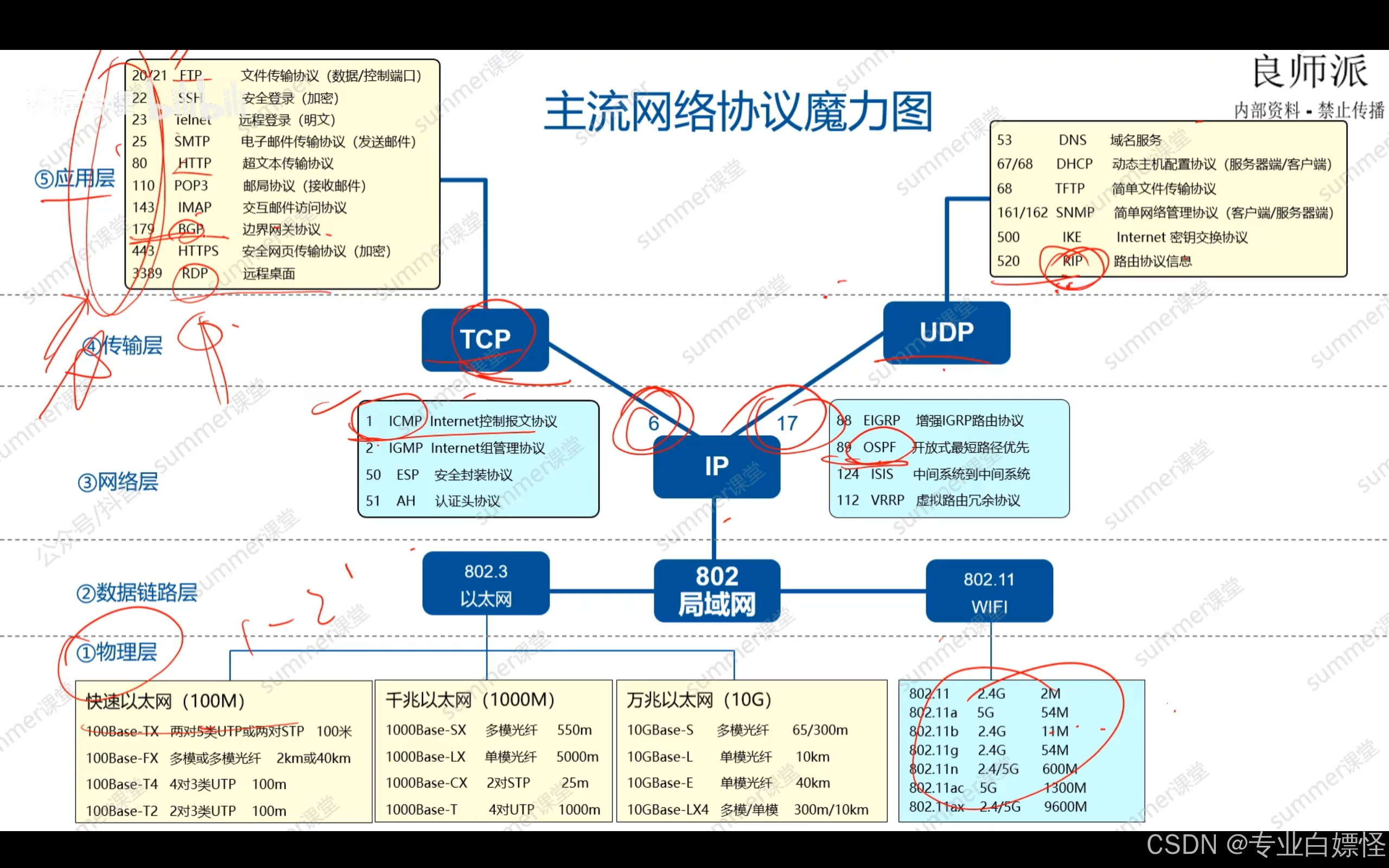
目录
拉格朗日乘子法定理
证明:编辑
应用条件与符号选择
雅可比矩阵
黑塞矩阵
牛顿法
解方程的根的牛顿法
解方程组的根的牛顿法
数值优化的牛顿法(求最值)
拉格朗日乘子法定理

证明:
dSi这一段没看懂……
应用条件与符号选择
符号
f+μigi
max f,则把gi符号调成正的
min f, 则把gi符号调成负的
这样引入的参数都是正的了
感谢——
最优化方法三:等式约束优化、不等式约束优化、拉格朗日乘子法证明、KKT条件_有约束最优化问题 不等式约束-CSDN博客
雅可比矩阵
有多个函数fi,多个变量xi
都是一阶导

黑塞矩阵
都是二阶导
牛顿法
解方程的根的牛顿法
是不动点迭代的特例
每次沿着切线方向下降,与x轴相交
由来:taylor展开
令f(x)=0
x=x_{k+1}即可。
解方程组的根的牛顿法
即解方程组
可以预见
数值优化的牛顿法(求最值)
对f进行泰勒展开
只取省略号前面的
d_k=x-x_k
对d_k求导(即梯度下降)
g_k+Gd_k=0
下降方向
G是黑塞矩阵
理论上这样迭代可以得到最优值(梯度为0)