大家好，这里是效率办公指南！

📅 在处理与时间相关的数据时，DATEDIF函数是Excel中一个非常有用的工具。DATEDIF函数可以计算两个日期之间的差异，无论是天数、月数还是年数。这在处理年龄计算、工龄统计或任何需要日期差的场景中都非常实用。今天，我们将详细介绍DATEDIF函数的使用方法。

DATEDIF函数的语法

DATEDIF(start_date, end_date, "unit")

• start_date：开始日期。

• end_date：结束日期，应大于开始日期。

• unit：计算的单位，可以是以下几种：

  • "Y"：年

  • "M"：月

  • "D"：天

  • "YM"：忽略年份的月数

  • "YD"：忽略年份的天数

  • "MD"：忽略月份的天数

案例一：计算年龄

场景：根据员工的出生日期计算其年龄。

操作：

• 在B2单元格输入公式：

  =DATEDIF(A2, TODAY(), "Y")

  这将返回从出生日期到今天的年数。

案例二：计算工龄

场景：计算员工的工作年限。

操作：

• 在B2单元格输入公式：

  =DATEDIF(A2, TODAY(), "Y")

  这将返回员工的工龄，忽略完整的工作年份后的剩余月数。

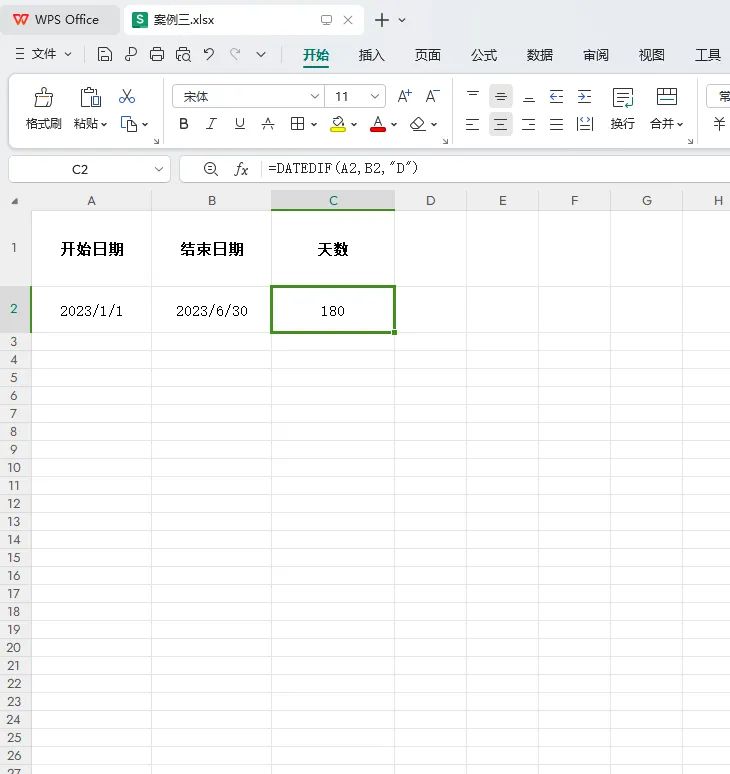
案例三：计算项目持续时间

场景：计算项目从开始到结束的总天数。

操作：

• 在C2单元格输入公式：

  =DATEDIF(A2, B2, "D")

  这将返回项目持续的总天数。

注意事项

• 确保开始日期和结束日期使用正确的日期格式。

• 结束日期必须大于开始日期。

• 根据需要选择合适的单位参数。

总结

DATEDIF函数是一个非常强大的工具，可以帮助我们快速计算日期差异。无论是计算年龄、工龄还是项目持续时间，DATEDIF都能轻松应对。掌握这个函数，将大大提高你在处理日期数据时的效率。如果你有任何疑问或需要进一步的帮助，欢迎在下方留言，我们会尽快为你解答。

微信搜一搜【效率办公指南】，回复【dc56d550b8fd】获取文中案例