开始之前
canvas是一个可以使用脚本在其中绘制图形的 HTML 元素.它本身并不具备绘图能力,需要配合JavaScript使用
用途
- 游戏应用
- 特效字体
- 相册,幻灯片
- 股票行情等动态图像
- 思维图以及图形编辑器等在线可视化工具
基本特性
canvas元素会初始化宽度为300像素和高度为150像素canvas元素通过浏览器渲染后,是透明的,不可见的canvas元素可以使用CSS来定义大小,但在绘制时图像会伸缩以适应它的框架尺寸:如果CSS的尺寸与初始画布的比例不一致,它会出现扭曲。canvas元素原始坐标原点为canvas画布的左上角
基本特性3介绍
见canvas.html代码说明
上述例子中,用css设置的width为450,height为300,对应默认的画布大小300×150,宽高比例分别为1.5和2,
所以我们设置的矩形的宽(100px)高(100px)实现显示的会是
宽:100px×1.5=150px;
高:100px×2=200px;
效果如下图:

绘制线段
- 开启轨迹路径
- 设置线段的起始点
- 设置线段的终点
- 设置线段的样式
- 开始绘制线段
图形绘制
绘制矩形
ctx.fillRect(x,y,width,height) strokeRect(x,y,width,height)
- x: 矩形起点横坐标
- y :矩形起点纵坐标
- width: 矩形长度
- height: 矩形高度
清除矩形区域
ctx.clearRect(x,y,width,height)
- x:清除矩形起点横坐标
- y:清除矩形起点纵坐标
- width:清除矩形长度
- height:清除矩形高度
绘制圆弧
ctx.arc(x, y, radius, starAngle,endAngle, anticlockwise)
- x:圆心的x坐标
- y:圆心的y坐标
- radius: 圆的半径
- straAngle: 开始角度
- endAngle: 结束角度
- anticlockwise: 是否逆时针,(true)为逆时针,(false)为顺时针

渐变
线性渐变
var grans = ctx.createLinearGradient(xStart,yStart,xEnd,yEnd)
- xstart: 渐变开始点x坐标
- ystart: 渐变开始点y坐标
- xEnd: 渐变结束点x坐标
- yEnd: 渐变结束点y坐标
线性渐变颜色 grans.addColorStop(offset,color)
- offset:设定的颜色离渐变结束点的偏移量(0~1)
- color:绘制时要使用的颜色
径向渐变
var cles = ctx.createRadialGradient(xStart,yStart,radiusStart,xEnd,yEnd,radiusEnd)
- xStart: 开始发散圆心x坐标 - yStart: 开始发散圆心y坐标 - radiusStart: 开始发散圆的半径 - xEnd: 结束发散圆心的x坐标 - yEnd: 结束发散圆心的y坐标 - radiusEnd: 结束发散圆的半径
径向渐变颜色rg.addColorStop(offset,color)
- offset:设定的颜色离渐变结束点的偏移量(0~1)
- color:绘制时要使用的颜色
发散偏移量的图

绘制文字
填充文字:context.fillText(text,x,y)
绘制文字轮廓 context.strokeText(text,x,y)
-
text: 要绘制的文字
-
x: 文字起点的x坐标轴
-
y: 文字起点的y坐标轴
ctx.font:设置字体样式 ctx.textAlign:水平对齐方式 start、end、right、center ctx.textBaseline:垂直对齐方式 top、hanging、middle、alphabetic、ideographic、bottom var length=ctx.measureText(text):计算字体宽度(px) length.width:表示字体的宽度
canvas变换:
1. 平移 ctx.translate(x,y)
2. 缩放 ctx.scale(x,y)
3. 旋转 ctx.rotate(angle)
**平移** x: 坐标原点向x轴方向平移x y: 坐标原点向y轴方向平移y **缩放** x: x坐标轴按x比例缩放 y: y坐标轴按y比例缩放 **旋转** angle: 坐标轴旋转x角度(角度变化模型和画圆的模型一样) **两个好用的方法** - ctx.save(): 保存在save()之后所做变换之前的坐标系状态. - ctx.restore():恢复save()保存的坐标系状态 关于这两个方法的使用见 demo.html ## 图形移动 ctx.clearRect(x,y,width,height) 清除画布的操作,用来清除canvas标签上面的所有内容
贝塞尔曲线
- ctx.quadraticCurveTo() 绘制二次贝塞尔曲线,拥有四个参数
参数1,2代表曲线的起点和终点之间点的坐标,参数3,4代表终点坐标 - bezierCurveTo() 绘制三次贝塞尔曲线,拥有六个参数
参数1,2,3,4代表曲线起点和终点之间的两个点坐标,参数5,6代表终点坐标
二阶贝塞尔动画

三阶贝塞尔动画
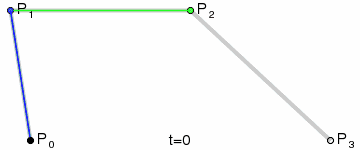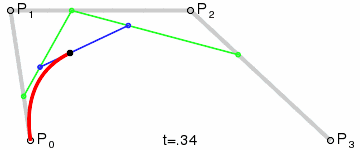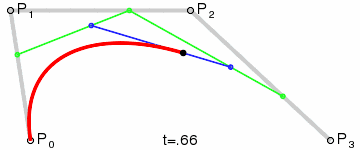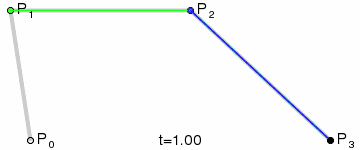
贝塞尔曲线在CSS动画中的有使用,就是在动画的运动过程中,控制速率的变化。
- CSS动画中,使用贝塞尔曲线作为值的属性有两个,transition-timing-function,animation-timing-function,格式为cubic-bezier(P1x,P1y,P2x,P2y),实际应用中的代码实例 transition: all 3.0s cubic-bezier(0.75, 0.25, 0.25, 0.75)。
- 我们大多看到的是,ease,linear,ease-in-out 这样的属性值,其实它们也是贝塞尔曲线值,只不过是官方预定义的,以简化明了的名称,替代了复杂的数值书写方式。
- 以下是一些预定义名称对应的曲线值:
- ease: cubic-bezier(0.25, 0.1, 0.25, 1.0)
- linear: cubic-bezier(0.0, 0.0, 1.0, 1.0)
- ease-in: cubic-bezier(0.42, 0, 1.0, 1.0)
- ease-out: cubic-bezier(0, 0, 0.58, 1.0)
- ease-in-out: cubic-bezier(0.42, 0, 0.58, 1.0)