【leetcode练习·二叉树】用「遍历」思维解题 I

news2024/9/25 6:30:51

本文参考labuladong算法笔记[【强化练习】用「遍历」思维解题 I | labuladong 的算法笔记]

257. 二叉树的所有路径 | 力扣 | LeetCode |

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

示例 1：

输入：root = [1,2,3,null,5]
输出：["1->2->5","1->3"]

示例 2：

输入：root = [1]
输出：["1"]

提示：

  • 树中节点的数目在范围 [1, 100] 内
  • -100 <= Node.val <= 100

前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式，这道题需要用到「遍历」的思维。

你让我求所有根节点到叶子节点的路径，那我遍历一遍二叉树肯定可以搞定，遍历到叶子节点的时候想办法把路径生成出来就行了。

class Solution:
    def binaryTreePaths(self, root: TreeNode) -> List[str]:
        # 遍历一遍二叉树就能出结果了
        self.traverse(root)
        return self.res

    def __init__(self):
        # 记录 traverse 函数递归时的路径
        self.path = []
        # 记录所有从根节点到叶子节点的路径
        self.res = []

    def traverse(self, root: TreeNode):
        if root is None:
            return
        # root 是叶子节点
        if root.left is None and root.right is None:
            self.path.append(str(root.val))
            # 将这条路径装入 res
            self.res.append("->".join(self.path))
            self.path.pop()
            return
        # 前序遍历位置
        self.path.append(str(root.val))
        # 递归遍历左右子树
        self.traverse(root.left)
        self.traverse(root.right)
        # 后序遍历位置
        self.path.pop()

129. 求根节点到叶节点数字之和 | 力扣 | LeetCode |

给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。

每条从根节点到叶节点的路径都代表一个数字：

  • 例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。

计算从根节点到叶节点生成的 所有数字之和 。

叶节点 是指没有子节点的节点。

示例 1：

输入：root = [1,2,3]
输出：25
解释：
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此，数字总和 = 12 + 13 = 25

示例 2：

输入：root = [4,9,0,5,1]
输出：1026
解释：
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此，数字总和 = 495 + 491 + 40 = 1026

提示：

  • 树中节点的数目在范围 [1, 1000] 内
  • 0 <= Node.val <= 9
  • 树的深度不超过 10
class Solution:
    def __init__(self):
        self.path = ""
        self.res = 0

    def sumNumbers(self, root: TreeNode) -> int:
        # 遍历一遍二叉树就能出结果
        self.traverse(root)
        return self.res

    # 二叉树遍历函数
    def traverse(self, root):
        if root is None:
            return
        # 前序遍历位置，记录节点值
        self.path += str(root.val)
        if root.left is None and root.right is None:
            # 到达叶子节点，累加路径和
            self.res += int(self.path)
        # 二叉树递归框架，遍历左右子树
        self.traverse(root.left)
        self.traverse(root.right)

        # 后续遍历位置，撤销节点值
        self.path = self.path[:-1]

199. 二叉树的右视图 | 力扣 | LeetCode |

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1:

输入: [1,2,3,null,5,null,4]
输出: [1,3,4]

示例 2:

输入: [1,null,3]
输出: [1,3]

示例 3:

输入: []
输出: []

提示:

  • 二叉树的节点个数的范围是 [0,100]
  • -100 <= Node.val <= 100

from collections import deque

class Solution:
    # BFS 层序遍历解法
    def rightSideView(self, root) -> list:
        res = []
        if root is None:
            return res
        # BFS 层序遍历，计算右侧视图
        q = deque([root])
        # while 循环控制从上向下一层层遍历
        while q:
            sz = len(q)
            # 每一层头部就是最右侧的元素
            last = q[0]
            for i in range(sz):
                cur = q.popleft()
                # 控制每一层从右向左遍历
                if cur.right:
                    q.append(cur.right)
                if cur.left:
                    q.append(cur.left)
            # 每一层的最后一个节点就是二叉树的右侧视图
            res.append(last.val)
        return res

    # DFS 递归遍历解法
    def rightSideView_DFS(self, root) -> list:
        self.res = []
        # 记录递归的层数
        self.depth = 0
        self.traverse(root)
        return self.res

    # 二叉树遍历函数
    def traverse(self, root):
        if root is None:
            return
        # 前序遍历位置
        self.depth += 1
        if len(self.res) < self.depth:
            # 这一层还没有记录值
            # 说明 root 就是右侧视图的第一个节点
            self.res.append(root.val)
        # 注意，这里反过来，先遍历右子树再遍历左子树
        # 这样首先遍历的一定是右侧节点
        self.traverse(root.right)
        self.traverse(root.left)
        # 后序遍历位置
        self.depth -= 1

298. 二叉树最长连续序列 | 力扣 | LeetCode |

给你一棵指定的二叉树的根节点 root ，请你计算其中 最长连续序列路径 的长度。

最长连续序列路径 是依次递增 1 的路径。该路径，可以是从某个初始节点到树中任意节点，通过「父 - 子」关系连接而产生的任意路径。且必须从父节点到子节点，反过来是不可以的。

示例 1：

输入：root = [1,null,3,2,4,null,null,null,5]
输出：3
解释：当中，最长连续序列是 3-4-5 ，所以返回结果为 3 。

示例 2：

输入：root = [2,null,3,2,null,1]
输出：2
解释：当中，最长连续序列是 2-3 。注意，不是 3-2-1，所以返回 2 。

提示：

  • 树中节点的数目在范围 [1, 3 * 104] 内
  • -3 * 104 <= Node.val <= 3 * 104
class Solution:
    def __init__(self):
        self.maxLen = 0

    def longestConsecutive(self, root: TreeNode) -> int:
        self.traverse(root, 1, float('-inf'))
        return self.maxLen

    # 遍历二叉树，根据父节点的值判断连续的序列长度
    def traverse(self, root: TreeNode, len: int, parentVal: int):
        if root is None:
            return
        if parentVal + 1 == root.val:
            len += 1
        else:
            len = 1
        # 更新最长连续序列的长度
        self.maxLen = max(self.maxLen, len)
        # 遍历框架
        self.traverse(root.left, len, root.val)
        self.traverse(root.right, len, root.val)

988. 从叶结点开始的最小字符串 | 力扣 | LeetCode |

给定一颗根结点为 root 的二叉树，树中的每一个结点都有一个 [0, 25] 范围内的值，分别代表字母 'a' 到 'z'。

返回 按字典序最小 的字符串，该字符串从这棵树的一个叶结点开始，到根结点结束。

注：字符串中任何较短的前缀在 字典序上 都是 较小 的：

  • 例如，在字典序上 "ab" 比 "aba" 要小。叶结点是指没有子结点的结点。 

节点的叶节点是没有子节点的节点。

示例 1：

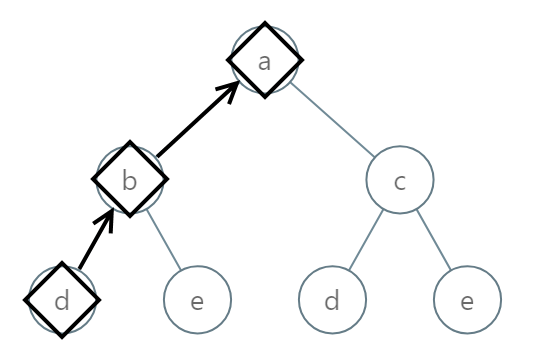
输入：root = [0,1,2,3,4,3,4]
输出："dba"

示例 2：

输入：root = [25,1,3,1,3,0,2]
输出："adz"

示例 3：

输入：root = [2,2,1,null,1,0,null,0]
输出："abc"

提示：

  • 给定树的结点数在 [1, 8500] 范围内
  • 0 <= Node.val <= 25

前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式，这道题需要用到「遍历」的思维。

代码看起来虽然多，但思路非常简单：用 path 维护递归遍历的路径，到达叶子节点的时候判断字典序最小的路径。

不要忘了在叶子节点的时候也要正确维护 path 变量，而且要把 StringBuilder 中的字符串反转才是题目想要的答案。

class Solution:
    def smallestFromLeaf(self, root: TreeNode) -> str:
        self.traverse(root)
        return self.res
    
    # 遍历过程中的路径
    path = ""
    res = None

    # 二叉树遍历函数
    def traverse(self, root):
        if root is None:
            return
        if root.left is None and root.right is None:
            # 找到叶子结点，比较字典序最小的路径
            # 结果字符串是从叶子向根，所以需要反转
            self.path = chr(ord('a') + root.val) + self.path

            s = self.path
            if self.res is None or self.res > s:
                # 如果字典序更小，则更新 res
                self.res = s

            # 恢复，正确维护 path 中的元素
            self.path = self.path[1:]
            return
        # 前序位置
        self.path = chr(ord('a') + root.val) + self.path

        self.traverse(root.left)
        self.traverse(root.right)

        # 后序位置
        self.path = self.path[1:]

1022. 从根到叶的二进制数之和 | 力扣 | LeetCode |

前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式，这道题需要用到「遍历」的思维。

用 path 变量维护每一条从根节点到叶子节点的路径形成的二进制数，到了叶子节点之后将这条路径的二进制数累加到 res 中即可。

class Solution:
    def sumRootToLeaf(self, root: TreeNode) -> int:
        self.path = 0
        self.res = 0
        self.traverse(root)
        return self.res

    def traverse(self, root: TreeNode):
        if root is None:
            return
        if root.left is None and root.right is None:
            # 叶子节点
            self.res += self.path << 1 | root.val
            return
        # 前序位置
        self.path = self.path << 1 | root.val
        self.traverse(root.left)
        self.traverse(root.right)
        # 后序位置
        self.path = self.path >> 1

1457. 二叉树中的伪回文路径 | 力扣 | LeetCode |

前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式，这道题需要用到「遍历」的思维。

遍历一遍二叉树就能得到每条路径上的数字，但这题的考点在于，如何判断一组数字是否存在一个回文串组合？

稍加思考不难想到：如果一组数字中，只有最多一个数字出现的次数为奇数，剩余数字的出现次数均为偶数，那么这组数字可以组成一个回文串。

题目说了 1 <= root.val <= 9，所以我们可以用一个大小为 10 的 count 数组做计数器来记录每条路径上的元素出现次数，到达叶子节点之后根据元素出现的次数判断是否可以构成回文串。

当然，我们也可以用更巧妙的位运算来实现上述逻辑：

1、首先用到异或运算的特性，1 ^ 1 = 0, 0 ^ 0 = 0, 1 ^ 0 = 1。

2、其次用到 n & (n - 1) 去除二进制最后一个 1 的技巧，详见 东哥教你几招常用的位运算技巧。

我同时实现了这两种方法，供你参考。


# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def __init__(self):
        self.count = [0] * 10
        self.res = 0

    def pseudoPalindromicPaths(self, root: TreeNode) -> int:
        self.traverse(root)
        return self.res

    # 二叉树遍历函数
    def traverse(self, root: TreeNode):
        if root is None:
            return
        if root.left is None and root.right is None:
            # 遇到叶子节点，判断路径是否是伪回文串
            self.count[root.val] += 1
            # 如果路径上出现奇数次的数字个数大于 1，
            # 则不可能组成回文串，反之则可以组成回文串
            odd = 0
            for n in self.count:
                if n % 2 == 1:
                    odd += 1
            if odd <= 1:
                self.res += 1
            self.count[root.val] -= 1
            return

        self.count[root.val] += 1
        # 二叉树遍历框架
        self.traverse(root.left)
        self.traverse(root.right)

        self.count[root.val] -= 1

# 用位运算代替数组计数，进一步提升效率
class Solution2:
    def __init__(self):
        self.count = 0
        self.res = 0

    def pseudoPalindromicPaths(self, root: TreeNode) -> int:
        self.traverse(root)
        return self.res

    # 二叉树遍历函数
    def traverse(self, root: TreeNode):
        if root is None:
            return
        if root.left is None and root.right is None:
            # 遇到叶子节点，判断路径是否是伪回文串
            self.count ^= (1 << root.val)
            # 判断二进制中只有一位 1，原理见 https://labuladong.online/algo/frequency-interview/bitwise-operation/
            if (self.count & (self.count - 1)) == 0:
                self.res += 1
            self.count ^= (1 << root.val)
            return
        self.count ^= (1 << root.val)
        # 二叉树遍历框架
        self.traverse(root.left)
        self.traverse(root.right)

        self.count ^= (1 << root.val)

1740. 找到二叉树中的距离 | 力扣 | LeetCode |

给定一棵二叉树的根节点 root 以及两个整数 p 和 q ，返回该二叉树中值为 p 的结点与值为 q 的结点间的 距离 。

两个结点间的 距离 就是从一个结点到另一个结点的路径上边的数目。

示例 1：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 0
输出：3
解释：在 5 和 0 之间有 3 条边：5-3-1-0

示例 2：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 7
输出：2
解释：在 5 和 7 之间有 2 条边：5-2-7

示例 3：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 5
输出：0
解释：一个结点与它本身之间的距离为 0

提示：

  • 树中结点个数的范围在 [1, 104].
  • 0 <= Node.val <= 109
  • 树中所有结点的值都是唯一的.
  • p 和q 是树中结点的值.

这道题很明显是最近公共祖先问题（LCA）的拓展，原版的 LCA 问题是让我们返回最近公共祖先节点，现在相当于是在问 p 和 q 到最近公共祖先的树枝的距离之和。

不过说实话，这题的难度还是比较大的，需要你认真阅读我写的 一文秒杀所有二叉树最近公共祖先问题，理解 LCA 问题解法逐步演进的原理，然后再来看这道题。

具体看代码注释吧，最好结合 二叉树心法（纲领篇） 体悟一下二叉树的遍历顺序，毕竟递归算法不是线性执行的，只要搞明白代码的执行顺序就可以更深刻地理解递归。

class Solution:
    def findDistance(self, root: TreeNode, p: int, q: int) -> int:
        self.lca(root, p, q)
        return self.res

    found = False
    res = 0

    # 定义：当子树中不包含 p 或 q 时，返回 0；
    # 当子树中仅包含 p 或 q 中的一个时，返回 root 到 p 或 q 的距离；
    # 当子树中同时包含 p 和 q 时，返回一个无意义的值（答案会被存在外部变量 res 中）
    def lca(self, root: TreeNode, p: int, q: int) -> int:
        if self.found:
            # found 为 true 时答案已经被记录在全局 res 中
            # 递归函数的返回值已不需要了，此时返回什么值都无所谓
            return 123
        if root is None:
            return 0

        left = self.lca(root.left, p, q)
        right = self.lca(root.right, p, q)

        if left == 0 and right == 0:
            # root 的左右子树都不包含 p 或 q
            if root.val == p or root.val == q:
                return 1
            return 0

        if left != 0 and right != 0 and not self.found:
            # 当前节点 root 就是 p, q 的最近公共祖先节点
            # 答案已经算出来了，更新全局变量
            self.res = left + right
            # 这个递归函数的返回值已经不重要了，让它终止递归
            self.found = True
            return 456

        # 此时 left 和 right 有一个为 0，即只找到了一个节点
        # branch 就是到该节点的距离
        branch = right if left == 0 else left

        if root.val == p or root.val == q:
            self.res = branch

        return branch + 1

1257. 最小公共区域 | 力扣 | LeetCode |

给你一些区域列表 regions ，每个列表的第一个区域都包含这个列表内所有其他区域。

很自然地，如果区域 X 包含区域 Y ，那么区域 X  比区域 Y 大。

给定两个区域 region1 和 region2 ，找到同时包含这两个区域的 最小 区域。

如果区域列表中 r1 包含 r2 和 r3 ，那么数据保证 r2 不会包含 r3 。

数据同样保证最小公共区域一定存在。

示例 1：

输入：
regions = [["Earth","North America","South America"],
["North America","United States","Canada"],
["United States","New York","Boston"],
["Canada","Ontario","Quebec"],
["South America","Brazil"]],
region1 = "Quebec",
region2 = "New York"
输出："North America"

提示：

  • 2 <= regions.length <= 10^4
  • region1 != region2
  • 所有字符串只包含英文字母和空格，且最多只有 20 个字母。

这道题有意思，很显然是一个多叉树最近公共祖先的问题。建议看下这篇文章 二叉树最近公共祖先 中讲到的 1650. 二叉树的最近公共祖先 III。

我们可以用题目输入的 regions 结合哈希表构建多叉树，且节点指向关系是从子节点指向父节点，方便我们根据 region1, region2 回溯最近的公共祖先。构建出来之后可以直接套用 1650 的解题思路，利用 单链表的双指针技巧汇总 中讲的寻找单链表交点的算法找到答案。

# 注意：python 代码由 chatGPT🤖 根据我的 java 代码翻译。
# 本代码的正确性已通过力扣验证，但可能缺失注释。必要时请对照我的 java 代码查看。

class Solution:
    def __init__(self):
        self.tree = {}

    def findSmallestRegion(self, regions: List[List[str]], region1: str, region2: str) -> str:
        # 构建反向链接的多叉树，key 为子节点，value 为父节点
        for list in regions:
            parent = list[0]
            for child in list[1:]:
                self.tree[child] = parent

        # 转化为 1650. 二叉树的最近公共祖先 III 的解法
        return self.lowestCommonAncestor(region1, region2)

    def lowestCommonAncestor(self, p: str, q: str) -> str:
        # 施展链表双指针技巧
        a, b = p, q
        while a != b:
            # a 走一步，如果走到根节点，转到 q 节点
            a = self.tree.get(a, q)
            # b 走一步，如果走到根节点，转到 p 节点
            b = self.tree.get(b, p)
        return a

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2162795.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

spring-boot、spring-cloud、spring-cloud-alibaba的常用依赖的依赖声明及pom文件

spring-boot、spring-cloud、spring-cloud-alibaba的常用依赖的依赖声明及pom文件

copy自若依 父工程pom文件&#xff0c;主要定义了依赖的版本号 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:sch…
阅读更多...
什么是电商云手机？可以用来干什么？

什么是电商云手机？可以用来干什么？

随着电商行业的迅速发展&#xff0c;云手机作为一种创新工具正逐渐进入出海电商领域。专为外贸市场量身定制的出海电商云手机&#xff0c;已经成为许多外贸企业和出海电商卖家的必备。本文将详细介绍电商云手机是什么以及可以用来做什么。 与国内云手机偏向于游戏场景不同&…
阅读更多...
什么是启发式过滤（Heuristic Filtering）？

什么是启发式过滤（Heuristic Filtering）？

定义 启发式过滤是一种技术方法&#xff0c;利用解决问题的技术和算法来识别数据中的模式、趋势或特征。 这种方法通常涉及使用预测分析和近似方法&#xff0c;以便快速做出决策或对信息进行分类。 启发式过滤通常应用于反垃圾邮件软件、防病毒程序和人工智能等领域&#xff0…
阅读更多...
openeuler22.03 LTS 源码编译安装nginx1.22.1

openeuler22.03 LTS 源码编译安装nginx1.22.1

openeuler22.03 LTS 源码编译安装nginx1.22.1 下载安装包 #官网下载nginx1.22.1 wget http://nginx.org/download/nginx-1.22.1.tar.gz安装依赖包 #安装依赖包&#xff0c;NGINX是C语言写的&#xff0c;pcre-devel支持正则表达式&#xff0c;openssl 开启加密 [rootproxy ~]…
阅读更多...
Java面向对象（类和对象）（自己学习整理的资料）

Java面向对象（类和对象）（自己学习整理的资料）

目录 一.面向对象思想 二.类和对象 三&#xff1a;定义类的步骤 四.创建对象 五.用Java代码写一个简单的登录系统 练习 六.关于类的方法 七.类的无参无返回值方法 八.方法的返回值 练习 关于方法调用问题 九.全局变量和局部变量 十.笔记 一.面向对象思想 就只关注参…
阅读更多...
科研绘图系列：R语言分组堆积图（stacked barplot）

科研绘图系列：R语言分组堆积图（stacked barplot）

文章目录 介绍加载R包导入数据数据预处理画图导出数据系统信息介绍 堆积图是一种数据可视化图表，它通过将不同类别的数据以堆叠的形式展现在同一个图表中，来展示各个类别之间的相对大小和它们之间的总和。堆积图可以是柱状图、条形图或面积图的形式，其中每个堆叠的块或区域…
阅读更多...
西门子S7-1200 PLC的配方功能

西门子S7-1200 PLC的配方功能

配方相关指令介绍工控人加入PLC工业自动化精英社群 配方功能主要使用4个指令&#xff0c;READ_DBL和WRIT_DBL用于对配方数据块的读写&#xff0c;RecipeExport和RecipeImport用于配方数据块和CSV文件之间的转化&#xff0c;下面分别介绍这4个指令的使用。 READ_DBL / / / / …
阅读更多...
MMD模型及动作一键完美导入UE5-Blender方案（三）

MMD模型及动作一键完美导入UE5-Blender方案（三）

1、下载并安装blender_mmd_tools插件 1、下载并安装Blender，Blender，下载Blender3.6，下载太新的版本可能会跟blender_mmd_tools不匹配 2、github下载blender_mmd_tools：https://github.com/UuuNyaa/blender_mmd_tools/ 3、Edit->Preference->Add ons->Install F…
阅读更多...
【LinuxC高级】汇总

【LinuxC高级】汇总

ls ls -l&#xff1a;显示文件的详细信息 ls -a&#xff1a;显示隐藏文件 ls -lh&#xff1a;文件大小单位显示 ls -i&#xff1a;显示文件的inode号 修改密码 passwd 用户名 su 用户名 -----> 用户名 su ----> 如果不加用户名&#xff0c;默认切换到超级用户 cd cd 路径…
阅读更多...
Windows 10 on ARM, version 22H2 (updated Aug 2024) ARM64 AArch64 中文版、英文版下载

Windows 10 on ARM, version 22H2 (updated Aug 2024) ARM64 AArch64 中文版、英文版下载

Windows 10 on ARM, version 22H2 (updated Aug 2024) ARM64 AArch64 中文版、英文版下载 基于 ARM 的 Windows 10 请访问原文链接&#xff1a;https://sysin.org/blog/windows-10-arm/&#xff0c;查看最新版。原创作品&#xff0c;转载请保留出处。 作者主页&#xff1a;s…
阅读更多...
MyBatis—Plus 快速上手【后端 22】

MyBatis—Plus 快速上手【后端 22】

MyBatis-Plus 使用入门指南 前言 在Java的持久层框架中&#xff0c;MyBatis因其灵活性和易用性而广受欢迎。然而&#xff0c;随着项目规模的扩大&#xff0c;MyBatis的一些重复性工作&#xff08;如CRUD操作&#xff09;开始显得繁琐。为了解决这一问题&#xff0c;MyBatis-Pl…
阅读更多...
Flink 高可用原理

Flink 高可用原理

Flink 高可用原理 Flink JobManager 高可用 加强了 Flink 集群防止 JobManager 故障的能力。 此特性确保了 Flink 集群将始终持续执行你提交的作业。 JobManager 高可用一般概念是指&#xff0c;在任何时候都有 一个领导者 JobManager&#xff0c;如果领导者出现故障&#xff…
阅读更多...
失踪人口回归（明天开始继续更新学习内容）

失踪人口回归（明天开始继续更新学习内容）

从明天开始继续更新个人学习经验及收获&#xff0c;可能会直接从C入门开始&#xff0c;总结一下C在C的基础上增加的新语法。这篇就当作水贴算了&#xff0c;大家别点赞&#xff0c;留点赞给明天的文章&#xff0c;哈哈 我是安姐的修沟...........
阅读更多...
html TAB、table生成

html TAB、table生成

1. 代码 <!DOCTYPE html> <head> <meta charset"UTF-8"> <title>Dynamic Tabs with Table Data</title> <style> /* 简单的样式 */ .tab-content { display: none; border: 10px solid #ccc; padding: 30px; mar…
阅读更多...
二叉树的基本概念(上)

二叉树的基本概念(上)

文章目录 &#x1f34a;自我介绍&#x1f34a;简介&#x1f34a;树的定义树中的专业术语树的分类 &#x1f34a;二叉树的特性讲解 你的点赞评论就是对博主最大的鼓励 当然喜欢的小伙伴可以&#xff1a;点赞关注评论收藏&#xff08;一键四连&#xff09;哦~ &#x1f34a;自我介…
阅读更多...
【Redis入门到精通六】在Spring Boot中集成Redis（含配置和操作演示）

【Redis入门到精通六】在Spring Boot中集成Redis（含配置和操作演示）

目录 Spring Boot中集成Redis 1.项目创建和环境配置 2.基本操作演示 Spring Boot中集成Redis Spring社区也自定义了一套Redis的客户端&#xff0c;与jedis的操作方式有所差异&#xff0c;Spring中把每个类型的操作都单独封装了起来。下面就让我来带大家了解如何在Spring Boot…
阅读更多...
JavaScript动态数据可视化

JavaScript动态数据可视化

一、引言 在前端开发中&#xff0c;JavaScript无疑是最核心的技术之一。它能够处理各种交互逻辑&#xff0c;实现复杂的功能。本文将通过一个动态数据可视化的案例&#xff0c;展示如何使用JavaScript实现复杂功能。动态数据可视化能够将大量数据以直观、生动的方式呈现&#…
阅读更多...
从 Tesla 的 TTPoE 看资源和算法

从 Tesla 的 TTPoE 看资源和算法

特斯拉的 ttpoe 出来有一段时间了&#xff0c;不出所料网上一如既往的一堆 pr 文&#xff0c;大多转译自 演讲 ppt 和 Replacing TCP for Low Latency Applications&#xff0c;看了不下 20 篇中文介绍&#xff0c;基本都是上面这篇文章里的内容&#xff0c;车轱辘话颠来倒去。…
阅读更多...
Python网络爬虫获取Wallhaven壁纸图片(源码)

Python网络爬虫获取Wallhaven壁纸图片(源码)

** 话不多说&#xff0c;直接附源码&#xff0c;可运行&#xff01; ** import requests from lxml import etree from fake_useragent import UserAgent import timeclass wallhaven(object):def __init__(self):# yellow# self.url "https://wallhaven.cc/search?co…
阅读更多...
前端vue-作用域插槽的传值，子传父，父用obj对象接收

前端vue-作用域插槽的传值，子传父，父用obj对象接收

阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023