前面20个选择题吧

编程题

T1、爆破

时间限制：3000MS

内存限制：589824KB

题目描述：

小明当起了矿场的爆破工程师。小明工作的矿场可以看作一个N x N的二维网格，小明可以将一个炸弹放置到矿场的任意位置，若干时间后炸弹会爆炸，将炸弹所在处及相邻位置炸开，让工人们可以轻松获得那些位置的矿物。现在给出这个矿场的矿物数量分布，请你帮小明找出一个最佳位置，使得炸完后能获得的矿物数量最大。你只需要告诉小明这个最大数量即可。

在第 i 行 j 列的矿物数量为a[ i ][ j ](当1 ≤ i，j ≤ N)，否则为0(即超出矿场边界时不会获得任何矿物)。若放置炸弹在(i，j)，爆炸范围为(i，j)，(i + 1，j)，(i，j + 1)，(i - 1，j)，(i，j - 1)。注意小明只能把炸弹放置到矿场内，但可能爆炸范围超出边界。

输入描述

第一行一个整数N，表示小明工作的矿场大小。
接下来N行，每行N个整数。接下来的第 i 行形如a[ i ][1]a[ i ][2]…a[ i ][N]。表示这矿场内所有位置的矿物数量。
对于100%的数据，1≤N≤800,0≤a[ i ][ j ]≤100000

输出描述

输出一个整数表示小明安放一个炸弹，其爆炸范围内矿物数量之和的最大值

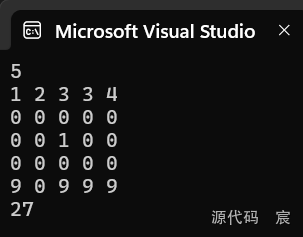
样例输入

5
1 2 3 3 4
0 0 0 0 0
0 0 1 0 0
0 0 0 0 0
9 0 9 9 9

样例输出

27

提示
小明安放炸弹在第5行第4列，能获得最大的矿物数量之和。

C++实现代码

#include <bits/stdc++.h>
#include <iostream>

using namespace std;

int main() {
	int N;
	cin >> N;
	vector<vector<int>> v(N, vector<int>(N, 0));
	for (int i = 0; i < N; i++) {
		for (int j = 0; j < N; j++) {
			cin >> v[i][j];
		}
	}

	int ans = 0;
	vector<vector<int>> directs = { {0, 0}, {1, 0}, {-1, 0}, {0, -1}, {0, 1} };
	for (int i = 0; i < N; i++) {
		for (int j = 0; j < N; j++) {
			int cur = 0;
			for (int k = 0; k < 5; k++) {
				int dx = i + directs[k][0];
				int dy = j + directs[k][1];
				if (dx >= 0 && dx < N && dy >= 0 && dy < N) {
					cur += v[dx][dy];
				}
			}
			ans = max(ans, cur);
		}
	}
	cout << ans << endl;
	return 0;
}

T2、生产

时间限制:3000MS

内存限制:589824KB

题目描述:

小明正在帮一个工厂规划生产计划。小明已经知道未来 n 天工厂会有的情况，初始时机器热量为0，如果第 i 天启动生产，那么热量会增加a_i，产生b_i的收益。若第 i 天没有生产，则热量会减少c_i。小明知道他应该保证在任何情况下热量都不大于阈值T，否则机器会损坏。小明想知道在最佳规划下，工厂最大能获得多少收益。注意热量最低为0，再降温将无效

输入描述

第一行两个整数n和T，表示工厂规划天数和热量阈值
第二行3n个整数a₁b₁c₁a₂b₂c₂…a_nb_nc_n，含义如题面。
对于100%的数据，
1≤n≤3000，1≤T≤100，0≤a_i，c_i≤T，0≤b_i≤100000

输出描述

输出一个整数表示答案。

样例输入

3 3
2 5 1 2 6 1 2 2 3

样例输出

7

提示
第一天生产，热量从0变成2，收益5。
第二天休息，热量从2变成1，收益0。
第三天生产，热量从1产成3，刚好在阈值范围内，收益2。

C++实现代码

#include <bits/stdc++.h>
#include <iostream>

using namespace std;

int main() {
	int n, T;
	cin >> n >> T;
	vector<int> a(n), b(n), c(n);
	for (int i = 0; i < n; i++) {
		cin >> a[i] >> b[i] >> c[i];
	}
	vector<int> dp(T + 1, -3000);
	dp[0] = 0;
	for (int i = 0; i < n; i++) {
		vector<int> tmp(T + 1, -3000);
		for (int j = 0; j <= T; j++) {
			// 选择生产
			if (j + a[i] <= T) {
				tmp[j + a[i]] = max(tmp[j + a[i]], dp[j] + b[i]);
			}
			// 不生产
			tmp[max(0, j - c[i])] = max(tmp[max(0, j - c[i])], dp[j]);
		}
		dp = tmp;
	}
	cout << *max_element(dp.begin(), dp.end()) << endl;
	return 0;
}

之后我会持续更新，如果喜欢我的文章，请记得一键三连哦，点赞关注收藏，你的每一个赞每一份关注每一次收藏都将是我前进路上的无限动力 ！！！↖(▔▽▔)↗感谢支持！