目录
一、矩阵SGEMM
二、SGEMM的各种实现
1、cpu版本的实现
2、GPU并行计算最初始的版本
GPU中数据的移动
4、LDS.128 float4* 优化
5、__syncthreads()位置优化
6、blank conflict优化
bank概念
bank conflict
bank conflict危害和处理后的收益
读数据bank conflict的优化
7、流水并行化——Double Buffering
8、cublas
很久没有学习cuda编程相关的知识了,在《CUDA编程一、基本概念和cuda向量加法》博客中立了flag要把矩阵计算以及attention相关的基本算子实现一遍,最终能采用C++和cuda来实现transformer的前向推理。去年把cuda中的SGEMM学习了一下,没有形成学习记录,写成博客,在完成第二篇博客后,已经鸽了快一年了。最近工作不是特别忙,把之前学习的SGEMM收获的知识写成博客。
一、矩阵SGEMM
SGEMM顾名思义就是通用的单精度矩阵乘法,单精度就是float32(还有双精度以及半精度等)。其数学定义如下:
是
的矩阵,
是
维矩阵,
是
维矩阵,按照矩阵乘法的定义有
其中 ,也就是C中的每个元素是A中一行和B中的一列计算内积得到的结果,它的计算量或者计算次数是M*N*K次乘法和M*N*(K-1)次加法,由于K一般比较大,因此在说一个矩阵计算量的时候一般是2*M*N*K。
为了衡量一个矩阵乘法的效率,可以采用FLOPS(Float Point Operations Per Second)——每秒的浮点运算次数,FLOPS=Float Point Operations/Time。
二、SGEMM的各种实现
1、cpu版本的实现
cpu版本的实现简单直白,直接采用3层for循环就可以解决,A[768,768]、B[768,1024],A中的每个数是1.0,B中的是2.0。完整代码如下(注意实现的过程中把矩阵都转化为一维的列表):
#include<iostream>
#include<sys/time.h>
void matrix_init(float num, float *m, int row, int col);
int main(){
struct timeval start;
struct timeval end;
int row = 768;
int K = 768;
int col = 1024;
// 分配内存
float *A = new float[row * K];
float *B = new float[K * col];
float *C = new float[row * col];
// 初始化
matrix_init(1.0, A, row, K);
matrix_init(2.0, B, K, col);
matrix_init(0.0, C, row, col);
// 记录耗时
gettimeofday(&start,NULL);
// 矩阵计算
for (int count = 0;count <10; count++){
for(int i=0; i < row; i++){
for (int j=0; j < col; j++){
float sum = 0.0;
for(int n=0; n<K; n++){
sum += A[i * K + n] * B[n * col + j];
}
C[i*col + j] = sum;
}
}
}
gettimeofday(&end,NULL);
float time_use;
time_use = (end.tv_sec-start.tv_sec)*1000000+(end.tv_usec-start.tv_usec);//微秒
// 输出耗时信息,以及矩阵C的元素结果值对不对
std::cout<<"cpu mat mul each time is :"<<time_use/1000/10<<" ms \n";
std::cout<<"C[0] == "<<C[0]<<std::endl;
std::cout<<"C[-1] == "<<C[row*col-1]<<std::endl;
delete[]A;
delete[]B;
delete[]C;
return 0;
}
void matrix_init(float num, float *m, int row, int col){
for(int i=0; i < row; i++){
for ( int j = 0; j < col; j++){
m[ i * col + j] = num;
}
}
}运行结果:


结果矩阵C中的结果是2*768=1536,结果和理论一致;耗时2秒,效率的话不用看了,很低。
2、GPU并行计算最初始的版本
对于一个矩阵乘法运算,采用GPU运行,一个比较直观的想法就是结果矩阵C中有多少个元素,我们就开启多少个线程来计算,并且为了更好的效率,我们把每个block的线程都用尽。对于矩阵A[M,K],B[K,N]乘法得到C[M,N],因此可以这样设计griddim和blockdim:
const int BM = 32, BN = 32;
dim3 blockDim(BN, BM);
dim3 gridDim((N + BN - 1) / BN, (M + BM - 1) / BM);核函数如下
__global__ void matrixMulV0(float *C, float *A, float *B, int row, int col, int K){
int tx = threadIdx.x + blockIdx.x * blockDim.x; //第二个矩阵的列方向
int ty = threadIdx.y + blockIdx.y * blockDim.y; // 第一个矩阵的行方向;
if (ty<row && tx< col){
float c = 0.0;
for(int i=0; i<K;i++){
c += A[ty*K+i] * B[i*col + tx];
}
C[ty*col + tx] = c;
}
}总的线程数目就是M*N个(这里只考虑矩阵的维度是特殊的可以把BM和BN除尽,如果不能除尽则需要考虑加padding或者在核函数中使用条件逻辑控制,这个时候总的线程数目仍然就是M*N,采用条件逻辑的时候,有部分线程是空闲的,并不会执行计算逻辑)。
同样令M=768,K=768,N=1024,A的矩阵元素为1.0,B的矩阵元素为2.0,采用如下代码执行上述cuda核。测试环境是4090显卡,cuda版本如下
nvcc: NVIDIA (R) Cuda compiler driver
Copyright (c) 2005-2023 NVIDIA Corporation
Built on Mon_Apr__3_17:16:06_PDT_2023
Cuda compilation tools, release 12.1, V12.1.105
Build cuda_12.1.r12.1/compiler.32688072_0
测试代码来自nicolaswilde / cuda-sgemm中的测试代码:
#include<iostream>
#include<sys/time.h>
#include<stdio.h>
#include<float.h>
#include <tuple>
__global__ void matrixMulV0(float *C, float *A, float *B, int row, int col, int K){
int tx = threadIdx.x + blockIdx.x * blockDim.x; //第二个矩阵的列方向
int ty = threadIdx.y + blockIdx.y * blockDim.y; // 第一个矩阵的行方向;
if (ty<row && tx< col){
float c = 0.0;
for(int i=0; i<K;i++){
c += A[ty*K+i] * B[i*col + tx];
}
C[ty*col + tx] = c;
}
}
void matrix_init(float num, float *m, int row, int col);
std::tuple<float, float, float> testPerformance(void (*gpuSgemm) (float *, float *, float *, const int, const int, const int), dim3 gridDim, dim3 blockDim, const int M, const int N, const int K, const int repeat, int gpu_id);
int main(){
const int M_list[1] = {768};
const int N_list[1] = {768};
const int K_list[1] = {1024};
const int outer_repeat = 10, inner_repeat=10;
const int gpu_id = 3;
const int TESTNUM = 1;
{
const int BM = 32, BN = 32;
void (*gpuSgemm) (float *, float *, float *, const int, const int, const int) = matrixMulV0;
printf("\n Kernal naive matrixMulV0 \n");
{
for(int i=0; i< TESTNUM; i++){
const int M = M_list[i], N = N_list[i], K = K_list[i];
dim3 blockDim(BN, BM);
dim3 gridDim((N + BN - 1) / BN, (M + BM - 1) / BM);
float total_sec = 0.0;
float max_sec = 0.0;
float min_sec = FLT_MAX;
std::tuple<float, float, float> result;
for (int j=0;j< outer_repeat; j++){
result = testPerformance(gpuSgemm, gridDim, blockDim, M, N, K, inner_repeat, gpu_id);
float this_sec = std::get<0>(result);
max_sec = max(max_sec, this_sec);
min_sec = min(min_sec, this_sec);
total_sec += this_sec;
}
float c_0 = std::get<1>(result);
float c_l = std::get<2>(result);
float avg_sec = total_sec / outer_repeat;
float avg_Gflops = ((double)M) * N * K * 2 / 1024 / 1024 / 1024 / avg_sec;
printf("M N K =%6d %6d %6d, Time =min_time:%11.5lf ms avg_time:%11.5lf ms max_time:%11.5lf ms, AVG Performance:%11.5lf Gflops C[0]:%12.5f c[-1]:%12.5f \n", M, N, K, min_sec*1000, avg_sec*1000, max_sec*1000, avg_Gflops, c_0, c_l);
}
}
}
return 0;
}
void matrix_init(float num, float *m, int row, int col){
for(int i=0; i < row; i++){
for ( int j = 0; j < col; j++){
m[ i * col + j] = num;
}
}
}
std::tuple<float, float, float> testPerformance(void (*gpuSgemm) (float *, float *, float *, const int, const int, const int), dim3 gridDim, dim3 blockDim, const int M, const int N, const int K, const int repeat, int gpu_id){
cudaSetDevice(gpu_id);
size_t size_a = M * K * sizeof(float);
size_t size_b = K * N * sizeof(float);
size_t size_c = M * N * sizeof(float);
float *d_a, *d_b, *d_c;
cudaMallocManaged(&d_a, size_a);
cudaMallocManaged(&d_b, size_b);
cudaMallocManaged(&d_c, size_c);
matrix_init(1.0, d_a, M, K);
matrix_init(2.0, d_b, K, N);
matrix_init(0.0, d_c, M, N);
cudaEvent_t start, end;
cudaEventCreate(&start);
cudaEventCreate(&end);
cudaEventRecord(start);
for (int i = 0; i < repeat; i++)
gpuSgemm<<<gridDim, blockDim>>>(d_c, d_a, d_b, M, N, K);
cudaEventRecord(end);
cudaEventSynchronize(end);
float msec, sec;
cudaEventElapsedTime(&msec, start, end);
sec = msec / 1000.0 / repeat;
float c_0 = d_c[0];
float c_l = d_c[M*N-1];
cudaFree(d_a);
cudaFree(d_b);
cudaFree(d_c);
return std::make_tuple(sec, c_0, c_l);
}
得到如下结果
M N K = 768 768 1024, Time =min_time: 0.62680 ms avg_time: 0.81891 ms max_time: 2.48285 ms, AVG Performance: 1373.77502 Gflops C[0]: 2048.00000 c[-1]: 2048.00000平均时间为0.8ms,相对CPU版本提速2500倍。它的计算效率为1373.77502 Gflops约为1.4T,这个数值肯定不行,远远低于4090显卡的性能,官方宣称是80Tflops,这个几乎才1.75%的性能,有很大的优化空间。继续把矩阵的维度调整一下,A和B矩阵的值也调整
const int M_list[15] = {128, 192, 256, 384, 512, 768, 1024, 1536, 2048, 3072, 4096, 6144, 8192, 12288, 16384};
const int N_list[15] = {128, 192, 256, 384, 512, 768, 1024, 1536, 2048, 3072, 4096, 6144, 8192, 12288, 16384};
const int K_list[15] = {128, 192, 256, 384, 512, 768, 1024, 1536, 2048, 3072, 4096, 6144, 8192, 12288, 16384};
matrix_init(1.23456789, d_a, M, K);
matrix_init(2.23456789, d_b, K, N);后续的测试还是同样以这个输入进行测试,性能结果如下:
M N K = 128 128 128, Time =min_time: 0.04229 ms avg_time: 0.22072 ms max_time: 1.81187 ms, AVG Performance: 17.69753 Gflops C[0]: 353.11710 c[-1]: 353.11710
M N K = 192 192 192, Time =min_time: 0.04895 ms avg_time: 0.04997 ms max_time: 0.05130 ms, AVG Performance: 263.82382 Gflops C[0]: 529.67566 c[-1]: 529.67566
M N K = 256 256 256, Time =min_time: 0.06656 ms avg_time: 0.06787 ms max_time: 0.07055 ms, AVG Performance: 460.44287 Gflops C[0]: 706.23425 c[-1]: 706.23425
M N K = 384 384 384, Time =min_time: 0.11816 ms avg_time: 0.12222 ms max_time: 0.12933 ms, AVG Performance: 862.93158 Gflops C[0]: 1059.35071 c[-1]: 1059.35071
M N K = 512 512 512, Time =min_time: 0.19968 ms avg_time: 0.20504 ms max_time: 0.21402 ms, AVG Performance: 1219.30286 Gflops C[0]: 1412.46008 c[-1]: 1412.46008
M N K = 768 768 768, Time =min_time: 0.48876 ms avg_time: 0.49678 ms max_time: 0.50391 ms, AVG Performance: 1698.42651 Gflops C[0]: 2118.68188 c[-1]: 2118.68188
M N K = 1024 1024 1024, Time =min_time: 0.97925 ms avg_time: 0.99610 ms max_time: 1.02298 ms, AVG Performance: 2007.83984 Gflops C[0]: 2824.93188 c[-1]: 2824.93188
M N K = 1536 1536 1536, Time =min_time: 2.44675 ms avg_time: 2.48080 ms max_time: 2.52948 ms, AVG Performance: 2720.89233 Gflops C[0]: 4237.43164 c[-1]: 4237.43164
M N K = 2048 2048 2048, Time =min_time: 5.09768 ms avg_time: 5.34682 ms max_time: 5.66057 ms, AVG Performance: 2992.43506 Gflops C[0]: 5649.93164 c[-1]: 5649.93164
M N K = 3072 3072 3072, Time =min_time: 13.11580 ms avg_time: 13.29336 ms max_time: 13.38286 ms, AVG Performance: 4062.17798 Gflops C[0]: 8474.93164 c[-1]: 8474.93164
M N K = 4096 4096 4096, Time =min_time: 30.10703 ms avg_time: 30.36362 ms max_time: 30.72512 ms, AVG Performance: 4215.57031 Gflops C[0]: 11299.93164 c[-1]: 11299.93164
M N K = 6144 6144 6144, Time =min_time: 113.35250 ms avg_time: 113.74327 ms max_time: 113.98656 ms, AVG Performance: 3798.02686 Gflops C[0]: 16949.73047 c[-1]: 16949.73047
M N K = 8192 8192 8192, Time =min_time: 268.40472 ms avg_time: 270.00385 ms max_time: 271.15201 ms, AVG Performance: 3792.53833 Gflops C[0]: 22597.73047 c[-1]: 22597.73047
M N K = 12288 12288 12288, Time =min_time: 868.66339 ms avg_time: 870.03516 ms max_time: 871.91431 ms, AVG Performance: 3972.25317 Gflops C[0]: 33893.73047 c[-1]: 33893.73047
M N K = 16384 16384 16384, Time =min_time: 2016.83740 ms avg_time: 2018.53320 ms max_time: 2020.41675 ms, AVG Performance: 4058.39233 Gflops C[0]: 45189.73047 c[-1]: 45189.73047最大的浮点计算数是4058GFLOPS,相对官方标称也才5%的性能。为啥差这么多呢,下文慢慢分析和优化。
GPU中数据的移动
有一个大的概念:GPU上进行矩阵计算,首先要把数据从CPU拷贝到GPU的全局内存中,也就常说的显存。运算的过程中线程束中的线程把数据从GPU的全局内存中把矩阵中的值按需获取后转移到GPU中的寄存器(register)中,采用cuda Core中的相关的指令或者tensor Core来实现计算,并把结果存储在寄存器中,然后再写回GPU的全局内存中,最后把结果从GPU全局内存转移到CPU中。如图,显示数据从CPU内存到GPU内存的示意图:

并且速度上 global memory、shared memory 、register 是逐级递减的,并且global memory、shared memory的数据传输速度相差几个数量级,网上有些资料表明, global memory的访问需要数百(500)个时钟周期,shared memory 的访问数十(1-20)个时钟周期,而register 一般默认为是1个时钟周期。
对于上述矩阵乘法计算次数是固定不变的,那么在相同的硬件下,加速数据从CPU到GPU的全局内存,以及全局内存最终到register这个传输过程,才能减少整个矩阵乘法的时间。
先看看上述乘法算子中,计算C矩阵中每个元素的具体情形。如下图

矩阵C中的每一个元素(红色方块)的计算需要:从A矩阵中读取一行(浅咖啡色矩形)K个元素,也需要从B矩阵中读取一列(浅蓝色矩形)K个元素,因此计算一个C中的元素,需要从global memory加载2K次,完全计算C矩阵就需要从global memory中加载数据2MNK次;这样就导致一个重复读取的问题,对于C中的同一行的N个元素,需要重复的读取A中的一行K个元素N次;对于C中的同一列M个元素需要重复的读取B中一列K个元素M次;这样的重复读取肯定是影响效率的。有没有好的办法减小从global memory重复读取的次数呢?利用矩阵分块+Shared Memory可以缓解上述大量重复读取的问题。
3、矩阵分块+Shared Memory优化
具体思路就是:把结果矩阵C划分为一系列的一级矩阵块,大小为,GPU的一个block负责完成计算;block中的每个线程计算一级矩阵块中的一个二级矩阵块大小为
;在进行计算之前,每个线程从global memory读取A和B矩阵一定的数据到划定的Shared Memory中,后续的计算(是指每个线程计算
大小的二级矩阵的部分结果)每个线程直接从Shared Memory中获取数据,而不是从global memory中获取数据,这样就可以减少上述数据加载大量重复的次数。由于Shared Memory的大小有限,因此从A和B加载数据到Shared Memory上的时候,每次加载
大小的数据到Shared Memory A上,
大小的数据到Shared Memory B上。A 矩阵按行滑动,B矩阵按列滑动,示意图如下:

对比数据从global memory的加载次数
初始版本:总体上需要,C的每个元素需要
次
矩阵分块+Shared Memory版本:总体上需要,C的每个元素需要
次
当和
越大,那么从global memory的加载次数就越小,由于GPU的Shared Memory的大小有限制,因此不能无限的增大
和
。同时GPU的架构特性决定一个block中的register也是有限的,一个block中的线程数量不能超过1024;计算过程中每个线程需要一定数量的register来存储C矩阵的中间结果(也就是TM*TN的二级矩阵),计算过程中数据读取global memory到Shared Memory也是需要一定的register。这些总体因素都会限制BM、BN、BK、TM和TN具体的设置,先考虑一组比较优秀的参数,《深入浅出GPU优化系列:GEMM优化(二)》给出了实验最佳结果显示:
核函数代码如下:
__global__ void matrixMulShareMemoryV1(float * __restrict__ C, float * __restrict__ A, float * __restrict__ B, int row, int col, int K){
// block_size=128,BK=8 BM=BN=128, TM=TN=8
// 矩阵C分成[block_size][block_size]维度的小块,一个Block负责计算,设置16*16=256个线程,每个线程计算subC中的8*8的子矩阵元素点;
// A和B矩阵每次加载进sharedMemo维度是[block_size][BK]=128*8,因此每个线程每次迭代的时候load A 和 B的4个元素到sharedMemo中。
// 每个线程都要加载自己的部分,加载完以后,每个线程都可以使用所有线程加载进sharedMemo的数据,执行8*8的子矩阵的计算
const int BM = 128;
const int BN = 128;
const int BK = 8;
const int TM = 8;
const int TN = 8;
__shared__ float s_a[BM][BK];
__shared__ float s_b[BK][BN];
float sub_c[TM][TN] = {0.0};
const int bx = blockIdx.x;
const int by = blockIdx.y;
const int tx = threadIdx.x;
const int ty = threadIdx.y;
//一个block中的线程的序号
const int tid = blockDim.x * ty + tx;
// shared memory中A的行和列关系
int load_a_sh_m = tid/2;
//被2整除的就是0 不能整除的就是4
int load_a_sh_k = (tid%2)*4;
// shared memory中B的行和列关系
int load_b_sh_k = tid/32;
int load_b_sh_n = (tid%32)*4;
// global A的所在行
int load_a_gl_m = by*BM + load_a_sh_m;
// global B的所在列
int load_b_gl_n = bx*BN + load_b_sh_n;
for (int bk=0; bk<(K+BK-1)/BK;bk++){
//A在global memory的所在列
int load_a_gl_k = load_a_sh_k + bk*BK;
int a_gl_adress = load_a_gl_m * K + load_a_gl_k;
//把A中的以a_gl_adress为起点的4个元素复制到s_a中以[load_a_sh_m]*[load_a_sh_k]为起点的4个地址上
for (int i=0;i<4;i++){
s_a[load_a_sh_m][load_a_sh_k+i] = A[a_gl_adress+i];
}
//B在global memory的所在行
int load_b_gl_k = load_b_sh_k + bk * BK;
int b_gl_adress = load_b_gl_k * K + load_b_gl_n;
for (int i=0;i<4;i++){
s_b[load_b_sh_k][load_b_sh_n+i] = B[b_gl_adress+i];
}
// 以上实现所有线程把自己负责的4个数据加载到sharedMemory中
__syncthreads();
#pragma unroll
for(int j=0; j<BK; j++){
#pragma unroll
for(int m=0; m<TM; m++){
#pragma unroll
for(int n=0; n<TN; n++){
// sharedMemory s_a的行 针对不同的线程
int index_a_sh_m = ty*TM + m;
// sharedMemory s_b的列 针对不同的线程
int index_b_sh_n = tx*TN + n;
sub_c[m][n] += s_a[index_a_sh_m][j] * s_b[j][index_b_sh_n];
}
}
}
__syncthreads();
}
#pragma unroll
for(int m=0;m<TM;m++){
int c_gl_m = by*BM + ty*TM + m;
#pragma unroll
for (int n=0; n<TN;n+=4){
int c_gl_n = bx*BN + tx*TN + n;
int c_gl_adress = c_gl_m * col + c_gl_n;
for (int i=0; i<4;i++){
C[c_gl_adress+i] = sub_c[m][n+i];
}
}
}
}结果如下:
M N K = 128 128 128, Time =min_time: 0.04741 ms avg_time: 0.72400 ms max_time: 6.80796 ms, AVG Performance: 5.39539 Gflops C[0]: 353.11710 c[-1]: 353.11710
M N K = 192 192 192, Time =min_time: 0.06154 ms avg_time: 0.06413 ms max_time: 0.06943 ms, AVG Performance: 205.56502 Gflops C[0]: 529.67566 c[-1]: 529.67566
M N K = 256 256 256, Time =min_time: 0.08509 ms avg_time: 0.08693 ms max_time: 0.08929 ms, AVG Performance: 359.50082 Gflops C[0]: 706.23425 c[-1]: 706.23425
M N K = 384 384 384, Time =min_time: 0.11336 ms avg_time: 0.11772 ms max_time: 0.13036 ms, AVG Performance: 895.91907 Gflops C[0]: 1059.35071 c[-1]: 1059.35071
M N K = 512 512 512, Time =min_time: 0.16445 ms avg_time: 0.18931 ms max_time: 0.20511 ms, AVG Performance: 1320.60706 Gflops C[0]: 1412.46008 c[-1]: 1412.46008
M N K = 768 768 768, Time =min_time: 0.40643 ms avg_time: 0.41232 ms max_time: 0.41871 ms, AVG Performance: 2046.32849 Gflops C[0]: 2118.68188 c[-1]: 2118.68188
M N K = 1024 1024 1024, Time =min_time: 0.62863 ms avg_time: 0.65641 ms max_time: 0.68567 ms, AVG Performance: 3046.89893 Gflops C[0]: 2824.93188 c[-1]: 2824.93188
M N K = 1536 1536 1536, Time =min_time: 1.50856 ms avg_time: 1.53321 ms max_time: 1.55945 ms, AVG Performance: 4402.51465 Gflops C[0]: 4237.43164 c[-1]: 4237.43164
M N K = 2048 2048 2048, Time =min_time: 2.28475 ms avg_time: 2.34459 ms max_time: 2.49518 ms, AVG Performance: 6824.21631 Gflops C[0]: 5649.93164 c[-1]: 5649.93164
M N K = 3072 3072 3072, Time =min_time: 4.67353 ms avg_time: 4.81607 ms max_time: 4.91315 ms, AVG Performance:11212.47168 Gflops C[0]: 8474.93164 c[-1]: 8474.93164
M N K = 4096 4096 4096, Time =min_time: 7.57002 ms avg_time: 8.20463 ms max_time: 8.76011 ms, AVG Performance:15600.95508 Gflops C[0]: 11299.93164 c[-1]: 11299.93164
M N K = 6144 6144 6144, Time =min_time: 18.41521 ms avg_time: 18.77301 ms max_time: 19.02428 ms, AVG Performance:23011.75781 Gflops C[0]: 16949.73047 c[-1]: 16949.73047
M N K = 8192 8192 8192, Time =min_time: 40.06994 ms avg_time: 41.02715 ms max_time: 42.44430 ms, AVG Performance:24959.08594 Gflops C[0]: 22597.73047 c[-1]: 22597.73047
M N K = 12288 12288 12288, Time =min_time: 115.06299 ms avg_time: 116.72612 ms max_time: 118.06106 ms, AVG Performance:29607.76758 Gflops C[0]: 33893.73047 c[-1]: 33893.73047
M N K = 16384 16384 16384, Time =min_time: 303.33020 ms avg_time: 304.75174 ms max_time: 305.86111 ms, AVG Performance:26880.89453 Gflops C[0]: 45189.73047 c[-1]: 45189.730474、LDS.128 float4* 优化
上述代码中每个线程拿4个数据,是采用for循环来实现的,可以进一步采用LDS.128指令来优化,在cuda编程中使用float4命令来告诉编译器该条语句编译成LDS.128,一个线程拿4个数据需要一次指令更加快速。
#define FLOAT4(pointer) (reinterpret_cast<float4*>(&(pointer))[0])
for (int i=0;i<4;i++){
s_a[load_a_sh_m][load_a_sh_k+i] = A[a_gl_adress+i];
}
修改为
FLOAT4(s_a[load_a_sh_m][load_a_sh_k]) = FLOAT4(A[a_gl_adress]);
for (int i=0;i<4;i++){
s_b[load_b_sh_k][load_b_sh_n+i] = B[b_gl_adress+i];
}
修改为
FLOAT4(s_b[load_b_sh_k][load_b_sh_n]) = FLOAT4(B[b_gl_adress]);
for (int i=0; i<4;i++){
C[c_gl_adress+i] = sub_c[m][n+i];
}
修改为
FLOAT4(C[c_gl_adress]) = FLOAT4(sub_c[m][n]);性能继续提升,最大提升10%,结果如下
M N K = 128 128 128, Time =min_time: 0.04106 ms avg_time: 0.68262 ms max_time: 6.44352 ms, AVG Performance: 5.72245 Gflops C[0]: 353.11710 c[-1]: 353.11710
M N K = 192 192 192, Time =min_time: 0.06154 ms avg_time: 0.06422 ms max_time: 0.06697 ms, AVG Performance: 205.27213 Gflops C[0]: 529.67566 c[-1]: 529.67566
M N K = 256 256 256, Time =min_time: 0.07588 ms avg_time: 0.08133 ms max_time: 0.11039 ms, AVG Performance: 384.25708 Gflops C[0]: 706.23425 c[-1]: 706.23425
M N K = 384 384 384, Time =min_time: 0.11252 ms avg_time: 0.12186 ms max_time: 0.15268 ms, AVG Performance: 865.52185 Gflops C[0]: 1059.35071 c[-1]: 1059.35071
M N K = 512 512 512, Time =min_time: 0.17787 ms avg_time: 0.18119 ms max_time: 0.19354 ms, AVG Performance: 1379.79089 Gflops C[0]: 1412.46008 c[-1]: 1412.46008
M N K = 768 768 768, Time =min_time: 0.37560 ms avg_time: 0.39159 ms max_time: 0.40274 ms, AVG Performance: 2154.69067 Gflops C[0]: 2118.68188 c[-1]: 2118.68188
M N K = 1024 1024 1024, Time =min_time: 0.57334 ms avg_time: 0.61253 ms max_time: 0.63785 ms, AVG Performance: 3265.16699 Gflops C[0]: 2824.93188 c[-1]: 2824.93188
M N K = 1536 1536 1536, Time =min_time: 1.47313 ms avg_time: 1.51121 ms max_time: 1.53989 ms, AVG Performance: 4466.62305 Gflops C[0]: 4237.43164 c[-1]: 4237.43164
M N K = 2048 2048 2048, Time =min_time: 2.14897 ms avg_time: 2.25550 ms max_time: 2.34527 ms, AVG Performance: 7093.78613 Gflops C[0]: 5649.93164 c[-1]: 5649.93164
M N K = 3072 3072 3072, Time =min_time: 4.39849 ms avg_time: 4.55569 ms max_time: 4.74102 ms, AVG Performance:11853.32227 Gflops C[0]: 8474.93164 c[-1]: 8474.93164
M N K = 4096 4096 4096, Time =min_time: 7.44929 ms avg_time: 7.65491 ms max_time: 7.91398 ms, AVG Performance:16721.28906 Gflops C[0]: 11299.93164 c[-1]: 11299.93164
M N K = 6144 6144 6144, Time =min_time: 16.54467 ms avg_time: 17.26571 ms max_time: 17.97335 ms, AVG Performance:25020.69727 Gflops C[0]: 16949.73047 c[-1]: 16949.73047
M N K = 8192 8192 8192, Time =min_time: 35.82525 ms avg_time: 37.56758 ms max_time: 38.81329 ms, AVG Performance:27257.54688 Gflops C[0]: 22597.73047 c[-1]: 22597.73047
M N K = 12288 12288 12288, Time =min_time: 107.80151 ms avg_time: 110.40736 ms max_time: 112.49837 ms, AVG Performance:31302.25977 Gflops C[0]: 33893.73047 c[-1]: 33893.73047
M N K = 16384 16384 16384, Time =min_time: 271.26416 ms avg_time: 275.96844 ms max_time: 278.27374 ms, AVG Performance:29684.55469 Gflops C[0]: 45189.73047 c[-1]: 45189.730475、__syncthreads()位置优化
__syncthreads()的位置对代码效率也有一定的影响,上述代码中的第二个同步源语可以放在for循环体开始的地方——因为最后一次的计算完成了就不需要等它其他的线程计算完成;之前的需要等待是因为下一次的计算需要更新shared memory,具有线程依赖性,上一次的计算要用到前一时刻的shared memory的值。
for (int bk=0; bk<(K+BK-1)/BK;bk++){
//等待计算同步的syncthreads源语放到for循环开始的地方
__syncthreads();
//A的所在列
......数据从global memory 加载到 shared memory中
__syncthreads();
#pragma unroll
for(int j=0; j<BK; j++){
#pragma unroll
for(int m=0; m<TM; m++){
#pragma unroll
for(int n=0; n<TN; n++){
// sharedMemory s_a的行 针对不同的线程
int index_a_sh_m = ty*TM + m;
// sharedMemory s_b的列 针对不同的线程
int index_b_sh_n = tx*TN + n;
sub_c[m][n] += s_a[index_a_sh_m][j] * s_b[j][index_b_sh_n];
}
}
}
}效果也有提升,提升0.6-3%不等,结果如下:
M N K = 128 128 128, Time =min_time: 0.03451 ms avg_time: 0.68194 ms max_time: 6.50465 ms, AVG Performance: 5.72812 Gflops C[0]: 353.11710 c[-1]: 353.11710
M N K = 192 192 192, Time =min_time: 0.05140 ms avg_time: 0.05399 ms max_time: 0.05847 ms, AVG Performance: 244.16811 Gflops C[0]: 529.67566 c[-1]: 529.67566
M N K = 256 256 256, Time =min_time: 0.06922 ms avg_time: 0.07027 ms max_time: 0.07260 ms, AVG Performance: 444.73300 Gflops C[0]: 706.23425 c[-1]: 706.23425
M N K = 384 384 384, Time =min_time: 0.09953 ms avg_time: 0.10290 ms max_time: 0.11418 ms, AVG Performance: 1024.95239 Gflops C[0]: 1059.35071 c[-1]: 1059.35071
M N K = 512 512 512, Time =min_time: 0.17705 ms avg_time: 0.18015 ms max_time: 0.18299 ms, AVG Performance: 1387.70959 Gflops C[0]: 1412.46008 c[-1]: 1412.46008
M N K = 768 768 768, Time =min_time: 0.37458 ms avg_time: 0.38070 ms max_time: 0.38523 ms, AVG Performance: 2216.29077 Gflops C[0]: 2118.68188 c[-1]: 2118.68188
M N K = 1024 1024 1024, Time =min_time: 0.58204 ms avg_time: 0.60566 ms max_time: 0.64451 ms, AVG Performance: 3302.20996 Gflops C[0]: 2824.93188 c[-1]: 2824.93188
M N K = 1536 1536 1536, Time =min_time: 1.41229 ms avg_time: 1.44739 ms max_time: 1.47753 ms, AVG Performance: 4663.55859 Gflops C[0]: 4237.43164 c[-1]: 4237.43164
M N K = 2048 2048 2048, Time =min_time: 2.22444 ms avg_time: 2.27107 ms max_time: 2.30205 ms, AVG Performance: 7045.14355 Gflops C[0]: 5649.93164 c[-1]: 5649.93164
M N K = 3072 3072 3072, Time =min_time: 4.38671 ms avg_time: 4.52999 ms max_time: 4.68951 ms, AVG Performance:11920.55078 Gflops C[0]: 8474.93164 c[-1]: 8474.93164
M N K = 4096 4096 4096, Time =min_time: 7.40782 ms avg_time: 7.61178 ms max_time: 7.78086 ms, AVG Performance:16816.04102 Gflops C[0]: 11299.93164 c[-1]: 11299.93164
M N K = 6144 6144 6144, Time =min_time: 16.90030 ms avg_time: 17.21714 ms max_time: 17.72001 ms, AVG Performance:25091.27930 Gflops C[0]: 16949.73047 c[-1]: 16949.73047
M N K = 8192 8192 8192, Time =min_time: 36.12129 ms avg_time: 36.63154 ms max_time: 37.29746 ms, AVG Performance:27954.05078 Gflops C[0]: 22597.73047 c[-1]: 22597.73047
M N K = 12288 12288 12288, Time =min_time: 105.01406 ms avg_time: 106.74062 ms max_time: 108.62878 ms, AVG Performance:32377.55273 Gflops C[0]: 33893.73047 c[-1]: 33893.73047
M N K = 16384 16384 16384, Time =min_time: 271.12808 ms avg_time: 274.21143 ms max_time: 277.60864 ms, AVG Performance:29874.75781 Gflops C[0]: 45189.73047 c[-1]: 45189.73047上面的实现方案,采用了shared Memory对global memory的数据加载进行了优化,减少了重复读取的次数;进一步采用了float4*和__syncthreads()位置更换等技巧进行优化,加速数据的加载速度。同样的上述shared Memory优化方式存在问题,有进一步的提升空间。
6、blank conflict优化
bank概念
在GPU的shared memory硬件设计上,把shared memory的硬件划分为32个子区域,每个区域就是一个bank,同时每个bank可以分为很多层;每个bank的位宽是32位也就是4个字节(byte)。shared memory数据的映射到bank上的规则如下:shared memory上连续的128字节的数据映射到banks上的某一层。比如给定一组单精度数组,0-31号元素按顺序映射到0-31号bank的第一层;32-63号元素映射到0-31号bank的第二层......后续的数据以此类推
bank conflict
简单含义:同一个block中的同一个warp中的线程束中的不同的线程同时访问同一个bank中不同层的数据,这个时候就会产生bank冲突。相反的只要同一个block中的同一个warp中的线程束中的不同的线程不是同时访问同一个bank中不同层的数据,就不会产生bank冲突。小结bank冲突的充要条件:
a、bank 是共享内存中的概念, 只有访问共享内存的前提下才会发生 bank 冲突
b、bank 冲突发生在warp线程束之内, 不同线程束之间不存在 bank 冲突
c、warp线程束的不同线程同时访问同一个bank不同层的数据才会发生bank冲突
从《搞懂 CUDA Shared Memory 上的 bank conflicts 和向量化指令(LDS.128 / float4)的访存特点》
一文中可以得出bank冲突还与向量化指令有关,一个线程访问4bytes、8bytes、以及16bytes的时候,bank冲突的情形是不一样的。具体到memory transaction来说,sharedMemory的一次memory transaction最多只能访问128bytes的数据。一个thread访问4bytes,一次memory transaction需要32个线程来完成,这个时候就需要考虑一个warp中32个线程;一个thread访问8bytes,一次memory transaction需要16个线程来完成,因此需要考虑half-warp中的16个线程,原来的一个warp切分为了2个half-warp,它们访问数据的时候是以half-warp为单位的,只在half-warp中有可能存在bank冲突;一个thread访问16bytes,一次memory transaction需要8个线程来完成,因此需要考虑quarter-warp中的8个线程,原来的一个warp切分为了4个quarter-warp,它们访问数据的时候是以quarter-warp为单位的,只在quarter-warp中有可能存在bank冲突。
bank conflict危害和处理后的收益
bank conflict的危害不言而喻,把原来可以在一次memory transaction一个时钟周期就能完成的任务,变成多次memory transaction在多个不同的时钟周期内串行完成,shared memory访问数据的时钟周期可能成倍增长。如果减少bank conflict甚至消除bank conflict,那么shared memory访问数据的速度会有一定的提升或者极大的提升。
还有一个基础知识点一个warp中的32个线程到底是怎么分配的,一个warp中的线程是连续编号的32个线程,其中线程编号tid=blockDim.x * threadIdx.y+threadIdx.x。
有了以上的bank conflict相关的概念和总结,可以分析上述分块+shared memory版本矩阵乘法算子是否存在bank conflict。
写数据
对于s_a共享内存,其情况如下示意图:

对应代码:
const int tid = blockDim.x * ty + tx;
int load_a_sh_m = tid>>1;
// 被2整除的就是0 不能整除的就是4
int load_a_sh_k = (tid&1)<<2;
for (int bk=0; bk<(K+BK-1)/BK;bk++){
//A的所在列
int load_a_gl_k = load_a_sh_k + bk*BK;
int a_gl_adress = load_a_gl_m * K + load_a_gl_k;
//把A中的以a_gl_adress为起点的4个元素复制到s_a中以[load_a_sh_m]*[load_a_sh_k]为起点的4个地址上
FLOAT4(s_a[load_a_sh_m][load_a_sh_k]) = FLOAT4(A[a_gl_adress]);共享内存在写s_a的时候,每个线程采用float4*一次访问4个float32的数据,因此在考虑bank conflict的时候只需要考虑quarter-warp中的8个线程(这个8个线程构成一个memory transaction一次发射,原始的warp 32个线程的概念变为quarter-warp中的8个线程)。128*8的数据写入sharedMemory中,其bank分布、threads和data分布如上图。bank分布中的数字表示具体的那个bank,bank_layer表示bank的层序号;threads中的th0等表示线程id,一个block有255个线程,8个线程一组,形成一个quarter-warp(比如th0-th7)。一个quarter-warp内的8个线程并没有访问相同的bank中的不同层的数据(th0访问的是bank 0-3的第0层;th7访问的是bank28-31的第0层),因此对于写s_a的时候,sharedMemory不存在bank conflict。至于th8-th15访问了bank0-bank31的第二层,但是这个是其他的warp的线程所以不构成bank conflict。
对于s_b共享内存,其情况如下示意图:

对于8*128的s_b其bank分布、threads和data分布如上图,每一行的128个位置被划分为4层bank(每层0-31号),写数据的时候同样的一个quarter-warp内的8个线程没有访问相同的bank中的不同层的数据(th0访问的是bank 0-3的第0层;th7访问的是bank28-31的第0层,也就是第一行的前32个元素),同理其余的线程以此类推,显而易见的没有构成bank conflict。
读数据
对于从share memory读数据到寄存器进行计算过程中,并没有采用float4*来读取共享内存中的数据,每个线程每次只访问一个数据(float32 4 byte),因此考虑bank冲突的时候需要考虑常规的一个warp中32个线程(一次memory transaction最多支持128 byte数据 32*1*4)的情形。
对应代码:
for(int j=0; j<BK; j++){
#pragma unroll
for(int m=0; m<TM; m++){
#pragma unroll
for(int n=0; n<TN; n++){
// sharedMemory s_a的行 针对不同的线程
int index_a_sh_m = ty*TM + m;
// sharedMemory s_b的列 针对不同的线程
int index_b_sh_n = tx*TN + n;
sub_c[m][n] += s_a[index_a_sh_m][j] * s_b[j][index_b_sh_n];
}
}
}对于s_a的读取,bank、线程分布如下图

对于0-15号线程读取s_a中的前8号8列数据。当不同的线程一个读取前4行(第一层bank)的数据,一个线程读取后4行(第二层bank)的数据且是相同的bank的时候存在bank conflict (这个可能性是存在的,并不一定存在,有可能它们读取数据的时候是同步读取都读相同bank,层数和序号都相同);同样的16-31号线程之间也存在这样的bank conflict;而对于1-15号和16-31号两组线程间,也是存在bank conflict的。后续的线程每32为一组,组内存在bank conflict;组内的子组16个线程也是存在bank conflict。
对于s_b的读取,bank、线程分布如下图

同样的需要考虑一个warp中的32个线程,如图所示每一个线程加载8行8列数据;一行有128个数据,被切分为4层bank。因此0-31号线程中,0-4-8-12存在bank conflict(读取0-7号bank的不同层)、1-5-9-13存在bank conflict(读取8-15号bank的不同层)、2-6-10-14号线程存在bank conflict(读取16-23号bank的不同层)以及3-7-11-15号线程存在bank conflict(读取24-31号bank的不同层)
以上分析了s_a和s_b共享内存在矩阵乘法期间的bank conflict冲突情况,这会导致矩阵乘法的速度比较慢,因此可以想办法优化,减少甚至完全避免bank conflict。
读数据bank conflict的优化
对于s_b,如果采用float4*的形式来加载数据呢?bank conflict 只考虑quarter-warp中的8个线程。bank和thread的访问分布,可以考虑在一个bank layer中用8个线程访问 32个数据,那么就完全不存在bank conflict了。其bank和线程分布如下:

tx=0的线程访问前四列0-3列的数据,和64-67列的数据;tx=1的线程访问4-7的数据以此类推tx=7访问28-32列的数据以及84-87列的数据。由于ty=0的时候tx=0-7是前8个线程在一个quarter-warp中,而这8个线程把一层bank的所有bank的数据全部不重复的访问,因此完全没有bank conflict。不过有一个注意的点tx=0的线程访问前四列0-3列的数据和64-67列的数据的时候是要串行访问的。
所以在实现代码的时候可以考虑把数据从global memory中采用float4*加载到sharedmemory s_b中,同样的采用float4*从sharedmemory s_b中读数据到寄存器中进行计算。
对于s_a而言可以同样的采用上述的s_b的排布,把s_a的排列进行转置,之前是128*8转置为8*128的形式。示意图如下

代码如下
__global__ void matrixMulShareMemoryV2(
float * __restrict__ c, float * __restrict__ a, float * __restrict__ b,
const int M, const int N, const int K) {
// 解决bank冲突
const int BM = 128;
const int BN = 128;
const int BK = 8;
const int TM = 8;
const int TN = 8;
const int bx = blockIdx.x;
const int by = blockIdx.y;
const int tx = threadIdx.x;
const int ty = threadIdx.y;
const int tid = ty * blockDim.x + tx;
__shared__ float s_a[BK][BM];
__shared__ float s_b[BK][BN];
float r_load_a[4];
float r_comp_a[TM];
float r_comp_b[TN];
float r_c[TM][TN] = {0.0};
int load_a_smem_m = tid >> 1;
int load_a_smem_k = (tid & 1) << 2;
int load_b_smem_k = tid >> 5;
int load_b_smem_n = (tid & 31) << 2;
int load_a_gmem_m = by * BM + load_a_smem_m;
int load_b_gmem_n = bx * BN + load_b_smem_n;
for (int bk = 0; bk < (K + BK - 1) / BK; bk++) {
int load_a_gmem_k = bk * BK + load_a_smem_k;
int load_a_gmem_addr = OFFSET(load_a_gmem_m, load_a_gmem_k, K);
int load_b_gmem_k = bk * BK + load_b_smem_k;
int load_b_gmem_addr = OFFSET(load_b_gmem_k, load_b_gmem_n, N);
FLOAT4(r_load_a[0]) = FLOAT4(a[load_a_gmem_addr]);
// s_a按列存储
s_a[load_a_smem_k ][load_a_smem_m] = r_load_a[0];
s_a[load_a_smem_k + 1][load_a_smem_m] = r_load_a[1];
s_a[load_a_smem_k + 2][load_a_smem_m] = r_load_a[2];
s_a[load_a_smem_k + 3][load_a_smem_m] = r_load_a[3];
FLOAT4(s_b[load_b_smem_k][load_b_smem_n]) = FLOAT4(b[load_b_gmem_addr]);
__syncthreads();
#pragma unroll
for (int tk = 0; tk < BK; tk++) {
FLOAT4(r_comp_a[0]) = FLOAT4(s_a[tk][ty * TM / 2 ]);
FLOAT4(r_comp_a[4]) = FLOAT4(s_a[tk][ty * TM / 2 + BM / 2]);
FLOAT4(r_comp_b[0]) = FLOAT4(s_b[tk][tx * TN / 2 ]);
FLOAT4(r_comp_b[4]) = FLOAT4(s_b[tk][tx * TN / 2 + BN / 2]);
#pragma unroll
for (int tm = 0; tm < TM; tm++) {
#pragma unroll
for (int tn = 0; tn < TN; tn++) {
r_c[tm][tn] += r_comp_a[tm] * r_comp_b[tn];
}
}
}
__syncthreads();
}
#pragma unroll
for (int i = 0; i < TM / 2; i++) {
int store_c_gmem_m = by * BM + ty * TM / 2 + i;
int store_c_gmem_n = bx * BN + tx * TN / 2;
int store_c_gmem_addr = OFFSET(store_c_gmem_m, store_c_gmem_n, N);
FLOAT4(c[store_c_gmem_addr]) = FLOAT4(r_c[i][0]);
FLOAT4(c[store_c_gmem_addr + BN / 2]) = FLOAT4(r_c[i][4]);
}
#pragma unroll
for (int i = 0; i < TM / 2; i++) {
int store_c_gmem_m = by * BM + BM / 2 + ty * TM / 2 + i;
int store_c_gmem_n = bx * BN + tx * TN / 2;
int store_c_gmem_addr = OFFSET(store_c_gmem_m, store_c_gmem_n, N);
FLOAT4(c[store_c_gmem_addr]) = FLOAT4(r_c[i + TM / 2][0]);
FLOAT4(c[store_c_gmem_addr + BN / 2]) = FLOAT4(r_c[i + TM / 2][4]);
}
}跑一遍结果,看看性能
M N K = 128 128 128, Time =min_time: 0.03410 ms avg_time: 0.82476 ms max_time: 7.93579 ms, AVG Performance: 4.73622 Gflops C[0]: 353.11710 c[-1]: 353.11710
M N K = 192 192 192, Time =min_time: 0.05192 ms avg_time: 0.05394 ms max_time: 0.05643 ms, AVG Performance: 244.39844 Gflops C[0]: 529.67566 c[-1]: 529.67566
M N K = 256 256 256, Time =min_time: 0.06605 ms avg_time: 0.06782 ms max_time: 0.07178 ms, AVG Performance: 460.78613 Gflops C[0]: 706.23425 c[-1]: 706.23425
M N K = 384 384 384, Time =min_time: 0.10752 ms avg_time: 0.11000 ms max_time: 0.11366 ms, AVG Performance: 958.83472 Gflops C[0]: 1059.35071 c[-1]: 1059.35071
M N K = 512 512 512, Time =min_time: 0.18012 ms avg_time: 0.19387 ms max_time: 0.19784 ms, AVG Performance: 1289.49133 Gflops C[0]: 1412.46008 c[-1]: 1412.46008
M N K = 768 768 768, Time =min_time: 0.34458 ms avg_time: 0.36507 ms max_time: 0.38400 ms, AVG Performance: 2311.21631 Gflops C[0]: 2118.68188 c[-1]: 2118.68188
M N K = 1024 1024 1024, Time =min_time: 0.60631 ms avg_time: 0.62834 ms max_time: 0.64717 ms, AVG Performance: 3182.99902 Gflops C[0]: 2824.93188 c[-1]: 2824.93188
M N K = 1536 1536 1536, Time =min_time: 1.32608 ms avg_time: 1.35953 ms max_time: 1.40554 ms, AVG Performance: 4964.93555 Gflops C[0]: 4237.43164 c[-1]: 4237.43164
M N K = 2048 2048 2048, Time =min_time: 2.10483 ms avg_time: 2.17170 ms max_time: 2.21839 ms, AVG Performance: 7367.50342 Gflops C[0]: 5649.93164 c[-1]: 5649.93164
M N K = 3072 3072 3072, Time =min_time: 4.14700 ms avg_time: 4.22830 ms max_time: 4.36163 ms, AVG Performance:12771.08887 Gflops C[0]: 8474.93164 c[-1]: 8474.93164
M N K = 4096 4096 4096, Time =min_time: 6.56179 ms avg_time: 6.85808 ms max_time: 7.84835 ms, AVG Performance:18664.12500 Gflops C[0]: 11299.93164 c[-1]: 11299.93164
M N K = 6144 6144 6144, Time =min_time: 15.69608 ms avg_time: 16.74945 ms max_time: 17.63256 ms, AVG Performance:25791.88477 Gflops C[0]: 16949.73047 c[-1]: 16949.73047
M N K = 8192 8192 8192, Time =min_time: 33.82498 ms avg_time: 35.62038 ms max_time: 36.52895 ms, AVG Performance:28747.58398 Gflops C[0]: 22597.73047 c[-1]: 22597.73047
M N K = 12288 12288 12288, Time =min_time: 99.23318 ms avg_time: 99.87777 ms max_time: 100.68797 ms, AVG Performance:34602.29688 Gflops C[0]: 33893.73047 c[-1]: 33893.73047
M N K = 16384 16384 16384, Time =min_time: 267.60837 ms avg_time: 270.86102 ms max_time: 273.63031 ms, AVG Performance:30244.29102 Gflops C[0]: 45189.73047 c[-1]: 45189.73047上述代码中对于s_a写数据仍然存在bank conflict,这里不再继续详细分析了。看看这个版本提速效果,提升1-10.8%左右。相对理论性能,还有有差距,还有优化的空间。
7、流水并行化——Double Buffering
先分析上述最优版本也就是解决了bank conflict版本代码的核心流程,如下示意图:

那么大的for循环中的计算流程:访存0(可细分为GM到RE访存和RE到SM访存)→计算0→访存1→计算1→......访存n→计算n
上述的计算流程是串行的,并且访存耗时比较长,那么有没有方案改变上述存串行的计算流程进一步提升运算效率呢?那么就是下面说的double buffering这个技巧了。double buffering顾名思义就是采用两份缓存使得 访存-计算 串行的模式进化为流水线的方式。

上图就是一个简单的对比(图中是认为load耗时比较长,comp耗时比较短),图中的double buffer中comp0和load1是并行进行的,节约了一定的时间,明显最后经过同样的计算过程后,double buffer完成计算的耗时要短。代码如何实现呢?
第一、要开启两个share memory,分别用于当前轮次的数据存储和下一轮的数据存储
第二、__syncthreads也只需要一个了,因为当前轮的计算和下一轮数据的加载是独立分开的,就不需要想之前的版本,都使用同一个share memory,所有线程往其中写数据,要同步一次;等所有线程写完以后才能开启计算。计算的时候又需要同步一次,需要等所有的线程计算完毕后,才能更新share memory中的数据。核心逻辑代码如下:
{
int load_a_gmem_k = load_a_smem_k;
int load_a_gmem_addr = OFFSET(load_a_gmem_m, load_a_gmem_k, K);
int load_b_gmem_k = load_b_smem_k;
int load_b_gmem_addr = OFFSET(load_b_gmem_k, load_b_gmem_n, N);
FLOAT4(r_load_a[0]) = FLOAT4(a[load_a_gmem_addr]);
FLOAT4(r_load_b[0]) = FLOAT4(b[load_b_gmem_addr]);
s_a[0][load_a_smem_k ][load_a_smem_m] = r_load_a[0];
s_a[0][load_a_smem_k + 1][load_a_smem_m] = r_load_a[1];
s_a[0][load_a_smem_k + 2][load_a_smem_m] = r_load_a[2];
s_a[0][load_a_smem_k + 3][load_a_smem_m] = r_load_a[3];
FLOAT4(s_b[0][load_b_smem_k][load_b_smem_n]) = FLOAT4(r_load_b[0]);
}
for (int bk = 1; bk < (K + BK - 1) / BK; bk++) {
__syncthreads();
int smem_sel = (bk - 1) & 1;
int smem_sel_next = bk & 1;
int load_a_gmem_k = bk * BK + load_a_smem_k;
int load_a_gmem_addr = OFFSET(load_a_gmem_m, load_a_gmem_k, K);
int load_b_gmem_k = bk * BK + load_b_smem_k;
int load_b_gmem_addr = OFFSET(load_b_gmem_k, load_b_gmem_n, N);
FLOAT4(r_load_a[0]) = FLOAT4(a[load_a_gmem_addr]);
FLOAT4(r_load_b[0]) = FLOAT4(b[load_b_gmem_addr]);
#pragma unroll
for (int tk = 0; tk < BK; tk++) {
FLOAT4(r_comp_a[0]) = FLOAT4(s_a[smem_sel][tk][ty * TM / 2 ]);
FLOAT4(r_comp_a[4]) = FLOAT4(s_a[smem_sel][tk][ty * TM / 2 + BM / 2]);
FLOAT4(r_comp_b[0]) = FLOAT4(s_b[smem_sel][tk][tx * TN / 2 ]);
FLOAT4(r_comp_b[4]) = FLOAT4(s_b[smem_sel][tk][tx * TN / 2 + BN / 2]);
#pragma unroll
for (int tm = 0; tm < TM; tm++) {
#pragma unroll
for (int tn = 0; tn < TN; tn++) {
r_c[tm][tn] += r_comp_a[tm] * r_comp_b[tn];
}
}
}
s_a[smem_sel_next][load_a_smem_k ][load_a_smem_m] = r_load_a[0];
s_a[smem_sel_next][load_a_smem_k + 1][load_a_smem_m] = r_load_a[1];
s_a[smem_sel_next][load_a_smem_k + 2][load_a_smem_m] = r_load_a[2];
s_a[smem_sel_next][load_a_smem_k + 3][load_a_smem_m] = r_load_a[3];
FLOAT4(s_b[smem_sel_next][load_b_smem_k][load_b_smem_n]) = FLOAT4(r_load_b[0]);
}
// 最后一次的计算
#pragma unroll
for (int tk = 0; tk < BK; tk++) {
FLOAT4(r_comp_a[0]) = FLOAT4(s_a[1][tk][ty * TM / 2 ]);
FLOAT4(r_comp_a[4]) = FLOAT4(s_a[1][tk][ty * TM / 2 + BM / 2]);
FLOAT4(r_comp_b[0]) = FLOAT4(s_b[1][tk][tx * TN / 2 ]);
FLOAT4(r_comp_b[4]) = FLOAT4(s_b[1][tk][tx * TN / 2 + BN / 2]);
#pragma unroll
for (int tm = 0; tm < TM; tm++) {
#pragma unroll
for (int tn = 0; tn < TN; tn++) {
r_c[tm][tn] += r_comp_a[tm] * r_comp_b[tn];
}
}
}从代码上来看,程序执行还是顺序执行的,比较难易理解为啥会节约时间,得到优化。这里需要对GPU中的底层指令有一定的基础知识,我这边也是看了很多博客的解释才稍微了解其中的奥妙。

还是以这张图来说明,cuda代码中如图的代码,可以把代码执行的顺序理解为访存指令0、访存指令1和计算指令2这样顺序进行指令的发射然后完成的。同时注意到访存指令和计算指令对应GPU中不同的硬件,它们本身是可以并行的。代码中一些列指令(代码排序了的)执行需要有一定的规则:
a、下一个指令需要等上一个指令发射(lauch)后才能进行发射
b、指令具有数据依赖的时候必须到上一个指令发射并完成对应功能后,才能完成下一个指令的发射
c、指令没有数据依赖的时候,相邻的两个指令,上一个指令发射后,不用等到上一个完成对应功能后,可以立即发射下一个指令
对于上述的矩阵计算(无double buffering版本)过程的一轮迭代中,访存指令0和访存指令1 它们之间是存在数据依赖的,因此必须是访存指令0发射并把数据从global memory加载到寄存器中(这个需要耗时的,耗时比较长),然后指令2才能反射。对于访存指令1和计算指令2它们仍然是有数据依赖的,因此要等指令1才能反射,并把寄存器中的数据写到share memory中(这个也是有耗时的,耗时稍短),计算指令2才能进行(完成也要一定的耗时)发射。要等计算指令2完成后,才能开启下一轮的迭代。
而对于有double buffering的版本,指令简示图如下:

由于采用了2个share memory,当前轮计算的数据和访存的数据是不同的数据,不存在数据依赖性。当以访存指令1、计算指令2和访存指令3的顺序排布的时候,指令1和计算指令2是数据无关的,那么当访存指令1发射以后,计算指令2不需要等待访存指令1完成写数据可以立马发射;以访存指令1和访存指令3是存在数据依赖性的,会等待访存指令1完成写数据后才会发射访存指令3。这个过程中相比较无double buffering版本,把计算指令2的耗时给掩盖了。
假如把访存指令3的代码往前挪动(称之为fake double buffering),还是和之前的无double buffering 版本一样,可以对比下效果。
fake double buffering
M N K = 128 128 128, Time =min_time: 0.02181 ms avg_time: 1.20060 ms max_time: 11.80539 ms, AVG Performance: 3.25359 Gflops C[0]: 353.11710 c[-1]: 353.11710
M N K = 192 192 192, Time =min_time: 0.03256 ms avg_time: 0.03394 ms max_time: 0.03543 ms, AVG Performance: 388.41077 Gflops C[0]: 529.67566 c[-1]: 529.67566
M N K = 256 256 256, Time =min_time: 0.04762 ms avg_time: 0.05281 ms max_time: 0.05796 ms, AVG Performance: 591.77002 Gflops C[0]: 706.23425 c[-1]: 706.23425
M N K = 384 384 384, Time =min_time: 0.08417 ms avg_time: 0.11468 ms max_time: 0.16291 ms, AVG Performance: 919.71716 Gflops C[0]: 1059.35071 c[-1]: 1059.35071
M N K = 512 512 512, Time =min_time: 0.15268 ms avg_time: 0.15650 ms max_time: 0.16220 ms, AVG Performance: 1597.45886 Gflops C[0]: 1412.46008 c[-1]: 1412.46008
M N K = 768 768 768, Time =min_time: 0.33126 ms avg_time: 0.34764 ms max_time: 0.37560 ms, AVG Performance: 2427.09546 Gflops C[0]: 2118.68188 c[-1]: 2118.68188
M N K = 1024 1024 1024, Time =min_time: 0.35789 ms avg_time: 0.46844 ms max_time: 0.57272 ms, AVG Performance: 4269.50488 Gflops C[0]: 2824.93188 c[-1]: 2824.93188
M N K = 1536 1536 1536, Time =min_time: 0.80783 ms avg_time: 0.89210 ms max_time: 1.35260 ms, AVG Performance: 7566.42871 Gflops C[0]: 4237.43164 c[-1]: 4237.43164
M N K = 2048 2048 2048, Time =min_time: 1.33263 ms avg_time: 1.50349 ms max_time: 2.11610 ms, AVG Performance:10641.91211 Gflops C[0]: 5649.93164 c[-1]: 5649.93164
M N K = 3072 3072 3072, Time =min_time: 4.05156 ms avg_time: 4.36065 ms max_time: 5.37825 ms, AVG Performance:12383.46777 Gflops C[0]: 8474.93164 c[-1]: 8474.93164
M N K = 4096 4096 4096, Time =min_time: 6.40307 ms avg_time: 6.71478 ms max_time: 7.56245 ms, AVG Performance:19062.43359 Gflops C[0]: 11299.93164 c[-1]: 11299.93164
M N K = 6144 6144 6144, Time =min_time: 14.97477 ms avg_time: 15.94597 ms max_time: 17.13531 ms, AVG Performance:27091.49219 Gflops C[0]: 16949.73047 c[-1]: 16949.73047
M N K = 8192 8192 8192, Time =min_time: 33.06015 ms avg_time: 35.08706 ms max_time: 38.28961 ms, AVG Performance:29184.54883 Gflops C[0]: 22597.73047 c[-1]: 22597.73047
M N K = 12288 12288 12288, Time =min_time: 98.18726 ms avg_time: 99.15405 ms max_time: 102.40656 ms, AVG Performance:34854.85156 Gflops C[0]: 33893.73047 c[-1]: 33893.73047
M N K = 16384 16384 16384, Time =min_time: 260.16675 ms avg_time: 264.75137 ms max_time: 270.67575 ms, AVG Performance:30942.23828 Gflops C[0]: 45189.73047 c[-1]: 45189.73047 real double buffering
M N K = 128 128 128, Time =min_time: 0.02816 ms avg_time: 1.11958 ms max_time: 10.93622 ms, AVG Performance: 3.48903 Gflops C[0]: 353.11710 c[-1]: 353.11710
M N K = 192 192 192, Time =min_time: 0.04362 ms avg_time: 0.04714 ms max_time: 0.06532 ms, AVG Performance: 279.64331 Gflops C[0]: 529.67566 c[-1]: 529.67566
M N K = 256 256 256, Time =min_time: 0.05919 ms avg_time: 0.06265 ms max_time: 0.07946 ms, AVG Performance: 498.82642 Gflops C[0]: 706.23425 c[-1]: 706.23425
M N K = 384 384 384, Time =min_time: 0.08796 ms avg_time: 0.09073 ms max_time: 0.09359 ms, AVG Performance: 1162.38989 Gflops C[0]: 1059.35071 c[-1]: 1059.35071
M N K = 512 512 512, Time =min_time: 0.14397 ms avg_time: 0.15401 ms max_time: 0.18381 ms, AVG Performance: 1623.26196 Gflops C[0]: 1412.46008 c[-1]: 1412.46008
M N K = 768 768 768, Time =min_time: 0.32419 ms avg_time: 0.34297 ms max_time: 0.37304 ms, AVG Performance: 2460.14453 Gflops C[0]: 2118.68188 c[-1]: 2118.68188
M N K = 1024 1024 1024, Time =min_time: 0.49942 ms avg_time: 0.59350 ms max_time: 0.67953 ms, AVG Performance: 3369.82080 Gflops C[0]: 2824.93188 c[-1]: 2824.93188
M N K = 1536 1536 1536, Time =min_time: 1.28512 ms avg_time: 1.36417 ms max_time: 1.55065 ms, AVG Performance: 4948.04688 Gflops C[0]: 4237.43164 c[-1]: 4237.43164
M N K = 2048 2048 2048, Time =min_time: 0.99225 ms avg_time: 1.99034 ms max_time: 2.34681 ms, AVG Performance: 8038.83691 Gflops C[0]: 5649.93164 c[-1]: 5649.93164
M N K = 3072 3072 3072, Time =min_time: 3.89243 ms avg_time: 4.00537 ms max_time: 4.08545 ms, AVG Performance:13481.90918 Gflops C[0]: 8474.93164 c[-1]: 8474.93164
M N K = 4096 4096 4096, Time =min_time: 6.17728 ms avg_time: 6.44715 ms max_time: 6.99494 ms, AVG Performance:19853.71875 Gflops C[0]: 11299.93164 c[-1]: 11299.93164
M N K = 6144 6144 6144, Time =min_time: 14.58186 ms avg_time: 15.45100 ms max_time: 16.53637 ms, AVG Performance:27959.35742 Gflops C[0]: 16949.73047 c[-1]: 16949.73047
M N K = 8192 8192 8192, Time =min_time: 33.41762 ms avg_time: 34.58893 ms max_time: 37.08314 ms, AVG Performance:29604.84766 Gflops C[0]: 22597.73047 c[-1]: 22597.73047
M N K = 12288 12288 12288, Time =min_time: 95.52925 ms avg_time: 99.07566 ms max_time: 103.97993 ms, AVG Performance:34882.43359 Gflops C[0]: 33893.73047 c[-1]: 33893.73047
M N K = 16384 16384 16384, Time =min_time: 252.87250 ms avg_time: 258.88806 ms max_time: 262.78308 ms, AVG Performance:31643.01953 Gflops C[0]: 45189.73047 c[-1]: 45189.73047可以看看它们之间的对比效果

说明在大多数场景下,该方案是有效的,有些维度却是fake double buffering效率更高,感觉不是很理解,说明real double buffering版本在某些维度下访存处理有问题,导致计算效率变低。
8、cublas
cublas计算效率比较高,下面将讲解cublas怎么进行sgemm的。直接看英伟达的cuda cublas doc中的API



参数释义在上图,就不意义解读了。有几个必须要注意的点我们在C++中的GPU内存中的矩阵是按照行进行存储的,而在cublas接受数据后会自动转为按列存储。因此按照:
*A = A[M,K] 、 B*=B[K,N]、*C=[M,N]、transa=CUBLAS_OP_N
进行输入,它们会在GPU自动转化*A = A[K,M] 、 B*=B[N,K]、*C=[N,M],根本就不能正常计算。
因此如果想要实现CPU中C[M,N]=A[M,K]*B[K,N],cublas的参数就得这样设计
*A=B[K,N]、B*=A[M,K]、*C=[M,N]、transa=CUBLAS_OP_N GPU中转化后
*A=B[N,K]、B*=A[K,M]、*C=[N,M]
*C=[N,M]转移到CPU就恢复到*C=[M,N]了
size_t size_a = M * K * sizeof(float);
size_t size_b = K * N * sizeof(float);
size_t size_c = M * N * sizeof(float);
float *d_a, *d_b, *d_c;
// cudaMalloc(&d_a, size_a);
// cudaMalloc(&d_b, size_b);
// cudaMalloc(&d_c, size_c);
cudaMallocManaged(&d_a, size_a);
cudaMallocManaged(&d_b, size_b);
cudaMallocManaged(&d_c, size_c);
matrix_init(1.23456789, d_a, M, K);
matrix_init(2.23456789, d_b, K, N);
matrix_init(0.0, d_c, M, N);
cublasHandle_t cublas_handle;
cublasCreate(&cublas_handle);
float cublas_alpha = 1.0;
float cublas_beta = 0;
cudaEvent_t start, end;
cudaEventCreate(&start);
cudaEventCreate(&end);
cudaEventRecord(start);
for (int i = 0; i < repeat; i++) {
cublasSgemm(cublas_handle, CUBLAS_OP_N, CUBLAS_OP_N, N, M, K, &cublas_alpha, d_b, N, d_a, K, &cublas_beta, d_c, N);
}
cudaEventRecord(end);
cudaEventSynchronize(end);编译的时候
nvcc matrix_2d_mul_cuda_cublas.cu -lcublas -o matrix_2d_mul_cuda_cublas性能结果如下
M N K = 128 128 128, Time =min_time: 0.03042 ms avg_time: 0.89449 ms max_time: 8.58522 ms, AVG Performance: 4.36704 Gflops C[0]: 353.11691 c[-1]: 353.11691
M N K = 192 192 192, Time =min_time: 0.04065 ms avg_time: 0.39824 ms max_time: 3.41903 ms, AVG Performance: 33.10432 Gflops C[0]: 529.67529 c[-1]: 529.67529
M N K = 256 256 256, Time =min_time: 0.08878 ms avg_time: 0.10231 ms max_time: 0.14520 ms, AVG Performance: 305.45068 Gflops C[0]: 706.23370 c[-1]: 706.23370
M N K = 384 384 384, Time =min_time: 0.09759 ms avg_time: 0.10083 ms max_time: 0.10865 ms, AVG Performance: 1045.97168 Gflops C[0]: 1059.35120 c[-1]: 1059.35120
M N K = 512 512 512, Time =min_time: 0.13619 ms avg_time: 0.14607 ms max_time: 0.16671 ms, AVG Performance: 1711.51111 Gflops C[0]: 1412.46838 c[-1]: 1412.46838
M N K = 768 768 768, Time =min_time: 0.37335 ms avg_time: 0.40678 ms max_time: 0.42414 ms, AVG Performance: 2074.19336 Gflops C[0]: 2118.70142 c[-1]: 2118.70142
M N K = 1024 1024 1024, Time =min_time: 0.50709 ms avg_time: 0.81446 ms max_time: 3.47566 ms, AVG Performance: 2455.61523 Gflops C[0]: 2824.93188 c[-1]: 2824.93188
M N K = 1536 1536 1536, Time =min_time: 1.03455 ms avg_time: 1.26659 ms max_time: 1.36714 ms, AVG Performance: 5329.25098 Gflops C[0]: 4237.40527 c[-1]: 4237.40527
M N K = 2048 2048 2048, Time =min_time: 2.08538 ms avg_time: 2.17730 ms max_time: 2.29007 ms, AVG Performance: 7348.54980 Gflops C[0]: 5649.84033 c[-1]: 5649.84033
M N K = 3072 3072 3072, Time =min_time: 3.91537 ms avg_time: 4.05198 ms max_time: 4.33070 ms, AVG Performance:13326.82227 Gflops C[0]: 8474.79590 c[-1]: 8474.79590
M N K = 4096 4096 4096, Time =min_time: 6.77897 ms avg_time: 6.88863 ms max_time: 6.96904 ms, AVG Performance:18581.33594 Gflops C[0]: 11299.79590 c[-1]: 11299.79590
M N K = 6144 6144 6144, Time =min_time: 14.36170 ms avg_time: 15.83771 ms max_time: 16.99943 ms, AVG Performance:27276.66406 Gflops C[0]: 16949.73047 c[-1]: 16949.73047
M N K = 8192 8192 8192, Time =min_time: 28.72248 ms avg_time: 30.71495 ms max_time: 31.80657 ms, AVG Performance:33338.81641 Gflops C[0]: 22597.73047 c[-1]: 22597.73047
M N K = 12288 12288 12288, Time =min_time: 87.88601 ms avg_time: 88.61835 ms max_time: 89.36192 ms, AVG Performance:38998.69531 Gflops C[0]: 33893.73047 c[-1]: 33893.73047
M N K = 16384 16384 16384, Time =min_time: 195.16467 ms avg_time: 196.24759 ms max_time: 196.93333 ms, AVG Performance:41743.18750 Gflops C[0]: 45189.73047 c[-1]: 45189.73047把上述avg performence放在一起得到表格和柱状图,python脚本如下:
from glob import glob
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from plottable import Table, ColumnDefinition
def readtxt(path):
with open(path, 'r', encoding='utf-8') as f:
lines = f.readlines()
res = []
for line in lines:
line = line.split(":")
line = line[4].split(" ")
while "" in line:
line.remove("")
num = round(float(line[0]), 0)
num = int(num)
res.append(num)
return res
if __name__ == '__main__':
paths = glob("./*.txt")
paths.sort()
perferences = []
for path in paths:
if "1_share_0_one_element.txt" not in path and "5_share_memory_v2_bankconflict_reduce.txt" not in path:
perference = readtxt(path)
perferences.append(perference)
print(len(perferences))
mnks = [128, 192, 256, 384, 512, 768, 1024, 1536, 2048, 3072, 4096, 6144, 8192, 12288, 16384]
perferences_dict_cloumn = {}
for i in range(len(perferences[0])):
for ele in perferences:
if str(mnks[i]) not in perferences_dict_cloumn:
perferences_dict_cloumn[str(mnks[i])] = [ele[i]]
else:
perferences_dict_cloumn[str(mnks[i])].append(ele[i])
print(perferences_dict_cloumn)
df = pd.DataFrame()
max_cloumn_index = {}
for k, v in perferences_dict_cloumn.items():
df[k] = v
max_v = max(v)
index = v.index(max_v)
max_cloumn_index[k] = index
print(len(perferences))
fig = plt.figure(figsize=(16, 12), dpi=100)
# 柱状图 子图
ax_bar = fig.add_subplot(211)
# 设置柱体样式
labels = ["naive", "smem_unfloat4", "smem_float4", "sync_change", "bankconflict_reduce", "fake_double_buffering",
"real_double_buffer", "cublas"]
x = np.arange(len(perferences[0]) * 4, step=4)
# 设置柱体宽度
total_width, n = 3, len(labels)
width = total_width / n
x = x - (total_width - width) / n
colors = ["blue", "orange", "green", "yellow", "purple", "brown", "black", "red"]
# 横坐标文字
tick_label = [128, 192, 256, 384, 512, 768, 1024, 1536, 2048, 3072, 4096, 6144, 8192, 12288, 16384]
for i in range(len(perferences)):
ax_bar.bar(x + i * width, perferences[i], width=width, fc=colors[i], align='edge', label=str(labels[i]))
# ax_bar.xticks([ele+3*width for ele in x],tick_label)
ax_bar.set_xticks([ele + 3 * width for ele in x], tick_label)
# 设置标题
ax_bar.set_title("4090 matrix_2d_perfencemence", fontsize=16)
# 设置坐标轴名称
ax_bar.set_xlabel("DIM M=K=N")
ax_bar.set_ylabel("GFLOPS")
# 设置图注
ax_bar.legend()
# 表格子图
ax_table = fig.add_subplot(212)
# 创建表格
df['algorithm'] = labels
df = df.set_index("algorithm")
table = Table(df, column_definitions=[ ColumnDefinition(name=column, textprops={"ha": "left"}) for column in df.columns.tolist()])
# 显示图表
plt.tight_layout() # 调整子图间距
plt.savefig("4090_matrix_2d_perfencemence.jpg")
结果如下

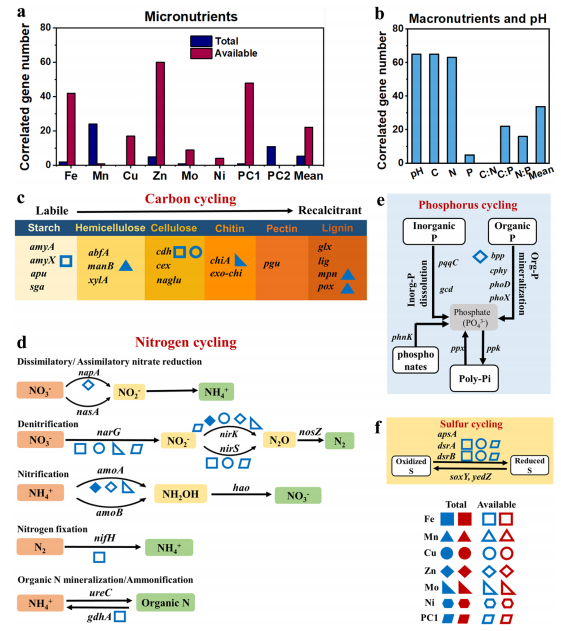
可以看到某些维度上(m=n=k=384、768、1024、2048、3072、4096、6144等维度,图中的黑色矩形长条)上述的方案中的Double Buffering超过了cublas的性能,而在极大矩阵(m=n=k=8192、12288、16384等维度)上达到了cublas的89.44%的性能。还有个比较难以理解的点就是fake dobule buffering(棕色矩形长条)要超出cublas很多,这个就比较奇怪了,有大神可以帮忙解释一下。
由于工作阶段性的繁忙,前前后后断断续续的花了差不多一个月的时间才把这个博客完成,有很多知识有些忘记了,有些需要再次实验验证。不过好在辛苦没有白费,这篇博客,把我知道的关于矩阵计算的相关加速方案以及GPU的一些基础知识点结合起来,能够自圆其说也算是可以分享给大家了,后续有时间继续完成之前的flag!
参考文章
CUDA SGEMM矩阵乘法优化笔记——从入门到cublas
CUDA单精度矩阵乘法(sgemm)优化笔记
CUDA(三):通用矩阵乘法:从入门到熟练
矩阵乘法的 CUDA 实现、优化及性能分析
CUDA 修炼笔记(十) -- Bank
GPU编程8:全局内存3.1→对齐与合并访问
搞懂 CUDA Shared Memory 上的 bank conflicts 和向量化指令(LDS.128 / float4)的访存特点
docs.nvidia.com/cuda/cublas