0. 前言

本文主要记录课程《自动驾驶预测与决策技术》的学习过程，难免会有很多纰漏，感谢指正。
课程链接：https://www.shenlanxueyuan.com/my/course/700
Part1_自动驾驶决策规划简介
Part2_基于模型的预测方法
Part3_路径与轨迹规划

1. 时空联合规划的基本概念

思考： 如何解决窄道会车问题？

问题难点：存在交互，对手车与自车的行为紧密结合。

时空解耦的方法：先生成路径，很难考虑动态障碍物，会生成穿过目标车的轨迹。 然后进行速度规划，由于有障碍物，会进行刹车。解耦实际是为了 减小求解空间，减少算力。

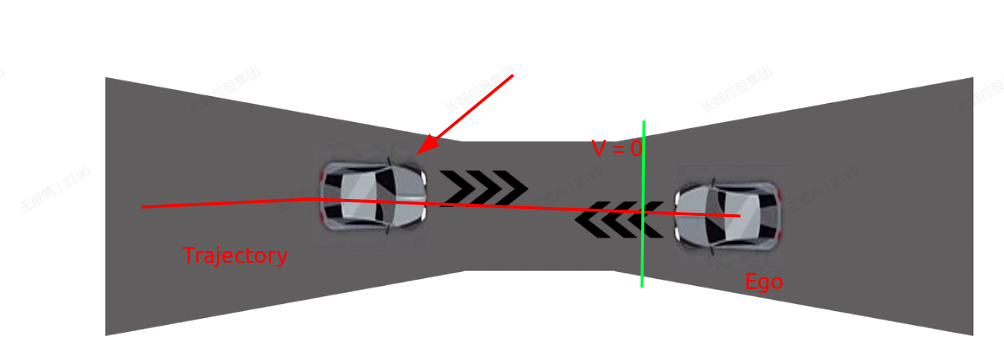
时空联合规划方法：

1. 减速，靠边并让出一部分空间 --> 让。

2. 认为对手车会让行，快速切过去 --> 抢。

1.1 时空分离方法

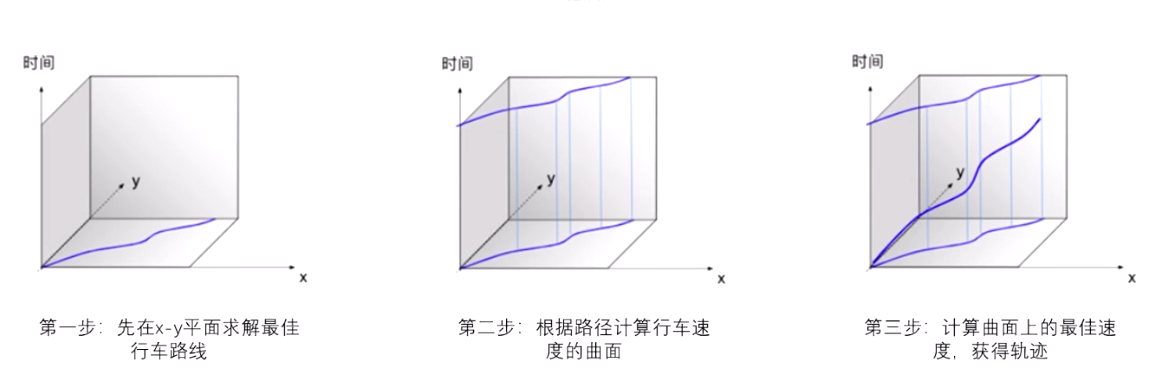
局限性：初始路径决定了轨迹的求解质量，会存在偶发的误制动。在生成轨迹的时候，未考虑障碍物未来一段时间的变化。

1.2 时空联合方法

在 $x-y-t$ 坐标下，或者$s-l-t$坐标下，直接求解轨迹。

问题： 如何求解？

难点：

1. 计算复杂度：空间维度提升，dimension。高维，非凸。 横向绕过，或者纵向加减速，抢让。
2. 交互： 其他障碍物按照预测线去投影，而预测轨迹并完全准确。会跟随本车的动作，自车执行动作，对手车也会变化，障碍物越复杂。指数上升。 暴力方法，不适用于障碍物的交互。

2.基于搜索的时空联合规划 （Hybrid A* ）

2.1 基于Hybrid A* 的时空联合规划建模

• x-y-t : 规划适合场景：路口、半结构化场景（停车场）、非结构化道路（乡间小路）。 无图会依靠x-y-t 。
• s-l-t ：非路口、有明确道路指引、有明确道路结构。

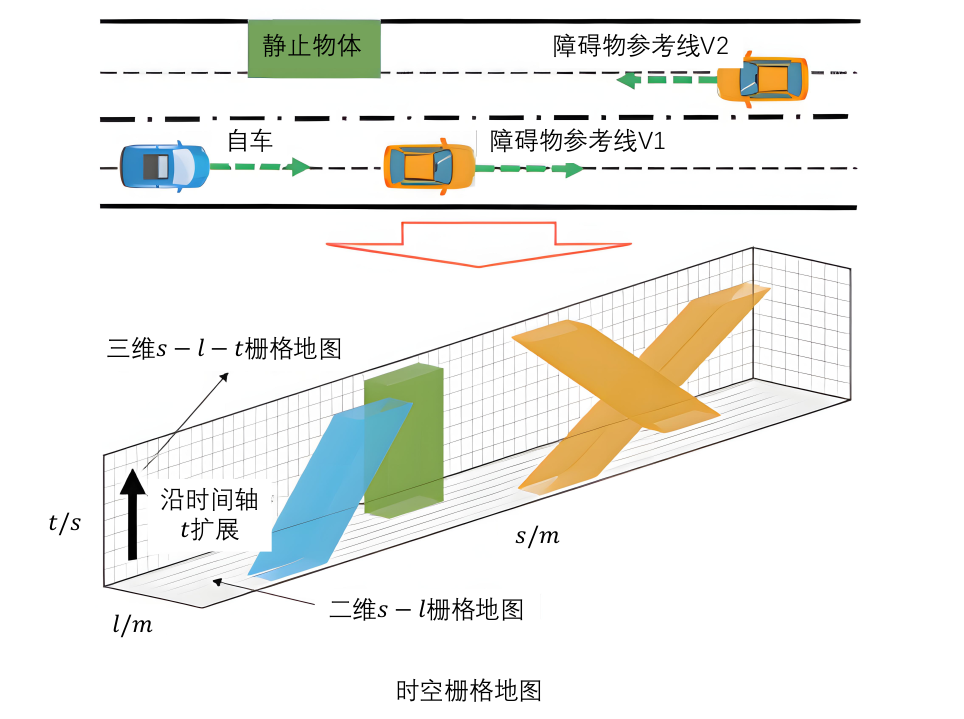
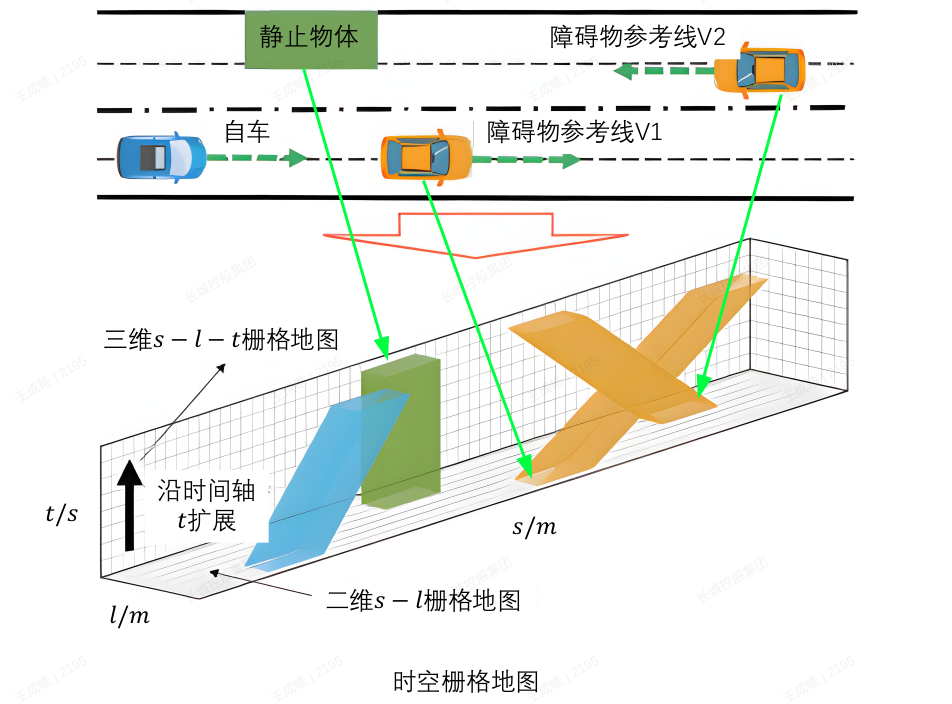
障碍物在三维$s-l-t$ 栅格地图中的投影表示了它在不同时间和位置上的状态，：

1. X-Y-Z 视角

   • 在传统的道路坐标系中，障碍物（例如静止物体和其他车辆）以横向和纵向的空间位置来表示。
   • 图中的静止物体位于最上方，橙色的车辆 分别位于不同的车道上，代表动态障碍物。
   • 这里车辆（或障碍物）在 X、Y 维度上呈现的是物理上的空间位置，反映它们在道路上的横向（车道）和纵向（前后位置）信息。

2. S-L-T 视角

   • S（纵向位置）: 在 SLT 坐标系中，S 代表车辆在道路上的前进距离（也称纵向位置）。图中的 V1 和 V2 的 S 轴值对应它们在道路上的前进距离。

   • L（横向位置）: L 代表车辆在道路上的车道位置，或者横向偏移。这里图中展示了两个动态障碍物分别位于不同的车道，说明它们的 L 值不同。

   • T（时间）: T 轴代表时间，在规划中表示车辆在某个时间点的位置。通过将障碍物在时间维度上延展，展示其随时间的运动轨迹。

   • 静止物体 ：在三维 SLT栅格图中，它在时间轴（T）上并没有延展，因为它是静止的，纵向位置（S）保持不变，横向位置（L）也固定。

   • 动态障碍物：在时间轴上有一定的延展，形成了一条倾斜的轨迹，表示它们随着时间的变化而前进。

3. 障碍物的投影

   • 在SLT图中，橙色车辆的轨迹在时间维度上延展为一个“斜坡状”图形，反映它们在未来的时刻可能出现在的位置。
   • 动态障碍物的轨迹在时间轴（T）上向前倾斜，反映它们随时间的运动变化，而静止物体的轨迹是垂直的，因为它不会随时间移动。

2.2 构建三维时空联合地图

先建立二维图层，然后沿时间轴拓展为三维时空地图。

参考 EPSILON --> SSC 部分代码，xyt -> slt的投影，以及构建slt map.

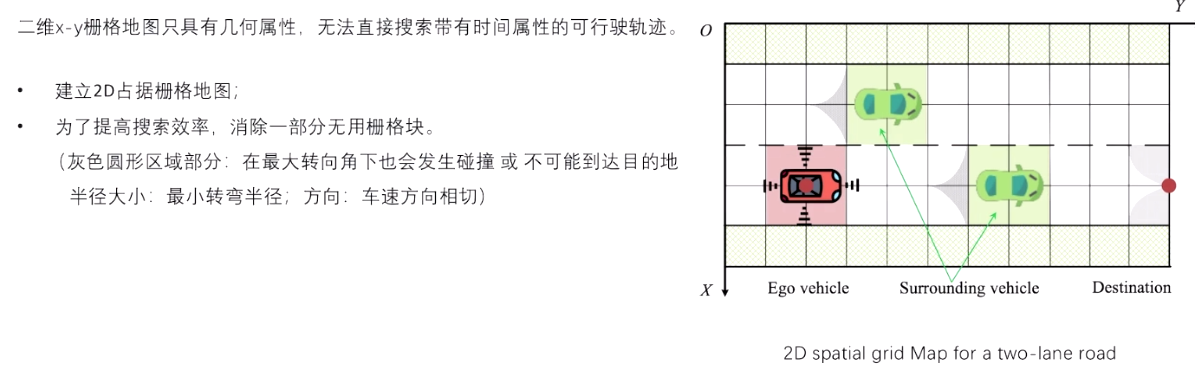
二维栅格沿时间轴拓展生成为三维时空地图。

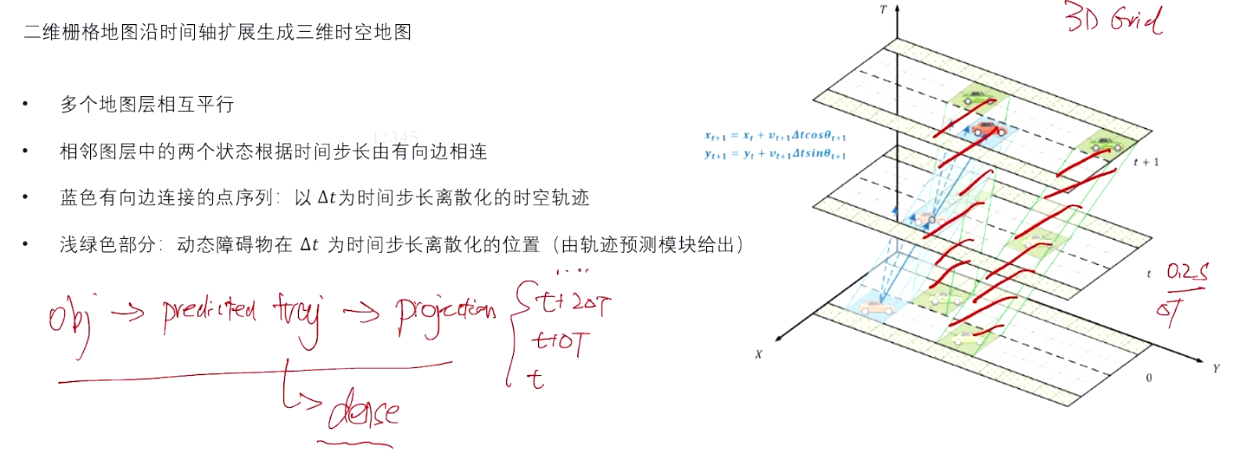
• 为了引入时间维度，在二维地图的基础上，沿着时间轴（T 轴）扩展，生成多个时间层。每个时间层对应一个时间步（如 $(t_0)$, $(t_1)$, $(t_2)$ 等）。

• 每个时间层之间的节点是通过空间位置的连续性连接的，即在每个时间层中，障碍物的位置会随着时间的变化而更新。障碍物的动态信息则通过预测模型（如速度、加速度等）进行计算，生成其在未来时间的预期位置。

• 三维地图中的每一层代表一个时间点，层与层之间相互连接，形成一条时间序列轨迹。车辆通过这一轨迹可以在 (X-Y-T) 三维空间中进行移动。

• 图中展示了浅绿色的障碍物预测轨迹，这表示动态障碍物会随着时间的推移占据不同的位置，影响路径规划。

如何求解：

自车位置–> 搜索的起点，将车辆运动学信息进行离散化、拓展，得到动作空间，根据动作空间扩展时空地图。

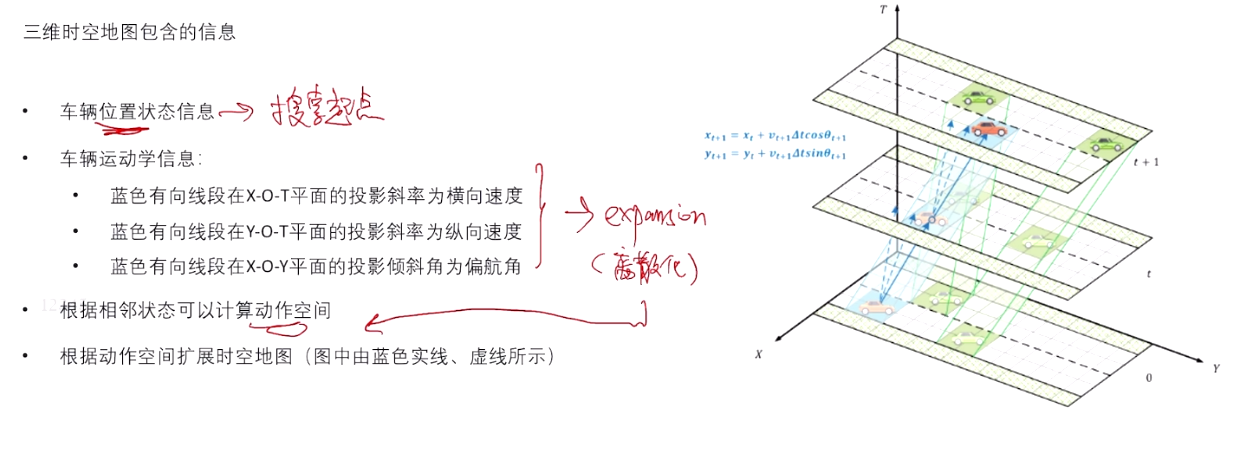
2.3 基于Hybrid A*的时空节点扩展

通过离散曲率（前轮转角）与离散加速度（Acc）得到状态更新方程。

2.4 Hybrid A* ：时空节点启发式函数设计

slt 是个有向图。 不存在倒车的可能，时间无法倒流。

2.5 Hybrid A* ：时空节点成本函数设计

2.6 Hybrid A* 生成参考轨迹

2.6.1 基本步骤

基于 Hybrid A* 算法在时空联合空间中找到轨迹的步骤，，具体可以分为以下几个步骤：

1. 初始条件设置

   • 输入：一个时空联合的有向无环图 (DAG)，它将当前环境和障碍物的动态信息都包含在内。
   • 输出：从起始位置到目标位置的最优时空轨迹。
   • 初始化：
     • 初始化轨迹集 (trajectory set)，并将起点添加到轨迹集中。
     • 初始化开放列表 (open set)，将起始点添加到该集合。
     • 构建闭集合 (closed set)，表示不同时间步长中的节点，防止重复访问。

2. 搜索过程

   • 算法会循环执行，直到开放列表为空或者找到目标位置的轨迹。
   • 每次循环中，算法首先计算开放列表中每个节点的代价 (Cost)，这个代价是基于某些准则（如距离目标点的距离、障碍物距离、安全性等）来估算的。

3. 选择最优节点进行扩展

   • 从开放列表中选择代价最低的节点作为当前节点 (current) 进行扩展，这个节点对应当前车辆的状态 (s_i)。
   • 将当前状态 (s_i) 添加到轨迹集中 (trajectory set)。

4. 检查是否到达目标

   • 如果当前节点就是目标节点，那么规划成功，算法结束，输出轨迹。
   • 否则，继续扩展当前节点。

5. 节点扩展和邻居生成

   • 移除当前节点，并根据时间层在下一层地图中生成邻居节点（邻居节点可能是车辆下一时间步的位置），考虑动态障碍物的变化。
   • 对于每个邻居节点，进行如下操作：
     • 检查该节点是否已经在闭集合中（即是否已经访问过），如果是，则忽略。
     • 如果该节点没有被访问过（即不在开放列表中），则将其加入开放列表，准备在下一步进行代价评估。

6. 时间步进与循环

   • 一旦所有的邻居节点都被扩展完毕，时间 (t) 递增，并继续搜索下一个时间步的状态，重复上述操作直到找到最优轨迹或者开放列表为空。

7. 返回结果

   • 当搜索到达目标位置时，算法会返回已找到的最优轨迹。
   • 如果在开放列表为空时仍未找到路径，则表示搜索失败，可能没有可行的路径。

2.6.2 时空代价复用

在时空联合规划中，由于需要在三维时空空间（包括位置和时间维度）内进行搜索，计算代价往往会消耗较多的计算资源。为了降低搜索耗时，可以通过 时空代价复用 来优化代价计算。时空代价复用的关键在于减少对重复计算的需求，以下是常用的几种优化思路：

1. 缓存与代价复用

   • 缓存计算过的代价：对于已经计算过的时空节点，存储它们的代价。在后续的搜索过程中，如果访问到同一个节点或其状态变化较小的邻居节点，可以直接复用之前计算的代价，而不需要重新计算。
   • 邻近节点的代价估算：由于相邻时间步的节点在空间和时间上通常变化较小，因此可以通过对相邻节点的代价进行微小的调整（例如加上时间或空间步长的权重），而不是从头开始计算代价。这可以大大减少计算量。

2. 启发式估计改进

   • 启发式函数改进：在 Hybrid A* 中，代价函数通常由实际代价和启发式代价两部分组成。启发式函数可以通过更加准确地预测未来的代价来减少不必要的扩展。
     • 预计算距离表：可以预先离线计算出固定空间中的某些位置对之间的最优代价，并将这些结果存储起来，作为启发式函数的一部分。在在线搜索时直接使用这些结果，而不是实时计算距离或代价。
     • 动态调整启发式权重：根据当前障碍物的动态信息，实时调整启发式估计中的权重，进一步提高搜索效率。

3. 稀疏时间层扩展

   • 减少时间层的数量：在时空搜索中，不是每个时间步都必须精确扩展。如果障碍物的动态变化较慢，可以通过跳过中间的时间步来简化计算。即每隔几个时间步（比如 2 或 3 个时间单位）再进行节点扩展，降低搜索规模。
   • 动态时间步长调整：对于动态障碍物较少或移动较慢的区域，可以适当增大时间步长，从而减少每一层时间节点的计算量。在障碍物密集或动态变化较快的区域，可以缩小时间步长，保证路径的精确性。

4. 动态规划思想的引入

   • 共享状态的累积代价复用：可以借鉴动态规划（Dynamic Programming，DP）的思想，将计算过的状态代价储存起来，并在相同状态出现时复用之前的结果。特别是在有多个路径可以到达同一位置状态的情况下，可以复用之前计算过的最优代价，避免重复计算。
   • 增量式规划：对于大多数情况下，障碍物的动态变化是渐进的（而不是突发性的）。因此可以在每次障碍物状态更新时，基于先前规划好的路径进行增量式的规划，而不需要完全重新计算整个路径。

5. 分层规划

   • 分解时空规划问题：将时空联合规划问题分解为两部分：空间规划和时间调度。先在空间上规划出一条静态路径，再根据动态障碍物的变化，对这条路径进行时间上的调整。这种分层处理方法可以显著减少三维搜索的规模和计算量。
   • 局部规划与全局复用：如果某些动态障碍物影响范围有限，可以只对局部区域进行重新规划，而不必重新计算全局轨迹。局部规划结果可以结合已有的全局规划进行快速调整。

3.基于迭代计算的规划方法

暴力搜索存在的潜在问题：

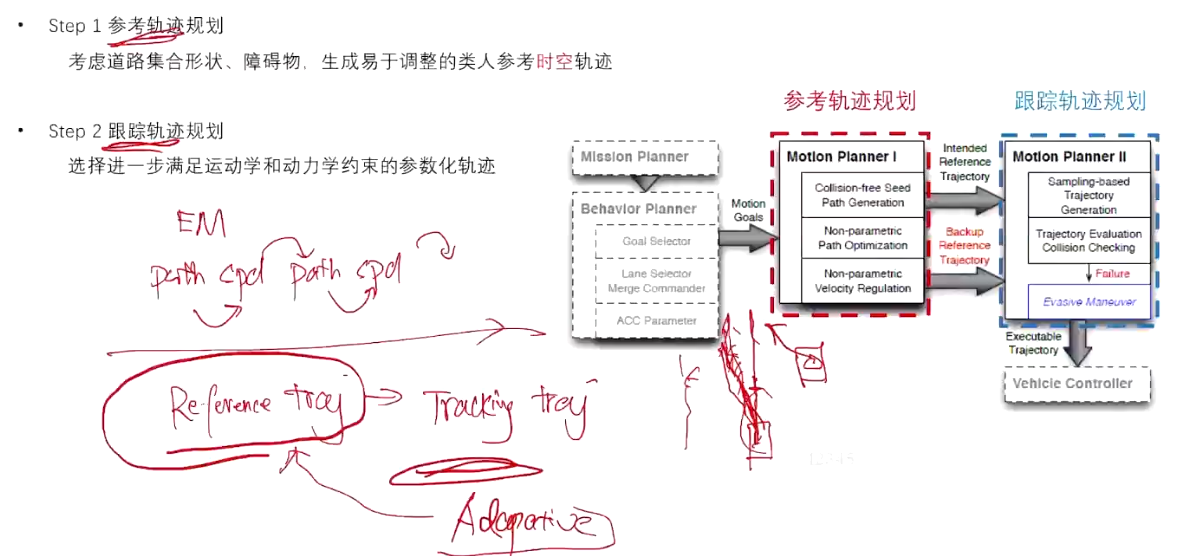
3.1 迭代优化计算方式求解流程

Step 1: 参考轨迹规划

考虑道路集合形状、障碍物，生成易于调整的类人参考时空轨迹。

Step 2: 跟踪轨迹规划

选择进一步满足运动学和动力学约束的参数化轨迹。

参考论文 Focused Trajectory Planning for Autonomous On-Road Driving

3.2 种子路径生成 reference trajectory

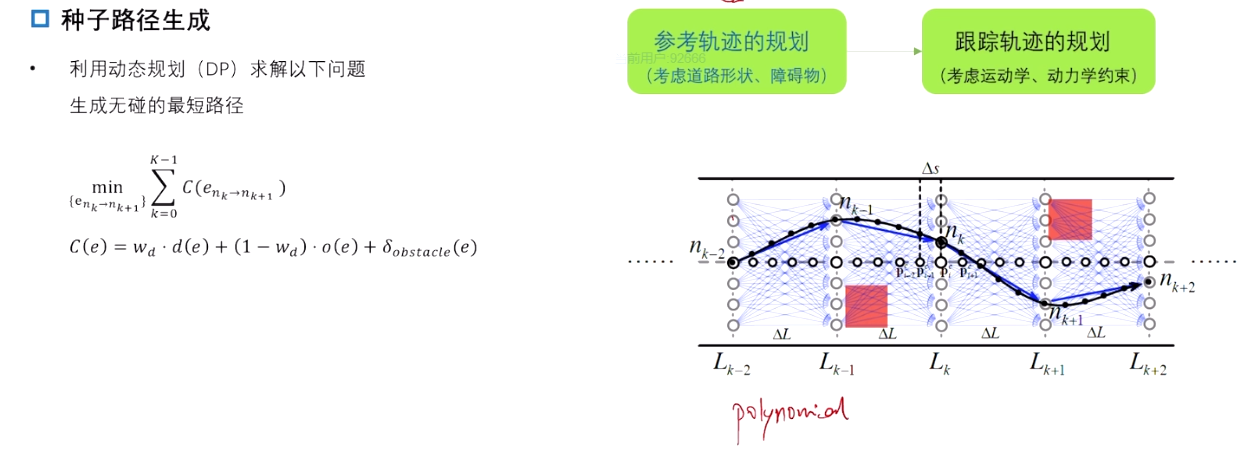
类似lattice 采样，论文中使用直线连接，得到种子路径。

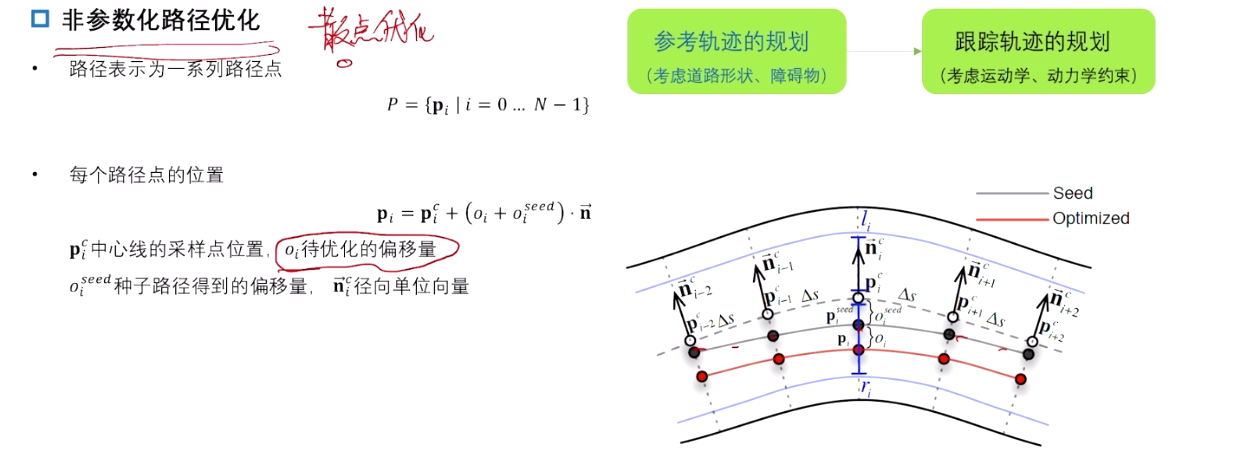
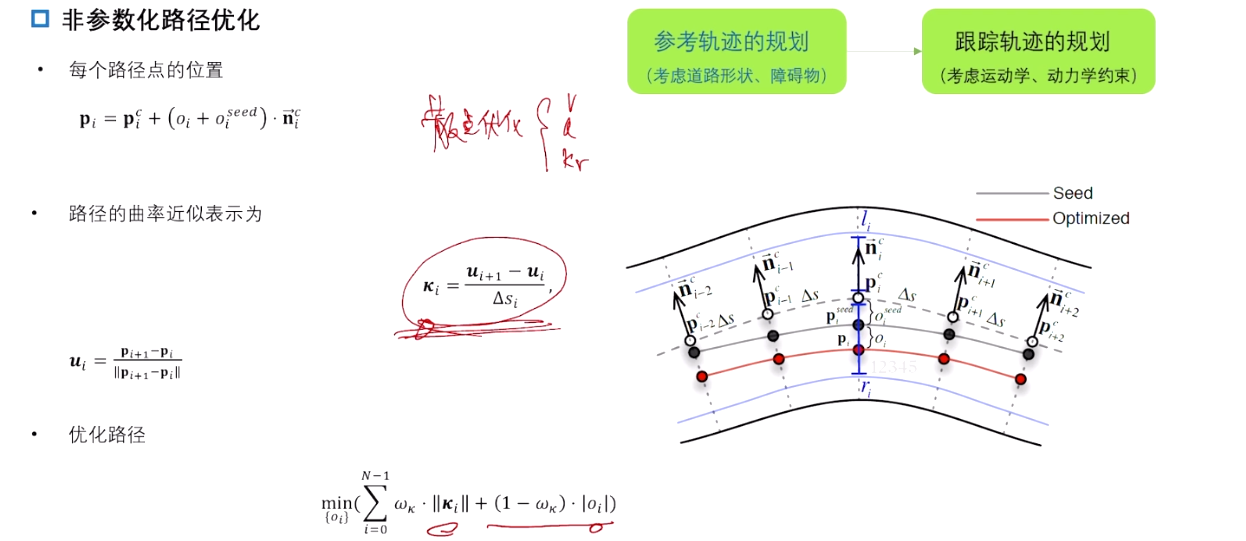
3.3 非参数化路径优化

散点优化：优化每个点的位置。

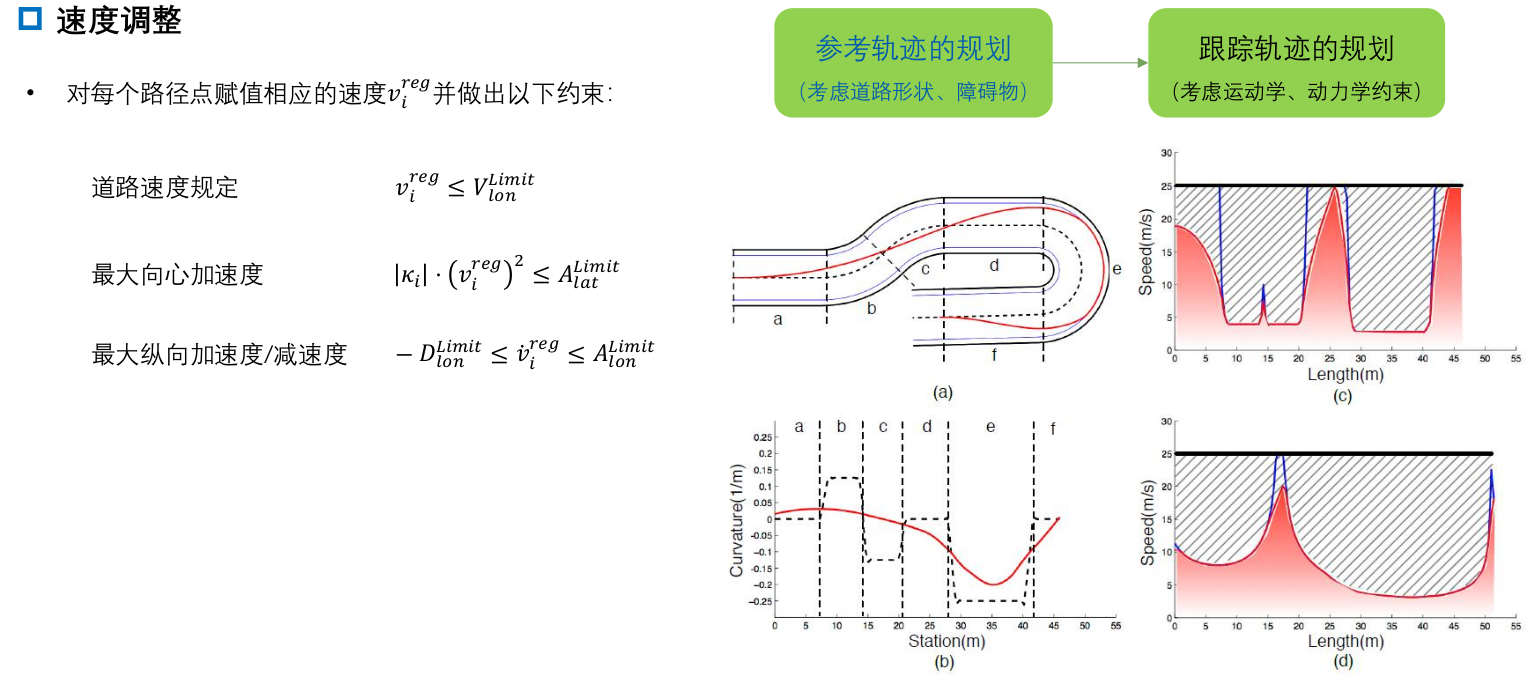
3.4 速度分配

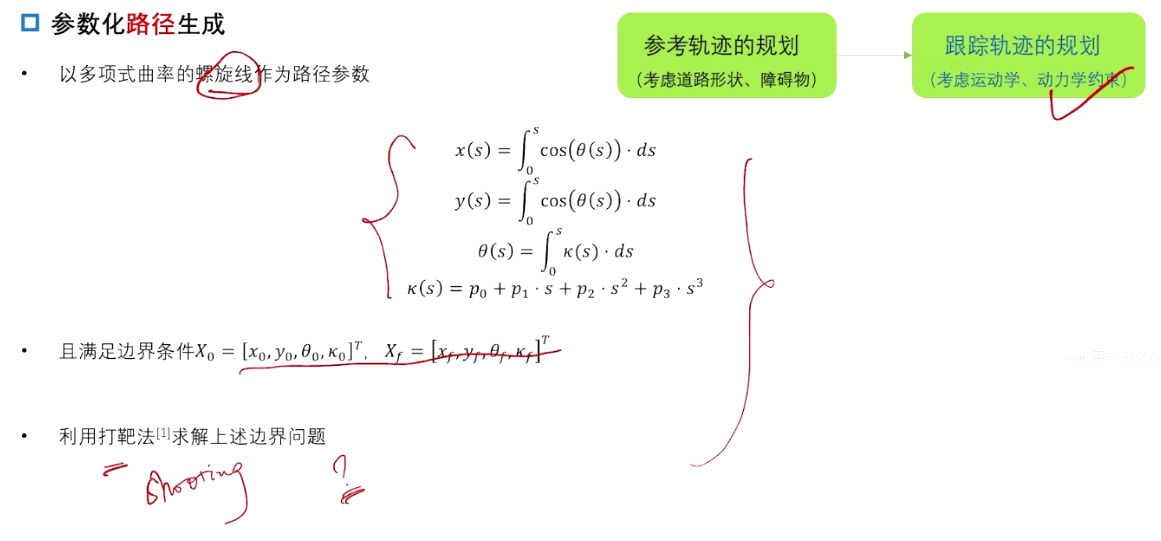
3.5 参数化路径生成

基于散点，拟合出参数化路径。（不一定很有必要，如果上一步的resolution足够细，可以不用这步）

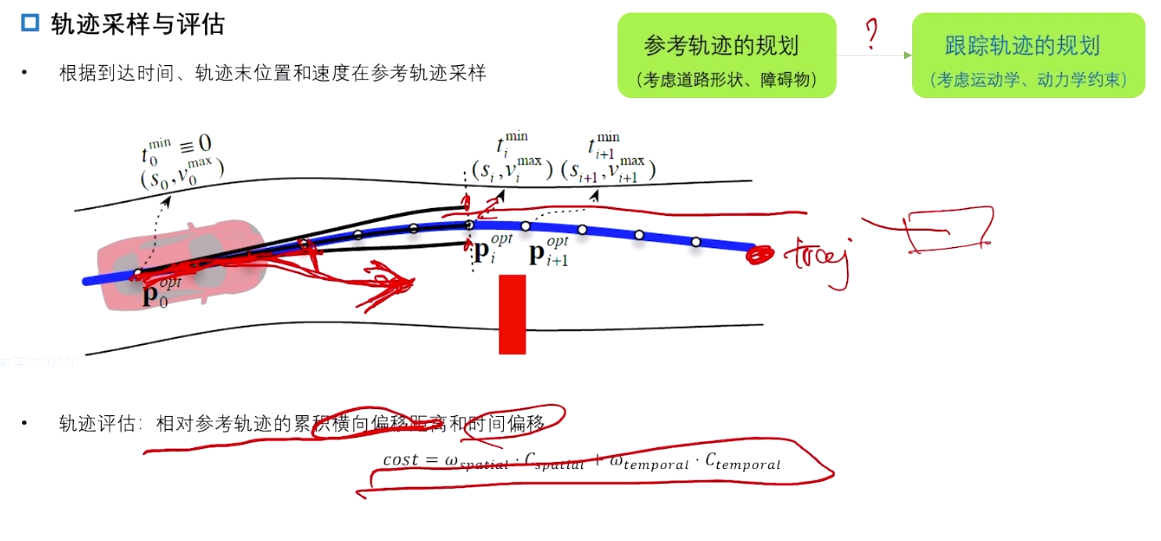
3.6 跟踪轨迹采样与评估

轨迹采样–> 轨迹簇 --> 打分评估。

如果采样的空间越大，对参考轨迹的依赖越弱，越接近于全局路径采样。

采的越少，则越接近参考轨迹。

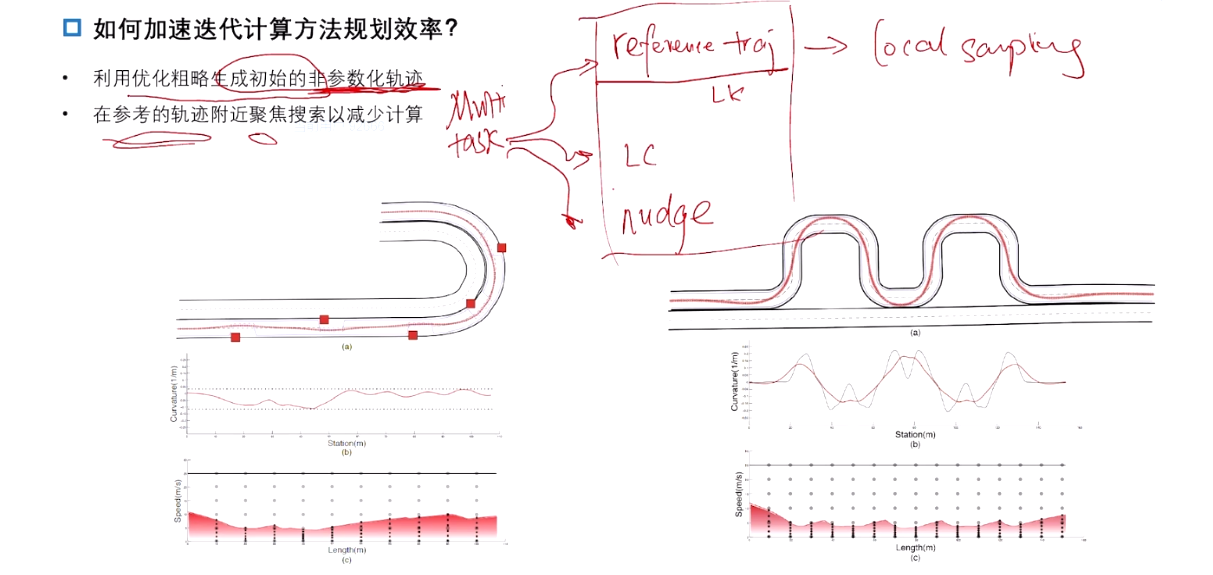
3.7 如何加速迭代计算方法规划效率？

核心：使用轻量化方法生成非参数化轨迹。 multi task： 做多条轨迹，比如line keep、nudge轨迹等。

4.基于时空走廊的时空联合规划方法

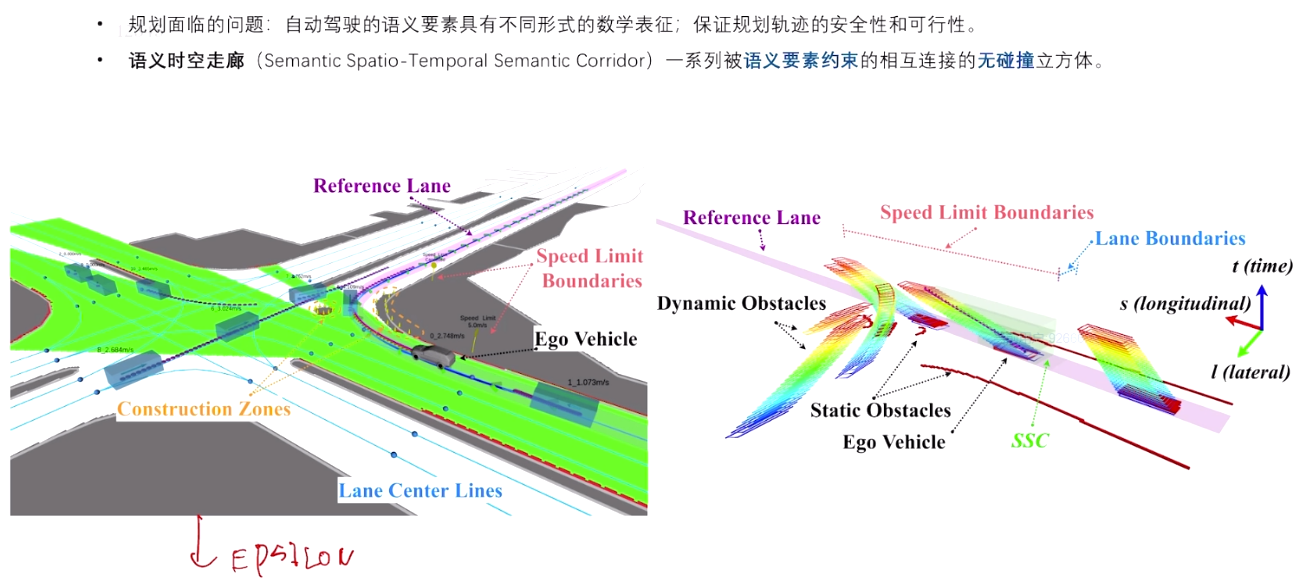
4.1 时空走廊概念

论文链接：EPSILON: An Efficient Planning System for Automated Vehicles in Highly Interactive Environments

4.2 轨迹生成框架

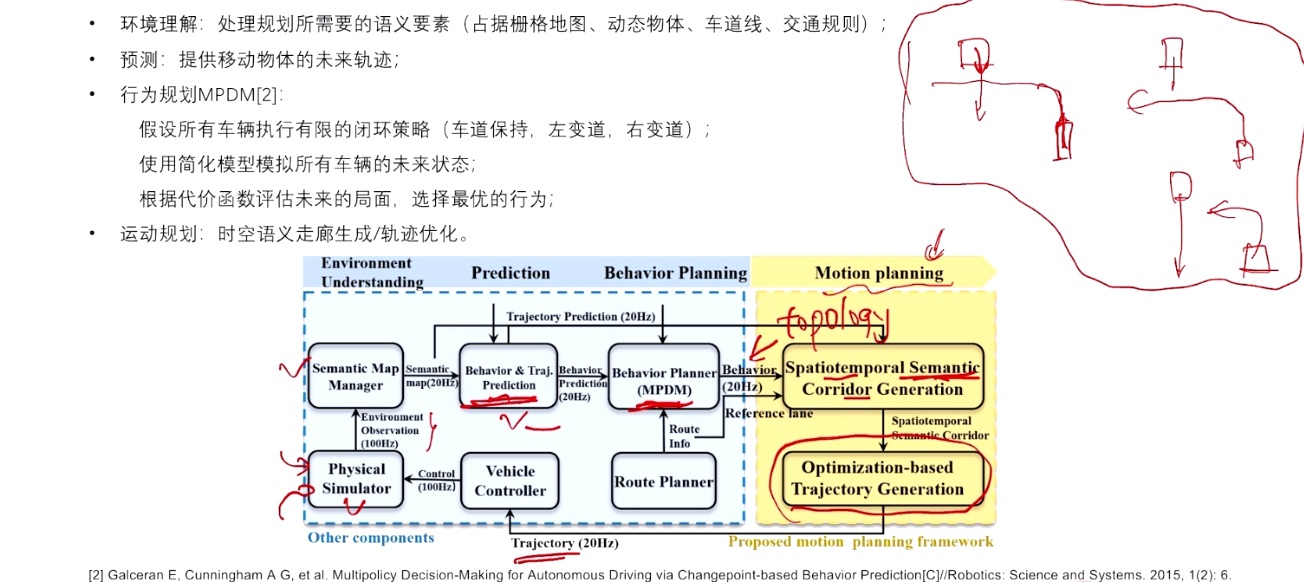
假设一辆自主驾驶汽车正在高速公路上行驶，前方有多辆车和一个即将到来的出口，自车需要在有限的时间内决定是否变道并驶入出口，同时避开周围的车辆。

1: 环境理解

环境理解模块首先从传感器（摄像头、激光雷达等）中获取当前的场景信息，包括：

• 静态环境：道路拓扑、车道线、路标、出口位置等。
• 动态物体：周围车辆的位置、速度、加速度等状态信息。

2: 预测模块

预测模块会基于当前的环境和动态物体的信息，生成每个动态物体的轨迹预测和行为预测：

• 轨迹预测：系统会预测前方车辆未来几秒的可能位置。例如，假设前方车辆将保持当前车道并匀速行驶，预测车辆在未来几秒的位置。
• 行为预测：系统推测前方车辆的意图，比如某辆车可能打算变道，或者另一辆车可能会减速。

3: 行为规划（MPDM）

基于预测信息，行为规划模块生成多个可选的策略。比如：

• 策略 1：继续保持当前车道，并在出口前方通过减速避开前车。
• 策略 2：加速变道到右侧车道，直接驶入出口。

每个策略都会生成一条对应的预期轨迹和行为方案，计算系统根据代价函数选择最优策略，比如考虑安全性、时间、能耗等因素。

4: 时空联合轨迹生成

一旦选择了最佳行为，进入时空轨迹生成过程：

• 时空走廊生成：根据目标车道或路线，系统在三维时空图中划定一个走廊，确保车辆未来的运动限制在这个区域内，避免碰撞。
• 优化轨迹生成：在时空走廊中，系统利用优化算法（如梯度下降或QP）生成车辆的最优轨迹，考虑到平滑性、速度限制、加速度约束等。
  • 路径：生成车辆的空间轨迹，确保它在物理上保持安全距离并满足道路约束。
  • 速度：在空间路径的基础上，进一步优化速度曲线，确保车辆平稳地加速或减速，避免急刹或超速。

5: 轨迹跟踪与执行

最终生成的轨迹将作为输入传递给控制模块，控制模块根据轨迹调节车辆的方向、速度、加速等行为。

4.3 时空走廊生成

4.3.1 语义时空走廊的障碍物要素

核心思想：任何一个语义都可以抽象为时空下的约束或cost，并绑定到convex space 上, 转为QP问题。

比如 红灯：某个时间时，不能超过某个S。动态障碍物：某个时空下，不能碰到它的S、L。 变道：经过某个l时,总的时间要被限制，并且无碰撞。

4.3.2 语义时空走廊的约束要素

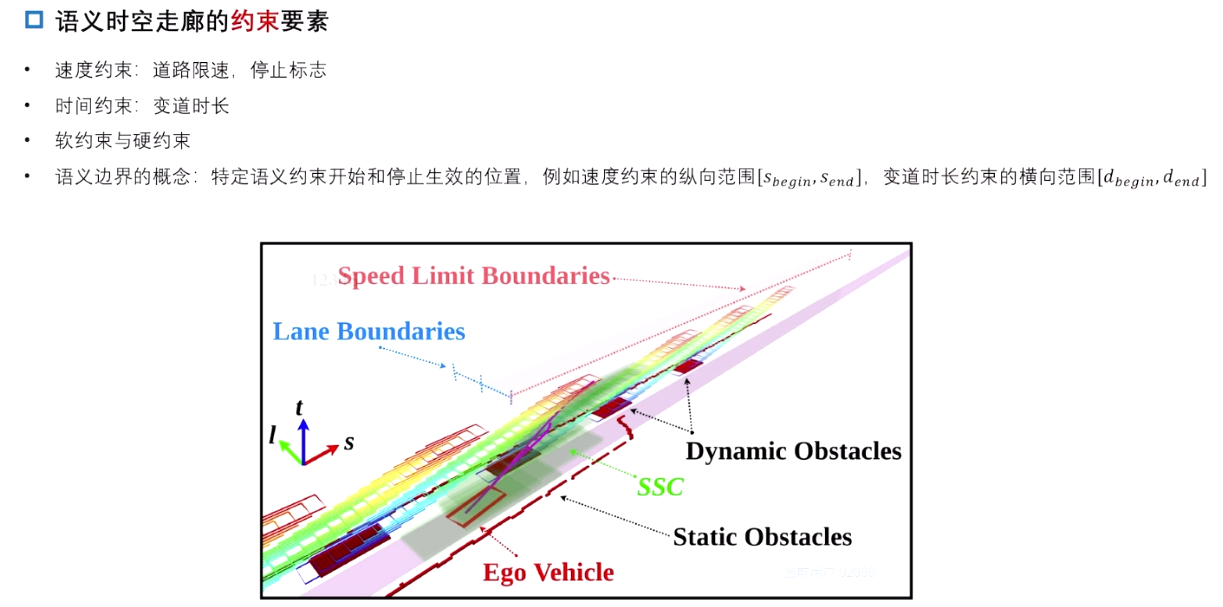
4.3.3 语义时空走廊构建 ：输入数据

他车状态：从一个初始解出发，由MPDM得到，他车行为及轨迹的粗解；

静动态障碍物：通过时空走廊抽象出来；

语义边界：红绿灯、道路边界、变道时长、道路限速等；

根据初始解与约束条件，如何求解？

4.3.4 语义时空走廊构建：生成种子

4.3.5 语义时空走廊构建：膨胀立方体

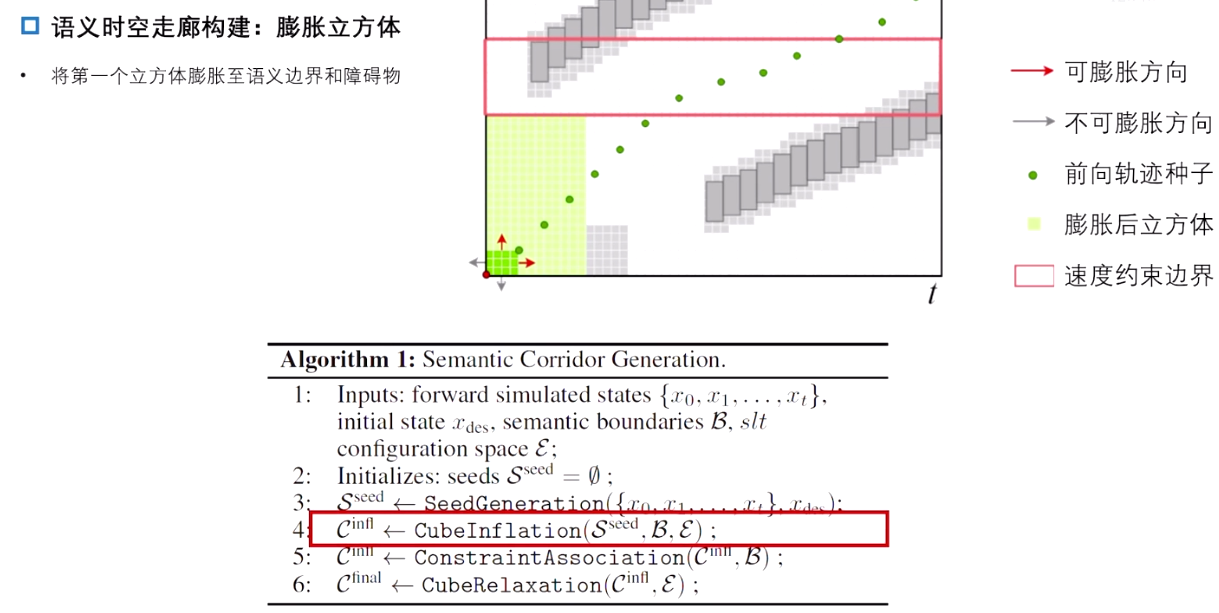
• 初始生成的种子点已经避开了障碍物，但它们只是代表车辆能够行驶的初始路径。膨胀操作会根据障碍物的分布和车辆可能的未来状态，将初始路径扩展为一个安全走廊，使得车辆可以在一定的范围内自由调整，以应对动态变化。

4.3.6 语义时空走廊构建：关联约束

• 关联约束的作用
  关联约束（Constraint Association）包括了语义约束（例如交通规则、车道线约束）和速度约束等。在膨胀种子点并生成初步的时空走廊后，关联约束被引入来进一步减少路径选择的自由度。这些约束会收缩时空走廊的解空间，限制车辆行驶时的合法范围。

• 衔接处问题：在不同的膨胀区域之间，关联约束需要确保两个区域能够平滑且可行地连接。如果衔接处处理不当，可能会导致路径不连续或存在过于急促的转折，影响车辆行驶的安全和稳定性。

• 在两个膨胀区域的衔接处，系统需要选择靠近的种子点来实现衔接。通过对相邻种子点的合理选择，衔接处可以保持平滑的过渡，避免突兀的转弯或急剧的速度变化。

• 由于关联约束的引入，特别是在衔接处，解空间会进一步收缩。这意味着车辆在该区域的可行运动范围被限制在更小的空间内，从而减少了可能的路径选择。

• 解空间的减少可以有效过滤掉不符合交通规则或动力学约束的路径，但同时也可能降低路径的灵活性，使得系统需要更加精细地处理衔接处的问题，确保生成的路径在有限的解空间内仍然保持最优。

4.3.7 语义时空走廊构建：放宽边界

• 初步生成时空走廊时，由于硬约束（如障碍物、车道线）和关联约束的作用，解空间可能会变得过于狭窄，导致规划的路径不够灵活，或者无法找到可行解。为了增加系统的灵活性，可以进行边界放宽操作
• 放宽边界的操作通过引入软约束，扩大了时空走廊的解空间，增加了轨迹规划的灵活性。虽然一些软约束可以在代价权衡下被适度违反，但硬约束（如避障和物理约束）始终严格保持不变，从而确保生成的路径在实际应用中是安全和可行的。

4.3.8 其他问题

1. 表达形式是否一定要是矩形，cube 形状？

2. 对语义的遵从程度，与空间的自由度如何平衡？

3. 基于走廊，如何生成轨迹。trajectory generation？

4.4 优化轨迹生成

4.4.1 保证安全性和可行性的轨迹生成

采用参数优化的方法，基底选用贝塞尔曲线。通过优化控制点，决定曲线的表达形式。

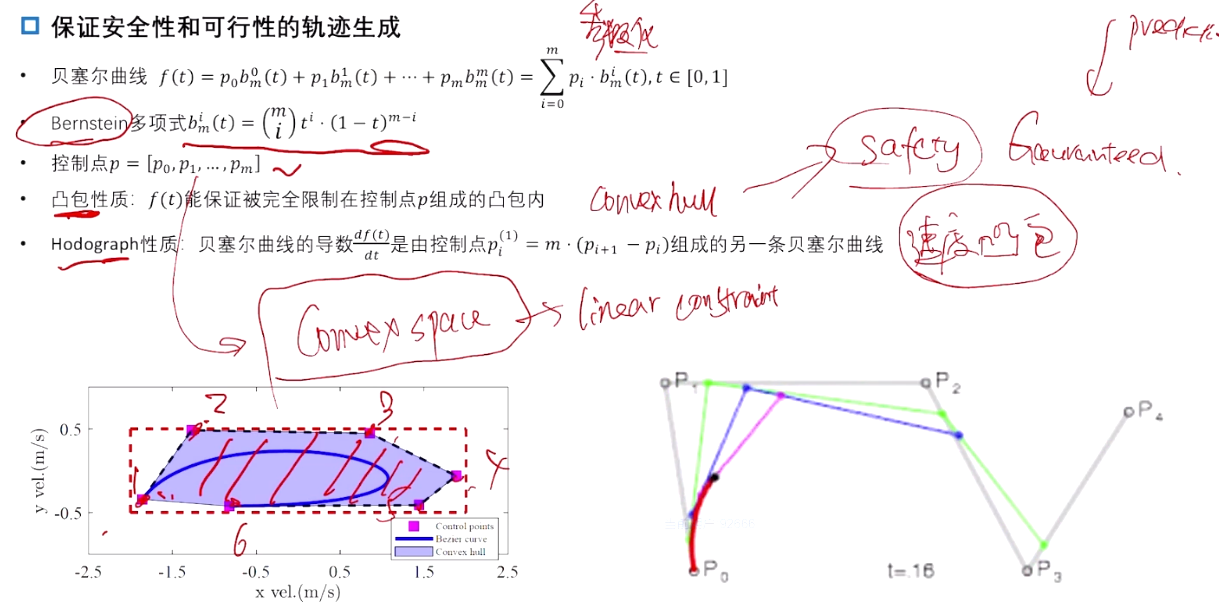
定义：
贝塞尔曲线是一条由若干控制点决定的平滑曲线。控制点并不一定在曲线上，但它们的排列方式影响曲线的形状。

• 一条n阶贝塞尔曲线由 $n+1$ 个控制点 $(P_0,P_1,...,P_n)$ 构成。曲线是这些控制点的加权平均，随着参数 $(t)$ 从0到1逐步变化。
• 参数方程为：
  $$B(t)=\sum _{i=0}^n\left(\genfrac{}{}{0ex}{}{n}{i}\right)(1-t{)}^{n-i}{t}^i{P}_i$$
  其中，$(t)$ 是从 0 到 1 的参数，$((\genfrac{}{}{0ex}{}{n}{i}))$是二项式系数。

特性：

• 起点与终点：贝塞尔曲线的起点和终点分别是第一个和最后一个控制点 (P_0) 和 (P_n)。

• 形状控制：中间的控制点 (P_1, …, P_{n-1}) 决定了曲线的形状。曲线不会严格经过这些点，但它的整体走向和曲率受它们的影响。

• 凸包性：曲线可以完全被限制在控制点组成的凸包内。 将控制点约束在convex space 内，则可保证生成的轨迹绝对安全。 --> 位置凸包。

• Hodograph 性质： 曲线的导数也是贝塞尔曲线，由控制点决定，可将速度约束在一个合理的范围。–> 速度凸包。

贝塞尔曲线的两个重要特性——凸包性和Hodograph 性质，这两个特性在路径规划与轨迹生成中尤为重要，尤其在保证安全性和控制速度的过程中起到了关键作用。

1. 凸包性（Convex Hull Property）：
   贝塞尔曲线的凸包性意味着曲线将始终被限制在其控制点所组成的凸包内。

   • 定义：对于一条贝塞尔曲线，它的所有点都位于其控制点构成的凸包（convex hull）中。凸包是由控制点围成的一个最小的凸多边形或凸多面体，曲线不会超出这个范围。

   • 轨迹生成的安全性：

     • 在路径规划中，通过约束控制点的位置，可以保证生成的贝塞尔曲线不会穿越危险区域（如障碍物）。
     • 具体来说，若控制点被约束在安全区域的凸空间内（如在没有障碍物的路面上），则根据凸包性，贝塞尔曲线的轨迹必然不会超出该安全区域。这一特性使得贝塞尔曲线成为生成绝对安全轨迹的有效工具。

2. Hodograph 性质（Hodograph Property）：
   贝塞尔曲线的Hodograph性质与其导数的表现有关，意味着贝塞尔曲线的导数（即速度向量）也是一条贝塞尔曲线，并由控制点决定。

   • 定义：贝塞尔曲线的导数（速度曲线）仍然是一条贝塞尔曲线，其控制点是原曲线控制点的差分。因此，通过控制贝塞尔曲线的控制点，不仅可以控制位置，还可以控制曲线的导数（速度）。
   • 速度约束与控制：
     • 通过调节控制点之间的间距和位置，能够控制贝塞尔曲线的导数变化，从而约束速度变化。
     • 贝塞尔曲线的Hodograph性质意味着速度曲线也被限制在控制点形成的凸包中。通过约束控制点的位置，可以确保生成的曲线在满足某种速度要求的范围内。

• 位置凸包：贝塞尔曲线的凸包性保证了路径在控制点构成的凸空间内。通过将控制点约束在安全的凸区域内，可以确保生成的轨迹在物理空间上是安全的，不会撞上障碍物。
• 速度凸包：贝塞尔曲线的Hodograph性质保证了速度的变化也受到控制点的约束。通过精确控制控制点，可以将速度变化约束在合理的范围内，确保车辆的加速和减速都在安全范围内。

4.4.2 轨迹表示

对于每段轨迹，约束每个控制点，使其在对应的凸包内。

4.4.3 轨迹优化问题

构造优化问题：最小化 jerk，转为 QP 问题，求解轨迹。

4.4.4 EPSILON 代码

EPSILON 开源代码参考地址

SscPlanner::RunOnce()

EPSILON/util/ssc_planner/src/ssc_planner/ssc_planner.cc

它的主要功能是进行单次轨迹规划操作，包含了几个关键步骤，如获取车辆状态、处理地图数据、构建时空走廊、优化轨迹等。

1. 时间戳与车辆状态获取

   stamp_ = map_itf_->GetTimeStamp();
   if (map_itf_->GetEgoVehicle(&ego_vehicle_) != kSuccess) {
     LOG(ERROR) << "[Ssc]fail to get ego vehicle info.";
     return kWrongStatus;
   }
   

• 获取当前的时间戳（stamp_），并通过接口 map_itf_ 获取车辆的自车信息（ego_vehicle_）。如果获取失败，函数返回错误状态 kWrongStatus。

2. 初始化与状态变换

   if (!has_initial_state_) {
     initial_state_ = ego_vehicle_.state();
   }
   has_initial_state_ = false;
   
   is_lateral_independent_ = initial_state_.velocity > cfg_.planner_cfg().low_speed_threshold() ? true : false;
   

• 如果尚未设置初始状态，则使用当前车辆状态（ego_vehicle_.state()）作为初始状态，并将 has_initial_state_ 置为 false。
• 根据车辆速度判断横向是否独立，当速度低于某一阈值时，横向独立性为 false。

3. 参考路径与坐标变换

   if (map_itf_->GetLocalReferenceLane(&nav_lane_local_) != kSuccess) {
     LOG(ERROR) << "[Ssc]fail to find ego lane.";
     return kWrongStatus;
   }
   stf_ = common::StateTransformer(nav_lane_local_);
   

• 获取自车的局部参考车道（nav_lane_local_），并创建一个状态转换器（stf_），用于将车辆状态从全局坐标系变换到 Frenet 坐标系。

4. 坐标系转换与障碍物信息获取

   if (stf_.GetFrenetStateFromState(initial_state_, &initial_frenet_state_) != kSuccess) {
     LOG(ERROR) << "[Ssc]fail to get init state frenet state.";
     return kWrongStatus;
   }
   

• 通过 stf_ 将车辆的初始状态（全局坐标）转换到 Frenet 坐标系，并存储在 initial_frenet_state_ 中。如果转换失败，返回错误状态。
• 接着从地图接口中获取障碍物地图和栅格信息，这些信息后续用于避障规划。

5. 自车前向轨迹

   if (map_itf_->GetForwardTrajectories(&forward_behaviors_, &forward_trajs_, &surround_forward_trajs_) != kSuccess) {
     LOG(ERROR) << "[Ssc]fail to get forward trajectories.";
     return kWrongStatus;
   }
   

• 获取车辆的前向轨迹和前向行为，供后续使用。

6. 时空地图构建与轨迹生成

   p_ssc_map_->ResetSscMap(initial_frenet_state_);
   for (int i = 0; i < num_behaviors; ++i) {
     if (!cfg_.planner_cfg().is_fitting_only()) {
       if (p_ssc_map_->ConstructSscMap(surround_forward_trajs_fs_[i], obstacle_grids_fs_)) {
         LOG(ERROR) << "[Ssc]fail to construct ssc map.";
         return kWrongStatus;
       }
     }
   
     if (p_ssc_map_->ConstructCorridorUsingInitialTrajectory(p_ssc_map_->p_3d_grid(), forward_trajs_fs_[i]) != kSuccess) {
       LOG(ERROR) << "[Ssc]fail to construct corridor for behavior " << i;
       return kWrongStatus;
     }
   }
   

• 重置时空地图，并通过周围车辆的轨迹和障碍物信息构建一个时空走廊（corridor）。时空走廊是在轨迹生成中考虑时空上的可行空间。
• 每个行为对应的轨迹在时空网格上生成一个安全走廊。如果生成失败，返回错误状态。

7. 轨迹优化

   if (RunQpOptimization() != kSuccess) {
     LOG(ERROR) << "[Ssc]fail to optimize qp trajectories.";
     return kWrongStatus;
   }
   

• 调用 RunQpOptimization() 进行轨迹的二次规划优化，确保最终轨迹平滑、安全并符合约束条件。如果优化失败，函数返回错误。

8. 更新当前行为的轨迹

   if (UpdateTrajectoryWithCurrentBehavior() != kSuccess) {
     LOG(ERROR) << "[Ssc]fail: current behavior " << static_cast<int>(ego_behavior_) << " not valid.";
     return kWrongStatus;
   }
   

SscMap::ConstructCorridorUsingInitialTrajectory()

EPSILON/util/ssc_planner/src/ssc_planner/ssc_map.cc

根据初始的车辆轨迹来构建时空走廊，用于后续的路径规划。具体来说，这个过程分为两个阶段：种子点生成和立方体膨胀。

1. 第一阶段：获取种子点

vec_E<Vec3i> traj_seeds;
int num_states = static_cast<int>(trajs.size());
if (num_states > 1) {
    bool first_seed_determined = false;
    for (int k = 0; k < num_states; ++k) {
        std::array<decimal_t, 3> p_w = {};
        if (!first_seed_determined) {
            // 初始状态的s、d、t值
            decimal_t s_0 = initial_fs_.vec_s[0];
            decimal_t d_0 = initial_fs_.vec_dt[0];
            decimal_t t_0 = initial_fs_.time_stamp;
            std::array<decimal_t, 3> p_w_0 = {s_0, d_0, t_0};
            auto coord_0 = p_grid->GetCoordUsingGlobalPosition(p_w_0);

            // 轨迹的第k个点的s、d、t值
            decimal_t s_1 = trajs[k].frenet_state.vec_s[0];
            decimal_t d_1 = trajs[k].frenet_state.vec_dt[0];
            decimal_t t_1 = trajs[k].frenet_state.time_stamp;
            std::array<decimal_t, 3> p_w_1 = {s_1, d_1, t_1};
            auto coord_1 = p_grid->GetCoordUsingGlobalPosition(p_w_1);

            // 检查点是否在地图范围内
            if (!p_grid->CheckCoordInRange(coord_1)) {
                continue;
            }

            // 确定第一个有效种子点，并将其加入种子列表
            first_seed_determined = true;
            traj_seeds.push_back(Vec3i(coord_0[0], coord_0[1], coord_0[2]));
            traj_seeds.push_back(Vec3i(coord_1[0], coord_1[1], coord_1[2]));
        } else {
            decimal_t s = trajs[k].frenet_state.vec_s[0];
            decimal_t d = trajs[k].frenet_state.vec_dt[0];
            decimal_t t = trajs[k].frenet_state.time_stamp;
            p_w = {s, d, t};
            auto coord = p_grid->GetCoordUsingGlobalPosition(p_w);

            if (!p_grid->CheckCoordInRange(coord)) {
                continue;
            }

            traj_seeds.push_back(Vec3i(coord[0], coord[1], coord[2]));
        }
    }
}

• traj_seeds 是生成的种子点列表，用来构建走廊。
• 每个轨迹点的 s, d, t 值通过 Frenet 坐标系表示，并被转换为地图中的坐标系，通过 p_grid->GetCoordUsingGlobalPosition 获取坐标索引。
• 起始时，代码会检查每个轨迹点是否在地图的范围内并过滤掉无效点。如果通过检查，第一个有效点被确定为种子点，后续点根据轨迹依次加入。

2. 第二阶段：膨胀立方体

common::DrivingCorridor driving_corridor;
bool is_valid = true;
auto seed_num = static_cast<int>(traj_seeds.size());
if (seed_num < 2) {
    driving_corridor.is_valid = false;
    driving_corridor_vec_.push_back(driving_corridor);
    is_valid = false;
    return kWrongStatus;
}

for (int i = 0; i < seed_num; ++i) {
    if (i == 0) {
        common::AxisAlignedCubeNd<int, 3> cube;
        GetInitialCubeUsingSeed(traj_seeds[i], traj_seeds[i + 1], &cube);
        if (!CheckIfCubeIsFree(p_grid, cube)) {
            LOG(ERROR) << "[Ssc] SccMap - Initial cube is not free, seed id: " << i;

            common::DrivingCube driving_cube;
            driving_cube.cube = cube;
            driving_cube.seeds.push_back(traj_seeds[i]);
            driving_cube.seeds.push_back(traj_seeds[i + 1]);
            driving_corridor.cubes.push_back(driving_cube);

            driving_corridor.is_valid = false;
            driving_corridor_vec_.push_back(driving_corridor);
            is_valid = false;
            break;
        }

        // 膨胀立方体
        std::array<bool, 6> dirs_disabled = {false, false, false, false, false, false};
        InflateCubeIn3dGrid(p_grid, dirs_disabled, config_.inflate_steps, &cube);

        common::DrivingCube driving_cube;
        driving_cube.cube = cube;
        driving_cube.seeds.push_back(traj_seeds[i]);
        driving_corridor.cubes.push_back(driving_cube);
    } else {
        if (CheckIfCubeContainsSeed(driving_corridor.cubes.back().cube, traj_seeds[i])) {
            driving_corridor.cubes.back().seeds.push_back(traj_seeds[i]);
            continue;
        } else {
            Vec3i seed_r = driving_corridor.cubes.back().seeds.back();
            driving_corridor.cubes.back().seeds.pop_back();
            driving_corridor.cubes.back().cube.upper_bound[2] = seed_r(2);
            i = i - 1;

            common::AxisAlignedCubeNd<int, 3> cube;
            GetInitialCubeUsingSeed(traj_seeds[i], traj_seeds[i + 1], &cube);

            if (!CheckIfCubeIsFree(p_grid, cube)) {
                LOG(ERROR) << "[Ssc] SccMap - Initial cube is not free, seed id: " << i;
                common::DrivingCube driving_cube;
                driving_cube.cube = cube;
                driving_cube.seeds.push_back(traj_seeds[i]);
                driving_cube.seeds.push_back(traj_seeds[i + 1]);
                driving_corridor.cubes.push_back(driving_cube);

                driving_corridor.is_valid = false;
                driving_corridor_vec_.push_back(driving_corridor);
                is_valid = false;
                break;
            }

            InflateCubeIn3dGrid(p_grid, dirs_disabled, config_.inflate_steps, &cube);
            common::DrivingCube driving_cube;
            driving_cube.cube = cube;
            driving_cube.seeds.push_back(traj_seeds[i]);
            driving_corridor.cubes.push_back(driving_cube);
        }
    }
}

if (is_valid) {
    driving_corridor.cubes.back().cube.upper_bound[2] = traj_seeds.back()(2);
    driving_corridor.is_valid = true;
    driving_corridor_vec_.push_back(driving_corridor);
}

• 使用种子点来初始化立方体（即时空走廊的基础单元），通过GetInitialCubeUsingSeed函数根据种子点创建立方体。
• CheckIfCubeIsFree检查立方体内是否存在障碍物，确保立方体是可行区域。如果立方体被障碍物占据，则该走廊被标记为无效。
• InflateCubeIn3dGrid通过在 3D 网格中膨胀立方体，来扩大走廊的安全范围，使得车辆在更宽的区域内可以行驶。
• 最终，所有膨胀后的立方体构成了一个时空走廊。

1. 种子点生成：根据车辆的初始轨迹，将轨迹点映射到网格地图中，生成对应的种子点列表。
2. 立方体膨胀：使用这些种子点生成初始立方体，并通过膨胀来构建每个行为对应的时空走廊。
3. 可行性检查：如果某个立方体无法通过障碍物检查，该时空走廊被标记为无效。

最终的输出是一个包含多个膨胀立方体的走廊，每个立方体表示一个在时空中可行的区域。

SscPlanner::RunQpOptimization()

EPSILON/util/ssc_planner/src/ssc_planner/ssc_planner.cc

在时空走廊的约束条件下，使用贝塞尔曲线进行轨迹优化。

1. 获取时空走廊和有效性判断

   vec_E<vec_E<common::SpatioTemporalSemanticCubeNd<2>>> cube_list = p_ssc_map_->final_corridor_vec();
   std::vector<int> if_corridor_valid = p_ssc_map_->if_corridor_valid();
   

• cube_list 是存储时空走廊数据的列表，每个走廊对应一个行为。
• if_corridor_valid 用于记录每个走廊是否有效。如果没有有效的走廊，代码会记录错误并返回。

2. 检查走廊数量与行为的一致性

   if (cube_list.size() != forward_behaviors_.size()) {
     LOG(ERROR) << "[Ssc]cube list " << static_cast<int>(cube_list.size())
                << " not consist with behavior size: "
                << static_cast<int>(forward_behaviors_.size());
     return kWrongStatus;
   }
   

• 代码确保走廊数量和前向行为的数量是一致的。如果不一致，则记录错误并返回错误状态。

3. 轨迹、行为、走廊的初始化

   qp_trajs_.clear();
   primitive_trajs_.clear();
   valid_behaviors_.clear();
   corridors_.clear();
   ref_states_list_.clear();
   

• 初始化多个容器，清空之前的轨迹、走廊、行为等数据，为接下来的优化过程做准备。

4. 遍历每个时空走廊和行为

   for (int i = 0; i < static_cast<int>(cube_list.size()); i++) {
     if (if_corridor_valid[i] == 0) {
       LOG(ERROR) << "[Ssc]fail: for behavior "
                  << static_cast<int>(forward_behaviors_[i])
                  << " has no valid corridor.";
       continue;
     }
   

• 遍历 cube_list，即每个行为的时空走廊。
• 如果走廊无效（if_corridor_valid[i] == 0），则跳过该走廊并记录错误。

5. 起点与终点约束

   vec_E<Vecf<2>> start_constraints;
   start_constraints.push_back(Vecf<2>(ego_frenet_state_.vec_s[0], ego_frenet_state_.vec_dt[0]));
   

• 设置轨迹的起点约束，起点通常是自车的状态（ego_frenet_state_）。

• start_constraints 是一个二维向量的集合，表示车辆在 s-d 坐标系下的起点位置、速度等信息。

  vec_E<Vecf<2>> end_constraints;
  end_constraints.push_back(Vecf<2>(fs_vehicle_traj[num_states - 1].frenet_state.vec_s[0], fs_vehicle_traj[num_states - 1].frenet_state.vec_dt[0]));
  

• 设置轨迹的终点约束，终点是前向轨迹的最后一个点。

6. 贝塞尔曲线轨迹优化

   common::SplineGenerator<5, 2> spline_generator;
   BezierSpline bezier_spline;
   
   if (spline_generator.GetBezierSplineUsingCorridor(cube_list[i], start_constraints, end_constraints, ref_stamps, ref_points, cfg_.planner_cfg().weight_proximity(), &bezier_spline) != kSuccess) {
     LOG(ERROR) << "[Ssc]fail: solver error for behavior " << static_cast<int>(forward_behaviors_[i]);
     bezier_spline_gen_success = false;
   }
   

• 这里调用贝塞尔曲线生成器 spline_generator，使用时空走廊、起点、终点和参考轨迹点（ref_points）生成贝塞尔曲线。如果生成失败，记录错误并跳过该行为。

7. 时空走廊的可行性检查

   if (CorridorFeasibilityCheck(cube_list[i]) != kSuccess) {
     LOG(ERROR) << "[Ssc]fail: corridor not valid for optimization.";
     continue;
   }
   

• 在贝塞尔曲线生成前，对走廊进行可行性检查（CorridorFeasibilityCheck）。如果走廊不符合要求，直接跳过优化。

8. 存储优化后的轨迹

   qp_trajs_.push_back(bezier_spline);
   primitive_trajs_.push_back(primitive);
   corridors_.push_back(cube_list[i]);
   ref_states_list_.push_back(ref_states);
   valid_behaviors_.push_back(forward_behaviors_[i]);
   

• 将优化后的贝塞尔轨迹 bezier_spline、初级轨迹 primitive 以及对应的时空走廊和行为存储起来，供后续使用。

5. 参考链接

《自动驾驶预测与决策技术》
EPSILON 开源代码参考地址
Focused Trajectory Planning for Autonomous On-Road Driving
EPSILON: An Efficient Planning System for Automated Vehicles in Highly Interactive Environments

Part1_自动驾驶决策规划简介
Part2_基于模型的预测方法
Part3_路径与轨迹规划