【LetMeFly】2374.边积分最高的节点：模拟

力扣题目链接：https://leetcode.cn/problems/node-with-highest-edge-score/

给你一个有向图，图中有 n 个节点，节点编号从 0 到 n - 1 ，其中每个节点都 恰有一条 出边。

图由一个下标从 0 开始、长度为 n 的整数数组 edges 表示，其中 edges[i] 表示存在一条从节点 i 到节点 edges[i] 的 有向 边。

节点 i 的 边积分 定义为：所有存在一条指向节点 i 的边的节点的 编号 总和。

返回 边积分 最高的节点。如果多个节点的 边积分 相同，返回编号 最小 的那个。

 

示例 1：

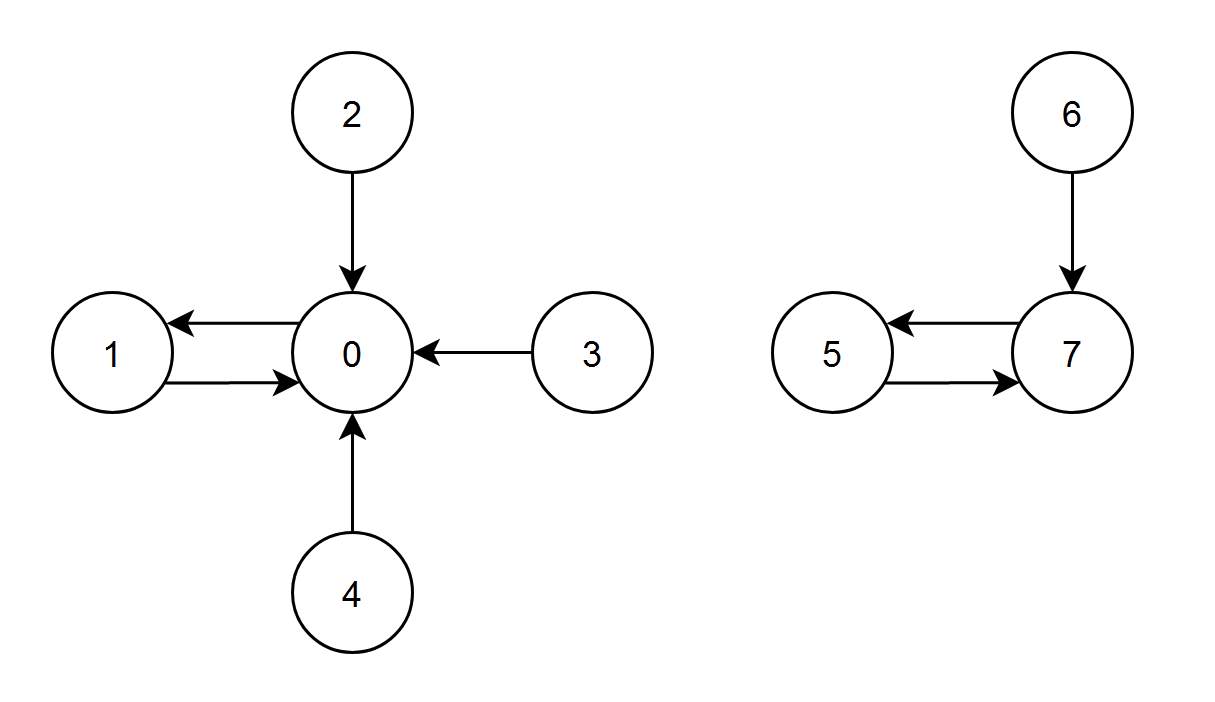
输入：edges = [1,0,0,0,0,7,7,5]
输出：7
解释：
- 节点 1、2、3 和 4 都有指向节点 0 的边，节点 0 的边积分等于 1 + 2 + 3 + 4 = 10 。
- 节点 0 有一条指向节点 1 的边，节点 1 的边积分等于 0 。
- 节点 7 有一条指向节点 5 的边，节点 5 的边积分等于 7 。
- 节点 5 和 6 都有指向节点 7 的边，节点 7 的边积分等于 5 + 6 = 11 。
节点 7 的边积分最高，所以返回 7 。

示例 2：

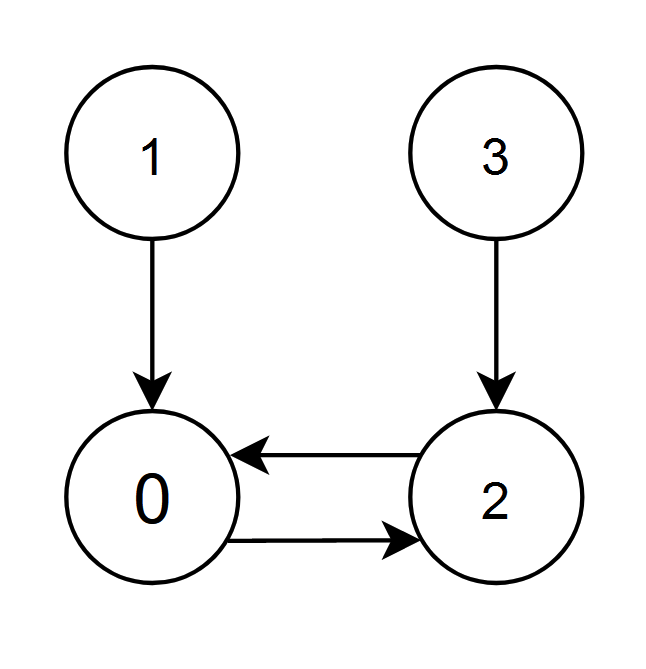
输入：edges = [2,0,0,2]
输出：0
解释：
- 节点 1 和 2 都有指向节点 0 的边，节点 0 的边积分等于 1 + 2 = 3 。
- 节点 0 和 3 都有指向节点 2 的边，节点 2 的边积分等于 0 + 3 = 3 。
节点 0 和 2 的边积分都是 3 。由于节点 0 的编号更小，返回 0 。

 

提示：

• n == edges.length
• 2 <= n <= 105
• 0 <= edges[i] < n
• edges[i] != i

解题方法：模拟

遍历每条边，假设边$i$的值为$a$，就令$score[a]+=i$。

其中$score$是一个分数数组，默认值全部为$0$。

最终返回所有分数中最大的（若有同样大的则返回编号较小的那个）即为答案。

• 时间复杂度$O(len(edges))$
• 空间复杂度$O(len(edges))$

AC代码

C++

typedef long long ll;
class Solution {
public:
    int edgeScore(vector<int>& edges) {
        vector<ll> score(edges.size());
        ll M = 0;
        int ans = -1;
        for (int i = 0; i < edges.size(); i++) {
            score[edges[i]] += i;
            if (score[edges[i]] > M) {
                M = score[edges[i]];
                ans = edges[i];
            } else if (score[edges[i]] == M) {
                ans = min(ans, edges[i]);
            }
        }
        return ans;
    }
};

Python

from typing import List

class Solution:
    def edgeScore(self, edges: List[int]) -> int:
        scores = [0] * len(edges)
        M, ans = 0, -1
        for edge, th in enumerate(edges):
            scores[th] += edge
            if scores[th] > M or scores[th] == M and th < ans:
                M, ans = scores[th], th
        return ans

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~

Tisfy：https://letmefly.blog.csdn.net/article/details/142433653