数据结构和算法之树形结构(2)

文章出处：数据结构和算法之树形结构(2)

关注码农爱刷题，看更多技术文章！！

三、二叉查找树(接前篇)

二叉查找树，又称二叉搜索树或二叉排序树，是在普通二叉树基础上为了实现快速查找而设计出来的一种树形结构。二叉查找树要求每个节点在树中的任意一个节点，其左子树中的每个节点的值都要小于这个节点的值，而右子树节点的值都大于这个节点的值。引进二叉查找树，是为了更高效地实现二叉树的查找和节点的增删，下图是典型的二叉查找树：

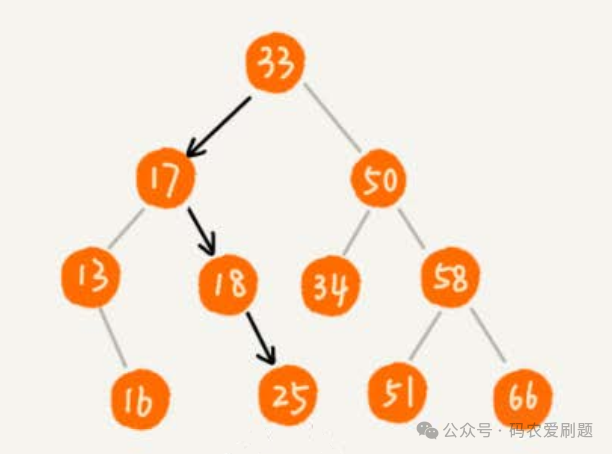
通过中序遍历，我们很容易得到一个按值大小排序的数据序列：13,16,17,18,25,33,34,50,51,58,66。正是这样一个按值大小排序的数据序列，让二叉树节点的查找和增删变得更加高效：当查询一个节点值时，可以从根节点开始比较。如果目标值小于当前节点值，则搜索左子树；如果目标值大于当前节点值，则搜索右子树。这样理论上，每次比较都可以排除掉一半的子树，而不需要遍历整个二叉树。特别是数据集足够大并且查询频繁发生，使用二叉查找树会显著提高性能，理想的情况下二叉查找树的时间复杂度可达到 O(log n)。接下来我们详细介绍二叉查找树的各种操作的实现：

二叉查找树的查找操作

二叉查找树的查找其实逻辑也很简单，如前文所述：从根节点开始查找，如果目标值小于根节点值，则搜索左子树；如果目标值大于根节点值，则搜索右子树，以此类推；下面代码通过循环和递归两种方式实现了查找逻辑：


public class BinaryTreeFind {

    private Node tree; //假设已初始化树及节点

    public Node find(int data) {
        Node p = tree;
        while (p != null) {
            if (data < p.data){
              p = p.leftNode;
            } else if (data > p.data) {
              p = p.rightNode;
            } else {
              return p;
            }
        }
        return null;
    }
    
    public Node find2(int data) {  
        if (tree != null){        
          if (data < tree.data) {
             tree = tree.leftNode;
             return find2(data);
          } else if (data > p.data) {
             tree  = tree.rightNode;
             return find2(data);
          } else {
             return p;
          }   
        }    
        return null;
    }


    class Node {
        private int data;
        private Node leftNode;
        private Node rightNode;

        public Node(int data) {
            this.data = data;
        }
    }
    
   
}

二叉查找树的插入操作

二叉查找树的插入，是以二叉查找树的查找为前提的，因为二叉查找树是一棵有顺序的树，你需要先找到要插入数据在二叉查找树的顺位。具体的逻辑是：从根节点点开始进行比较，小于根结点则与根结点的左子树进行比较，否则与右子树进行比较，直到左子树为空或右子树为空，则插入到相应为空的位置，代码如下：


/**
 * 插入操作
 *
 * @param data
 * @return
 */
public Boolean insert(int data) {
    if (tree == null) {
        tree = new Node(data);
        return true;
    }
    Node p = tree;
    while (p != null) {
        if (data > p.data) {
            // 插入右节点
            if (p.rightNode == null) {
                p.rightNode = new Node(data);
                return true;
            }
            p = p.rightNode;
        } else {
            // 插入 左节点
            if (p.leftNode == null) {
                p.leftNode = new Node(data);
                return true;
            }
            p = p.leftNode;
        }
    }
    return false;
}

二叉查找树的删除操作

二叉查找树的删除，相比二叉查找树查找和插入稍显复杂，需要区分三种情况，具体逻辑如下表：

上表中真正稍显复杂的是第三种场景：删除节点有两子节点的场景。这里稍作说明：二叉查找树的特点是，父节点的值大于左子树所有节点的值，少于右子树所有节点的值，用右子树的最小节点替代删除节点，符合二叉查找树的特点和规范；右子树最小节点既然替换到删除节点的位置，原本位置的最小节点自然要删除，而最小节点通常是子树最下层最左边的叶子节点，不再有子节点，因而直接把其父节点指向它的指针置为Null即完成了它的删除。代码如下：


/**
 * 删除
 * @param data
 */
public void delete(int data) {
    // p指向要删除的节点，初始化指向根节点
    Node p = tree;
    // pp记录的是p的父节点
    Node pp = null;

    // 查找要删除的节点位置，及其父节点
    while (p != null && p.data != data) {
        pp = p;
        if (data > p.data) {
            p = p.rightNode;
        } else {
            p = p.leftNode;
        }
    }
    if (p == null) {
        return;// 没有找到
    }
    // 要删除的节点有两个子节点
    if (p.leftNode != null && p.rightNode != null) {
        // 查找右子树中最小节点
        Node minp = p.rightNode;
        Node minpp = p; // minPP表示minP的父节点
        while (minp.leftNode != null) {
            minpp = minp;
            minp = minp.leftNode;
        }
        // 将 minp 的数据替换到 p 中
        p.data = minp.data;
        // 下面就变成了删除 minp 了
        p = minp;
        pp = minpp;
    }
    // 删除节点是叶子节点或者仅有一个子节点
    Node child; // p 的子节点
    if (p.leftNode != null) {
        child = p.leftNode;
    } else if (p.rightNode != null) {
        child = p.rightNode;
    } else {
        child = null;
    }
    if (pp == null) {
        // 删除的是根节点
        tree = child;
    } else if (pp.leftNode == p) {
        pp.leftNode = child;
    } else {
        pp.rightNode = child;
    }
}

//前述代码来源：https://www.cnblogs.com/xiexiandong/p/13060094.html

关于二叉查找树的删除，有些文章建议不作物理删除，直接标记删除状态只做逻辑删除，这样处理虽然会额外占用一定内存但确实效率会更高，至于哪种方案更好还是需要结合具体的业务场景来判断。

二叉查找树的时间复杂度分析

文章前述内容提到理想情况下，二叉查找树的时间复杂度可以达到O(logn)，那什么是最理想的情况，什么又是最坏的情况呢？我们先看正常情况下，二叉查找树的时间复杂度的推算过程：

上表中N代表二叉查找树的节点总数，K代表时间复杂度(时间复杂度本质上就是计算基本语句的执行次数，基本语句指算法中执行次数最多的语句，具体到这里指的是查询比较语句)；而剩余待查节点数只会随着K的增大而逐步减少直到命中目标节点的上一层等于1，也就是待查剩余节点数=N/(2^K) >= 1，我们计算时间复杂度总是以最坏的情况计算，也就是查到剩余最后一个数才是我们想要的计算的场景，那么得出 N / (2^K) = 1，由此再推算出N = 2^K，再推出K =log2(N)，即最后可推出二叉查找树剩余待查节点的查找时间复杂度为：O(log2(N)) => O(logN)。

在上述推断的过程中，其实隐含一个前提条件，那就是该二叉查找树是一棵满二叉树(关于满二叉树的知识，可参看前述文章数据结构和算法之树形结构(1))，只有是在满二叉树的情况下，剩余待查节点数才会满足上表场景：第一次查询比较后是N/2，第二次查询比较后是N/(2^2) ......；我们假设另一种情况，假设二叉查找树是下列极端情况，如图：

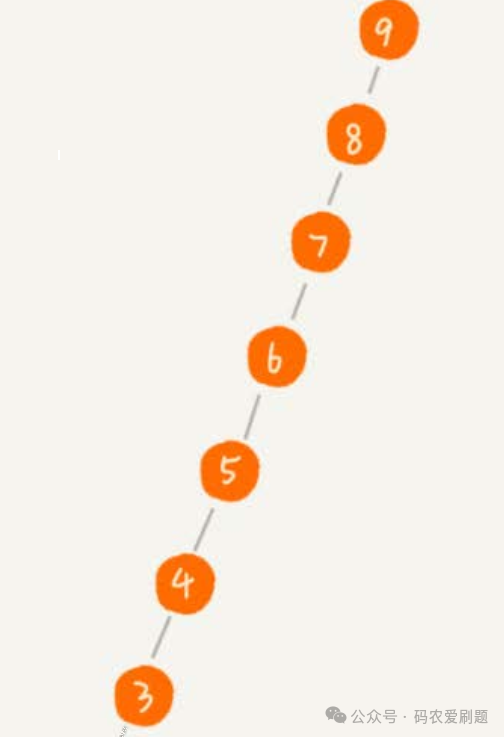
这时再去推算它的查找时间复杂度则如下表：

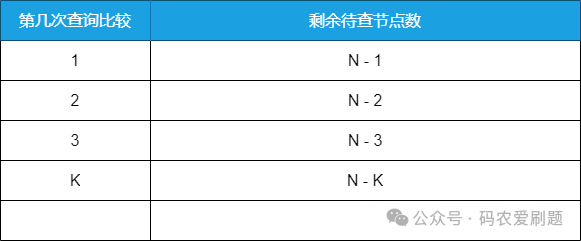
因为此时二叉查找树基本已经退化成一个链表，每一层只有一个节点，每查询比较一次，剩余待查节点数减1，之前的 N / (2^K) 公式已经不再适用(自己细细琢磨)；根据前述的推断逻辑，上表中N - K = 1可推出此时二叉查找树剩余待查节点的查找时间复杂度为：K = O(N)，正是链表的时间复杂度(关于链表结构，可以参看前述文章数据结构和算法之线性结构)。

所以综上所述，二叉查找树时间复杂度最理想的情况是该二叉查找树是一棵满二叉树或者形态接近满二叉树，而最坏的情况是该二叉查找树退化成了一个链表。

那讲到这里，你可能还会有疑惑？假设上面的满二叉查找树和已退化成链表的二叉查找树层数都为5，而要查询的节点都在第5层，按上面的公式两者命中的时间复杂度K不都等于5吗？那时间复杂度是O(N)和O(logN)又有什么区别呢？这里我想说的是，要比较时间复杂度的效率和优劣，应该是在处理同等数据规模的场景下去比较才有意义，例如我们把前面已经退化成链表的二叉查找树转化成下图的满二叉查树：

这时两者节点数相等，我们再来查找同一节点5，你会发现满二叉查找树场景下命中的时间复杂度K为3，而链表场景下命中的时间复杂度K依然为5，从这个对比也不难看出，二叉查找树的时间复杂度和其树的层数或者高度成正比，而满二叉查找树之所以在同等数据规模下效率高于链表式二叉查找树，正是因为其树的层数或高度少于链表式二叉查找树。换一种说法就是，满二叉查找树的节点形态左右比较平衡，而链表式二叉查找树则极度不平衡，节点都偏离到了一条链上而导致树的层数或高度增加，从而效率低下。

为了避免二叉查找树的极度不平衡带来的低效率，在数据结构和算法的实际应用中，又衍生出了平衡二叉树，而满二叉查找树正是平衡二叉树的一种特例。关于平衡二叉树的知识，我们将在后续章节继续介绍，特请关注！

码农爱刷题

为计算机编程爱好者和从业人士提供技术总结和分享！为前行者蓄力，为后来者探路！