路径处理 | 关键点提取之Douglas–Peucker算法(附ROS C++/Python实现)

news2024/12/25 1:17:11

0 专栏介绍

🔥课设、毕设、创新竞赛必备！🔥本专栏涉及更高阶的运动规划算法轨迹优化实战，包括：曲线生成、碰撞检测、安全走廊、优化建模(QP、SQP、NMPC、iLQR等)、轨迹优化(梯度法、曲线法等)，每个算法都包含代码实现加深理解

🚀详情：运动规划实战进阶：轨迹优化篇

1 路径关键点提取

路径关键点提取也称为路径降采样，在路径规划中主要用于简化和优化路径表示。一方面，路径降采样可以去除冗余点，从而减少路径中的采样点数量，减小数据存储和传输的成本；另一方面，在路径跟踪和导航时，较少的点可以提高计算效率，减少实时处理的负担。在环境噪声敏感型的算法中，简化路径保留了路径的关键特征和形状，而滤除了噪点，可以增强在执行过程中对微小抖动或误差的鲁棒性

2 道格拉斯-普克算法Douglas–Peucker

道格拉斯-普克算法(Douglas–Peucker)是一种经典的路径关键点提取算法，其基于分治思想，以采样前后路径误差最小化为目标，提取路径关键点。

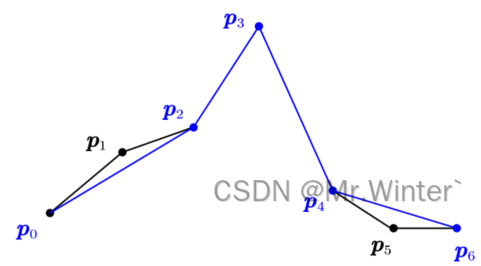
以下图为例阐述算法原理

初始给定一组有序的路径点列 $\left\{ \boldsymbol{p} \right\} _{0}^{N-1}$ 与误差阈值 $\delta$ ，其中 $N$ 是路径点数；
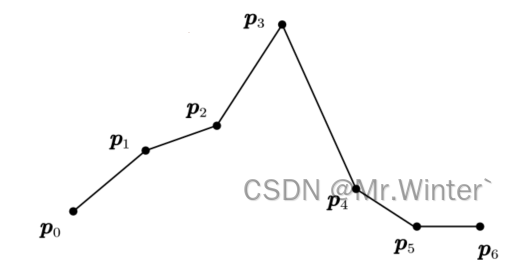
以路径首末点组成的 $\boldsymbol{p}_0\boldsymbol{p}_{N-1}$ 为初始待处理线段，查找 $\boldsymbol{p}_0\boldsymbol{p}_{N-1}$ 之间的点列中离 $\boldsymbol{p}_0\boldsymbol{p}_{N-1}$ 最远的点，并判断该距离 $d$ 是否大于阈值 $\delta$ ，若 $d>\delta$ 则说明该点不能剪枝(否则剪枝前后曲线误差超过预期)；若 $\le \delta$ 则说明该点可以忽略；如图所示需要保留 $\boldsymbol{p}_3$ ；

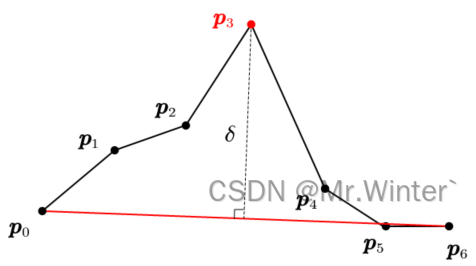
在这里插入图片描述

对需要保留的节点进行分治，重复步骤(2)直到遍历结束；如图所示，分别以 $\boldsymbol{p}_0\boldsymbol{p}_3$ 、 $\boldsymbol{p}_3\boldsymbol{p}_{N-1}$ 为待处理线段进行递归

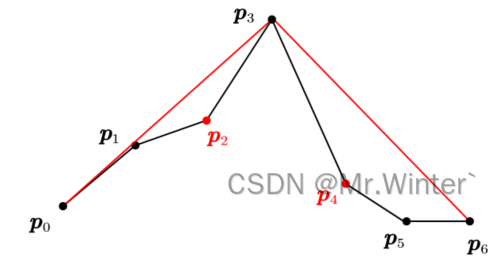
在这里插入图片描述

最终得到剪枝后的路径点列如图所示

在这里插入图片描述

3 算法实现与可视化

3.1 ROS C++仿真

核心代码如下所示

void RDP::process(const rmp::common::geometry::Points2d& path_in, rmp::common::geometry::Points2d& path_out)
{
  path_out.clear();
  int max_idx = -1;
  double max_dist = -1.0;
  int path_size = static_cast<int>(path_in.size());
  rmp::common::geometry::LineSegment2d line({ path_in[0].x(), path_in[0].y() },
                                            { path_in[path_size - 1].x(), path_in[path_size - 1].y() });
  for (int i = 1; i < path_size - 1; i++)
  {
    double d = line.distanceTo({ path_in[i].x(), path_in[i].y() });
    if (d > max_dist)
    {
      max_dist = d;
      max_idx = i;
    }
  }

  if (max_dist > delta_)
  {
    rmp::common::geometry::Points2d left_pts, right_pts;
    left_pts.reserve(max_idx + 1);
    right_pts.reserve(path_size - max_idx);
    for (int i = 0; i <= max_idx; i++)
    {
      left_pts.emplace_back(path_in[i].x(), path_in[i].y());
    }
    for (int i = max_idx; i < path_size; i++)
    {
      right_pts.emplace_back(path_in[i].x(), path_in[i].y());
    }

    rmp::common::geometry::Points2d left_result, right_result;
    process(left_pts, left_result);
    process(right_pts, right_result);
    path_out.insert(path_out.end(), left_result.begin(), left_result.end() - 1);
    path_out.insert(path_out.end(), right_result.begin(), right_result.end());
  }
  else
  {
    path_out.emplace_back(path_in[0].x(), path_in[0].y());
    path_out.emplace_back(path_in[path_size - 1].x(), path_in[path_size - 1].y());
  }
}

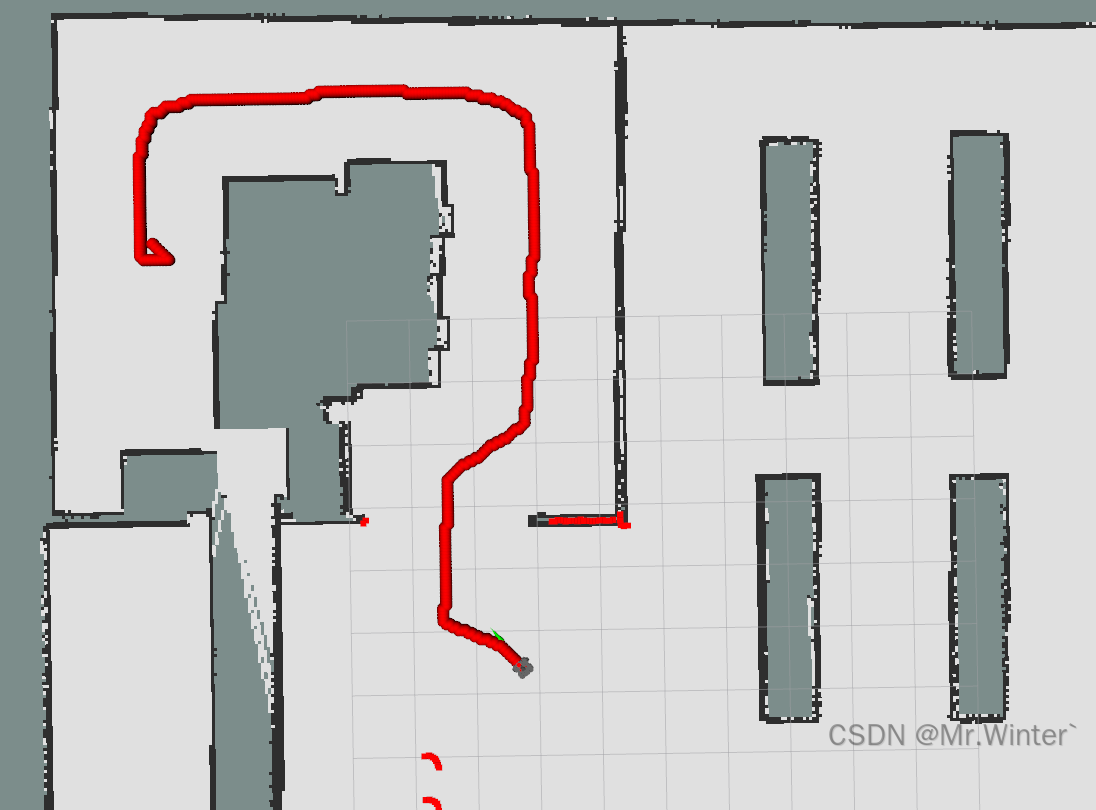
我们用红色的原点表示路径点，绿色曲线段表示路径。下面显示的是未处理的路径点，因为地图栅格分辨率是 $0.05 m$ ，所以看起来非常稠密

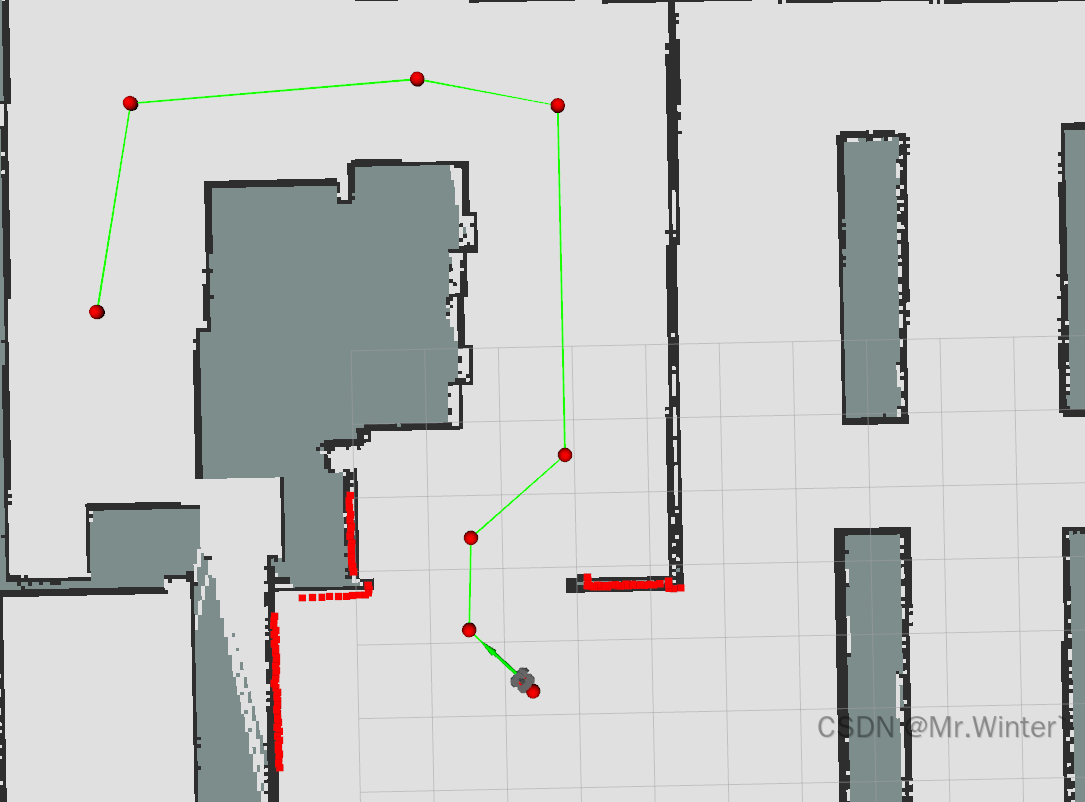
在这里插入图片描述

经过算法剪枝后的路径如下所示，可以看到既保留了原始路径的几何特征，又大幅度降低了路径冗余度

在这里插入图片描述

3.2 Python仿真

核心代码如下所示：

def rdp_rec(M, epsilon, dist=pldist):
    dmax = 0.0
    index = -1

    for i in xrange(1, M.shape[0]):
        d = dist(M[i], M[0], M[-1])

        if d > dmax:
            index = i
            dmax = d

    if dmax > epsilon:
        r1 = rdp_rec(M[:index + 1], epsilon, dist)
        r2 = rdp_rec(M[index:], epsilon, dist)

        return np.vstack((r1[:-1], r2))
    else:
        return np.vstack((M[0], M[-1]))