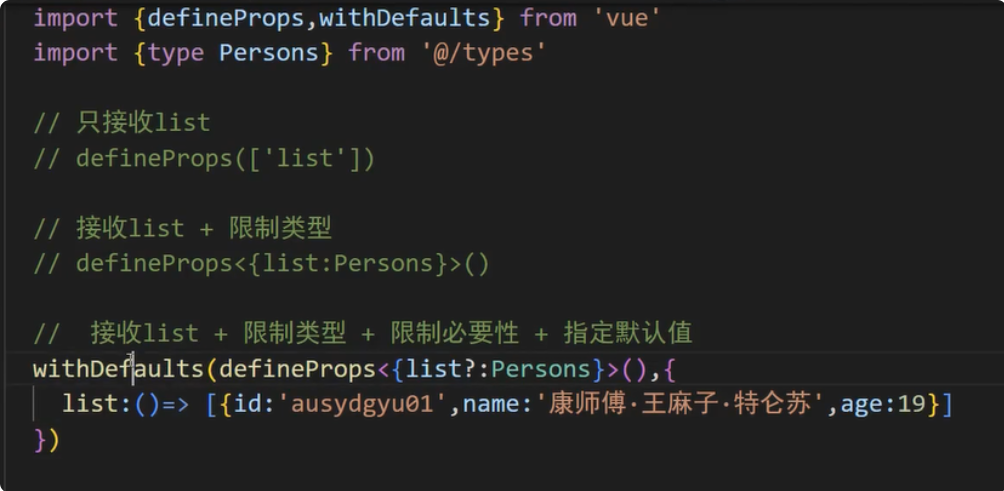
有了并行K简化的概念及其属性，以及其在LEAN类型理论中的相关证明，就可以证明，在K简化下的Church-Rosser 定理。即：

        其过程如下：

        证明如下：

其中的 lemma 4.9 和 4.10 ，及 4.8 是

        这整个证明过程还是挺清晰明了的，就是需要对不同的规则进行归纳分析。

K简化下的定义上相等，记 ≡ₖ

        然后，定义一个新的概念，K简化下的定义上相等，记 ≡ₖ ，即表示，两表达式在经过K简化后在证据不区分下定义上相等。这个，在

        具体定义如下：

        其中

        证明过程请查看那原文，这里也不多赘述了。

        由此，有

        证明过程请查看那原文，这里也不多赘述了。

        这样，就证明了 n-provability 是 定义上反向的。

        根据

        证明了赋型唯一性，即

        其全过程，可以回顾赋型唯一性的证明过程简介。

        也就是说，在LEAN类型系统里，每个表达式（Expression）有且只有一个定义上相等的类型（Type）。