LeetCode 每周算法 6(图论、回溯)
图论算法:

class Solution:
def dfs(self, grid: List[List[str]], r: int, c: int) -> None:
"""
深度优先搜索函数,用于遍历并标记与当前位置(r, c)相连的所有陆地
(即值为"1"的格子)为已访问(即标记为0)。
:param grid: 二维网格,其中的每个元素都是'0'或'1'。
:param r: 当前遍历到的行索引。
:param c: 当前遍历到的列索引。
"""
grid[r][c] = '0' # 将当前位置标记为已访问(即陆地变为水)
nr, nc = len(grid), len(grid[0]) # 获取网格的行数和列数
# 遍历当前位置的上下左右四个相邻位置
for x, y in [(r - 1, c), (r + 1, c), (r, c - 1), (r, c + 1)]:
# 检查相邻位置是否在网格范围内且为陆地(即值为'1')
if 0 <= x < nr and 0 <= y < nc and grid[x][y] == "1":
self.dfs(grid, x, y) # 递归地遍历相邻的陆地
def numIslands(self, grid: List[List[str]]) -> int:
"""
计算给定网格中的岛屿数量。
:param grid: 二维网格,其中的每个元素都是'0'或'1'。
:return: 网格中的岛屿数量。
"""
nr = len(grid)
if nr == 0: # 如果网格为空,则岛屿数量为0
return 0
nc = len(grid[0]) # 获取网格的列数
num_islands = 0 # 初始化岛屿数量为0
for r in range(nr): # 遍历网格的每一行
for c in range(nc): # 遍历网格的每一列
if grid[r][c] == "1": # 如果当前位置是陆地
num_islands += 1 # 岛屿数量加1
self.dfs(grid, r, c) # 调用dfs函数遍历并标记与当前陆地相连的所有陆地
return num_islands # 返回岛屿数量

class Solution:
def orangesRotting(self, grid: List[List[int]]) -> int:
R, C = len(grid), len(grid[0]) # 获取网格的行数和列数
# 初始化一个队列,用于存放腐烂橙子(值为2)的位置及其腐烂时间(初始为0)
queue = deque()
for r, row in enumerate(grid):
for c, val in enumerate(row):
if val == 2:
queue.append((r, c, 0))
# 定义一个辅助函数,用于生成当前橙子位置(r, c)的上下左右四个相邻位置
def neighbors(r, c):
for nr, nc in ((r - 1, c), (r, c - 1), (r + 1, c), (r, c + 1)):
if 0 <= nr < R and 0 <= nc < C: # 确保相邻位置在网格范围内
yield nr, nc
d = 0 # 初始化腐烂时间计数器
while queue: # 当队列不为空时,继续执行
r, c, d = queue.popleft() # 从队列中取出腐烂橙子的位置及其腐烂时间
for nr, nc in neighbors(r, c): # 遍历当前腐烂橙子的四个相邻位置
if grid[nr][nc] == 1: # 如果相邻位置是新鲜的橙子
grid[nr][nc] = 2 # 将其标记为腐烂的橙子
queue.append((nr, nc, d + 1)) # 将其加入队列,并更新腐烂时间为当前时间+1
# 检查网格中是否还有新鲜的橙子(值为1)
if any(1 in row for row in grid):
return -1 # 如果有,说明无法让所有橙子都腐烂,返回-1
return d # 否则,返回最后的腐烂时间

class Solution:
def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
# 创建一个defaultdict来存储课程的邻接表,即每个课程的后继课程列表
edges = collections.defaultdict(list)
# 创建一个列表来存储每个课程的入度(即有多少课程是该课程的前置课程)
indeg = [0] * numCourses
# 遍历先决条件列表,构建邻接表和入度列表
for info in prerequisites:
# info[1] 是当前课程,info[0] 是其前置课程
# 将当前课程(info[1])的后继课程(info[0])添加到邻接表中
edges[info[1]].append(info[0])
# 将前置课程(info[0])的入度加1
indeg[info[0]] += 1
# 创建一个双端队列,用于存储入度为0的课程(即没有前置课程的课程)
q = collections.deque([u for u in range(numCourses) if indeg[u] == 0])
# 初始化已访问(或已完成)的课程数
visited = 0
# 使用广度优先搜索(BFS)遍历课程
while q:
# 每从队列中取出一个课程,表示该课程可以完成
visited += 1
u = q.popleft()
# 遍历当前课程的所有后继课程
for v in edges[u]:
# 将后继课程的入度减1,表示完成了一个前置课程
indeg[v] -= 1
# 如果后继课程的入度变为0,说明其所有前置课程都已完成,可以加入队列继续搜索
if indeg[v] == 0:
q.append(v)
# 如果已访问的课程数等于总课程数,说明所有课程都可以完成
# 否则,存在环,无法完成所有课程
return visited == numCourses

class Trie:
def __init__(self):
# 初始化Trie节点,children是一个长度为26的列表,
# 用于存储指向子节点的引用(假设只处理小写字母a-z)
# 每个位置对应一个字母(例如,0对应'a',1对应'b',...,25对应'z')
# isEnd用于标记该节点是否是某个单词的结尾
self.children = [None] * 26
self.isEnd = False
def searchPrefix(self, prefix: str) -> "Trie":
# 搜索并返回给定前缀对应的最后一个Trie节点
# 如果前缀不存在于Trie中,则返回None
node = self # 从根节点开始搜索
for ch in prefix:
# 将字符转换为对应的索引('a'->0, 'b'->1, ..., 'z'->25)
ch = ord(ch) - ord("a")
# 如果当前节点的children中对应字符的节点不存在,说明前缀不存在,返回None
if not node.children[ch]:
return None
# 否则,移动到子节点继续搜索
node = node.children[ch]
# 如果所有字符都成功匹配,返回最后一个节点
return node
def insert(self, word: str) -> None:
# 将一个单词插入到Trie中
node = self # 从根节点开始插入
for ch in word:
# 将字符转换为对应的索引
ch = ord(ch) - ord("a")
# 如果当前节点的children中对应字符的节点不存在,则创建一个新的Trie节点
if not node.children[ch]:
node.children[ch] = Trie()
# 移动到子节点继续插入
node = node.children[ch]
# 标记最后一个节点为单词的结尾
node.isEnd = True
def search(self, word: str) -> bool:
# 搜索Trie中是否存在一个完整的单词
# 使用searchPrefix找到最后一个节点,然后检查该节点是否是某个单词的结尾
node = self.searchPrefix(word)
return node is not None and node.isEnd
def startsWith(self, prefix: str) -> bool:
# 检查Trie中是否存在以给定前缀开头的单词
# 使用searchPrefix找到最后一个节点,如果找到,则说明存在以该前缀开头的单词
return self.searchPrefix(prefix) is not None
# Your Trie object will be instantiated and called as such:
# obj = Trie()
# obj.insert(word)
# param_2 = obj.search(word)
# param_3 = obj.startsWith(prefix)
图论算法:

class Solution {
public:
// 回溯函数,用于生成所有排列
// res: 存储所有排列的二维向量
// output: 当前排列的向量,通过修改它来生成新的排列
// first: 当前需要确定位置的索引(从0开始)
// len: 输入数组nums的长度,即需要排列的元素总数
void backtrack(vector<vector<int>>& res, vector<int>& output, int first, int len) {
// 如果已经处理完所有元素(即已经填充了所有位置),则将当前排列添加到结果中
if (first == len) {
// 使用emplace_back直接在res的末尾构造一个output的副本
res.emplace_back(output);
return;
}
// 从first开始,遍历所有未确定位置的元素
for (int i = first; i < len; ++i) {
// 将当前位置的元素与first位置的元素交换,
// 这样可以尝试将不同的元素放在first位置
swap(output[i], output[first]);
// 递归地处理下一个位置(first+1)
backtrack(res, output, first + 1, len);
// 回溯,撤销上一步的交换,以便尝试其他可能性
swap(output[i], output[first]);
}
}
// 公开接口,用于生成给定数组nums的所有排列
// nums: 需要排列的整数数组
// 返回值: 包含所有排列的二维向量
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int>> res; // 初始化结果向量
// 从第一个元素开始回溯,直到处理完所有元素
backtrack(res, nums, 0, (int)nums.size());
return res; // 返回所有排列的集合
}
};

// 迭代法实现子集枚举
class Solution {
public:
// 用于临时存储当前子集的结果
vector<int> output;
// 用于存储所有子集的结果
vector<vector<int>> ans;
// 生成给定整数数组nums的所有子集
vector<vector<int>> subsets(vector<int>& nums) {
// 遍历所有可能的位掩码,从0到2^nums.size() - 1
// 每个位掩码都代表一个子集,其中1表示选择该位置的元素,0表示不选择
for (int mask = 0; mask < (1 << nums.size()); ++mask) {
// 清空output,为构建新的子集做准备
output.clear();
// 遍历nums中的每个元素及其对应的位掩码位
for (int i = 0; i < nums.size(); ++i) {
// 如果mask的第i位是1(即mask & (1 << i)不为0),则将nums[i]加入当前子集
if (mask & (1 << i)) {
output.push_back(nums[i]);
}
}
// 将构建好的子集添加到结果集中
ans.push_back(output);
}
// 返回包含所有子集的结果集
return ans;
}
};
// 递归法实现子集枚举
// class Solution {
// public:
// vector<int> output; // 用于临时存储当前子集的结果
// vector<vector<int>> ans; // 用于存储所有子集的结果
// // 回溯函数,从数组的第first个元素开始构建子集
// // first 表示当前正在处理的元素在nums中的索引
// // nums 是给定的整数数组
// void backtrack(int first, vector<int>& nums) {
// // 如果已经处理了nums中的所有元素,则将当前子集添加到结果集中
// if (first == nums.size()) {
// ans.push_back(output);
// return;
// }
// // 选择当前元素加入子集
// output.push_back(nums[first]);
// // 递归处理下一个元素,继续构建子集
// backtrack(first + 1, nums);
// // 回溯,撤销选择当前元素,尝试不包含当前元素的情况
// output.pop_back();
// backtrack(first + 1, nums);
// }
// // 主函数,用于生成nums的所有子集
// vector<vector<int>> subsets(vector<int>& nums) {
// backtrack(0, nums);
// return ans;
// }
// };

class Solution {
public:
// 主函数,用于生成给定数字字符串的所有字母组合
vector<string> letterCombinations(string digits) {
if (digits.empty()) { // 如果输入的数字字符串为空,则直接返回空的组合列表
return combinations;
}
string combination; // 用于存储当前正在构建的字母组合
vector<string> combinations; // 存储所有可能的字母组合
// 创建一个哈希表,将数字映射到它们对应的字母字符串
unordered_map<char, string> phoneMap{
{'2', "abc"},
{'3', "def"},
{'4', "ghi"},
{'5', "jkl"},
{'6', "mno"},
{'7', "pqrs"},
{'8', "tuv"},
{'9', "wxyz"}
};
// 调用回溯函数来生成所有可能的组合
backtrack(combinations, phoneMap, digits, 0, combination);
return combinations; // 返回所有生成的字母组合
}
// 回溯函数,用于递归地生成所有可能的字母组合
void backtrack(vector<string>& combinations, const unordered_map<char, string>& phoneMap, const string& digits, int index, string& combination) {
if (index == digits.length()) { // 如果已经处理完所有数字,则将当前组合添加到结果列表中
combinations.push_back(combination);
} else {
char digit = digits[index]; // 获取当前正在处理的数字
const string& letters = phoneMap.at(digit); // 从哈希表中获取该数字对应的字母字符串
for (const char& letter: letters) { // 遍历该数字对应的所有字母
combination.push_back(letter); // 将当前字母添加到当前组合中
// 递归调用回溯函数,处理下一个数字,同时传入更新后的组合
backtrack(combinations, phoneMap, digits, index + 1, combination);
combination.pop_back(); // 回溯,撤销上一步的添加操作,以便尝试下一个字母
}
}
}
};

class Solution {
public:
// 用于存储所有可能的组合结果的向量
vector<vector<int>> result;
// 用于在回溯过程中构建当前路径的向量
vector<int> path;
// 回溯函数,用于生成所有可能的组合
// candidates: 候选数字的集合
// target: 目标值,需要找到的和
// start: 从哪个候选数字开始考虑(避免重复使用相同的数字)
void backtrack(const vector<int>& candidates, int target, int start) {
// 如果当前目标和已经小于0,说明当前路径不可行,直接返回
if (target < 0) return;
// 如果目标和为0,说明找到了一个有效的组合,将其添加到结果中
if (target == 0) {
result.push_back(path);
return;
}
// 遍历候选数字,从start开始,确保不重复使用数字,并且当前数字不超过目标和
for (int i = start; i < candidates.size() && target - candidates[i] >= 0; i++) {
// 将当前数字添加到路径中
path.push_back(candidates[i]);
// 递归调用,目标值减去当前数字,start仍为i,因为可以重复使用相同的数字
// 注意:在某些问题中,可能需要将start改为i+1来避免重复使用相同的数字
backtrack(candidates, target - candidates[i], i);
// 回溯,撤销选择,继续尝试其他可能
path.pop_back();
}
}
// 主函数,用于找到所有可以使数字和为target的组合
// candidates: 候选数字的集合
// target: 目标值
// 返回值: 所有可能的组合
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
// 对候选数字进行排序,这有助于在回溯过程中剪枝,提高效率
// 特别是当允许重复使用数字时,排序可以确保较小的数字先被考虑
sort(candidates.begin(), candidates.end());
// 调用回溯函数开始搜索
backtrack(candidates, target, 0);
// 返回所有找到的组合
return result;
}
};

class Solution {
// 回溯函数,用于生成所有有效的括号组合
// result: 存储所有有效括号组合的字符串向量
// current: 当前正在构建的括号字符串
// left: 当前已使用的左括号数量
// right: 当前已使用的右括号数量
// n: 目标括号对的数量
void backtrack(vector<string>& result, string& current, int left, int right, int n) {
// 如果当前括号字符串的长度达到了目标长度(n对括号即2n个字符)
// 则将其添加到结果向量中
if (current.size() == n * 2) {
result.push_back(current);
return;
}
// 如果还可以添加左括号(即左括号数量小于n)
if (left < n) {
current.push_back('('); // 添加左括号
backtrack(result, current, left + 1, right, n); // 递归调用,左括号数量+1
current.pop_back(); // 回溯,撤销上一步的操作
}
// 如果右括号数量小于左括号数量(保证括号的有效性)
if (right < left) {
current.push_back(')'); // 添加右括号
backtrack(result, current, left, right + 1, n); // 递归调用,右括号数量+1
current.pop_back(); // 回溯,撤销上一步的操作
}
}
public:
// 生成所有可能的、且有效的括号组合的公共接口
// n: 括号对的数量
vector<string> generateParenthesis(int n) {
vector<string> result; // 存储结果的向量
string current; // 当前正在构建的括号字符串
backtrack(result, current, 0, 0, n); // 从无括号开始,调用回溯函数
return result; // 返回所有有效的括号组合
}
};
// class Solution {
// bool valid(const string& str) {
// int balance = 0;
// for (char c: str) {
// if (c == '(') {
// ++balance;
// } else {
// --balance;
// }
// if (balance < 0) {
// return false;
// }
// }
// return balance == 0;
// }
// void backtrack(string& current, int n, vector<string>& result) {
// if (n == current.size()) {
// if (valid(current)) {
// result.push_back(current);
// }
// return;
// }
// current += '(';
// backtrack(current, n, result);
// current.pop_back();
// current += ')';
// backtrack(current, n, result);
// current.pop_back();
// }
// public:
// vector<string> generateParenthesis(int n) {
// vector<string> result;
// string current;
// backtrack(current, n * 2, result);
// return result;
// }
// };

class Solution {
public:
// 判断给定单词是否可以通过在棋盘board上相邻位置上的字母连接而成
bool exist(vector<vector<char>>& board, string word) {
// 遍历棋盘上的每一个位置作为起始点
for (int i = 0; i < board.size(); i++) {
for (int j = 0; j < board[0].size(); j++) {
// 为每个起始点创建一个访问标记矩阵,初始都为false
vector<vector<bool>> visited(board.size(), vector<bool>(board[0].size(), false));
// 从当前位置开始,尝试深度优先搜索以找到单词
if (dfs(board, visited, word, 0, i, j)) return true; // 如果找到单词,则返回true
}
}
// 如果遍历完所有起始点都没有找到单词,则返回false
return false;
}
private:
// 深度优先搜索函数,尝试在棋盘上找到单词
bool dfs(vector<vector<char>>& board, vector<vector<bool>>& visited, const string& word, int str_index, int i, int j) {
// 如果已经匹配完单词的所有字符,说明找到了单词,返回true
if (str_index == word.size()) return true;
// 检查当前位置是否越界、是否已访问过、或者是否与单词的当前字符不匹配
// 如果任何一个条件不满足,则无法继续搜索,返回false
if (i >= board.size() || i < 0 ||
j >= board[0].size() || j < 0 ||
visited[i][j] == true || board[i][j] != word[str_index]) return false;
// 标记当前位置为已访问
visited[i][j] = true;
// 尝试向上、下、左、右四个方向搜索
// 如果在任何一个方向上找到了单词,则返回true
if (dfs(board, visited, word, str_index + 1, i + 1, j) || // 向右
dfs(board, visited, word, str_index + 1, i - 1, j) || // 向左
dfs(board, visited, word, str_index + 1, i, j + 1) || // 向下
dfs(board, visited, word, str_index + 1, i, j - 1)) return true; // 向上
// 如果四个方向都没有找到单词,则回溯,将当前位置标记为未访问
visited[i][j] = false;
// 返回false,表示以当前位置为起始点没有找到单词
return false;
}
};

class Solution {
private:
// f是一个二维动态数组,用于存储字符串s中任意子串[i, j]是否为回文串的布尔值
vector<vector<int>> dp;
// result是一个二维字符串向量,用于存储所有满足条件的分割结果,每个内部向量代表一种分割方式
vector<vector<string>> result;
// answer是一个字符串向量,用于在DFS过程中临时存储当前的分割结果
vector<string> answer;
// n表示字符串s的长度
int n;
public:
// 深度优先搜索函数,用于遍历所有可能的分割方式
// s是当前处理的字符串,i是当前遍历到的起始位置
void dfs(const string& s, int i) {
// 如果遍历到了字符串的末尾,说明找到了一种分割方式,将其添加到结果中
if (i == n) {
result.push_back(answer);
return;
}
// 从当前位置i开始,尝试所有可能的分割点j
for (int j = i; j < n; ++j) {
// 如果子串[i, j]是回文串,则进行下一步分割
if (dp[i][j]) {
// 将当前回文子串添加到答案中
answer.push_back(s.substr(i, j - i + 1));
// 递归调用dfs,从j+1位置开始继续搜索
dfs(s, j + 1);
// 回溯,移除刚刚添加的回文子串,以尝试其他可能的分割
answer.pop_back();
}
}
}
// partition函数是类的公开接口,用于找到并返回所有满足条件的分割方式
vector<vector<string>> partition(string s) {
// 初始化n为字符串s的长度
n = s.size();
// 初始化f数组,默认所有子串都是回文串(之后会通过动态规划更新)
dp.assign(n, vector<int>(n, true));
// 使用动态规划计算f数组,即判断所有子串是否为回文串
for (int i = n - 1; i >= 0; --i) {
for (int j = i; j < n; ++j) {
// 如果首尾字符相等且去掉首尾后的子串也是回文串,则当前子串是回文串
dp[i][j] = (s[i] == s[j] && (j - i <= 1 || dp[i + 1][j - 1]));
}
}
// 从字符串的起始位置开始,使用深度优先搜索遍历所有可能的分割方式
dfs(s, 0);
// 返回所有满足条件的分割结果
return result;
}
};
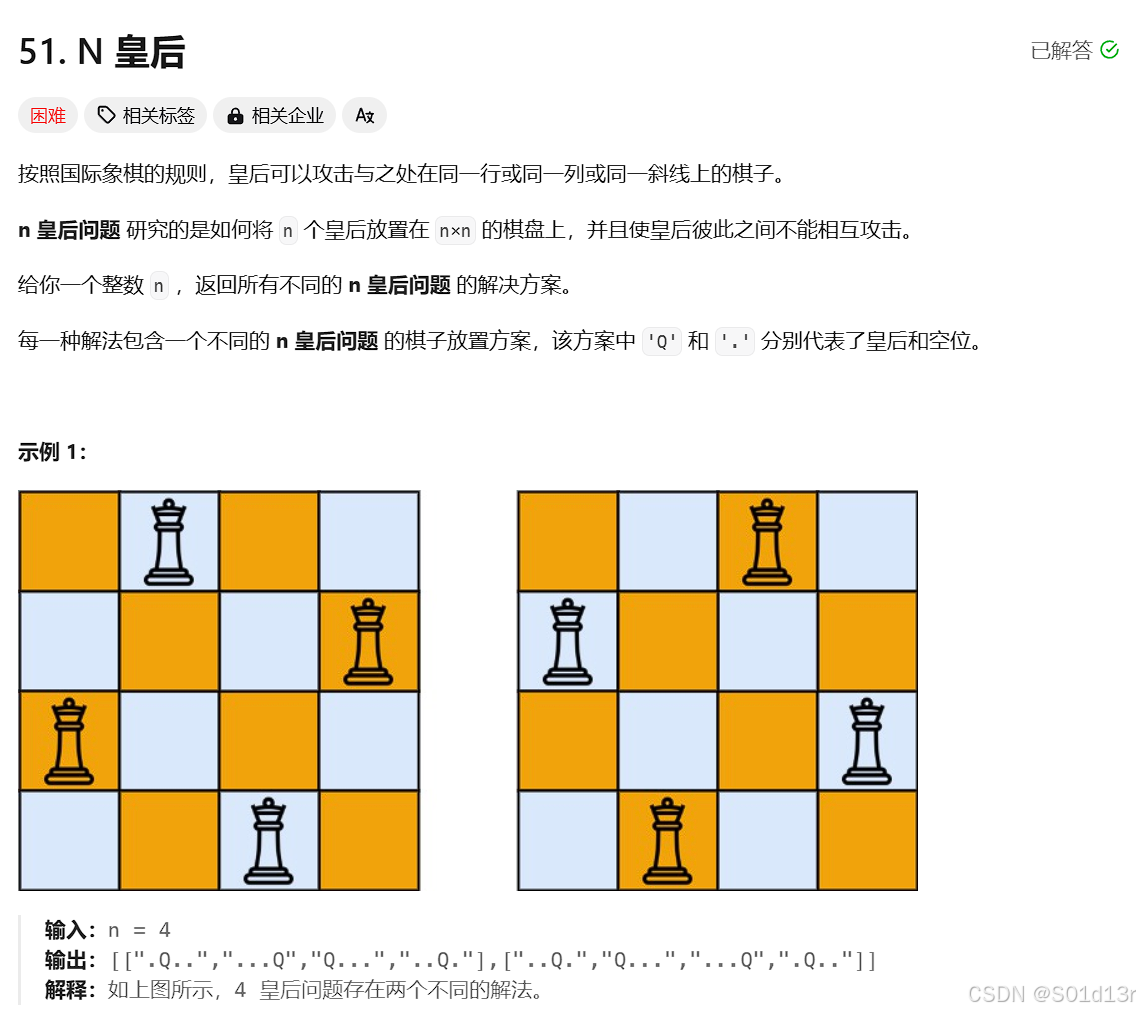
class Solution {
private:
// 用于存储所有有效的N皇后解决方案
vector<vector<string>> result;
// 回溯函数,尝试在每一行放置皇后,并递归地处理下一行
void backtracking(int n, int row, vector<string>& chessboard) {
// 如果已经处理完所有行,说明找到了一个有效的解决方案,将其添加到结果中
if (row == n) {
result.push_back(chessboard);
return;
}
// 遍历当前行的每一列
for (int col = 0; col < n; col++) {
// 检查在当前位置放置皇后是否有效
if (isvalid(row, col, chessboard, n)) {
// 在当前位置放置皇后
chessboard[row][col] = 'Q';
// 递归处理下一行
backtracking(n, row + 1, chessboard);
// 回溯,撤销在当前位置放置的皇后
chessboard[row][col] = '.';
}
}
}
// 检查在(row, col)位置放置皇后是否有效
// 有效的条件是当前位置所在列、左上方对角线、右上方对角线上没有皇后
bool isvalid(int row, int col, vector<string>& chessboard, int n) {
// 检查列上是否有皇后
for (int i = 0; i < row; i++) {
if (chessboard[i][col] == 'Q') {
return false;
}
}
// 检查左上方对角线上是否有皇后
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
// 检查右上方对角线上是否有皇后
for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
// 如果没有冲突,则当前位置有效
return true;
}
public:
// 主函数,用于解决N皇后问题
// 返回所有有效的N皇后解决方案
vector<vector<string>> solveNQueens(int n) {
// 清除之前的结果
result.clear();
// 初始化棋盘,所有位置都是'.'
vector<string> chessboard(n, string(n, '.'));
// 从第一行开始回溯
backtracking(n, 0, chessboard);
// 返回所有有效的解决方案
return result;
}
};