【笔记】自动驾驶预测与决策规划_Part3

文章目录

- 0. 前言
- 1. 基于搜索的路径规划
- - 1.1 A* 算法
  - 1.2 Hybrid A* 算法
- 2. 基于采样的路径规划
- - 2.1 Frenét Frame方法
  - 2.2 Cartesian →Frenét 1D $(x, y)$ —> $(s, l)$
  - 2.3 Cartesian →Frenét 3D
  - 2.4 贝尔曼Bellman最优性原理
  - 2.5 高速轨迹采样——横向
  - 2.6 高速轨迹采样——纵向
  - 2.7 低速轨迹规划——横向
  - 2.8 总结
- 3. 基于优化的路径规划
- - 3.1 以百度Apollo EM planner为例
  - 3.2 M-Step DP Path
  - 3.3 M-Step DP Speed Optimizerp

0. 前言

本文主要记录课程《自动驾驶预测与决策技术》的学习过程，难免会有很多纰漏，感谢指正。
课程链接：https://www.shenlanxueyuan.com/my/course/700

基于搜索的路径规划
基于采样的路径规划
基于优化的路径规划

1. 基于搜索的路径规划

1.1 A* 算法

A*算法是一种用于路径规划和搜索的启发式算法，基于图搜索的思想，结合了深度优先搜索（DFS）和广度优先搜索（BFS）的优点，可以找到从起点到终点的最优路径。

基本原理

A*算法通过维护一个优先队列来存储当前待探索的节点，每次从中选择一个估计总代价最小的节点进行扩展。每个节点的总代价由两个部分组成：

g(n): 从起点到当前节点n的实际代价。这是路径上已经发生的开销，也就是从起点出发，经过一系列已探索的节点，到达当前节点n所花费的总代价。g(n)通常根据具体问题中的距离、时间、能量消耗等进行计算。
h(n): 从节点n到终点的估计代价（通常使用启发式函数计算）

A*算法的核心思想是通过选择最小的f(n)来扩展节点，其中：

$f (n) = g (n) + h (n)$
启发式函数

启发式函数h(n)是关键所在，它估计从当前节点到目标节点的代价。常用的启发式函数包括：

曼哈顿距离: $h(n) = |x_{n} - x_{goal}| + |y_{n} - y_{goal}|$ 适用于网格状地图。
欧几里得距离: $\sqrt{(x_{n} - x_{goal})^2 + (y_{n} - y_{goal})^2}$

启发式函数需要满足一致性或可接受性，即h(n)不会高估实际代价。

A*算法的优点在于通过启发式函数指导搜索，能够高效地找到最优路径。它在自动驾驶中的应用包括动态路径规划，避免障碍物，并实时更新路径以应对道路上的变化。

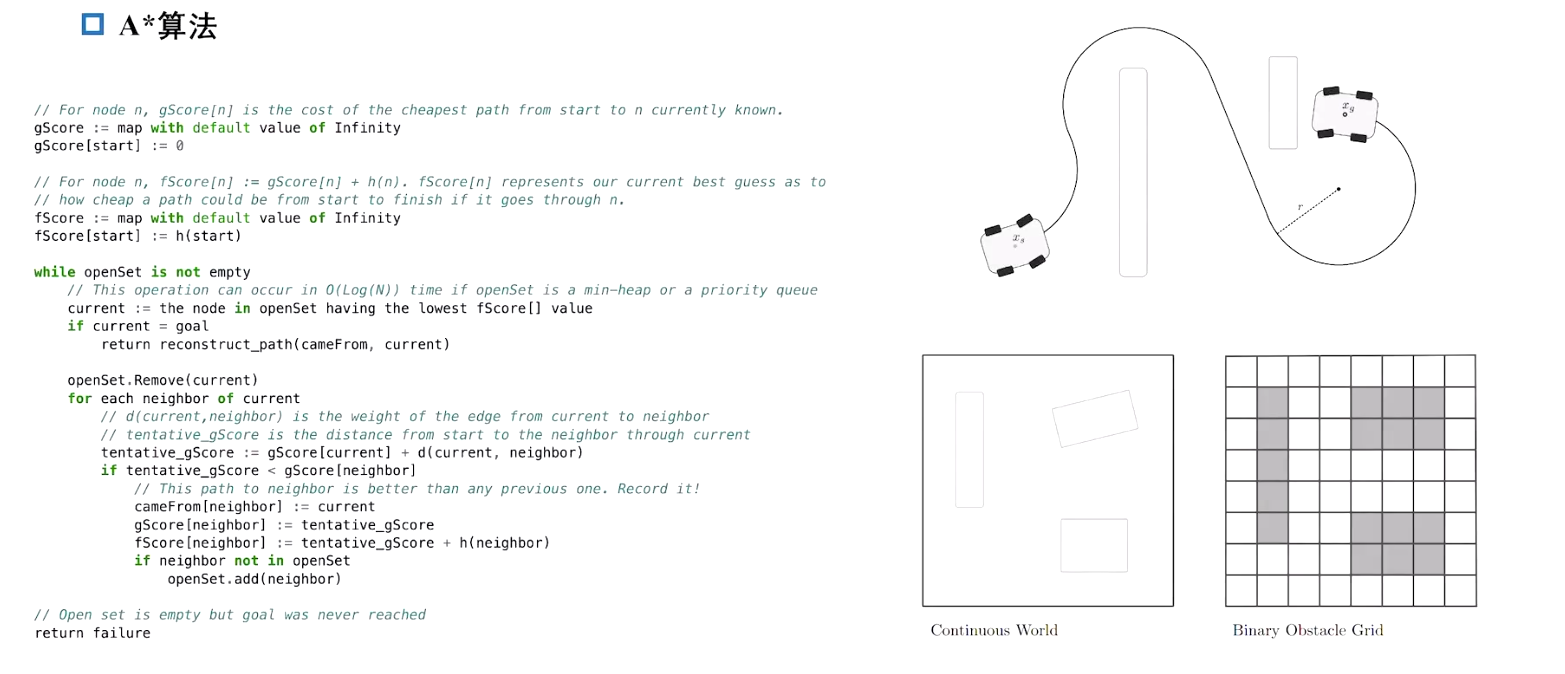
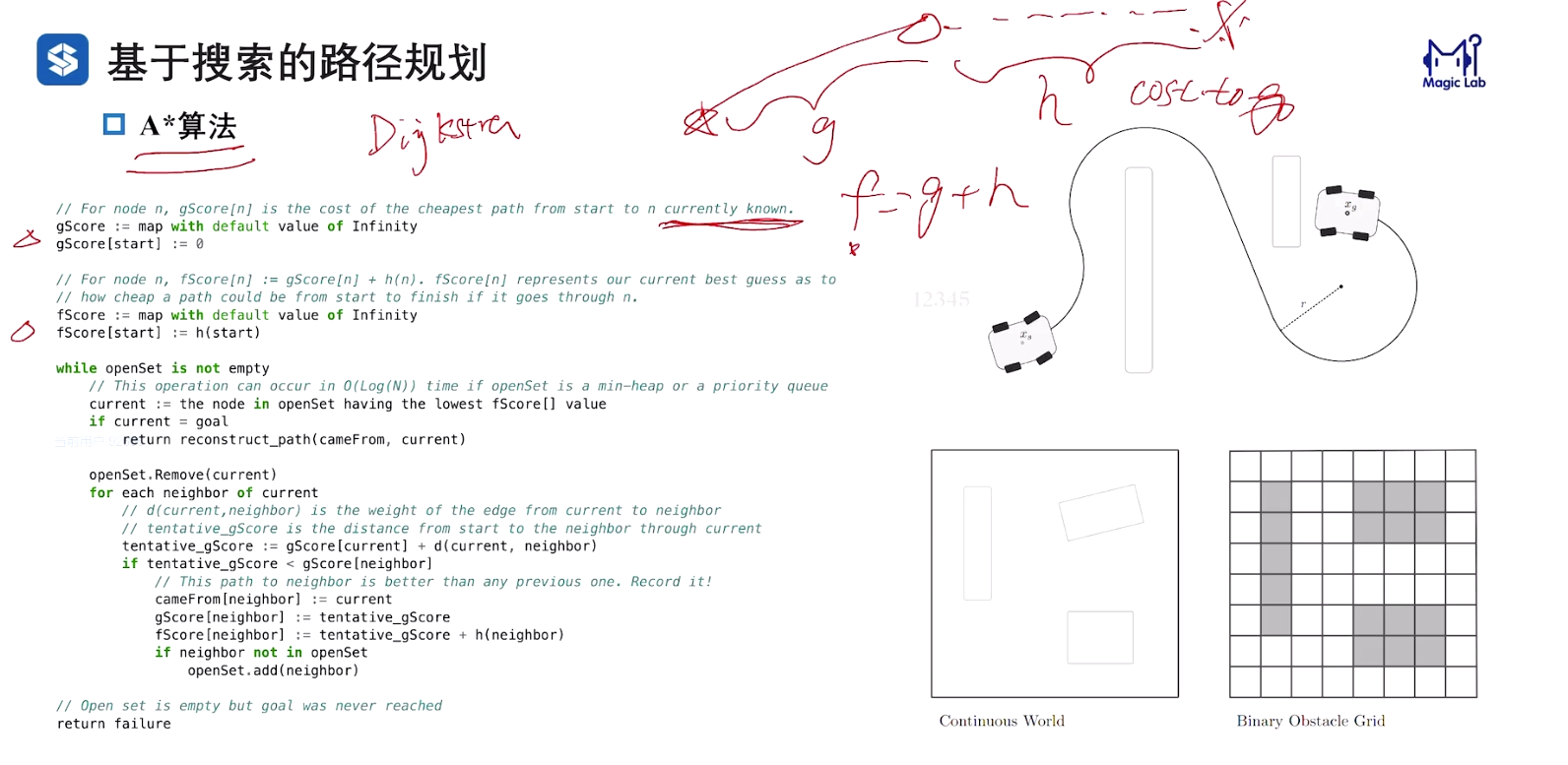
二维格点上进行 A* 算法缺点：不满足车辆的运动学约束

1.2 Hybrid A* 算法

Hybrid含义：

节点的拓展基于车辆运动学模型；
代价的计算基于栅格化地图；

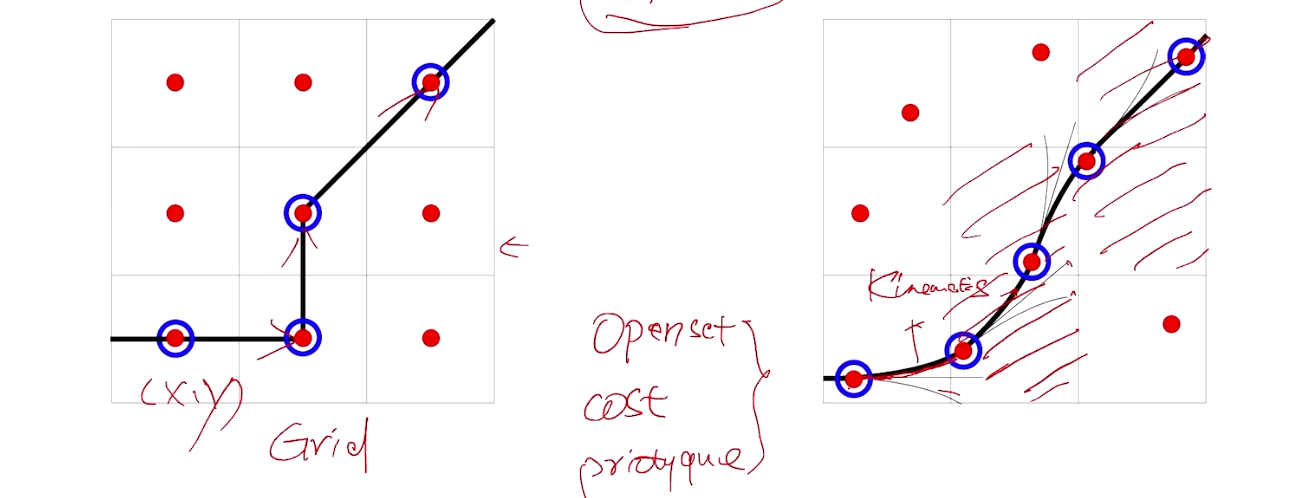
Hybrid A*算法的关键特性

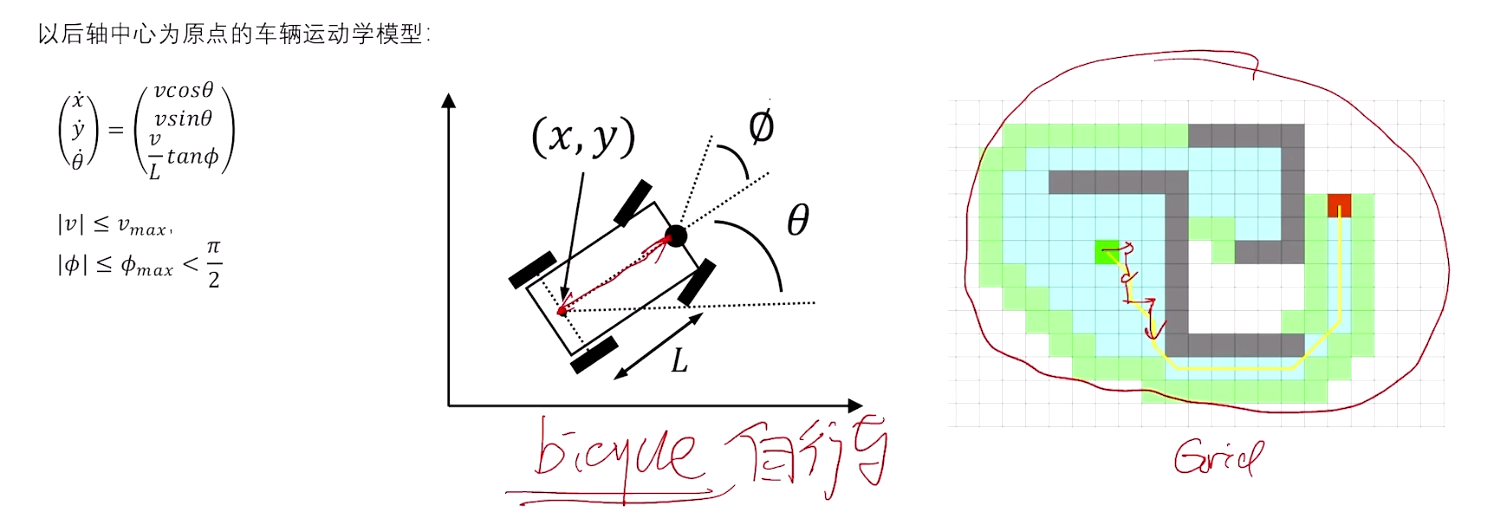
连续空间搜索:
- 传统A算法通常用于离散网格的搜索，例如二维网格上的路径规划。Hybrid A则在连续空间中进行搜索，允许路径规划的结果在更高的精度上表示车辆的位姿（位置和方向）。
- 车辆的状态不仅仅包括其在网格上的位置，还包括其方向和速度等动态信息。
车辆动力学约束:
- Hybrid A*考虑车辆的运动学和动力学约束，例如最小转弯半径、最大转向角等。这些约束使得路径规划的结果不仅是可达的，还必须是车辆能够实际执行的。
- 在搜索过程中，Hybrid A*会基于这些约束来生成平滑的轨迹，而不仅仅是直线或折线段。

Dubins 曲线：经典的圆弧直线法

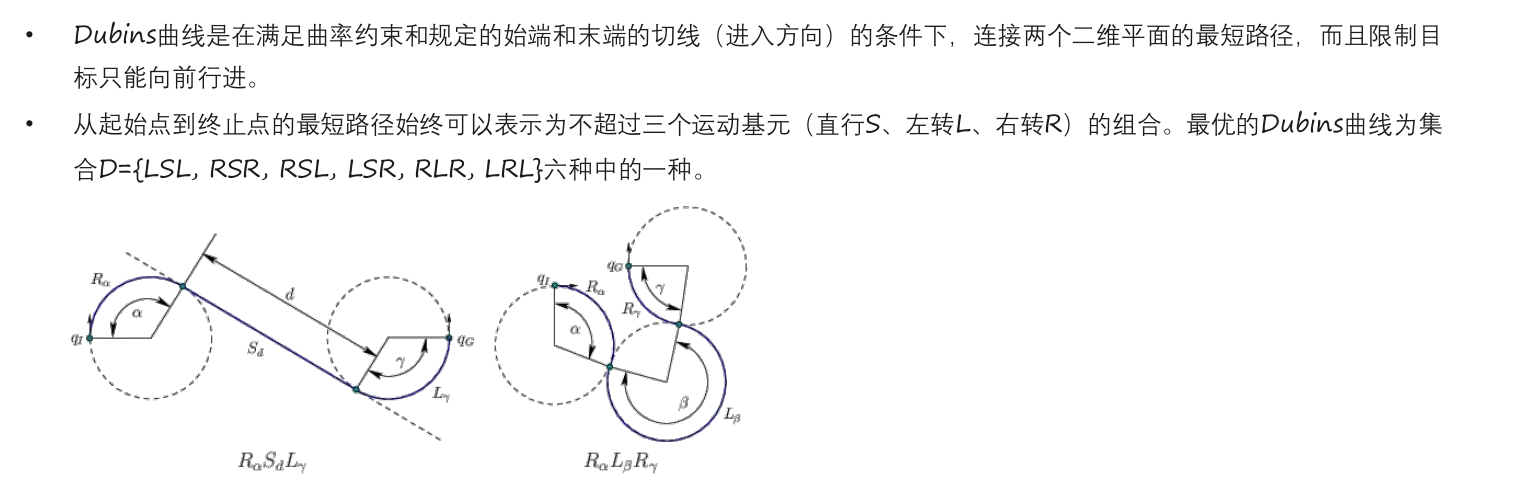
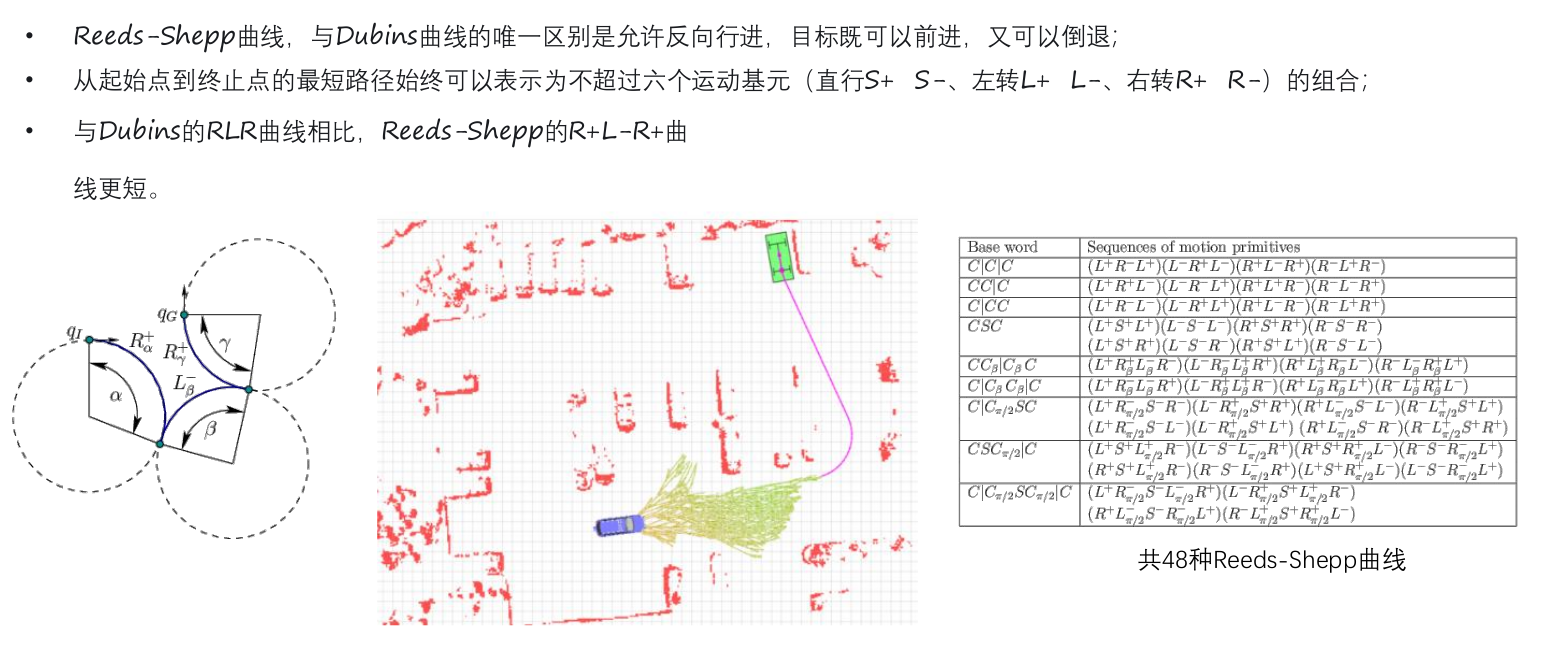
Reeds Shepp 曲线：可以倒车泊车主流算法。随着无图的自动驾驶，需要基于搜索，Hybrid A* 可以适用该场景。

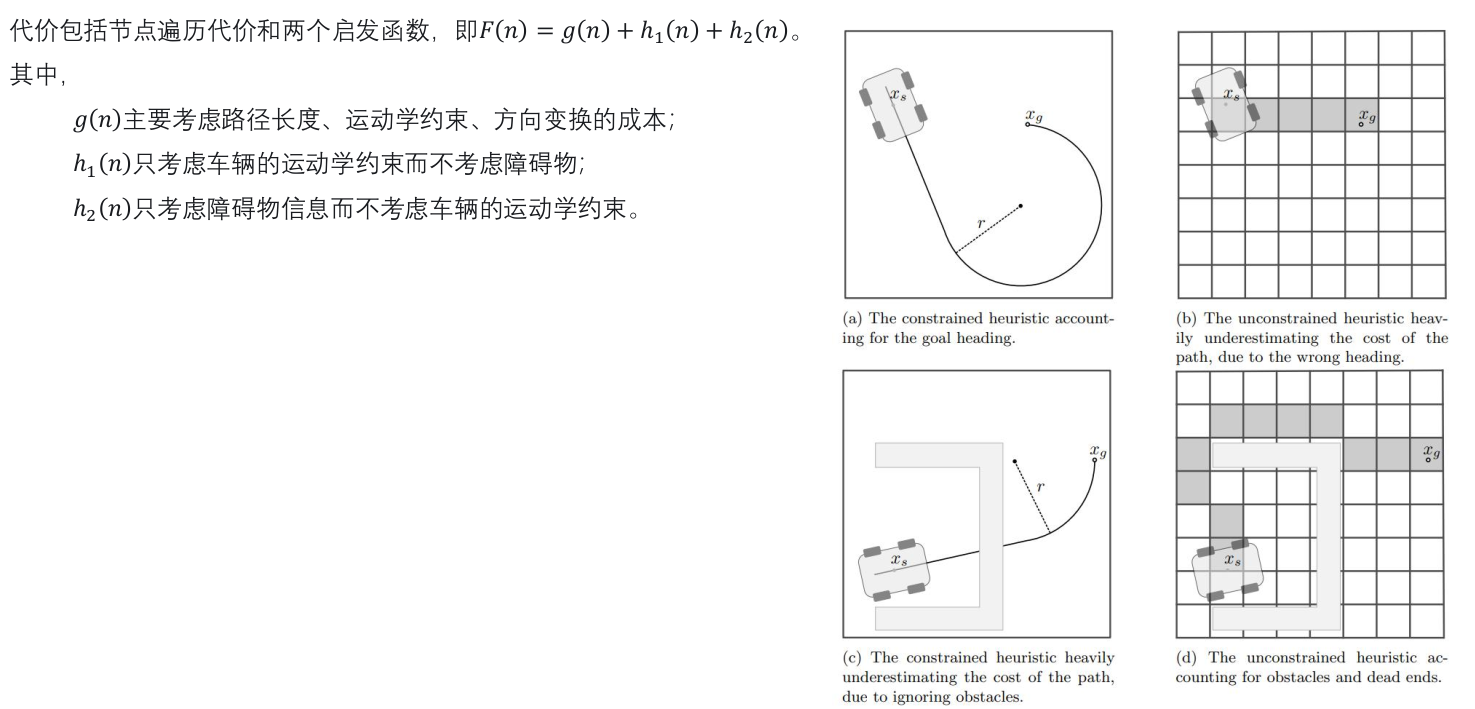
代价计算：

g(n): 路径长度、运动学约束、道路切合程度、方向突变、压实线、逆行等（过程代价，描述已知的代价）；

最短路径：

h1(n): 只考虑运动学约束，不考虑障碍物。

h2(n): 只考虑障碍物信息，通过格子去拓展，计算到终点的距离。基于经验，或者存图。

或者 leaning based huritical 。

伪代码流程：

2. 基于采样的路径规划

要求路径的一致性

2.1 Frenét Frame方法

缺点：很难约束极限道路场景下的曲率。（被参考线的曲率所欺骗）

Frenet坐标系是基于车辆的运动路径（通常称为参考路径）建立：

切向坐标 $s$ : 这是沿着参考路径的距离坐标。它表示在路径上某一点距离起点的弧长，也就是路径上的累计距离。
横向坐标 $l$ : 这是垂直于参考路径的距离坐标。它表示车辆当前位置偏离参考路径的横向距离，即从路径到车辆的最短距离。

2.2 Cartesian →Frenét 1D $(x, y)$ —> $(s, l)$

要将笛卡尔坐标系中的位置 $(x, y)$ 转换为 Frenet 坐标系中的 $(s, l)$ ，需要将车辆在参考路径上的位置进行投影，计算出对应的弧长 $(s)$ 和横向偏移 $(l)$ 。这个过程可以通过以下几个步骤来实现。

1. 计算 $(s)$ ：找到参考线上距离 $(x, y)$ 最近的投影点

方法 1：暴力遍历或二分查找（用于离散点形式的参考线）

暴力遍历：对参考线上的每个点计算到 (x, y) 的距离，选择距离最小的点作为投影点。

$d_i = \sqrt{(x - x_i)^2 + (y - y_i)^2}$

其中， $x_i, y_i) )$ 是参考线上的一个离散点。找到最小距离 $d_i )$ 所对应的点 $x_i, y_i)$ ，然后计算出该点对应的弧长 $(s)$ 。
二分查找：如果参考线是有序的，可以利用二分查找来加速寻找最近的点。

方法 2：梯度优化（用于多项式形式的参考线）

如果参考线由一个多项式表示，可以使用梯度下降法来找到 $(x, y)$ 到参考线的最短距离。设参考线方程为 $(y = f (x))$ ，则需要找到一个 $x^* )$ ，使得

$d(x^*) = \sqrt{(x - x^*)^2 + (y - f(x^*))^2}$

使 $d(x^*)$ 最小化。可以通过迭代的方法来求解这个优化问题，最终得到对应的 $x^*)$ 和 $y^* = f(x^*)$ 。

一旦找到最近点 $x^*, y^*)$ ，可以计算出对应的弧长 $(s)$ ，这通常可以通过数值积分计算，也可以根据预先计算的参考路径上的弧长来直接查表得到。

2. 计算 $(l)$ ：使用三角形向量关系

找到最近的投影点后，计算横向偏移 $(l)$ ：

向量定义：
- $\mathbf{r}(s)$ 是参考线上点 $(s)$ 处的坐标向量。
- $\mathbf{p}(x, y)$ 是车辆当前位置的坐标向量。
- $\mathbf{n}(s)$ 是参考线上 $(s)$ 处的法向量。
横向位移 $(l)$ 的计算：

通过向量的点积可以计算出横向位移 $(l)$ ：

$(\mathbf{p} - \mathbf{r}(s)) \cdot \mathbf{n}(s)$

其中， $\mathbf{n}(s)$ 是垂直于参考线在 $(s)$ 处的法向量。如果法向量朝向参考线左侧，那么 $(l)$ 为正，反之为负。

核心步骤总结

求 $(s)$ ：找到离车辆位置 $(x, y)$ 最近的参考线点，这可以通过暴力搜索或优化方法实现。
求 $(l)$ ：通过计算车辆位置和参考线投影点的法向量点积，求得横向偏移 $(l)$ 。

实际应用中的注意事项

参考线左侧、右侧方向不一致：需要注意法向量的方向。一般通过约定参考线法向量方向或使用方向向量进行修正，确保在 Frenet 坐标系中，左侧偏移为正，右侧偏移为负。
参考线的光滑性：如果参考线不是光滑的，则可能需要对参考线进行平滑处理，以确保计算结果的精度和稳定性。

求解S 代码：EPSILON/core/common/src/common/lane/lane.cc

ErrorType Lane::GetArcLengthByVecPosition(const Vecf<LaneDim>& vec_position,
                                          decimal_t* arc_length) // 寻找距离自车最近的点
ErrorType Lane::GetArcLengthByVecPositionWithInitialGuess( const Vecf<LaneDim>& vec_position, const decimal_t& initial_guess, decimal_t* arc_length） //牛顿法来近似计算曲线长度

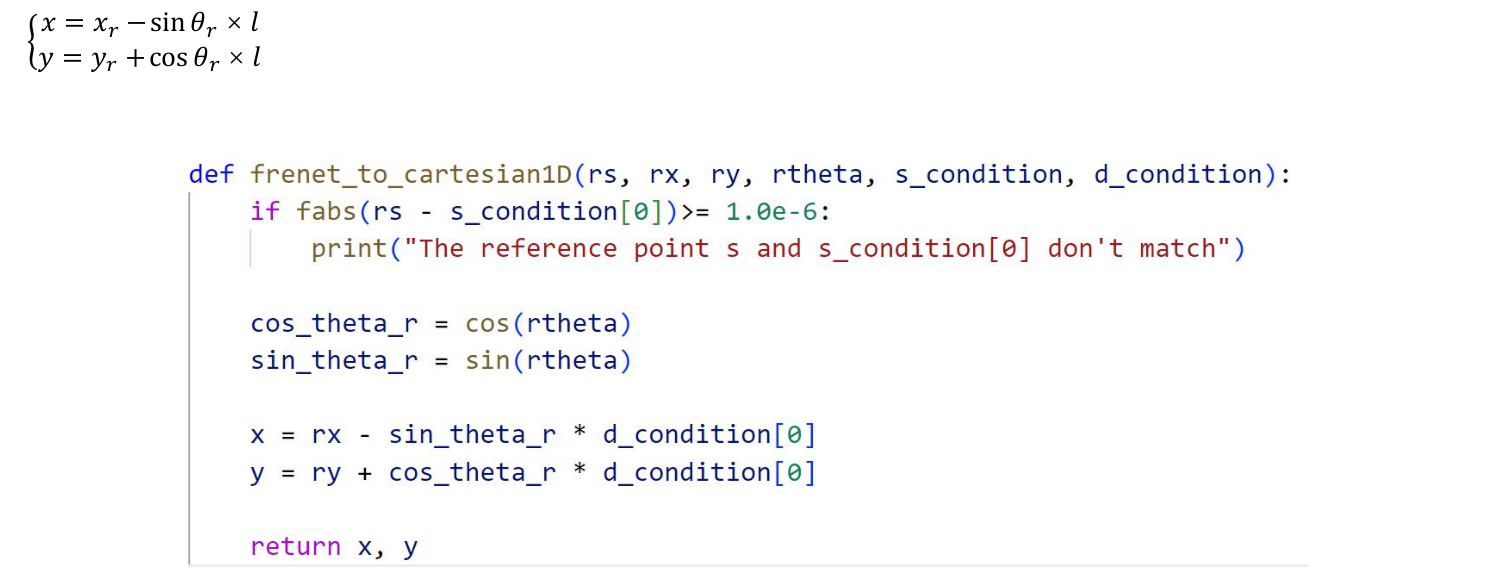
2.3 Cartesian →Frenét 3D

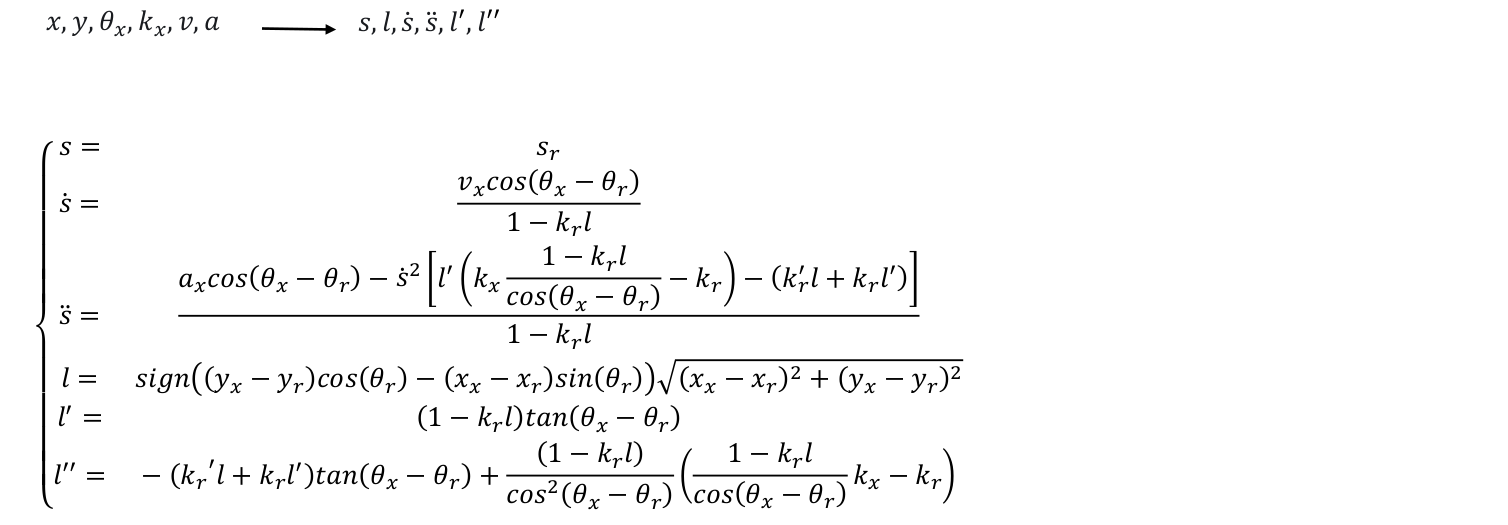
Frenét → Cartesian 3D

参考链接：
https://blog.csdn.net/qq_23981335/article/details/102832823
https://blog.csdn.net/AdamShan/article/details/80779615

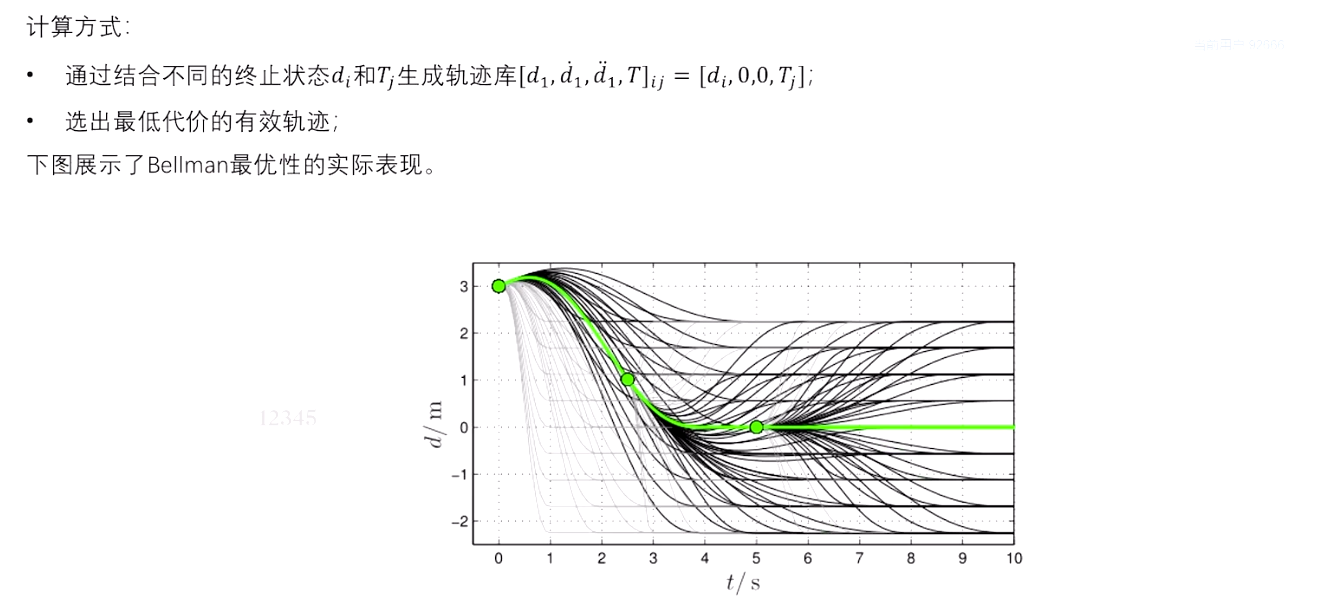
2.4 贝尔曼Bellman最优性原理

贝尔曼最优原理（Bellman’s Principle of Optimality）是动态规划（Dynamic Programming）中的核心思想之一。它是由美国数学家理查德·贝尔曼（Richard Bellman）提出的，用于解决多阶段决策问题。它的核心思想是，无论过程过去的状态和决策如何，对前面的决策所形成的状态而言，余下的决策必须构成最优策略。这个原理可以将一个复杂的问题分解为子问题，通过递归地解决这些子问题来找到最优解。

贝尔曼最优原理的定义

贝尔曼最优原理可以表述为：

一个问题的最优策略具备这样的性质：无论初始状态及初始决策如何，余下的决策必须构成最优策略，即从当前状态开始的决策序列是问题的最优解。

换句话说，假设一个问题可以分解为多个阶段，每个阶段的决策都会影响后续阶段的状态。贝尔曼最优原理指出，如果我们已经知道某个阶段之后的决策序列是最优的，那么在之前阶段的决策也必须是最优的，以确保整个决策序列是最优的。

形式化描述

假设我们有一个决策问题，它可以分为若干阶段。每个阶段的状态可以表示为 $(s)$ ，在每个状态 $(s)$ 下，可以选择一个决策 $(a)$ ，该决策会带来一个即时奖励 $(r (s, a)$ )，并将系统转移到下一个状态 $(s^{'})$ 。

令 $(V (s))$ 表示从状态 $(s)$ 开始并且遵循最优策略所能获得的最大期望收益。那么贝尔曼最优原理的递推公式（贝尔曼方程）可以表示为：

$\max_a \left[ r(s, a) + \gamma V(s') \right]$

其中：

$max_a )$ 表示在所有可能的行动 $(a)$ 中选择使得收益最大的那个行动。
$(r (s, a))$ 是在状态 $(s)$ 采取行动 $(a)$ 所获得的即时奖励。
$\gamma)$ 是折扣因子，用于表示未来收益的重要性。
$(s^{'})$ 是在状态 $(s)$ 采取行动 $(a)$ 后到达的下一个状态。

这个公式表示，从状态 $(s)$ 开始的最优价值 $(V (s))$ 是选择一个最优行动 $(a)$ ，使得当前的即时奖励和未来各阶段的最优价值（考虑到折扣因子）之和最大。

贝尔曼最优原理的优势

递归结构：贝尔曼方程提供了一个递归结构，允许我们通过逐步求解子问题来解决复杂的决策问题。
最优性保证：遵循贝尔曼最优原理的策略确保了最终解是全局最优的，而不是局部最优。

贝尔曼方程时间一致性
$k_t) = \max_{c_t} \left[ f(t, k_t, c_t) + V(t + 1, g(t, k_t, c_t)) \right]$
这里的 $V(t, k_t))$ 是在时间 $(t)$ 和状态 $k_t)$ 下的最优价值函数。方程表明，最优决策是在当前时间 $(t)$ 选择一个最优的控制 $KaTeX parse error: Can't use function '\)' in math mode at position 7: ( c_t \̲)̲$ ，使得当前的收益和下一步的最优价值之和最大。

轨迹的时间一致性：
在轨迹规划中，为了确保每一步规划的轨迹是连续且光滑的，需要遵循之前计算出的轨迹的剩余部分，确保时间一致性。
路径对比：
图中展示了两条不同时间步长下的轨迹规划（ $\Delta T_a )$ 和 ( $\Delta T_b )$ ）。这反映了在不同的时间尺度上，基于贝尔曼最优原理规划出的路径，如何在每个阶段选择最优的路径。

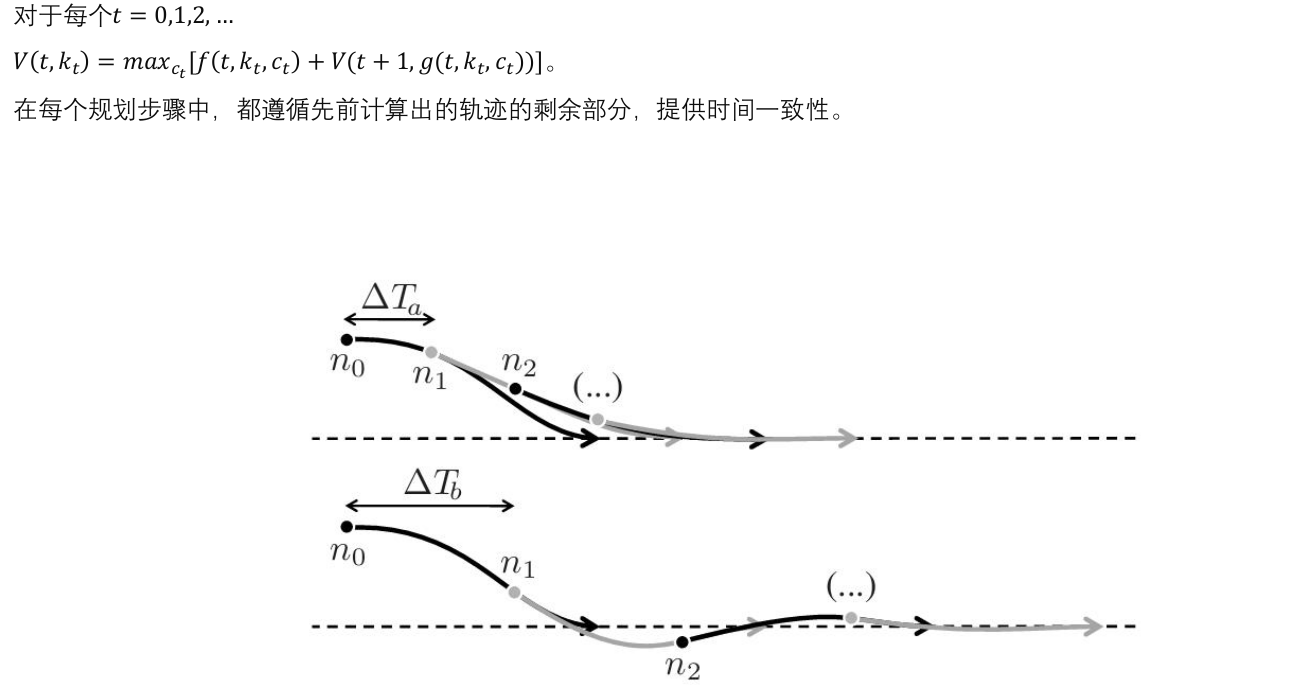
符合Bellman最优性 --> 解决最优控制问题

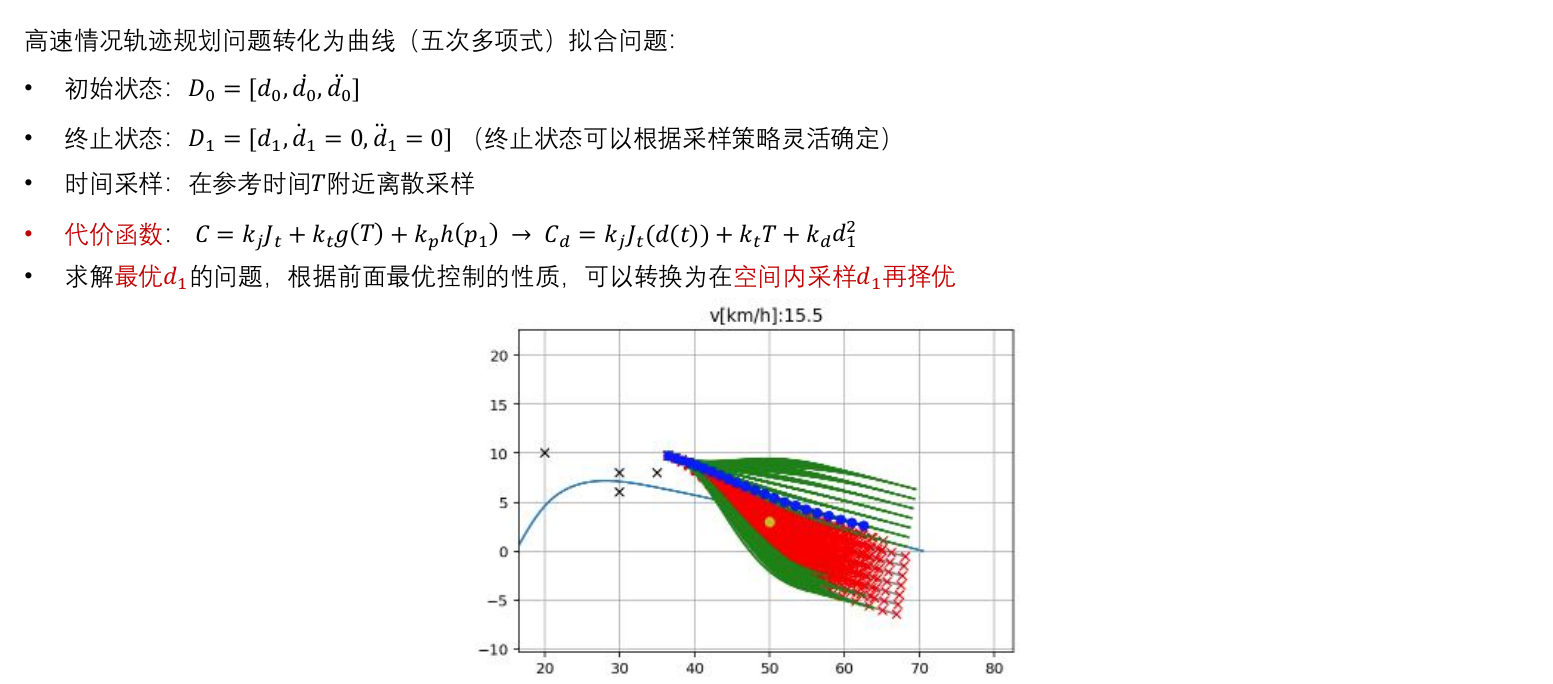
2.5 高速轨迹采样——横向

高速——横向运动相比于纵向运动相对幅度非常小，近似横纵向解耦，横纵向可独立计算。

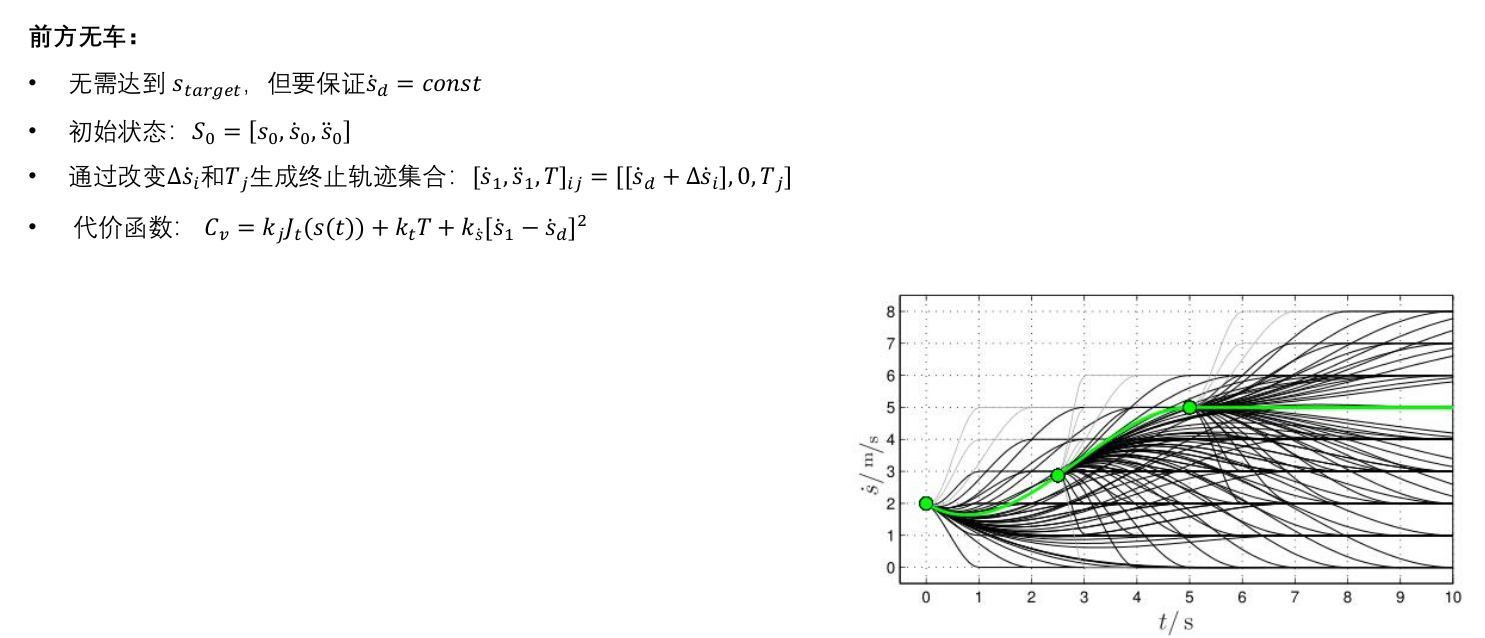
2.6 高速轨迹采样——纵向

2.7 低速轨迹规划——横向

低速——横向运动和纵向运动可比，而车辆有运动学约束，横纵向解耦会忽略运动学约束。

沿 S 采样。

横纵向采样轨迹结合以及代价评估

高速：横纵向解耦 $s (t) / d (t)$

低速：耦合 $s (t) d (s)$

如何确保曲率符合要求：大曲率要额外反投。高低速、大小曲率。

2.8 总结

整体流程：

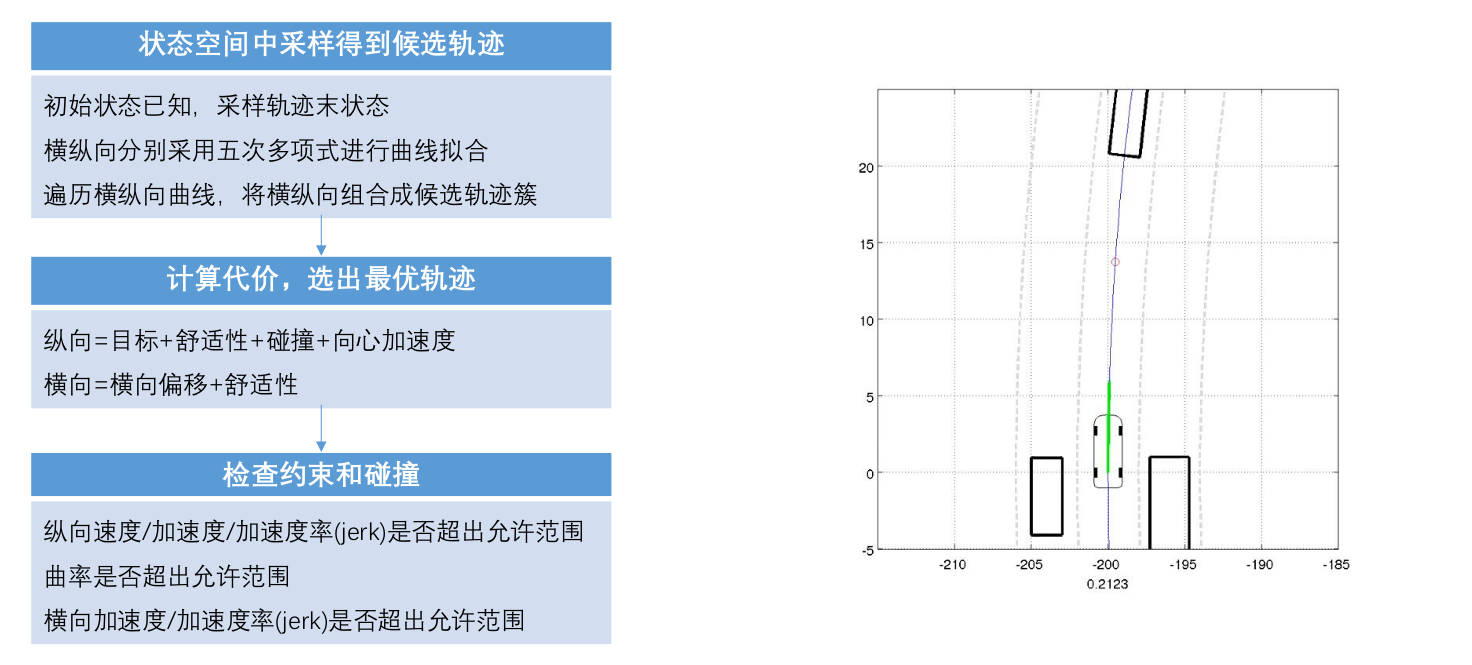
简单示例：

相关参考材料：

https://zhuanlan.zhihu.com/p/514864431
https://xueshu.baidu.com/usercenter/paper/show?paperid=14ec16ebb0e97cb89598c0aaef9f76d4&site=xueshu_se&hitarticle=1
https://blog.csdn.net/sinat_52032317/article/details/132924715?spm=1001.2101.3001.6650.1&utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7ERate-1-132924715-blog-118462640.235%5Ev43%5Epc_blog_bottom_relevance_base6&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7ERate-1-132924715-blog-118462640.235%5Ev43%5Epc_blog_bottom_relevance_base6&utm_relevant_index=2

3. 基于优化的路径规划

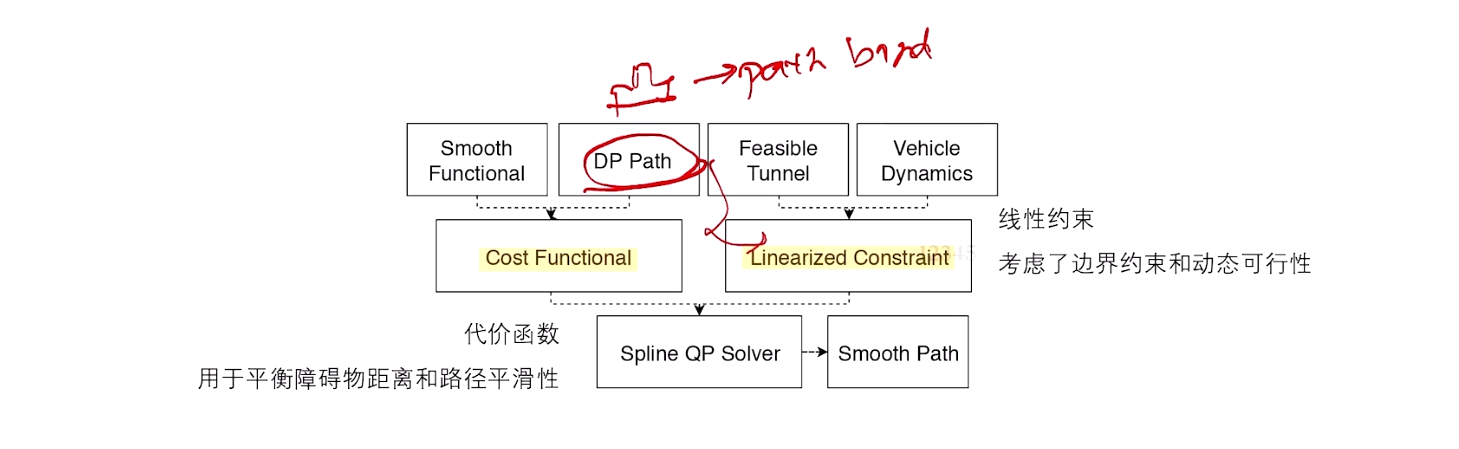
3.1 以百度Apollo EM planner为例

整体框架：

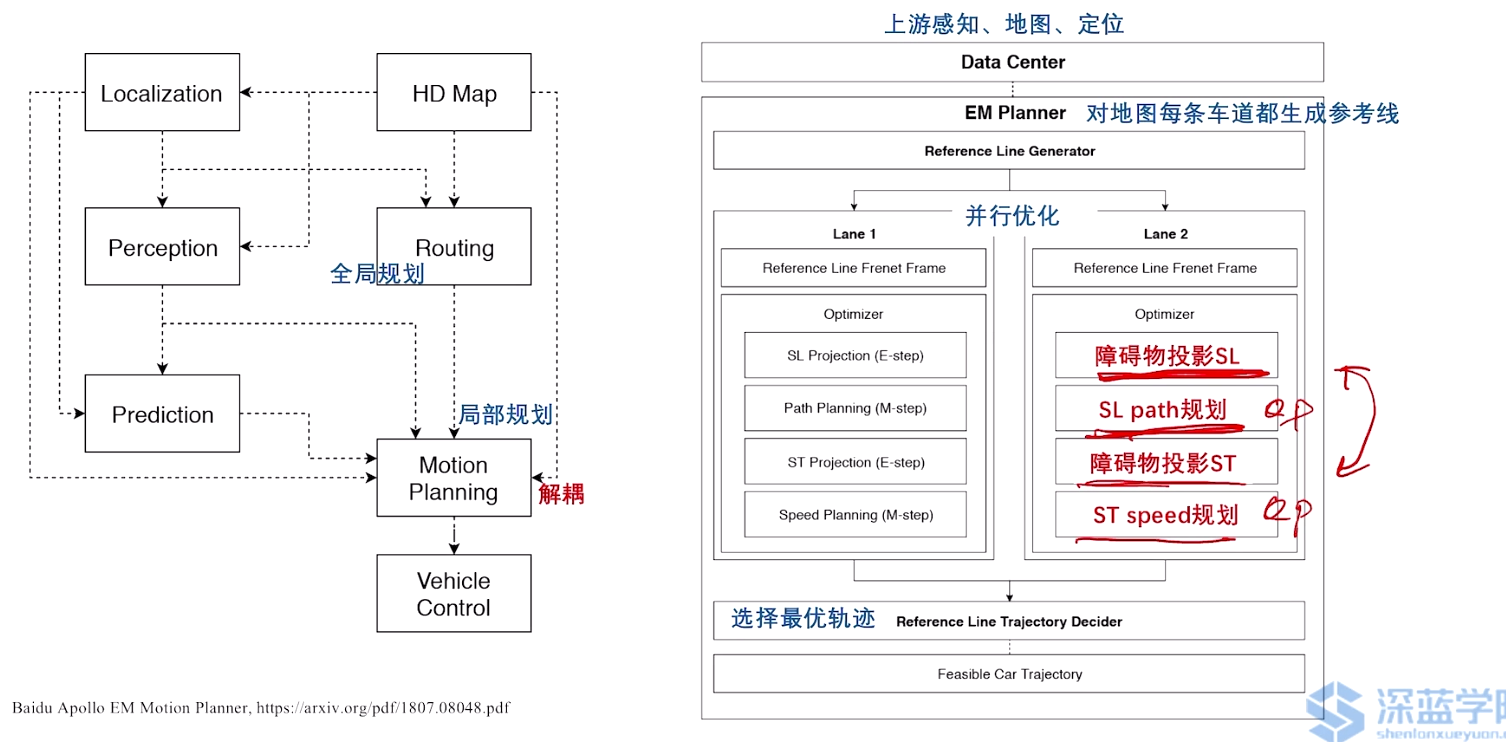
3.2 M-Step DP Path

路径：如何在 S L 坐标系下生成一条path，且满足一定的约束。

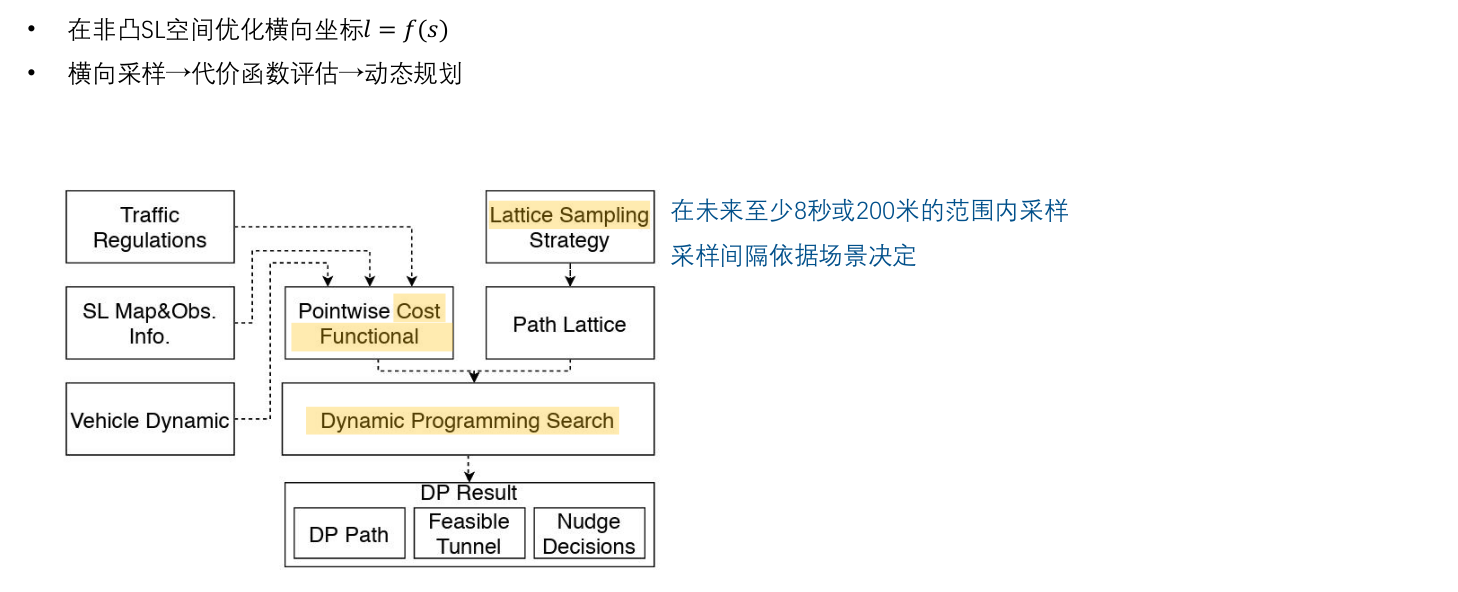
以向下绕行为例：

如果决策可以判断需要向下绕行 --> 可得到避障的上下界， Lower bound ≤ L(s) ≤ Upper bound --> Cost(f)

按照其他cost function 优化求解轨迹。

避障问题 --> 导致非凸 --> DP --> 初始解 --> QP 求解

避障问题 --> 如果可得到避障的上下界 --> 改为 cost function --> QP 求解

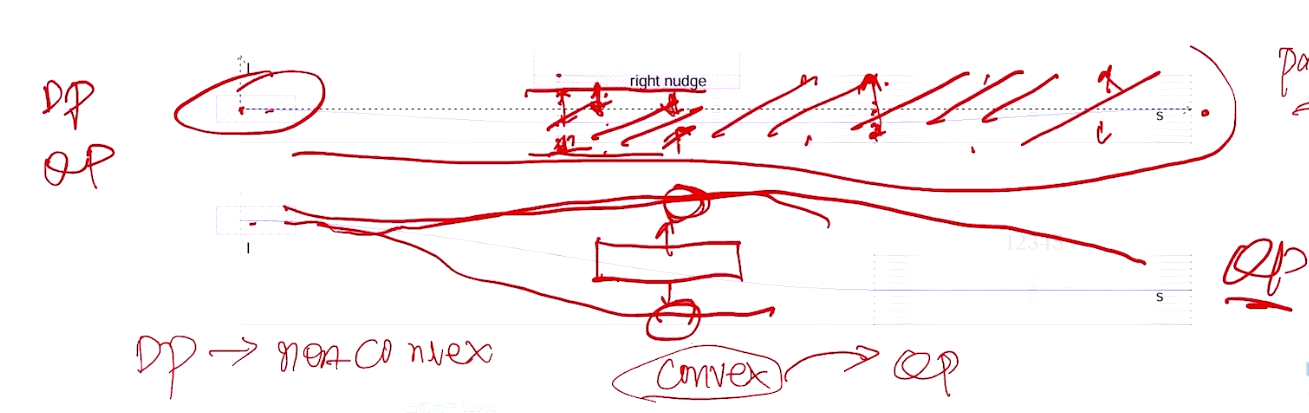
M-Step QP Path ——修正DP的path

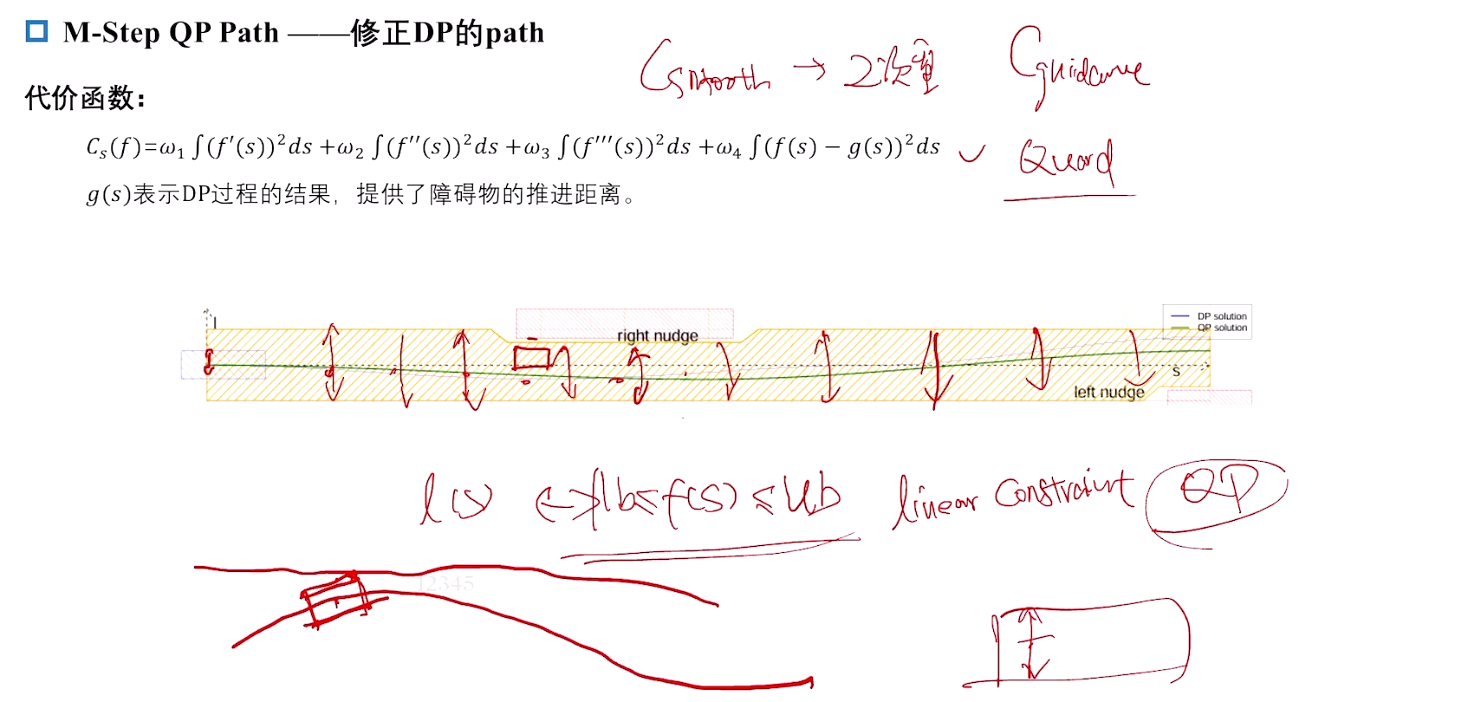
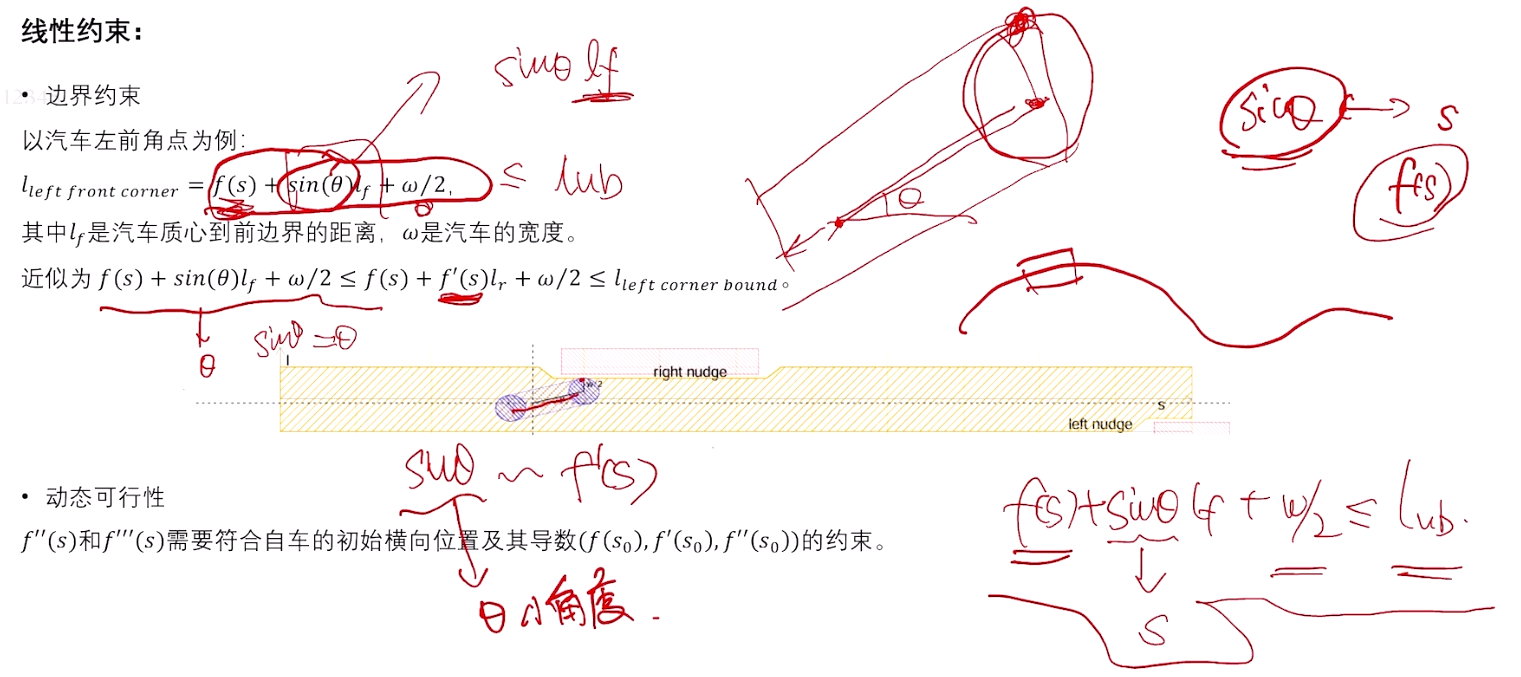
对自车碰撞处理，自车前角点做映射。当 $\theta$ 很小时，近似等于 $sin(\theta)$ ，再近似角度的抬高距离，f’(s)。

纵向非凸，可加速、减速。一般需要用DP搜索，克服非凸性。

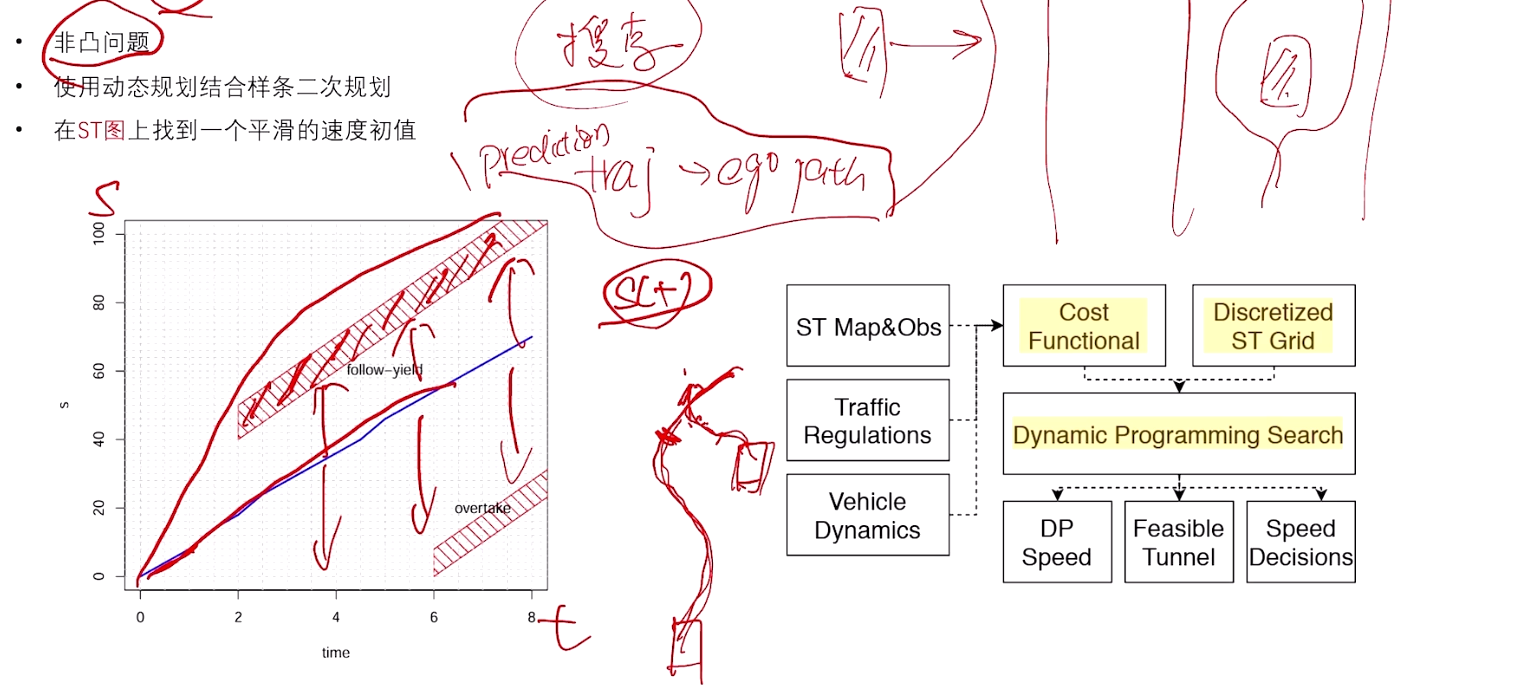
3.3 M-Step DP Speed Optimizerp

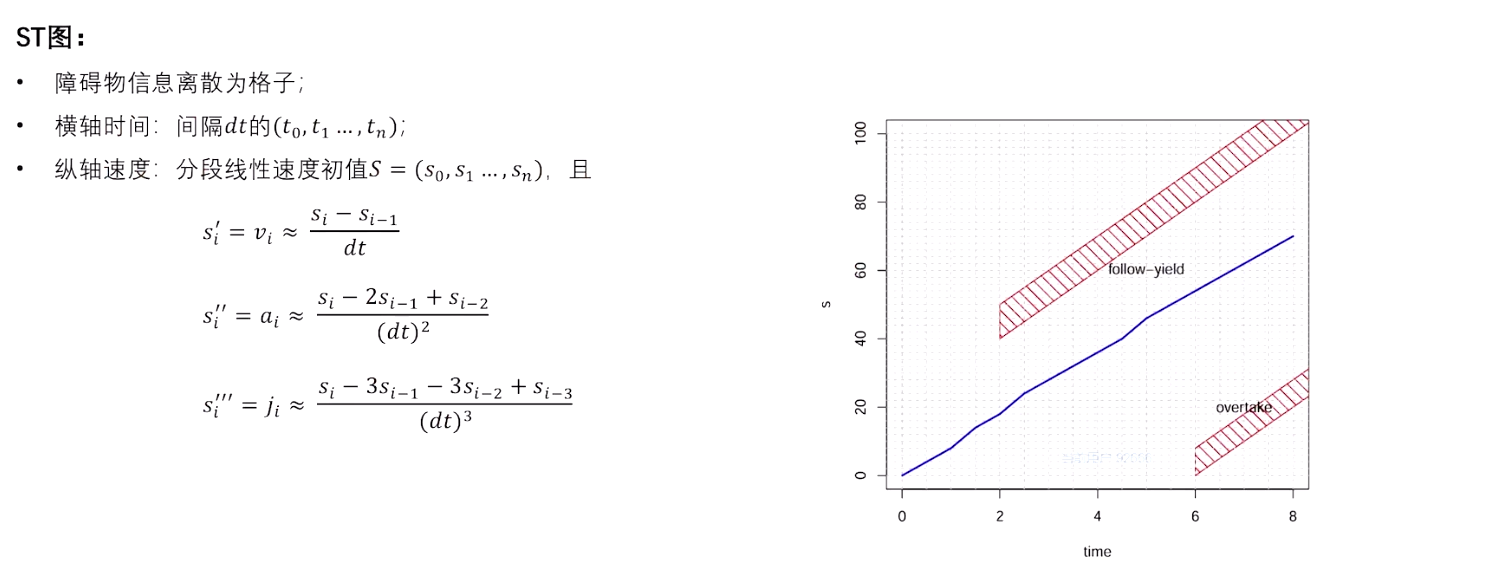
M-Step QP Speed Optimizer ——使得DP生成的分段线性速度初值满足动态要求

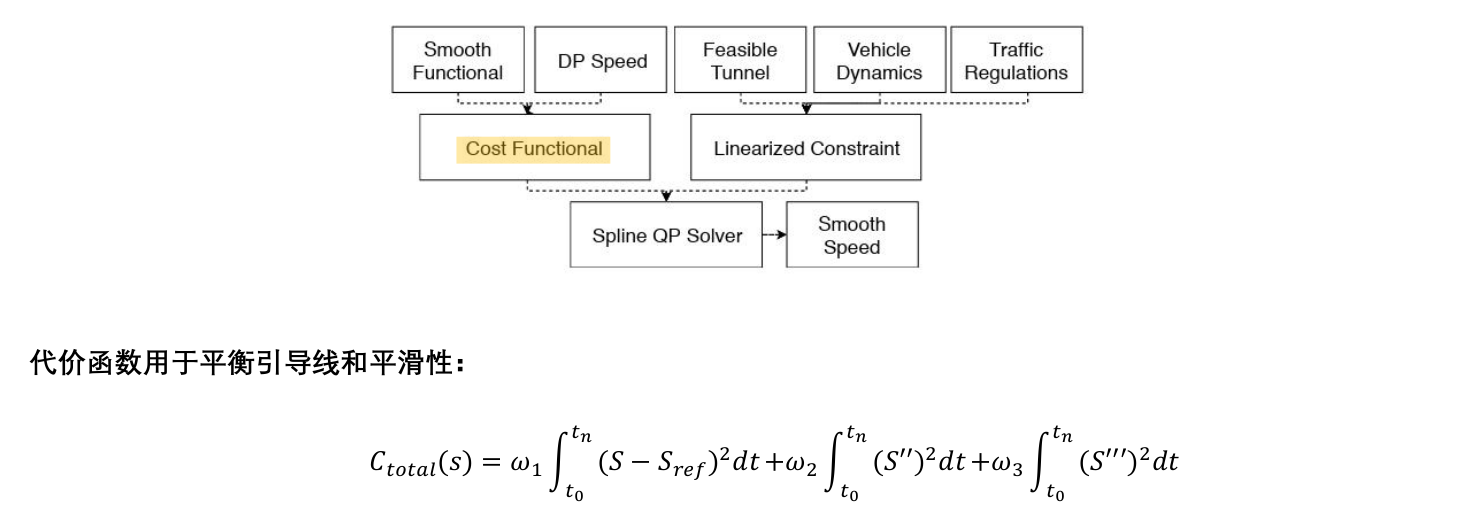
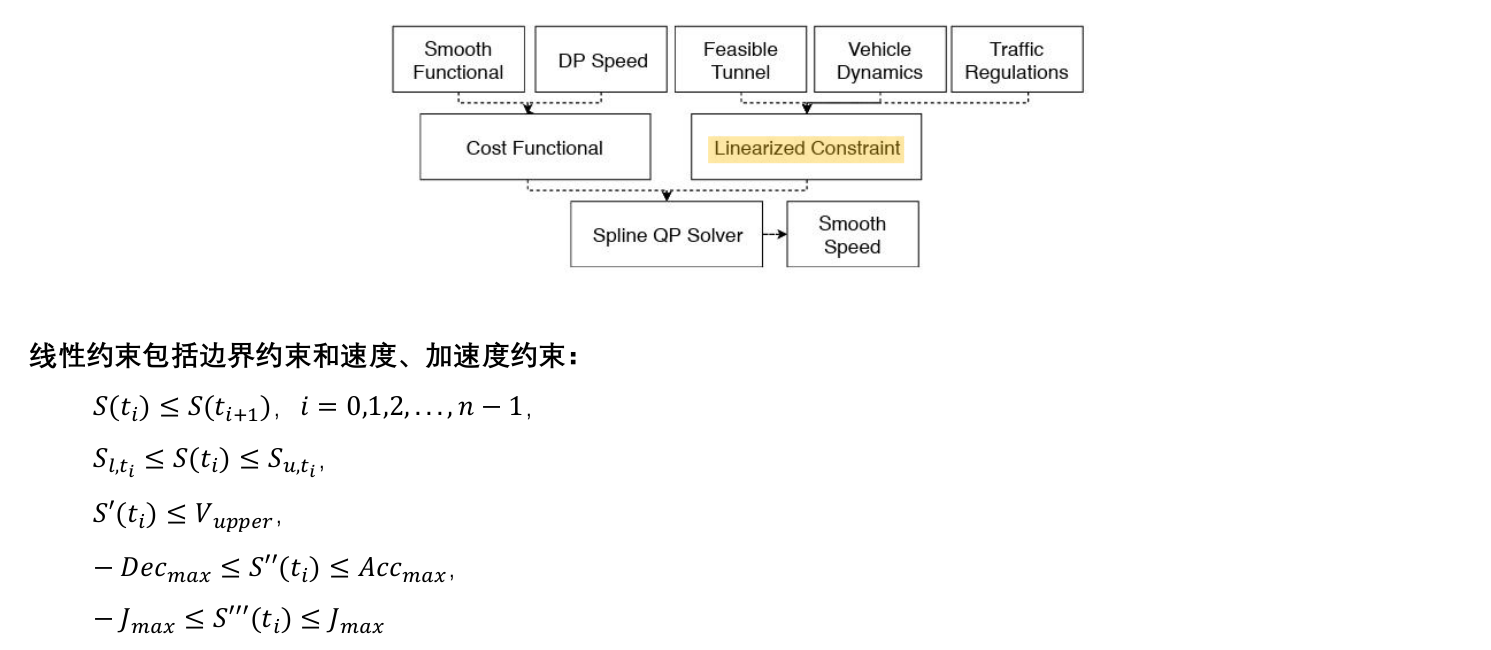
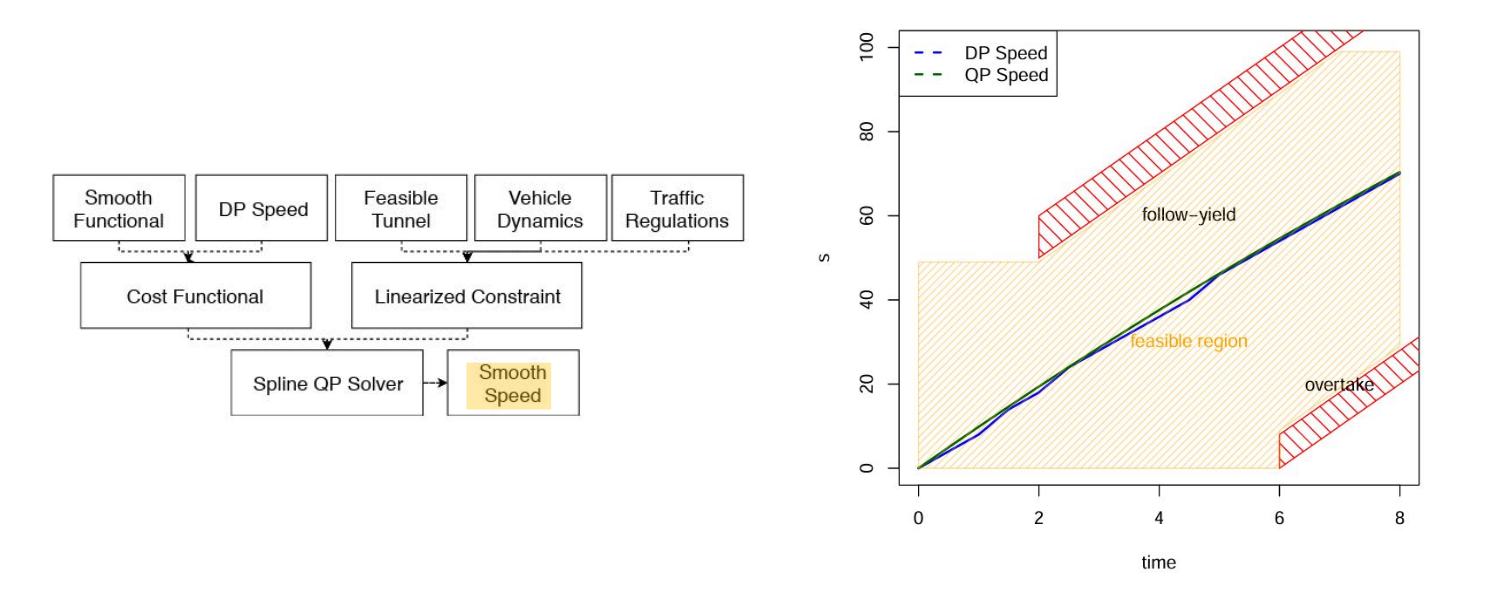
总结
DP+QP

DP：生成粗解和凸空间
QP：在凸空间求解
缺点：窄道会车场景

EM planner 参考：
https://arxiv.org/pdf/1807.08048.pdf
https://gitcode.com/ApolloAuto/apollo/tree/master/modules/planning?utm_source=csdn_github_accelerator&isLogin=1
https://blog.csdn.net/qq_39805362/article/details/128850317
https://blog.csdn.net/qq_41667348/article/details/125708616