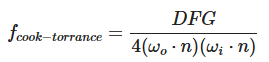1. PBR定义-基于物理的材质
PBR,或者用更通俗一些的称呼是指基于物理的渲染(Physically Based Rendering),它指的是一些在不同程度上都基于与现实世界的物理原理更相符的基本理论所构成的渲染技术的集合。
- 正因为基于物理的渲染目的便是为了使用一种更符合物理学规律的方式来模拟光线,因此这种渲染方式与我们原来的Phong或者Blinn-Phong光照算法相比总体上看起来要更真实一些。
- 除了看起来更好些以外,由于它与物理性质非常接近,因此我们(尤其是美术师们)可以直接以物理参数为依据来编写表面材质,而不必依靠粗劣的修改与调整来让光照效果看上去正常。
- 使用基于物理参数的方法来编写材质还有一个更大的好处,就是不论光照条件如何,这些材质看上去都会是正确的。
其中什么叫基于物理?也就是
- 基于物理的材质(Material)
- 基于物理的光源(Lighting)
- 基于物理适配的相机(Camera)
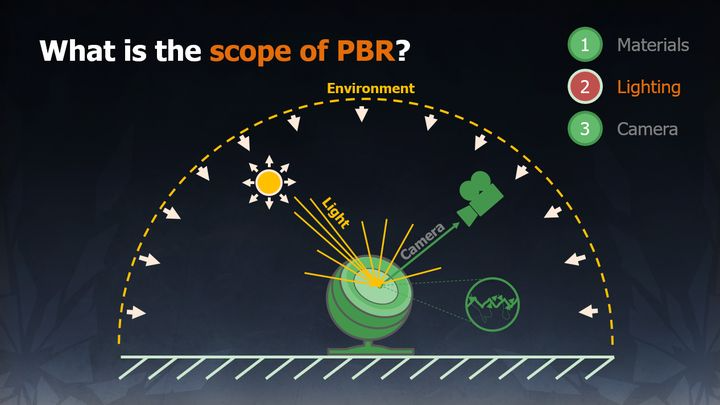
灯光相机也一样重要,但本节仅讲述基于物理的材质。
虽然如此,基于物理的渲染仍然只是对基于物理原理的现实世界的一种近似,这也就是为什么它被称为基于物理的着色(Physically based Shading) 而非物理着色(Physical Shading)的原因。判断一种PBR光照模型是否是基于物理的,必须满足以下三个条件:
- 基于微平面(Microfacet)的表面模型。
- 能量守恒。
- 应用基于物理的BRDF。
1.1. 微平面理论
所有的PBR技术都基于微平面理论。这项理论认为,达到微观尺度之后任何平面都可以用被称为微平面(Microfacets)的细小镜面来进行描绘。
镜面反射很好描述。
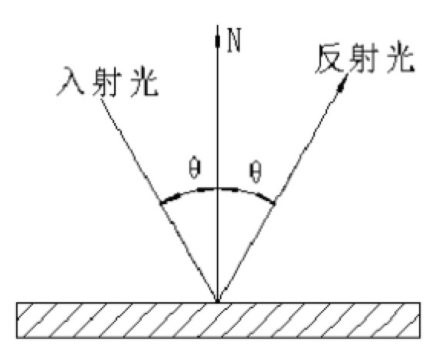
将复杂问题简单化,有了它就能很好的描述粗糙表面和光滑表面的区别。根据平面粗糙程度的不同,这些细小镜面的取向排列可以相当不一致。产生的效果就是:一个平面越是粗糙,这个平面上的微平面的排列就越混乱。这些微小镜面这样无序取向排列的影响就是,当我们特指镜面光/镜面反射时,入射光线更趋向于向完全不同的方向发散(Scatter)开来,进而产生出分布范围更广泛的镜面反射。而与之相反的是,对于一个光滑的平面,光线大体上会更趋向于向同一个方向反射,造成更小更锐利的反射:

在微观尺度下,没有任何平面是完全光滑的。然而由于这些微平面已经微小到无法逐像素地继续对其进行区分,因此我们假设一个粗糙度(Roughness)参数,然后用统计学的方法来估计微平面的粗糙程度。微平面的朝向方向与半程向量的方向越是一致,镜面反射的效果就越是强烈越是锐利。通过使用一个介于0到1之间的粗糙度参数,我们就能概略地估算微平面的取向情况了:

1.2. 能量守恒
微平面近似法使用了这样一种形式的能量守恒(Energy Conservation):出射光线的能量永远不能超过入射光线的能量(发光面除外)。如上图我们可以看到,随着粗糙度的上升,镜面反射区域会增加,但是镜面反射的亮度却会下降。如果每个像素的镜面反射强度都一样(不管反射轮廓的大小),那么粗糙的平面就会放射出过多的能量,而这样就违背了能量守恒定律。这也就是为什么正如我们看到的一样,光滑平面的镜面反射更强烈而粗糙平面的反射更昏暗。
为了遵守能量守恒定律,我们需要对漫反射光和镜面反射光做出明确的区分。当一束光线碰撞到一个表面的时候,它就会分离成一个折射部分和一个反射部分。反射部分就是会直接反射开而不进入平面的那部分光线,也就是我们所说的镜面光照。而折射部分就是余下的会进入表面并被吸收的那部分光线,也就是我们所说的漫反射光照。
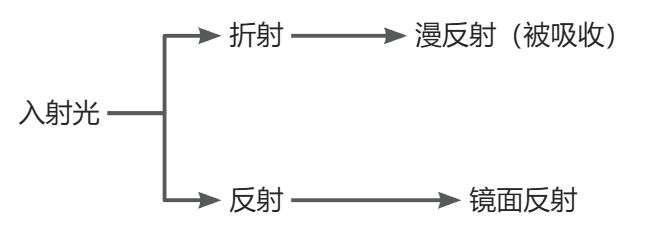
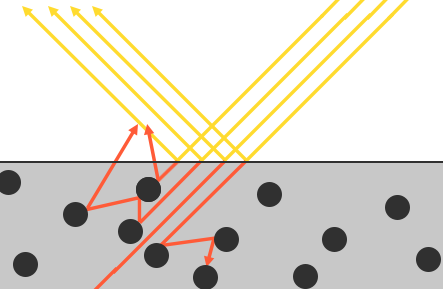
这里还有一些细节需要处理,因为当光线接触到一个表面的时候折射光是不会立即就被吸收的。通过物理学我们可以得知,光线实际上可以被认为是一束没有耗尽就不停向前运动的能量,而光束是通过碰撞的方式来消耗能量。每一种材料都是由无数微小的粒子所组成,这些粒子都能如下图所示一样与光线发生碰撞。这些粒子在每次的碰撞中都可以吸收光线所携带的一部分或者是全部的能量而后转变成为热量。
注意:
- 简化:一般来说,并非全部能量都会被吸收,而光线也会继续沿着随机的方向发散,然后再和其他的粒子碰撞直至能量完全耗尽或者再次离开这个表面。而光线脱离物体表面后将会协同构成该表面的(漫反射)颜色。不过在基于物理的渲染之中我们进行了简化,假设对平面上的每一点所有的折射光都会被完全吸收而不会散开。而有一些被称为次表面散射(Subsurface Scattering)技术的着色器技术将这个问题考虑了进去,它们显著地提升了一些诸如皮肤,大理石或者蜡质这样材质的视觉效果,不过代价是性能的下降。
- 金属:对于金属(Metallic)表面还有一个细节需要注意。金属表面对光的反应与非金属(也称为介电质(Dielectrics))相比是不同的。它们遵从的反射与折射原理是相同的,但是所有的折射光都会被直接吸收而不会散开,只留下镜面反射光。亦即是说,金属表面只会显示镜面反射颜色,而不会显示出漫反射颜色。由于金属与电介质之间存在这样明显的区别,因此它们两者在PBR渲染管线中被区别处理,而我们将在文章的后面进一步详细探讨这个问题。
- 互斥:反射光与折射光之间的这个区别使我们得到了另一条关于能量守恒的经验结论:反射光与折射光它们二者之间是互斥的关系。无论何种光线,其被材质表面所反射的能量将无法再被材质吸收。因此,诸如折射光这样的余下的进入表面之中的能量正好就是我们计算完反射之后余下的能量。
float kS = calculateSpecularComponent(...); // 反射/镜面 部分
float kD = 1.0 - ks; // 折射/漫反射 部分2. BRDF
2.1. 反射率方程
如何实现能量守恒?
- 使用反射率方程(Cook-Torrance反射方程)
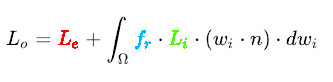

理解:
- 出射光=自发光+反射光
- 反射光=入射光*反射比例*入射衰减
- (入射光衰减:半角向量和法线的点积)
要正确地理解PBR,很重要的一点就是要首先透彻地理解反射率方程(这里假设没有自发光Le):
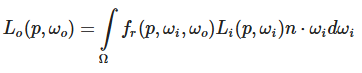
在渲染方程中L代表通过某个无限小的立体角ωi在某个点上的辐射率,而立体角可以视作是入射方向向量ωi。注意我们利用光线和平面间的入射角的余弦值cosθ来计算能量,也就是从辐射率公式L转化至反射率公式时的n⋅ωi=cosθ。用ωo表示观察方向,也就是出射方向,反射率公式计算了点p在ωo方向上被反射出来的辐射率Lo(p,ωo)的总和。或者换句话说:Lo表示了从ωo方向上观察,光线投射到点p上反射出来的辐照度。
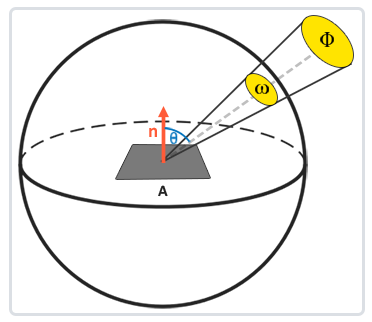
基于反射率公式是围绕所有入射辐射率的总和,也就是辐照度来计算的,所以我们需要计算的就不只是是单一的一个方向上的入射光,而是一个以点p为球心的半球领域Ω内所有方向上的入射光。一个半球领域(Hemisphere)可以描述为以平面法线n为轴所环绕的半个球体:
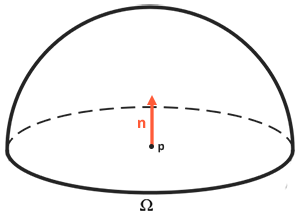
要用到积分∫运算包含了半球领域Ω内所有入射方向上的dωi 。在半球领域Ω中按一定的步长将反射率方程分散求解,然后再按照步长大小将所得到的结果平均化。
2.2. BRDF概念
现在唯一剩下的未知符号就是fr了
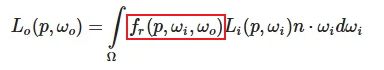
它被称为BRDF,或者双向反射分布函数(Bidirectional Reflective Distribution Function) ,它的作用是基于表面材质属性来对入射辐射率进行缩放或者加权。
![]()
。双向指的是相机方向和光源方向调换之后,他们的等级力量是一致的。
BRDF,或者说双向反射分布函数,它接受入射光方向ωi,出射/观察方向ωo,平面法线n以及一个用来表示微平面粗糙程度的参数a作为函数的输入参数。BRDF可以近似的求出每束光线对一个给定了材质属性的平面上最终反射出来的光线所作出的贡献程度。举例,如果一个平面拥有完全光滑的表面,那么只有一束与出射光线ωo拥有相同(被反射)角度的光线会返回1.0,其他所有的入射光线ωi的BRDF函数都会返回0.0 。
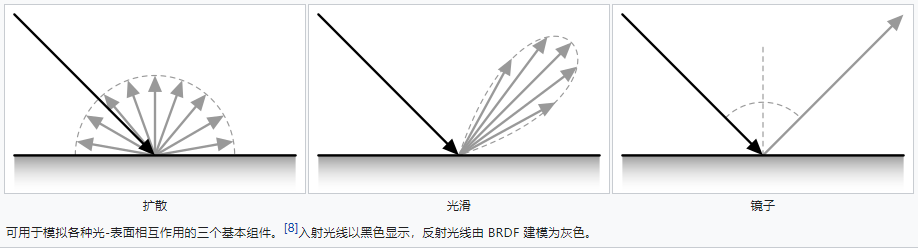
如下图的BRDF示意图,其中包含两部分
- BRDF:双向反射分布函数。光线入射后会散射和高光反射,其中散射在各个方向都是一样的
- BTDF:双向透射分布函数。包含散射和高光反射。
双向散射分布函数BSDF=BRDF+BTDF

因此只要知道入射光和反射光的方向,我们就可以知道反射比例。

2.3. BRDF的计算
BRDF是基于微平面理论和能量守恒定律的。严格上来说,同样采用ωi和ωo作为输入参数的 Blinn-Phong光照模型也被认为是一个BRDF。然而由于Blinn-Phong模型并没有遵循能量守恒定律,因此它不被认为是基于物理的渲染。现在已经有很好几种BRDF都能近似的得出物体表面对于光的反应,但是几乎所有实时渲染管线使用的都是一种被称为Cook-Torrance BRDF模型。
Cook-Torrance BRDF兼有两个部分:漫反射(扩散)和高光反射(光滑)(纯镜面反射很极端,考虑在高光反射中)
![]()

翻译:

2.3.1. 漫反射
漫反射的算法基本采用Lambert光照模型(经验模型),用如下的公式来表示:

c表示表面颜色,除以π是为了对漫反射光进行标准化,因为前面含有BRDF的积分方程是受π影响的。
光源方向与平面角度越垂直则反射强度越大,越平行则强度越小。即一束光横截面dA照射到平面上,dA不变,当α角度越大(越平行),照射到平面上的横截面的面积越大,因此单位光强变小。
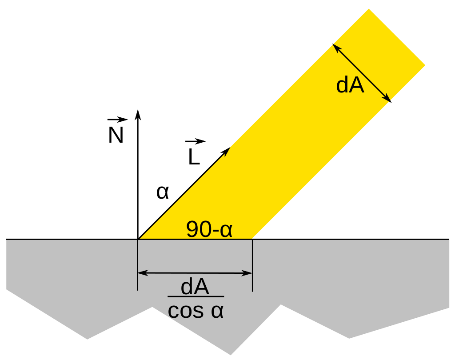
类似于地球接受太阳的光照
2.3.2. 基于物理的高光反射
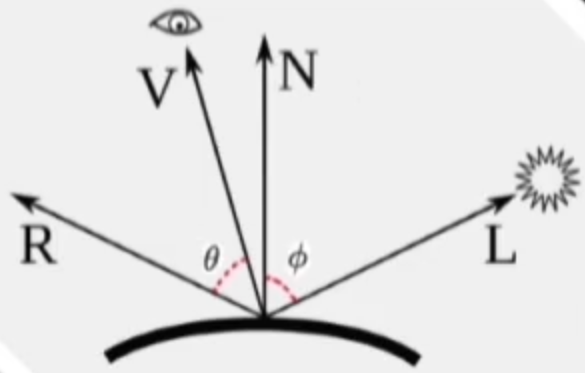
在以往的高光计算中使用Phong或Blinn-Phong光照模型是经验模型,不是基于物理的:
- Phong光照模型中
光线反射方向和视角方向夹角θ越大,高光反射强度越弱
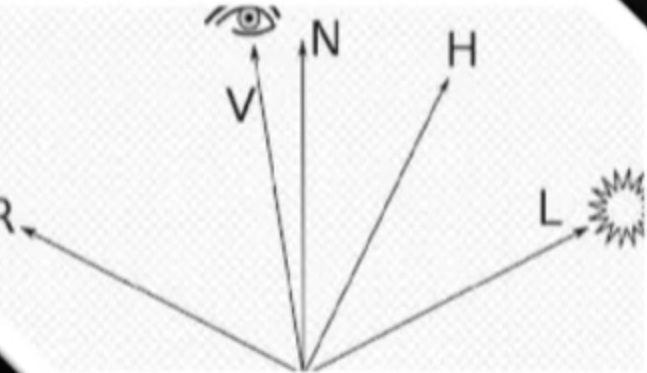
- Blinn-Phong光照模型中
半角方向和法线方向的夹角越大,高光反射强度越弱
我们需要的是PBR基于物理的渲染,因此我们不能继续使用经验模型作为BRDF项,需要引入基于物理的高光反射
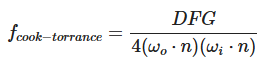
Cook-Torrance BRDF的镜面反射部分包含三个函数,此外分母部分还有一个标准化因子 。字母D,F与G分别代表着一种类型的函数,各个函数分别用来近似的计算出表面反射特性的一个特定部分。三个函数分别为:
- 法线分布函数(Normal Distribution Function):估算在受到表面粗糙度的影响下,朝向方向与半程向量一致的微平面的数量。这是用来估算微平面的主要函数。
- 几何函数(Fresnel Rquation):描述了微平面自成阴影的属性。当一个平面相对比较粗糙的时候,平面表面上的微平面有可能挡住其他的微平面从而减少表面所反射的光线。
- 菲涅尔方程(Geometry Function):菲涅尔方程描述的是在不同的表面角下表面所反射的光线所占的比率。
2.3.2.1. D-法线分布函数
法线分布函数D,从统计学上近似地表示了某些与半程向量h取向一致的微平面的比率,是用来描述法线对光衰减起作用的函数。举例来说,假设给定向量h,如果我们的微平面中有35%与向量h取向一致,则法线分布函数或者说NDF将会返回0.35。
目前有很多种NDF都可以从统计学上来估算微平面的总体取向度,只要给定一些粗糙度的参数。我们马上将要用到的是Trowbridge-Reitz GGX:
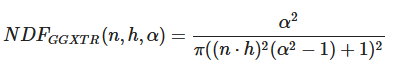
其中:
- α:粗糙度
- h:半角向量
- n:法线向量
之前的Blinn-Phong模型也描述了法线对光衰减的作用,但是他们之间是有区别的。下图可见GGX算法的结果在边缘更加狭长,外部更加发散,实验数据也证实了GGX的算法更符合真实情况。这部分主要是希望得到一个漂亮的高光效果。传统的Blinn-phong高光缺乏真实度,研究发现高光是带有拖尾的,例如铬金属的高光带有显著的拖尾,GGX模型就是为了把这个拖尾模拟出来,虽然还不能完全模拟,但是比之前的模型已经好了很多。

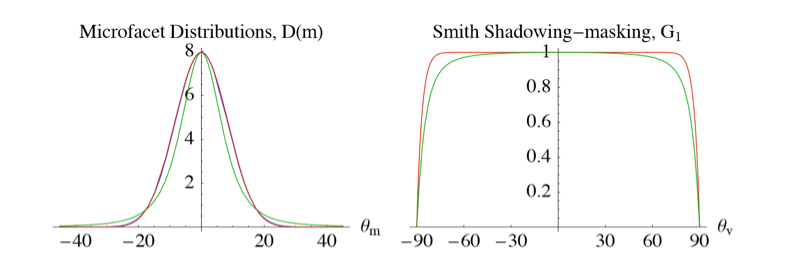
如果我们把h当成是不同粗糙度参数下的中间向量的话,我们可以得到如下图示的效果。当表面很光滑的时候,与半程向量取向一致的微平面会高度集中在一个很小的半径范围内。由于这种集中性,NDF最终会生成一个非常明亮的斑点。但是当表面比较粗糙的时候,微平面的取向方向会更加的随机。你将会发现与h向量取向一致的微平面分布在一个大得多的半径范围内,但是同时较低的集中性也会让我们的最终效果显得更加灰暗。

使用GLSL代码编写的Trowbridge-Reitz GGX法线分布函数是下面这个样子的:
float D_GGX_TR(vec3 N, vec3 H, float a)
{
float a2 = a*a;
float NdotH = max(dot(N, H), 0.0);
float NdotH2 = NdotH*NdotH;
float nom = a2;
float denom = (NdotH2 * (a2 - 1.0) + 1.0);
denom = PI * denom * denom;
return nom / denom;
}2.3.2.2. G-几何(遮蔽)函数
首先先知道我们使用的是微平面理论,即每个面单独计算互不干扰。但是在现实情况中,物体表面是存在凹凸相互遮蔽的情况的。例如下图光照射到凹陷处(几何阴影(Geometry Shadowing)),或者被平面遮挡(几何遮蔽(Geometry Obstruction)),不会反射到人眼。他们都会对光线造成衰减,而之前的计算这部分衰减没有表现出来。
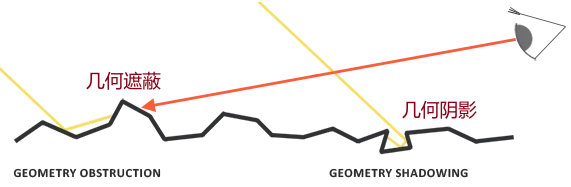
因此几何函数从统计学上近似的求得了微平面间相互遮蔽的比率;现在光线除了被吸收,还有被自身相互遮蔽带来的能量损耗。
与NDF类似,几何函数采用一个材料的粗糙度参数作为输入参数,粗糙度较高的表面其微平面间相互遮蔽的概率就越高。我们将要使用的几何函数是GGX与Schlick-Beckmann近似的结合体,因此又称为Schlick-GGX:
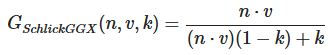
这里的k公式如下:

关于k的计算(roughness=α=1,k=1/2;roughness=α=1/4,k=1/8)因此k在1/2到1/8之间。当表面绝对光滑时也会吸收一部分光线,因此roughness=0时k不为0,毕竟完全不吸收光线的物体在现实中不存在。 平滑度roughness也会产生一定影响,大小在0-1之间,越粗糙roughness越大,α越接近1,遮蔽程度越大。
为了有效的估算几何部分,需要将观察方向(几何遮蔽)和光线方向向量(几何阴影)都考虑进去。我们可以使用史密斯法(Smith’s method)来把两者都纳入其中:
![]()
该式描述的是入射光方向l和视角方向v产生的光照衰减。之所以要乘两遍是因为光线在入射时会进行一次以光线方向l为参数的遮蔽,出射时会进行一次以视线方向v为参数的遮蔽,二者乘起来才是完整的G。
使用史密斯法与Schlick-GGX作为GsubGsub可以得到如下所示不同粗糙度的视觉效果:

几何函数是一个值域为[0.0, 1.0]的乘数,其中白色或者说1.0表示没有微平面阴影,而黑色或者说0.0则表示微平面彻底被遮蔽。
使用GLSL编写的几何函数代码如下:
float GeometrySchlickGGX(float NdotV, float k)
{
float nom = NdotV;
float denom = NdotV * (1.0 - k) + k;
return nom / denom;
}
float GeometrySmith(vec3 N, vec3 V, vec3 L, float k)
{
float NdotV = max(dot(N, V), 0.0);
float NdotL = max(dot(N, L), 0.0);
float ggx1 = GeometrySchlickGGX(NdotV, k);
float ggx2 = GeometrySchlickGGX(NdotL, k);
return ggx1 * ggx2;
}2.3.2.3. F-菲涅尔方程
被反射的光线对比光线被折射的部分所占的比率。通俗的说就是物体的边缘更亮一些,当垂直看物体时比在边缘角度看会暗很多。
菲涅尔方程是一个相当复杂的方程式,不过幸运的是菲涅尔方程可以用Fresnel-Schlick近似法求得近似解:
![]()
- h·v :为我们的高光项,视角越近高光越强,此处1-(h·v)取反,得到中间暗边缘亮;
- F0:表示平面的基础反射率,它是利用所谓折射指数(Indices of Refraction)或者说IOR计算得出的。然后正如你可以从球体表面看到的那样,我们越是朝球面掠角的方向上看(此时视线和表面法线的夹角接近90度)菲涅尔现象就越明显,反光就越强:
大多常见电介质的F0范围在[0.02-0.05],对于导体为[0.5-1.0]

-
菲涅尔方程还存在一些细微的问题。其中一个问题是Fresnel-Schlick近似仅仅对电介质或者说非金属表面有定义。对于导体(Conductor)表面(金属),使用它们的折射指数计算基础折射率并不能得出正确的结果,这样我们就需要使用一种不同的菲涅尔方程来对导体表面进行计算。由于这样很不方便,所以我们预计算出平面对于法向入射的结果(F0,处于0度角,好像直接看向表面一样),然后基于相应观察角的Fresnel-Schlick近似对这个值进行插值,用这种方法来进行进一步的估算。这样我们就能对金属和非金属材质使用同一个公式了。当我们在α角度看物体角度很小,反射就越多相应就更清晰。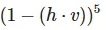

通过预先计算电介质与导体的F0值,我们可以对两种类型的表面使用相同的Fresnel-Schlick近似,但是如果是金属表面的话就需要对基础反射率添加色彩。对于大多数电介质表面而言使用0.04作为基础反射率可以在不需要输入额外表面参数的情况下得到物理可信的结果。然后,基于金属表面特性,我们要么使用电介质的基础反射率要么就使用F0来作为表面颜色。因为金属表面会吸收所有折射光线而没有漫反射,所以我们可以直接使用表面颜色纹理来作为它们的基础反射率。
vec3 F0 = vec3(0.04);
F0 = mix(F0, surfaceColor.rgb, metalness);Fresnel Schlick近似可以用代码表示为:
vec3 fresnelSchlick(float cosTheta, vec3 F0)
{
return F0 + (1.0 - F0) * pow(1.0 - cosTheta, 5.0);//cosTheta=表面法向量n与观察方向v的点乘
}注意:
也可以用:这样更快

有些地方的菲涅尔方程是这样的:一般不用
![]()
在这个方程里使用的是nv而不是vh。这nv和vh的冲突其实是宏观和微观的冲突。
使用nv的菲涅尔方程是宏观的,即菲涅尔方程确实由表面法线和视角方向求得。但在这里我们处理的不是宏观平面而是由法线分布函数D筛选出的法线为h的微平面,故这里实际用的应该是vh。也可以这么理解,微观上半角向量h就是微平面的法线,这也就是说Blinn-Phong光照模型本质上是一个BRDF。
3. 其他
3.1. Unity URP的BRDF
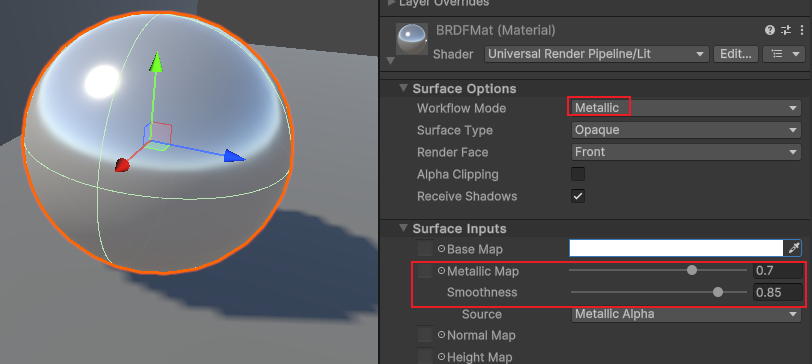
创建URP项目,材质中我们选择金属度工作流程URP/Lit

我们调节金属度反射Base Color的颜色,光滑度高反射环境光源;
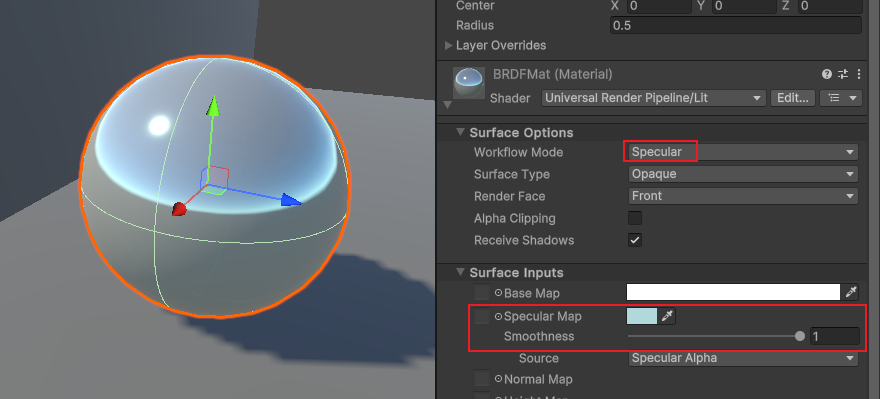
选择高光工作流程,金属度变为高光贴图即高光颜色设置。
我们进入URP Lit材质shader,第一个pass内看到的片元着色LitPassFragment并不在该shader中,下面显示#include "LitForwardPass.hlsl"。
// Shader Stages
#pragma vertex LitPassVertex
#pragma fragment LitPassFragment
...
#include "Packages/com.unity.render-pipelines.universal/Shaders/LitInput.hlsl"
#include "Packages/com.unity.render-pipelines.universal/Shaders/LitForwardPass.hlsl"我们进入该文件LitForwardPass.hlsl(Packages/com.unity.render-pipelines.universal/Shaders/LitForwardPass.hlsl),找到LitPassFragment函数,看到计算颜色的UniversalFragmentPBR函数。
#include "Packages/com.unity.render-pipelines.universal/ShaderLibrary/Lighting.hlsl"
void LitPassFragment(...)
{
...
half4 color = UniversalFragmentPBR(inputData, surfaceData);
...
}再打开Lighting.hlsl文件,找到这个UniversalFragmentPBR函数即为BRDF的片元计算。最后返回的color = GlobalIllumination(GI全局光照) + LightingPhysicallyBased(核心:基于物理的光照) + Emission(自发光)
half4 UniversalFragmentPBR(InputData inputData, SurfaceData surfaceData)
{
...
//环境光
lightingData.giColor = GlobalIllumination(...);
//基于物理的光照
lightingData.mainLightColor = LightingPhysicallyBased(...);
//返回光照
return CalculateFinalColor(lightingData, surfaceData.alpha);
}
half4 UniversalFragmentPBR(InputData inputData, half3 albedo, half metallic, half3 specular,
half smoothness, half occlusion, half3 emission, half alpha)
{
...
//自发光
surfaceData.emission = emission;
...
return UniversalFragmentPBR(inputData, surfaceData);
}
看Lighting.hlsl前面的基于物理的光照LightingPhysicallyBased函数
#include "Packages/com.unity.render-pipelines.universal/ShaderLibrary/BRDF.hlsl"
half3 LightingPhysicallyBased(...)
{
...
brdf += brdfData.specular * DirectBRDFSpecular(brdfData, normalWS, lightDirectionWS, viewDirectionWS);
}看BRDF.hlsl的DirectBRDFSpecular
// Computes the scalar specular term for Minimalist CookTorrance BRDF
half DirectBRDFSpecular(BRDFData brdfData, half3 normalWS, half3 lightDirectionWS, half3 viewDirectionWS)
{
...
// GGX Distribution multiplied by combined approximation of Visibility and Fresnel
// BRDFspec = (D * V * F) / 4.0
// D = roughness^2 / ( NoH^2 * (roughness^2 - 1) + 1 )^2
// V * F = 1.0 / ( LoH^2 * (roughness + 0.5) )
// See "Optimizing PBR for Mobile" from Siggraph 2015 moving mobile graphics course
// https://community.arm.com/events/1155
//法线分布函数NDF
// Final BRDFspec = roughness^2 / ( NoH^2 * (roughness^2 - 1) + 1 )^2 * (LoH^2 * (roughness + 0.5) * 4.0)
// We further optimize a few light invariant terms
// brdfData.normalizationTerm = (roughness + 0.5) * 4.0 rewritten as roughness * 4.0 + 2.0 to a fit a MAD.
float d = NoH * NoH * brdfData.roughness2MinusOne + 1.00001f;
half LoH2 = LoH * LoH;
half specularTerm = brdfData.roughness2 / ((d * d) * max(0.1h, LoH2) * brdfData.normalizationTerm);
specularTerm = clamp(specularTerm, 0.0, 1000.0); // Prevent FP16 overflow on mobiles
return specularTerm;
}
half3 DirectBDRF(BRDFData brdfData, half3 normalWS, half3 lightDirectionWS, half3 viewDirectionWS, bool specularHighlightsOff)
{
// Can still do compile-time optimisation.
// If no compile-time optimized, extra overhead if branch taken is around +2.5% on some untethered platforms, -10% if not taken.
[branch] if (!specularHighlightsOff)
{
half specularTerm = DirectBRDFSpecular(brdfData, normalWS, lightDirectionWS, viewDirectionWS);
half3 color = brdfData.diffuse + specularTerm * brdfData.specular;
return color;
}
else
return brdfData.diffuse;
}3.2. 迪士尼原则的BRDF
- 应使用直观的参数,而不是物理类的晦涩参数
- 参数应尽可能少
- 参数在其合理范围内应该为0到1
- 允许参数在有意义时超出正常的合理范围
- 所有参数组合应尽可能健壮和合理
用了11个参数即可非常真实地模拟出金属、非金属以及不同粗糙度的材质光照结果

4. 具体实现
4.1. 前提
- Edit>Project Setting>Player>Other Settings中将Color Space改成Linear
- Windows>Rendering>Lighting Setting>Scene最下面的Auto Generate关掉,如果已经有烘焙好的光照贴图就删掉。这一点主要是防止光照贴图对渲染效果产生影响。
- LUT设置
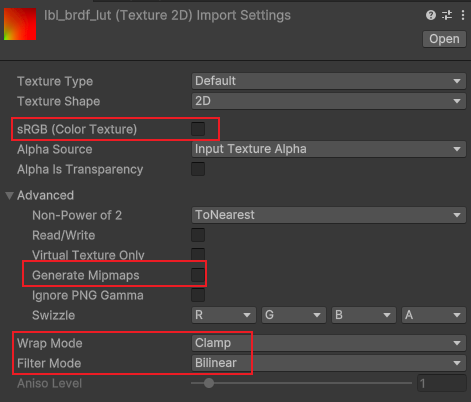
4.2. 思路
4.2.1. 直接光
漫反射
镜面反射
-
- D
-
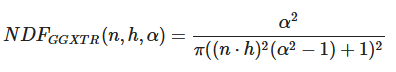
- G
-

- F
-

- or

4.2.2. 间接光

漫反射
镜面反射
-

-
(近似算法)

参考:
OpenGL:理论 - LearnOpenGL CN (learnopengl-cn.github.io)
毛星云PBR白皮书:GitHub - QianMo/PBR-White-Paper: ⚡️基于物理的渲染(PBR)白皮书 | White Paper of Physically Based Rendering(PBR)
unity build-in管线中的PBR材质Shader分析研究_bulit-in pbr-CSDN博客
从零开始在Unity中写一个PBR着色器:从零开始在Unity中写一个PBR着色器 - 简书