数据结构之树（下），你真的懂吗？

news2024/11/12 21:57:06

数据结构入门学习（全是干货）——树（下）

1 堆 (Heap)

1.1 什么是堆

堆 (Heap) 是一种特殊的完全二叉树，分为最大堆和最小堆。

  • 最大堆：每个节点的值都大于或等于其子节点的值，根节点是整个堆的最大值。
  • 最小堆：每个节点的值都小于或等于其子节点的值，根节点是整个堆的最小值。

堆常用来实现优先队列，支持高效的最大值/最小值查找、插入和删除操作。

优先队列(Priority Queue)：特殊的"队列"，取出元素的顺序是依照元素的优先权(关键字)大小，而不是元素进入队列的先后顺序

是否可以采用二叉树存储结构？
  • 二叉搜索树？ 堆不是二叉搜索树，虽然堆可以用二叉树的形式表示，但它并不满足二叉搜索树的“左小右大”性质。
二叉树结构对插入与删除的影响
  • 插入或删除时，堆的顺序如何安排？ 堆通常存储在数组中，插入或删除元素时必须保持二叉树的完全性，并且调整堆的结构以满足最大堆或最小堆的性质。
优先队列的完全二叉树表示

  • 堆通常用数组存储，每个节点的父节点和子节点的索引可以通过简单的数学运算确定：
    • 父节点：parent(i) = (i-1)/2
    • 左子节点：left(i) = 2*i + 1
    • 右子节点：right(i) = 2*i + 2
堆的抽象数据类型描述
  • 插入：Insert(x) 插入元素 x 到堆中，保持堆的有序性。
  • 删除：DeleteMax() 或 DeleteMin() 删除堆中最大或最小的元素，保持堆的有序性。

1.2 堆的插入

在最大堆中插入一个新元素时，必须保持最大堆的特性，即每个父节点的值必须大于等于其子节点的值。

最大堆的插入步骤：
  1. 将新元素插入到堆的末尾。
  2. 比较新元素与其父节点的值，如果新元素比父节点大，则交换两者的位置。
  3. 重复此过程，直到新元素的父节点不再比它小，或者新元素成为根节点。
插入算法：
void insert(MaxHeap *H, int value) {
    int i = ++H->size; // 将新元素插入堆的最后一个位置
    for (; i > 1 && value > H->Elements[i / 2]; i /= 2) {
        H->Elements[i] = H->Elements[i / 2]; // 向上移动父节点
    }
    H->Elements[i] = value; // 插入新元素
}
关键问题：
  • “哨兵”：在堆的创建过程中，常常会在堆的数组索引 0 处设置一个“哨兵”元素，用于简化插入和删除操作。通常哨兵的值设为一个极大值（如 MaxData），使得堆中的其他值都比它小。

1.3 堆的删除

在最大堆中，删除操作通常指的是删除堆的根节点，即堆中的最大值。

最大堆的删除步骤：
  1. 取出堆的根节点（最大值），同时将堆的最后一个节点移到根位置。

  1. 比较新根节点与其子节点的值，选择较大的子节点与根节点交换，保持堆的有序性。
  2. 重复此过程，直到根节点不再比子节点小，或节点成为叶子节点。
删除算法：
int deleteMax(MaxHeap *H) {
    int maxElement = H->Elements[1]; // 最大值
    int temp = H->Elements[H->size--]; // 用最后一个元素填补根
    int parent, child;

    for (parent = 1; parent * 2 <= H->size; parent = child) {
        child = parent * 2; // 左孩子
        if (child != H->size && H->Elements[child] < H->Elements[child + 1]) {
            child++; // 右孩子
        }
        if (temp >= H->Elements[child]) break; // 找到位置
        H->Elements[parent] = H->Elements[child]; // 向下移动
    }
    H->Elements[parent] = temp; // 插入最后的元素
    return maxElement; // 返回最大值
}

1.4 堆的建立

堆排序 是堆的一个常见应用，在堆排序中，我们首先需要将数组构建为一个堆。

最大堆的建立：

最大堆的建立可以通过下滤（Sift Down）方法，从堆中间位置开始，逐步调整每个子堆。

建立最大堆：将已经存在的N个元素按最大堆的要求存放在一个一维数组中

方法1：通过插入操作，将N个元素一个个相继插入到一个初始为空的堆中去，其时间代价最大为O(NlogN)
每次插入 它的时间复杂性是log2N
总共循环N遍，所以整个时间复杂性是Nlog2N
上方这个方法1的效率是不够的，我们可以有更好的方法
方法2：在线性时间复杂度下建立最大堆.
(1)将N个元素按输入顺序存入，先满足完全二叉树的结构特性
(2)调整各结点位置，以满足最大堆的有序特性
问题：

对于元素个数为12的堆，其各结点的高度之和是多少？答案是 10。

2 哈夫曼树与哈夫曼编码

2.1 什么是哈夫曼树

哈夫曼树（Huffman Tree） 又称为最优二叉树，是一种带权路径长度最短的树。带权路径长度（WPL）指的是所有叶子节点的权重乘以它们到根节点的路径长度之和。

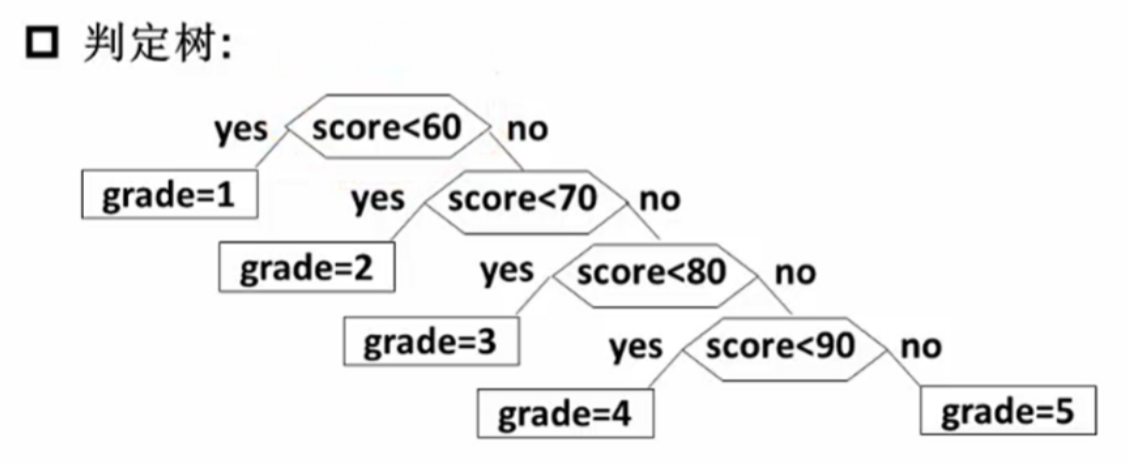
[例]将百分制的考试成绩转换成五分制的成绩

if(score < 60 ) grade = 1;
else if(score < 70) grade = 2;
else if(score < 80) grade = 3;
else if(score < 90) grade = 4;
else grade = 5;

上述代码中，其实对应着就有一棵树，如下图：

优化后的效率：

if(score < 80)
{
    if(score < 70 )
        if(score < 60) grade = 1;
    else grade = 2;
}else if(score < 90 )grade = 4;
else grade = 5;
哈夫曼树的性质：
  • 哈夫曼树是带权路径长度最小的二叉树。
  • 没有度为1的节点。
  • 如果有 n 个叶子节点，则哈夫曼树有 2n - 1 个节点。
举例：

有5个叶子节点，它们的权值为 {1，2，3，4，5}。根据这些权值可以构造多个不同的二叉树，但哈夫曼树保证了最小的带权路径长度。

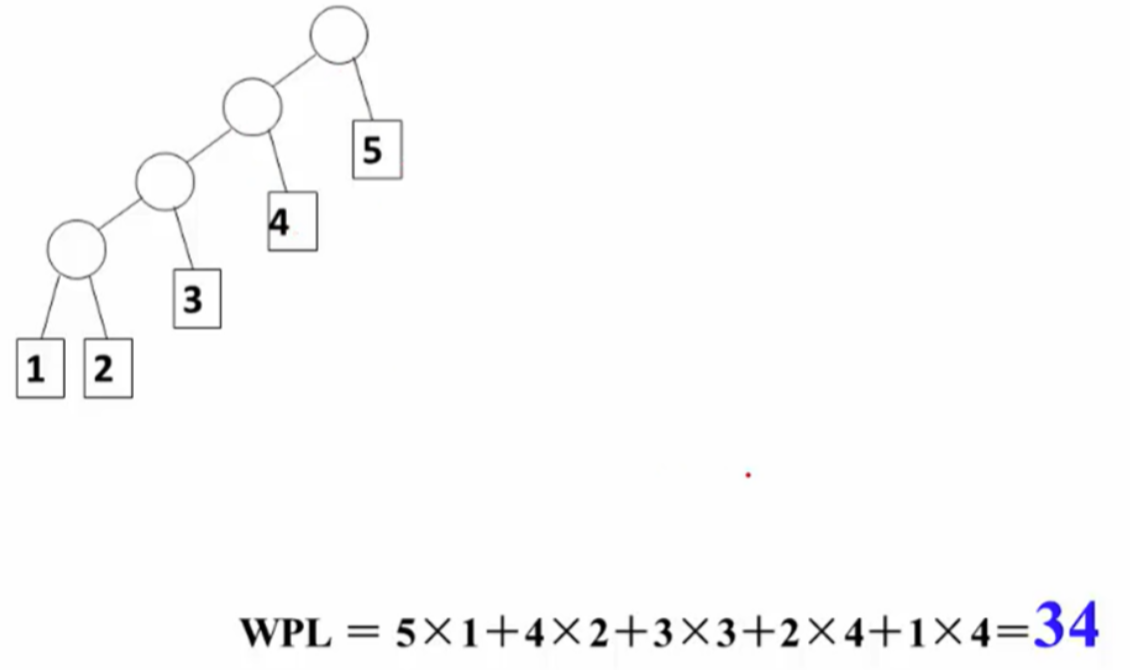
是50

2.2 哈夫曼树的构造

哈夫曼树的构造方法：

  1. 将所有节点看作一个森林，每棵树仅有一个节点，权重为该节点的权值。
  2. 每次选取权值最小的两棵树，合并成一棵新的树，新树的权值为两棵树的权值之和。
  3. 重复上述过程，直到所有节点被合并成一棵树。
typedef struct TreeNode *HuffmanTree;
struct TreeNode{
    int Weight;
    HuffmanTree Left,Right;
}
HuffmanTree Huffman(MinHeap H)
{
    //假设H->Size个权值已经存在H->Elements[]->Weight里
    int i; HuffmanTree T;
    BuildMinHeap(H);//将H->Elements[]按权值调整为最小堆
    for(i = 1;i < H->Size; i++){//做H->Size-1次合并
        T = malloc(sizeof(struct TreeNode));//建立新结点
        T->Left = DeleteMin(H);//从最小堆中删除一个结点，作为新T的左子结点
        T->Right = DeleteMin(H);//从最小堆中删除一个结点，作为新T的右子结点
        T->Weight = T->Left->Weight+T->Right->Weight;//计算新权值
        Insert(H,T);//将新T插入最小堆
    }
    T = DeleteMin(H);
    return T;
}
整体复杂度为O(NlogN)
哈夫曼树的特点：
  1. 没有度为1的节点。
  2. 任意非叶子节点的左右子树交换后仍是哈夫曼树。
  3. n 个叶子节点的哈夫曼树共有 2n - 1 个节点。

2.3 哈夫曼编码

哈夫曼编码是一种前缀编码法，用于对字符进行不等长编码，使得高频字符的编码较短，低频字符的编码较长，从而减少总的编码长度。

哈夫曼编码的步骤：
  1. 根据字符出现的频率构造哈夫曼树。
  2. 从根节点到叶子节点的路径表示字符的编码。向左分支为 0，向右分支为 1。
举例：

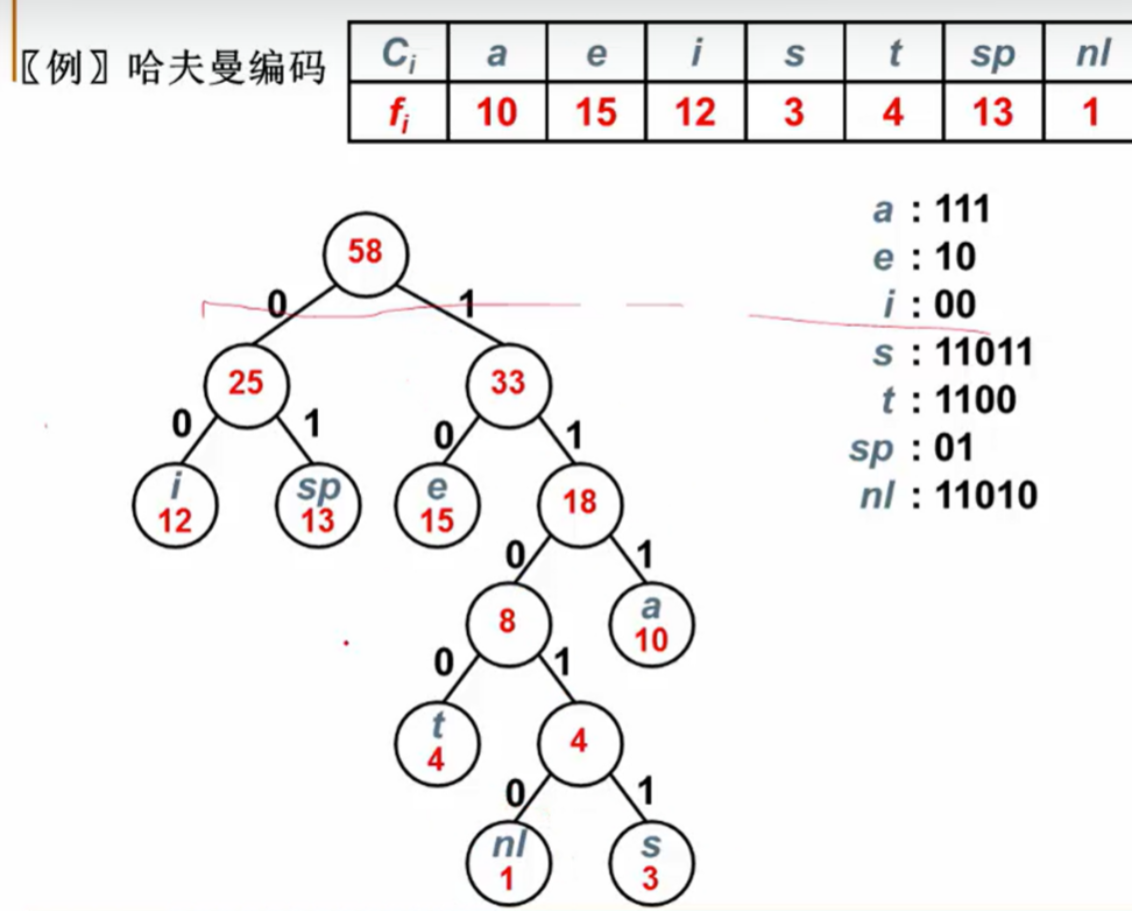
给定字符串 “AAABBCC”，用哈夫曼编码可以为频率高的字符 A 分配较短的编码（如 0），为频率低的字符 B 和 C 分配较长的编码。

分析：

  1. 用等长ASCII编码：58×8 = 464位

  2. 用等长3位编码：58×3 = 174位;

  3. 不等长编码：出现频率高的字符用的编码短些，出现频率低的字符则可以编码长些？

怎么进行不等长编码？

如何避免二义性(就是你这个编码不止一个意思)

  1. 前缀码prefix code：任何字符的编码都不是另一字符编码的前缀

    • 可以无二义地解码(你的这个编码不能是其他编码的前缀)

  2. 二叉树用于编码：

    • 左右分支：0、1

    • 字符只在叶结点上

    • 怎么构造一颗编码代价最小的二叉树？

3 集合及运算

3.1 集合的表示及查找

集合运算包括交集、并集、差集等操作。

并查集（Union-Find）：

并查集是一种用于处理动态连通性问题的树形结构。它支持两个主要操作：

  • 查找（Find）：查找某元素所属的集合。

    int Find(SetType S[],ElementType X)
{
    //在数组S中查找值为X的元素所属的集合
    //MaxSize是全局变量，为数组S的最大长度
    int i;
    for(i = 0;i < MaxSize && S[i].Data != X; i++);
    if(i >= MaxSize) return -1;//未找到X,返回-1
    for(;S[i].Parent >= 0; i = S[i].Parent);//Parent的值为-1的时候就是找到根结点。i = S[i].Parent：原本指向i的位置现在跳到了s[i].Parent
    return i;//找到X所属集合，返回树根结点在数组S中的下标
}

  • 合并（Union）：合并两个元素所属的集合。

集合的树结构表示：

每个元素是一个节点，每个集合是由这些元素组成的树。根节点表示集合的代表元素，父节点指向上级节点。

3.2 集合的并运算

并运算的实现通过找到两个元素的根节点，然后将其中一个根节点指向另一个根节点。

void Union(SetType S[ ],ElementType X1,ElementType X2 )
{
    int Root1,Root2;
    Root1 = Find(S,X1);//得到X1与X2对应的树根
    Root2 = Find(S,X2);
    if( Root1 != Root2 ) S[Root2].Parent = Root1;//判断如果不是本身就是同一个集合的，如果是同一个集合的话就不需要做这个并的操作。不同则合并
}
优化：

为了减少树的高度，提高查找效率，可以采用按秩合并或按大小合并的方法，将较小的树合并到较大的树上。

小测验：

已知 a 和 b 均为所在集合的根节点，分别位于数组分量3和2位置上，parent值分别为-3和-2。按集合大小合并后，a 和 b 的 parent 值分别是 -5 和 3。

集合的定义与并查

#define MAXN 1000                  /* 集合最大元素个数 */
typedef int ElementType;           /* 默认元素可以用非负整数表示 */
typedef int SetName;               /* 默认用根结点的下标作为集合名称 */
typedef ElementType SetType[MAXN]; /* 假设集合元素下标从0开始 */

void Union( SetType S, SetName Root1, SetName Root2 )
{ /* 这里默认Root1和Root2是不同集合的根结点 */
    /* 保证小集合并入大集合 */
    if ( S[Root2] < S[Root1] ) { /* 如果集合2比较大 */
        S[Root2] += S[Root1];     /* 集合1并入集合2  */
        S[Root1] = Root2;
    }
    else {                         /* 如果集合1比较大 */
        S[Root1] += S[Root2];     /* 集合2并入集合1  */
        S[Root2] = Root1;
    }
}

SetName Find( SetType S, ElementType X )
{ /* 默认集合元素全部初始化为-1 */
    if ( S[X] < 0 ) /* 找到集合的根 */
        return X;
    else
        return S[X] = Find( S, S[X] ); /* 路径压缩 */

4 小白专场：堆中的路径

题目描述：

给定5个数据构成一个最小堆，并进行3次查询。查询的目的是给定堆中的某个节点，求从根节点到该节点的路径。

解决思路：

将给定的数据插入堆中，维护堆的有序性。查询时，逐层向上追溯，从给定节点回到根节点，并记录路径。

堆的表示及其操作(堆是一种按一定顺序组织的完全二叉树)
#define MAXN 1001
#define MINH -10001

int H[MAXN],size;//由于堆在存储的时候是把根结点放在数组下标为1的地方，也就是说0是空缺的
//这样子按照一层层顺序逐个往数组后面存放，使得堆中的任何一个元素可以很容易的找到他的父节点在哪里，左右儿子在哪里
//整数size表示当前堆大小
void Create()//堆的初始化，就是建立一个空堆(size设置为0)
{
    size = 0;
    H[0] = MINH;//设置岗哨
}
//插入操作
void Insert(int X)
{
    //将X插入H。这里省略检查堆是否已满的代码
    int i;
    for(i = ++size;H[i/2]>X;i/=2)
        H[i] = H[i/2];//i挪到父节点(i/2)的位置
    H[i] = X;
}

主程序
    int main()
{
    1.读入n和m
    2.根据输入序列建堆
    3.对m个要求：打印到根的路径
        
        return 0;
}
//具体实现程序
int main()
{
    int n,m,x,i,j;
    
    scanf("%d%d",&n,&m);
    Create();//堆初始化
    for(i = 0;i < n; i++ ) {//以逐个插入方式建堆
        scanf("%d",&x);
        Insert(x);//利用Insert函数插到堆中
    }
    //m个查询
    for(i=0;i<m;i++){
        scanf("%d",&j);
        printf("d",H[j]);
        while(j < 1){//沿根方向输出各结点(也就是说把他的祖先全部打印出来了)当j>1是代表还没有到根的时候，根的位置是1，这时候j/2就代表了他父节点的位置
            j /= 2;
            printf("%d",H[j]);
        }
        printf("\n");
    }
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2148679.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

YOLOv9改进策略【注意力机制篇】| MCAttention 多尺度交叉轴注意力

YOLOv9改进策略【注意力机制篇】| MCAttention 多尺度交叉轴注意力

一、本文介绍 本文记录的是基于MCA注意力模块的YOLOv9目标检测改进方法研究。普通的轴向注意力难以实现长距离交互&#xff0c;不利于捕获分割任务中所需的空间结构或形状&#xff0c;而MCA注意力模块通过构建了两个并行轴向注意力之间的交互&#xff0c;更有效地利用多尺度特…
阅读更多...
2.4 卷积2

2.4 卷积2

2.4.2 复正弦波与整体方案 在2.3节中&#xff0c;我们提出了关于复正弦输入的频域输出及其意义的两个问题。为了研究这些问题&#xff0c;我们让一个具有真实脉冲响应 h [ n ] h[n] h[n]&#xff08;即 h Q [ n ] 0 h_Q[n] 0 hQ​[n]0&#xff09;的LTI系统通过输入复正弦…
阅读更多...
数据结构（Day16）

数据结构（Day16）

一、学习内容 1、有关顺序表的操作&#xff08;功能函数&#xff09; 1、创建顺序表 Plist create_list(){Plist L malloc(sizeof(list)); // 为顺序表分配内存空间if(NULL L){printf("申请空间失败\n");return NULL; // 如果内存分配失败&#xff0c;返回 NU…
阅读更多...
RTMP协议在无人机巡检中的应用场景

RTMP协议在无人机巡检中的应用场景

为什么要用无人机巡检 好多开发者对无人机巡检技术方案&#xff0c;相对陌生&#xff0c;实际上&#xff0c;无人机巡检就是利用无人机对特定区域或设施进行定期或不定期的检查。这种巡检方式相比传统的人工巡检具有显著的优势&#xff0c;包括速度快、覆盖广、风险低、准确性…
阅读更多...
Tornado 是一个 Python 异步网络库和 web 框架

Tornado 是一个 Python 异步网络库和 web 框架

Tornado 是一个 Python 异步网络库和 web 框架&#xff0c;它最初由 FriendFeed 开发&#xff0c;后来被 Facebook 收购并开源。Tornado 因其非阻塞的 I/O 操作和优秀的性能而广受欢迎&#xff0c;特别是在需要处理大量并发连接的应用中。Tornado 的底层实现主要依赖于 Python …
阅读更多...
神经网络通俗理解学习笔记(0) numpy、matplotlib

神经网络通俗理解学习笔记(0) numpy、matplotlib

Numpy numpynumpy 基本介绍Ndarray对象及其创建Numpy数组的基础索引numpy数组的合并与拆分&#xff08;重要&#xff09;numpy数组的矩阵运算Numpy数组的统计运算numpy中的arg运算numpy中的神奇索引和比较 Matplotlib numpy numpy 基本介绍 numpy 大多数机器学习库都用了这个…
阅读更多...
【Linux入门】基本指令（一）

【Linux入门】基本指令（一）

目录 一.使用环境 二.快捷键 三. 登录与用户管理 1.ssh root[ip地址] 2.whoami 3.ls /home 4.adduser [用户名] 5.passwd [用户名] 四.目录文件操作 1.ls 2.pwd 3.cd 4.touch 5.mkdir 6.rm 7.cp 五.命令手册 一.使用环境 云服务器&#xff1a;市面上有很多&am…
阅读更多...
Python 中的 typing 模块常见用法

Python 中的 typing 模块常见用法

typing 模块是 Python 提供的一个标准库&#xff0c;主要用于为函数、变量和类定义类型提示&#xff08;Type Hints&#xff09;&#xff0c;从而提高代码的可读性和类型安全性。虽然 Python 是动态类型语言&#xff0c;但通过 typing 模块&#xff0c;开发者可以明确指定变量和…
阅读更多...
TMStarget学习——Functional Connectivity

TMStarget学习——Functional Connectivity

今天基于结构像和功能像数据试验操作TMStarget 的第二个功能模块Functional Connectivity。参考季老师的文档PPT来学习的&#xff0c;整个处理过程蛮长的&#xff0c;可能配置原因一路上报错也比较多&#xff0c;下面还是逐步记录吧&#xff0c;后面采用连更的方式直到跑通后再…
阅读更多...
C++ 中的继承（详细讲解）

C++ 中的继承（详细讲解）

一、继承的概念以及定义 1、继承概念 继承(inheritance)机制是面向对象程序设计使代码可以复用的最重要的手段&#xff0c;它允许程序员在保 持原有类特性的基础上进行扩展&#xff0c;增加功能&#xff0c;这样产生新的类&#xff0c;称派生类。继承呈现了面向对象 程序设计的…
阅读更多...
微波无源器件 功分器 4 一种用于天线阵列的紧凑宽带四路双极化波导功分器

微波无源器件 功分器 4 一种用于天线阵列的紧凑宽带四路双极化波导功分器

摘要&#xff1a; 一种新型紧凑和高效率&#xff0c;在一个同相2x4方案(四路)显示双极化的功分器的设计和仿真被提出了&#xff0c;两个基本的正交模式TE10和TE01在四个方波导处同相输出通过使用四个3端口个四个E面和两个H面功分结构。此功分末端接了两个商用波导(WR75)端口&am…
阅读更多...
青柠视频云——如何开启HTTPS服务?

青柠视频云——如何开启HTTPS服务?

前言 由于青柠视频云的语音对讲会使用到HTTPS服务&#xff0c;这里我们说一下如何申请证书以及如何在实战中部署并且配置使用。 一、证书申请 1、进入控制台 我们拿阿里云的免费个人证书为例&#xff0c;首先登录阿里云&#xff0c;在控制台找到数字证书管理服务&#xff0c;进…
阅读更多...
膨胀罐选型计算和其他事项

膨胀罐选型计算和其他事项

膨胀罐&#xff0c;也称定压罐、气压罐&#xff0c;广泛应用于空调、太阳能、锅炉等暖通系统以及供水和消防设备&#xff0c;缓冲系统压力波动&#xff0c;消除水锤&#xff0c;起到稳压卸荷的作用。在空调、太阳能、锅炉、地暖等闭式循环系统中&#xff0c;膨胀罐的作用是在工…
阅读更多...
3.数据类型

3.数据类型

作业系统链接 Python 是一门面向对象友好的语言&#xff0c;支持多种内置数据类型&#xff0c;包括整数&#xff08;int&#xff09;、浮点数&#xff08;float&#xff09;、布尔值&#xff08;bool&#xff09;、字符串&#xff08;str&#xff09;、列表&#xff08;list&am…
阅读更多...
直流电表如何在新能源领域进行应用

直流电表如何在新能源领域进行应用

直流电表在新能源领域的应用广泛且深入&#xff0c;其高精度、实时监测和数据分析能力为新能源系统的运行、管理和优化提供了重要支持。 一、太阳能光伏发电系统 在太阳能光伏发电系统中&#xff0c;直流电表扮演着至关重要的角色。太阳能电池板将光能转化为直流电能&#xf…
阅读更多...
.NET 一直跻身 30 大Github最活跃开源项目之列。

.NET 一直跻身 30 大Github最活跃开源项目之列。

大家好&#xff0c;我是编程乐趣。 一直以来都在介绍.Net的热门开源项目&#xff0c;今天来说说.Net本身。 .Net在GitHub上也是一个开源项目&#xff0c;.NET 是一个由 Microsoft 和 .NET 社区共同维护的开源跨平台框架。 自 2017 年以来&#xff0c;.NET 一直是 GitHub 上最…
阅读更多...
新手教学系列——非正常关机导致MySQL权限表（db）损坏及修复详解

新手教学系列——非正常关机导致MySQL权限表（db）损坏及修复详解

在使用MySQL的过程中，我们常常会遇到一些问题，尤其是当服务器或主机非正常关机或重启时，MySQL的某些表，特别是权限表（如 mysql.db 表），可能会损坏，导致数据库无法启动或访问。这种情况对生产环境的数据库系统来说是相当严重的，因此掌握修复方法非常重要。 本篇文章将…
阅读更多...
分享两个ADG监控脚本

分享两个ADG监控脚本

分享两个监控脚本&#xff0c;用于监控Oracle ADG的状态&#xff0c;如果状态异常则发送邮件告警 脚本一&#xff1a; 利用语句查询日志的应用状态&#xff0c;如果长时间未应用则邮件告警&#xff0c;提醒DBA检查ADG的状态是否异常&#xff1b; 阈值条件&#xff1a;最近一…
阅读更多...
关于用matplotlib.pyplot加载图片颜色不对的解决方法

关于用matplotlib.pyplot加载图片颜色不对的解决方法

1.原理&#xff1a;用opencv加载的图片是BGR存储的。而用matplotlib.pyplot 需要RGB的格式,故在加载之前使用下面的语句改成RGB格式。 img2 cv2.cvtColor(img, cv2.COLOR_BGR2RGB) # 或使用 # img2 img[:, :, ::-1]#将图像img的颜色通道进行反转。 ::-1 表示在最后一个维度…
阅读更多...
财富通公司开发维修售后小程序，解决售后维修问题

财富通公司开发维修售后小程序，解决售后维修问题

财富通公司为广大用户开发的维修售后小程序&#xff0c;旨在便捷地解决售后维修问题&#xff0c;提升用户体验&#xff0c;增强客户粘性。以下是该小程序如何具体解决售后维修问题的几个关键点&#xff1a; 一. 一站式报修流程 1.简化操作&#xff1a;用户只需通过小程序几步…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023