目录
一、Floyd算法与A * 算法
1、Floyd算法
思想
伪代码
2、 A * 算法
思想
伪代码
二、经典题目
题目一:卡码网 97. 小明逛公园
题目链接
题解:Floyd 算法
题目二:卡码网 127. 骑士的攻击
题目链接
题解:A * 算法(A-Star)
三、小结
一、Floyd算法与A * 算法
1、Floyd算法
思想
Floyd算法的基本思想是逐步迭代地考虑图中的所有顶点,并更新任意两点之间的最短路径长度。在每一步迭代中,算法检查所有顶点对(i,j),并通过当前考虑的顶点k,看是否能够找到一条从i到j的更短路径。具有能够找到图中任意两点间的最短路径的优势,适合解决多源最短路,即求多个起点到多个终点的多条最短路径。
Floyd算法核心思想是动态规划。
伪代码
function floydWarshall(weights, V):
let dist be a V x V array
for i from 0 to V-1:
for j from 0 to V-1:
if i == j:
dist[i][j] = 0
else if there is an edge from i to j:
dist[i][j] = weight of the edge from i to j
else:
dist[i][j] = INFINITY
for k from 0 to V-1:
for i from 0 to V-1:
for j from 0 to V-1:
if dist[i][k] + dist[k][j] < dist[i][j]:
dist[i][j] = dist[i][k] + dist[k][j]
return dist
2、 A * 算法
入门建议观看视频:【A*寻路算法详解 #A星 #启发式搜索】
思想
A算法(A-Star算法)是一种在图形平面上,有多个节点的路径中,寻找一条从起点到终点的最短路径的算法。它的设计思想主要结合了实际代价和启发式估计,以高效地搜索图形中的最优路径。
核心思想是将启发式搜索和最佳优先搜索结合起来,以寻找从起始点到目标点的最短路径。
伪代码
function A*(start, goal)
open_list = priority_queue() // 优先队列,按f值排序
start.g = 0
start.h = heuristic(start, goal)
start.f = start.g + start.h
start.parent = null
open_list.add(start)
while not open_list.is_empty()
current = open_list.pop() // 取出f值最小的节点
if current == goal
return reconstruct_path(current)
closed_list.add(current) // 将当前节点加入封闭列表
for neighbor in neighbors(current)
if neighbor in closed_list
continue
tentative_g = current.g + distance(current, neighbor)
if neighbor not in open_list or tentative_g < neighbor.g
neighbor.parent = current
neighbor.g = tentative_g
neighbor.h = heuristic(neighbor, goal)
neighbor.f = neighbor.g + neighbor.h
if neighbor not in open_list
open_list.add(neighbor)
return null // 没有找到路径
function reconstruct_path(node)
path = []
while node is not null
path.prepend(node)
node = node.parent
return path.reverse() // 反转路径以从起点到终点
function heuristic(node, goal)
// 返回从node到goal的启发式估计值
end function
function neighbors(node)
// 返回node的邻居节点列表
end function
function distance(node1, node2)
// 返回从node1到node2的实际距离
end function
二、经典题目
题目一:卡码网 97. 小明逛公园
题目链接
97. 小明逛公园 (kamacoder.com)
题目描述
小明喜欢去公园散步,公园内布置了许多的景点,相互之间通过小路连接,小明希望在观看景点的同时,能够节省体力,走最短的路径。
给定一个公园景点图,图中有 N 个景点(编号为 1 到 N),以及 M 条双向道路连接着这些景点。每条道路上行走的距离都是已知的。
小明有 Q 个观景计划,每个计划都有一个起点 start 和一个终点 end,表示他想从景点 start 前往景点 end。由于小明希望节省体力,他想知道每个观景计划中从起点到终点的最短路径长度。 请你帮助小明计算出每个观景计划的最短路径长度。
输入描述
第一行包含两个整数 N, M, 分别表示景点的数量和道路的数量。
接下来的 M 行,每行包含三个整数 u, v, w,表示景点 u 和景点 v 之间有一条长度为 w 的双向道路。
接下里的一行包含一个整数 Q,表示观景计划的数量。
接下来的 Q 行,每行包含两个整数 start, end,表示一个观景计划的起点和终点。
输出描述
对于每个观景计划,输出一行表示从起点到终点的最短路径长度。如果两个景点之间不存在路径,则输出 -1。
输入示例
7 3 2 3 4 3 6 6 4 7 8 2 2 3 3 4输出示例
4 -1提示信息
从 2 到 3 的路径长度为 4,3 到 4 之间并没有道路。
1 <= N, M, Q <= 1000.
题解:Floyd 算法
关键在于Floyd算法的实现,即:
使用三重循环来实现Floyd算法:
外层循环变量 k 代表中间节点,内两层循环变量 i 和 j 分别代表起点和终点。
在每一轮循环中,检查通过中间节点 k 从 i 到 j 的路径是否比当前已知的路径更短,如果是,则更新 grid[i][j]。
代码实现:
for (int k = 1; k <= n; k++) // k代表中间节点
{
for (int i = 1; i <= n; i++) // i代表起点
{
for (int j = 1; j <= n; j++) // j代表终点
{
grid[i][j] = min(grid[i][j], grid[i][k] + grid[k][j]); // 更新i到j的最短路径,如果通过k的路径更短,则更新
}
}
}完整代码如下:
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n, m, p1, p2, val;
cin >> n >> m;
vector<vector<int>> grid(n + 1, vector<int>(n + 1, 10005)); // 创建一个二维向量grid来存储图的邻接矩阵,因为边的最大距离为10**4
// 读取m条边的信息,并更新邻接矩阵
for (int i = 0; i < m; i++)
{
cin >> p1 >> p2 >> val;
grid[p1][p2] = val;
grid[p2][p1] = val; // 注意这里是双向图:需要考虑两个方向
}
// 开始 floyd 算法
for (int k = 1; k <= n; k++) // k代表中间节点
{
for (int i = 1; i <= n; i++) // i代表起点
{
for (int j = 1; j <= n; j++) // j代表终点
{
grid[i][j] = min(grid[i][j], grid[i][k] + grid[k][j]); // 更新i到j的最短路径,如果通过k的路径更短,则更新
}
}
}
// 输出结果
int Q, start, end;
cin >> Q;
while (Q--)
{
cin >> start >> end;
if (grid[start][end] == 10005) // 如果最短路径长度仍然是初始值,表示没有路径
cout << -1 << endl;
else
cout << grid[start][end] << endl;
}
return 0;
}
题目二:卡码网 127. 骑士的攻击
题目链接
127. 骑士的攻击 (kamacoder.com)
题目描述
在象棋中,马和象的移动规则分别是“马走日”和“象走田”。现给定骑士的起始坐标和目标坐标,要求根据骑士的移动规则,计算从起点到达目标点所需的最短步数。
棋盘大小 1000 x 1000(棋盘的 x 和 y 坐标均在 [1, 1000] 区间内,包含边界)
输入描述
第一行包含一个整数 n,表示测试用例的数量,1 <= n <= 100。
接下来的 n 行,每行包含四个整数 a1, a2, b1, b2,分别表示骑士的起始位置 (a1, a2) 和目标位置 (b1, b2)。
输出描述
输出共 n 行,每行输出一个整数,表示骑士从起点到目标点的最短路径长度。
输入示例
6 5 2 5 4 1 1 2 2 1 1 8 8 1 1 8 7 2 1 3 3 4 6 4 6输出示例
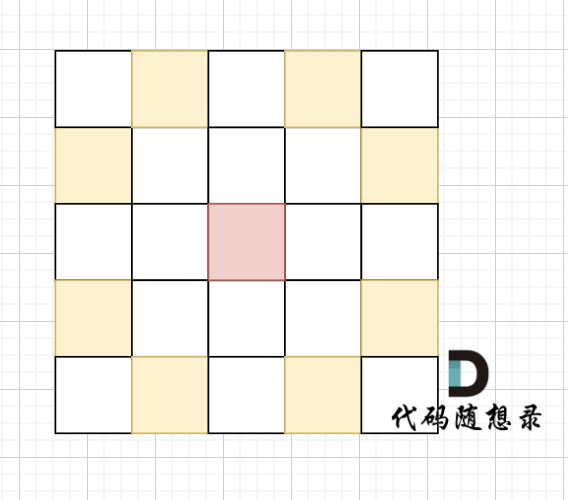
2 4 6 5 1 0提示信息
骑士移动规则如图,红色是起始位置,黄色是骑士可以走的地方。
题解:A * 算法(A-Star)
关键在于A*算法实现的部分:
在astar函数中,使用优先队列来存储当前的Knight对象;
循环直到优先队列为空,即所有可能的路径都被检查过;
在每次循环中,从优先队列中取出F值最小的Knight对象,并检查是否到达目标位置;
如果未到达目标位置,则遍历8个可能的方向,计算下一个位置的坐标,并检查是否越界或已经被访问过;
如果下一个位置合法且未被访问过,则更新路径消耗,计算F值,并将其加入优先队列;
当到达目标位置时,循环结束。
实现代码:
void astar(const Knight &k)
{
Knight cur, next;
que.push(k);
while (!que.empty())
{
cur = que.top();
que.pop();
if (cur.x == b1 && cur.y == b2)
break;
for (int i = 0; i < 8; i++) // 遍历骑士的8个可能移动方向
{
// 得到下一个位置的坐标
next.x = cur.x + dir[i][0];
next.y = cur.y + dir[i][1];
if (next.x < 1 || next.x > 1000 || next.y < 1 || next.y > 1000) // 如果下一个位置越界,则跳过
continue;
if (!moves[next.x][next.y]) // 如果下一个位置没有被访问过
{
moves[next.x][next.y] = moves[cur.x][cur.y] + 1; // 更新下一个位置的路径消耗
// 开始计算F
next.g = cur.g + 5; // 统一不开根号,这样可以提高精度,马走日,1 * 1 + 2 * 2 = 5
next.h = Heuristic(next); // 计算当前节点到终点的预估消耗
next.f = next.g + next.h; // 计算F值
que.push(next); // 将下一个位置的Knight对象加入优先队列
}
}
}
}完整代码实现:
#include <bits/stdc++.h>
using namespace std;
int moves[1001][1001]; // 定义一个二维数组moves,用于存储骑士从起点到当前位置的移动步数
int dir[8][2] = {-2, -1, -2, 1, -1, 2, 1, 2, 2, 1, 2, -1, 1, -2, -1, -2}; // 定义一个方向数组dir,用于存储骑士可能的移动方向
int b1, b2;
struct Knight // 定义一个结构体Knight,用于存储骑士的当前位置和路径消耗等信息
{
int x, y;
int g, h, f;
bool operator<(const Knight &k) const // 重载运算符,用于优先队列的排序
{
return k.f < f; // 从小到大排序
}
};
priority_queue<Knight> que; // 定义一个优先队列que,用于存储Knight对象,并按照f值排序
int Heuristic(const Knight &k) // 欧拉距离
{
return (k.x - b1) * (k.x - b1) + (k.y - b2) * (k.y - b2); // 统一不开根号,这样可以提高精度
}
// 执行A*算法:参数k是当前的Knight对象
void astar(const Knight &k)
{
Knight cur, next;
que.push(k);
while (!que.empty())
{
cur = que.top();
que.pop();
if (cur.x == b1 && cur.y == b2)
break;
for (int i = 0; i < 8; i++) // 遍历骑士的8个可能移动方向
{
// 得到下一个位置的坐标
next.x = cur.x + dir[i][0];
next.y = cur.y + dir[i][1];
if (next.x < 1 || next.x > 1000 || next.y < 1 || next.y > 1000) // 如果下一个位置越界,则跳过
continue;
if (!moves[next.x][next.y]) // 如果下一个位置没有被访问过
{
moves[next.x][next.y] = moves[cur.x][cur.y] + 1; // 更新下一个位置的路径消耗
// 开始计算F
next.g = cur.g + 5; // 统一不开根号,这样可以提高精度,马走日,1 * 1 + 2 * 2 = 5
next.h = Heuristic(next); // 计算当前节点到终点的预估消耗
next.f = next.g + next.h; // 计算F值
que.push(next); // 将下一个位置的Knight对象加入优先队列
}
}
}
}
int main()
{
int n, a1, a2;
cin >> n;
while (n--)
{
cin >> a1 >> a2 >> b1 >> b2;
memset(moves, 0, sizeof(moves)); // 每次循环都初始化moves数组为0,确保每个骑士问题都有独立的路径记录
// 定义起点Knight对象start
// F = G + H
// G = 从起点到该节点路径消耗
// H = 该节点到终点的预估消耗
Knight start;
start.x = a1;
start.y = a2;
start.g = 0;
start.h = Heuristic(start);
start.f = start.g + start.h;
// 执行A*算法,以起点Knight对象start为起点
astar(start);
// 执行A*算法后,清空优先队列que,以便下一次循环使用
while (!que.empty())
que.pop();
cout << moves[b1][b2] << endl; // 输出本次从起点到目标点的路径消耗,即moves[b1][b2]
}
return 0;
}
三、小结
这算是图论最后的内容了,难度很大,个人感觉只是理解了大概意思,却难以代码实现,后边二刷的时候会强化理解,继续加油!