第2章 数据结构中栈与队列的概念

news2025/1/11 7:44:12

文章目录

    • 文档配套视频讲解链接地址
    • 第02 章 栈与队列
      • 2.1 栈与队列的框图
      • 2.2 栈
        • 1. 栈的概念
        • 2. 顺序栈
        • 3. 实例11 顺序栈
        • 4. 实例12 链式栈
      • 2.3 队列
        • 1. 队列的概念
        • 2. 顺序队列
        • 3. 实例13 顺序队列
        • 4. 链式队列
        • 5. 实例14 链式队列
      • 2.4 实例15 球钟问题
      • 2.5 队列与栈的转换
        • 1. 实例16 顺序的双栈实现一个队列
        • 2. 实例17 链式的双栈实现一个队列
        • 3. 实例18 顺序的双队列实现一个栈
        • 4. 实例19 链式的双队列实现一个栈

文档配套视频讲解链接地址

  1. 腾讯课堂视频链接地址 : 14_栈与队列_顺序栈
  2. 腾讯课堂视频链接地址 : 15_栈与队列_链式栈
  3. 腾讯课堂视频链接地址 : 16_栈与队列_循环队列
  4. 腾讯课堂视频链接地址 : 17_栈与队列_链式队列
  5. 腾讯课堂视频链接地址 : 18_栈与队列_顺序双栈一队列
  6. 腾讯课堂视频链接地址 : 19_栈与队列_顺序双队列一栈
  7. 腾讯课堂视频链接地址 : 20_栈与队列_链式双栈一队列
  8. 腾讯课堂视频链接地址 : 21_栈与队列_链式双栈一队列

第02 章 栈与队列

2.1 栈与队列的框图

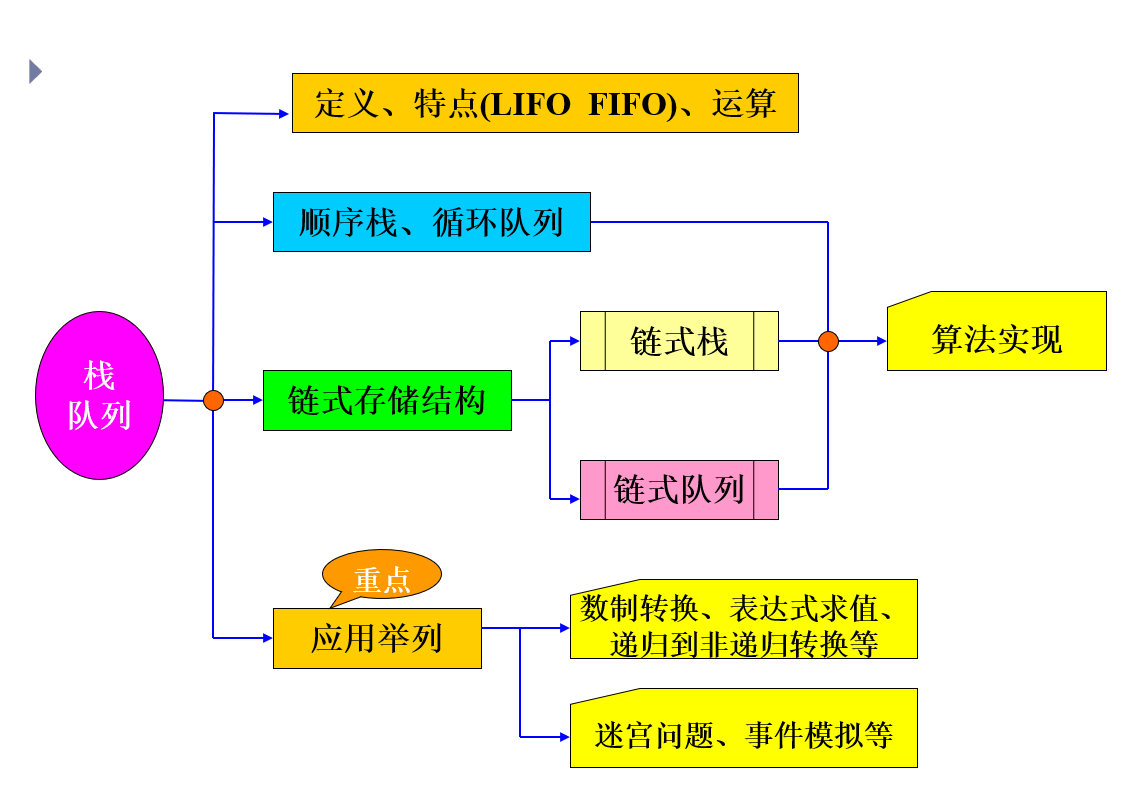
image-20220930091112124

2.2 栈

1. 栈的概念

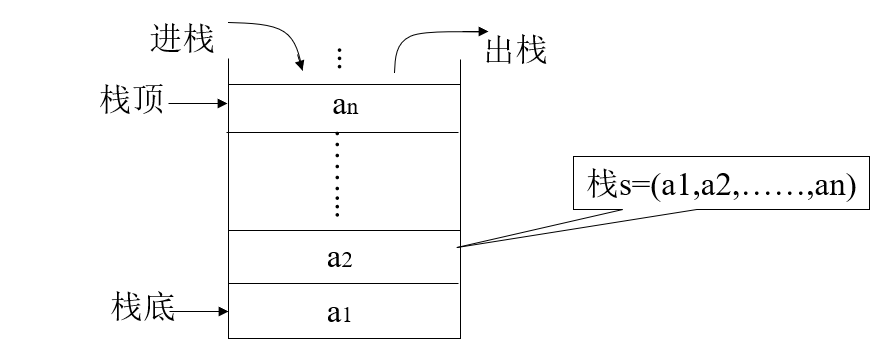
栈是限制在一端进行插入操作和删除操作的线性表（俗称堆栈），允许进行操作的一端称为“栈顶”，另一固定端称为“栈底”，当栈中没有元素时称为“空栈”。

  • 特点 ：后进先出（LIFO）Last In First Out
  • 类比事物 , 弹夹

image-20220930091504817

2. 顺序栈

  • 它是顺序表的一种，具有顺序表同样的存储结构，由数组定义，配合用数组下标表示的栈顶指针top（相对指针）完成各种操作。

3. 实例11 顺序栈

  • 源文件
04-ds/11-seqstack.c
  • 源代码
#include <stdio.h> 
#include <stdlib.h>
#include <string.h>
#include <error.h>

// sequeue stack 

#define  N   32 
typedef struct 
{
    int data[N]; // 数组的空间
    int index ; // 是数组下标的索引 

}seqstack_t; 

seqstack_t * create_empty_seqstack()
{
    seqstack_t * s = (seqstack_t *)malloc(sizeof(seqstack_t));
    memset(s->data,0,sizeof(s->data)) ; // 把数组中的内容清为0 
    s->index = -1 ; // 表示栈为空 
    return s ; 
}

int seqstack_is_empty(seqstack_t * s)
{
    return (s->index == -1 ); 
}

int seqstack_is_full(seqstack_t *s)
{
    return (s->index == N-1) ; 
}

// 入栈 , 压栈 
int seqstack_push(seqstack_t *s, int value)
{
    if(seqstack_is_full(s))
    {
        printf("栈已满"); 
        return -1 ;
    }
    s->index ++  ; 
    s->data[s->index] = value ; 
    return  0 ; 
}
int seqstack_pop(seqstack_t * s, int *pvalue)
{
    if(seqstack_is_empty(s))
    {
        printf("栈已空"); 
        return -1 ; 
    }
    *pvalue = s->data[s->index] ; 
    s->index -- ; 
    return 0 ; 
}

int main(int argc, char const *argv[])
{
    seqstack_t * S = create_empty_seqstack(); 
    printf("入栈顺序:");
    for(int i=0;i<33;i++)
    {
        printf("%d ",i+1); 
        seqstack_push(S,i+1); 
    }
    printf("\n"); 

    printf("出栈顺序:");
    for(int i=0,value;i<33;i++)
    {
        seqstack_pop(S,&value); 
        printf("%d ",value); 
    }
    printf("\n"); 

    
    
    return 0;
}
  • 运行结果
入栈顺序:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 栈已满
出栈顺序:32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 栈已空1

4. 实例12 链式栈

  • 源文件
04-ds/12-linkstack.c
  • 源代码
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <error.h>

// link stack

typedef struct node
{
    int data;
    struct node *next;
} linklist_t;

linklist_t *create_empty_linkstack()
{
    linklist_t *s = (linklist_t *)malloc(sizeof(linklist_t));
    s->data = 0;
    s->next = NULL;
    return s;
}

// 链表没有满  , 有空的概念
int linkstack_is_empty(linklist_t *s)
{
    return (s->next == NULL);
}

// 头部插入法
int linkstack_push(linklist_t *s, int value)
{
    linklist_t *p = (linklist_t *)malloc(sizeof(linklist_t));
    p->data = value;
    p->next = s->next;
    s->next = p;
    return 0;
}

// 头部删除法
int linkstack_pop(linklist_t *s, int *pvalue)
{
    linklist_t *p = s->next; // p 指向s的下一个节点
    if(linkstack_is_empty(s))
    {
        printf("栈已空"); 
        return -1 ; 
    }
    // s->next 不为空 
    s->next = p->next; // 接链表 
    *pvalue = p->data ; // 读取数据
    free(p); 
    return 0;
}

int main(int argc, char const *argv[])
{
    linklist_t *S = create_empty_linkstack();
    printf("入栈顺序:");
    for(int i=0;i<33;i++)
    {
        if( linkstack_push(S,i+1) ==  0 )  // 表示成功
        {
            printf("%d ",i+1);
        }
    }
    printf("\n");

    printf("出栈顺序:");
    for(int i=0,value;i<34;i++)
    {
        if(linkstack_pop(S,&value) == 0 )
        {
            printf("%d ",value);
        }

    }
    printf("\n");

    return 0;
}
  • 运行结果
入栈顺序:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 
出栈顺序:33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 栈已空

2.3 队列

1. 队列的概念

  • 队列是限制在两端进行插入操作和删除操作的线性表，允许进行存入操作的一端称为“队尾”，允许进行删除操作的一端称为“队头”。当线性表中没有元素时，称为“空队”。
  • 特点 ：先进先出（FIFO） First In First Out 。

2. 顺序队列

  • 它是顺序表的一种，具有顺序表同样的储存结构，由数组定义，配合用数组下标表示的队头指针和队尾指针完成各种操作。

3. 实例13 顺序队列

  • 源文件
04-ds/13-sequeue.c
  • 源代码
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// sequence queue

#define N 32
typedef struct
{
    int data[N];
    int front; // 队列的头  , 数组的下标
    int rear;  // 队列的尾  , 数组的下标
} sequeue_t;

// 空队列的概念是 : 队头等于队尾
// 为了区分空队 和满队 , 队列元素个数要比数组元素少一个
// 满队+1 等于空队
// 1 2 3 4 5
// f       f
// r

sequeue_t *create_empty_sequeue()
{
    sequeue_t *q = (sequeue_t *)malloc(sizeof(sequeue_t));
    memset(q->data, 0, sizeof(q->data));
    q->front = q->rear = N - 1; //指向数组最后一个元素
    return q;
}

int sequeue_is_empty(sequeue_t *q)
{
    return (q->front == q->rear);
}

int sequeue_is_full(sequeue_t *q)
{
    // 队尾 +1 == 队头 , 就是满队
    // 任何一个一个数对N求余 , 这个数的范围是  0 - N-1
    return ((q->rear + 1) % N == q->front);
}

int sequeue_enqueue(sequeue_t *q, int value)
{
    if (sequeue_is_full(q))
    {
        printf("队列已满");
        return -1;
    }
    q->rear = (q->rear + 1) % N; // 防止数组越界
    q->data[q->rear] = value;
    return 0;
}
int sequeue_dequeue(sequeue_t *q, int *pvalue)
{
    if (sequeue_is_empty(q))
    {
        printf("队列已空");
        return -1;
    }
    q->front = (q->front + 1) % N; // 防止数组越界
    *pvalue = q->data[q->front];
    return 0;
}

int main(int argc, char const *argv[])
{
    sequeue_t *Q = create_empty_sequeue();
    //  这个队列, 最多可以存放 31 个元素
    printf("入队顺序为:");
    for (int i = 0; i < 32; i++)
    {
        if (sequeue_enqueue(Q, i + 1) == 0)
        {
            printf("%d ", i + 1);
        }
    }
    printf("\n");

    printf("出队顺序为:");
    for (int i = 0,value; i < 32; i++)
    {
        if (sequeue_dequeue(Q, &value) == 0)
        {
            printf("%d ", value);
        }
    }
    printf("\n");
    return 0;
}
  • 运行结果
入队顺序为:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 队列已满
出队顺序为:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 队列已空

4. 链式队列

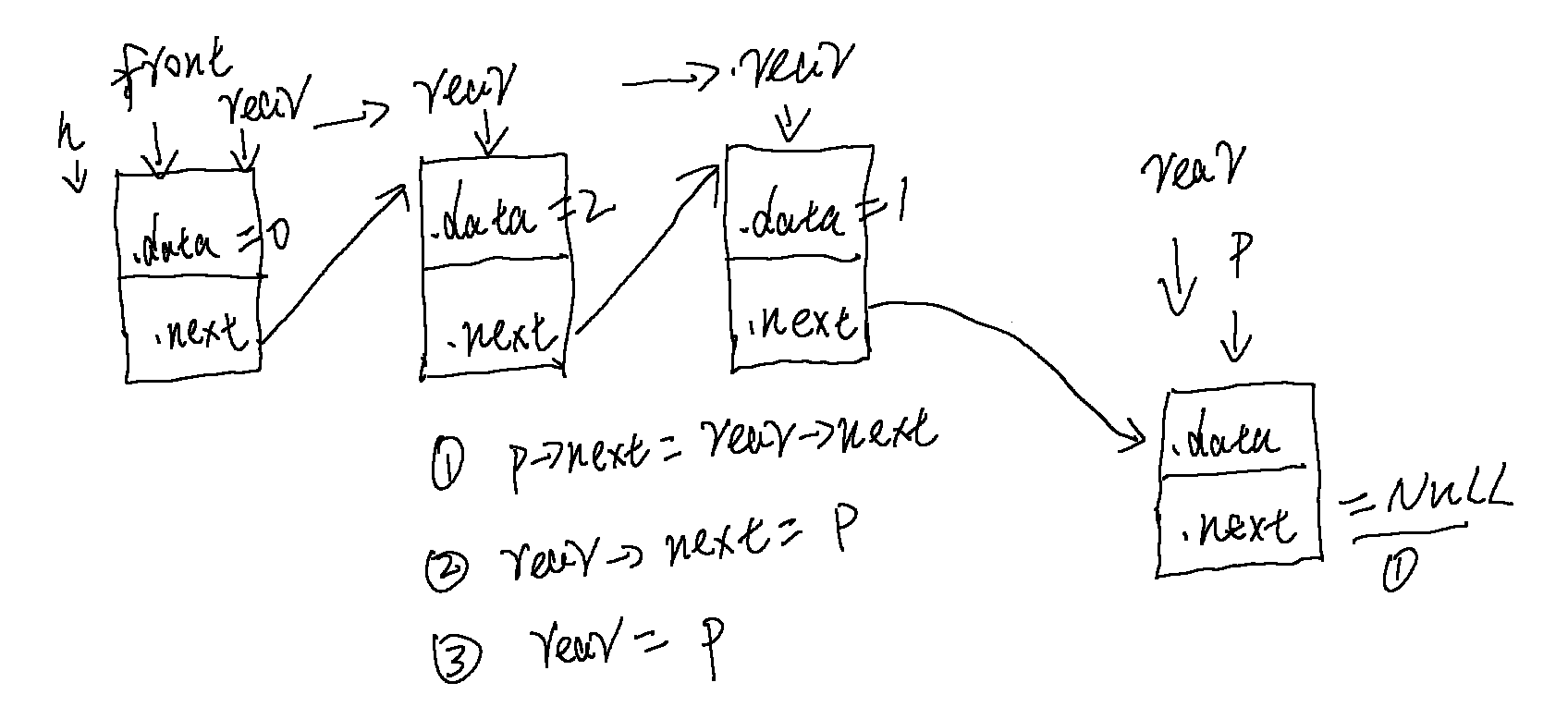
链式队列的尾部插入

image-20220930161025705

5. 实例14 链式队列

  • 源文件
04-ds/14-linkqueue.c
  • 源代码
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// sequence queue

typedef struct node
{
    int data;
    struct node *next;
} linklist_t;

typedef struct
{
    linklist_t *front; // 队头
    linklist_t *rear;  // 队尾
} linkqueue_t;

// 空队列的概念是 : 队头等于队尾
// 为了区分空队 和满队 , 队列元素个数要比数组元素少一个
// 满队+1 等于空队
// 1 2 3 4 5
// f       f
// r

linkqueue_t *create_empty_linkqueue()
{
    linklist_t *h = (linklist_t *)malloc(sizeof(linklist_t));
    linkqueue_t *q = (linkqueue_t *)malloc(sizeof(linkqueue_t));
    q->front = q->rear = h;
    q->front->data = 0;
    return q;
}

int linkqueue_is_empty(linkqueue_t *q)
{
    return (q->front == q->rear);
}

// 链式队列没有满的概念
// int linkqueue_is_full(linkqueue_t *q)
// {

// }

// 入队 队尾加
int linkqueue_enqueue(linkqueue_t *q, int value)
{
    linklist_t *p = (linklist_t *)malloc(sizeof(linklist_t));
    p->data = value;
    p->next = q->rear->next; // 尾部插入第1步
    q->rear->next = p;       // 尾部插入第2步
    q->rear = p;             // 尾部插入第3步
    return 0;
}

// 头部出队列 , 头部删除法
int linkqueue_dequeue(linkqueue_t *q, int *pvalue)
{
    linklist_t *p;
    if (linkqueue_is_empty(q))
    {
        printf("队列为空");
        return -1;
    }
    p = q->front->next;           // 头节点的下一个节点  , p是要删除的节点
    q->front->next = p->next;     // 接上链表
    if (q->front->next == NULL) // 此时队列为空
        q->rear = q->front; // 
    
    *pvalue = p->data;
    free(p);
    return 0;
}

int main(int argc, char const *argv[])
{
    linkqueue_t *Q = create_empty_linkqueue();
    //  这个队列, 最多可以存放 31 个元素
    printf("入队顺序为:");
    for (int i = 0; i < 32; i++)
    {
        if (linkqueue_enqueue(Q, i + 1) == 0)
        {
            printf("%d ", i + 1);
        }
    }
    printf("\n");

    printf("出队顺序为:");
    for (int i = 0, value; i < 33; i++)
    {
        if (linkqueue_dequeue(Q, &value) == 0)
        {
            printf("%d ", value);
        }
    }
    printf("\n");
    return 0;
}
  • 运行结果
入队顺序为:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 
出队顺序为:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 队列为空

2.4 实例15 球钟问题

  • 队列与栈应用

  • 问题描述：球钟是一个利用球的移动来记录时间的简单装置。它有三个可以容纳若干个球的指示器：分钟指示器，五分钟指示器，小时指示器。若分钟指示器中有2个球，五分钟指示器中有6个球，小时指示器中有5个球，则时间为5:32

  • 工作原理：每过一分钟，球钟就会从球队列的队首取出一个球放入分钟指示器，分钟指示器最多可容纳4个球。当放入第五个球时，在分钟指示器的4个球就会按照他们被放入时的相反顺序加入球队列的队尾。而第五个球就会进入五分钟指示器。按此类推，五分钟指示器最多可放11个球，小时指示器最多可放11个球。

  • 当小时指示器放入第12个球时，原来的11个球按照他们被放入时的相反顺序加入球队列的队尾，然后第12个球也回到队尾。这时，三个指示器均为空，回到初始状态，从而形成一个循环。因此，该球钟表示时间的范围是从0：00到11：59。

    现设初始时球队列的球数为27，球钟的三个指示器初态均为空。问，要经过多久，球队列才能回复到原来的顺序?

    Q : 是队列, 队列可以存放27个球

    S1: 是栈, 1分钟指示器, 里面可以存放5个球

    S5 : 是栈, 表示的5分钟的指示器, 里面可以存放12个球

    S60: 是栈, 表示小时指示器, 里面可以存放12个球

  • 源文件

04-ds/15-ballclock.c
  • 源代码
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// sequence queue

#define N 128
typedef struct
{
    int data[N];
    int front; // 队列的头  , 数组的下标
    int rear;  // 队列的尾  , 数组的下标
} sequeue_t;

// 空队列的概念是 : 队头等于队尾
// 为了区分空队 和满队 , 队列元素个数要比数组元素少一个
// 满队+1 等于空队
// 1 2 3 4 5
// f       f
// r

sequeue_t *create_empty_sequeue()
{
    sequeue_t *q = (sequeue_t *)malloc(sizeof(sequeue_t));
    memset(q->data, 0, sizeof(q->data));
    q->front = q->rear = N - 1; //指向数组最后一个元素
    return q;
}

int sequeue_is_empty(sequeue_t *q)
{
    return (q->front == q->rear);
}

int sequeue_is_full(sequeue_t *q)
{
    // 队尾 +1 == 队头 , 就是满队
    // 任何一个一个数对N求余 , 这个数的范围是  0 - N-1
    return ((q->rear + 1) % N == q->front);
}

int sequeue_is_size(sequeue_t *q)
{
    // 队尾减去队头就是元素的个数
    if (q->rear >= q->front) //
        return (q->rear - q->front);
    else
        return (N - q->front + q->rear);
}

int sequeue_enqueue(sequeue_t *q, int value)
{
    if (sequeue_is_full(q))
    {
        printf("队列已满");
        return -1;
    }
    q->rear = (q->rear + 1) % N; // 防止数组越界
    q->data[q->rear] = value;
    return 0;
}
int sequeue_dequeue(sequeue_t *q, int *pvalue)
{
    if (sequeue_is_empty(q))
    {
        printf("队列已空");
        return -1;
    }
    q->front = (q->front + 1) % N; // 防止数组越界
    *pvalue = q->data[q->front];
    return 0;
}

// sequeue stack
typedef struct
{
    int data[N]; // 数组的空间
    int index;   // 是数组下标的索引

} seqstack_t;

seqstack_t *create_empty_seqstack()
{
    seqstack_t *s = (seqstack_t *)malloc(sizeof(seqstack_t));
    memset(s->data, 0, sizeof(s->data)); // 把数组中的内容清为0
    s->index = -1;                       // 表示栈为空
    return s;
}

int seqstack_is_empty(seqstack_t *s)
{
    return (s->index == -1);
}

int seqstack_is_full(seqstack_t *s)
{
    return (s->index == N - 1);
}

int seqstack_is_size(seqstack_t *s)
{
    return (s->index+1);
}

// 入栈 , 压栈
int seqstack_push(seqstack_t *s, int value)
{
    if (seqstack_is_full(s))
    {
        printf("栈已满");
        return -1;
    }
    s->index++;
    s->data[s->index] = value;
    return 0;
}
int seqstack_pop(seqstack_t *s, int *pvalue)
{
    if (seqstack_is_empty(s))
    {
        printf("栈已空");
        return -1;
    }
    *pvalue = s->data[s->index];
    s->index--;
    return 0;
}

// 检查队列是否是 是否是1,2,3...27 这个顺序
// 是这个顺序 返回真 
// 不是这个顺序 返回假
int check_sequeue(sequeue_t * q)
{
    for(int i=1;i<27;i++)
    {
        // 正常顺序 1,2,3,4,...27 
        if(q->data[(q->front+i)%N] > q->data[(q->front+i+1)%N] )
        {
            return 0; // 这个顺序不对 
        }
    }
    return 1; // 所有顺序都对 , 返回真 

}

int main(int argc, char const *argv[])
{
    sequeue_t *Q = create_empty_sequeue(); // 创建一个空队列
    // 往队列中装入27个元素
    for (int i = 0; i < 27; i++)
    {
        sequeue_enqueue(Q, i + 1);
    }

    seqstack_t *S1 = create_empty_seqstack();  // S1 分钟指示器 
    seqstack_t *S5 = create_empty_seqstack();  // S5 5分钟指示器 
    seqstack_t *S60 = create_empty_seqstack(); // S60 5小时指示器 

    int count =0 ; //  用来记录工作的分钟数 
    int value = 0 ,t12;
    while(1)
    {
        count ++ ; // 计算累计时间的 
        sequeue_dequeue(Q,&value) ; // 从球队列中取出一个球
        seqstack_push(S1,value);    // 放入分钟指示器中

        /*************************************************************/
        // 分钟指示器的工作原理 

        if(seqstack_is_size(S1) < 5)  continue;

        seqstack_pop(S1,&value);  // 第五个球就会进入五分钟指示器
        seqstack_push(S5,value);  

        //在分钟指示器的4个球就会按照他们被放入时的相反顺序加入球队列的队尾
        for(int i=0;i<4;i++) 
        {
            seqstack_pop(S1,&value);  
            sequeue_enqueue(Q,value); 
        }
        /*************************************************************/
        // 5分钟指示器的工作原理 
        if(seqstack_is_size(S5) < 12)  continue;
        
        seqstack_pop(S5,&value);  // 第12个球就会进入小时指示器
        seqstack_push(S60,value);  

        //在5分钟指示器的11个球就会按照他们被放入时的相反顺序加入球队列的队尾
        for(int i=0;i<11;i++) 
        {
            seqstack_pop(S5,&value);  
            sequeue_enqueue(Q,value); 
        }

        /*************************************************************/
        // 小时指示器的工作原理 
        if(seqstack_is_size(S60) < 12)  continue;
        
        seqstack_pop(S60,&t12);  // 第12个球拿出来 

        //小时指示器的11个球就会按照他们被放入时的相反顺序加入球队列的队尾
        for(int i=0;i<11;i++) 
        {
            seqstack_pop(S60,&value);  
            sequeue_enqueue(Q,value); 
        }
        sequeue_enqueue(Q,t12);  // 然后第12个球也回到队尾

        /*************************************************************/
        // 结束条件 
        if(check_sequeue(Q)) // 为真, 返回 , 为假继续循环
        {
            break; 
        }
        else
        {
            continue;
        }
    }
    // 33120 是标准答案 
    printf("count = %d\n",count); 

    return 0;
}
  • 运行结果
count = 33120

2.5 队列与栈的转换

1. 实例16 顺序的双栈实现一个队列

  • 使用双栈实现一个队列

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QpQ8IKRT-1668935067808)(https://gitee.com/embmaker/cloudimage/raw/master/img/%E5%8F%8C%E6%A0%88%E5%AE%9E%E7%8E%B0%E4%B8%80%E9%98%9F%E5%88%97.jpg)]

  • 使用顺序的栈实现一个顺序的队列

    • 第1步:入栈s1中, 入栈1,2,3,4
    • 第2步:把s1中的元素全部出栈到s2中 ,s2中的值:4,3,2,1
    • 第3步:从s2中出栈一个元素,这个元素就是1 , 把1出栈
    • 第4步:把s2所有的元素再次出栈到s1当中
    • 最终s1 内为: 2,3,4

  • 源文件

04-ds/16-double_seqstack_one_sequeue.c
  • 源代码
#include <stdio.h> 
#include <stdlib.h>
#include <string.h>
#include <error.h>

// sequeue stack 

#define  N   32 
typedef struct 
{
    int data[N]; // 数组的空间
    int index ; // 是数组下标的索引 

}seqstack_t; 

seqstack_t * create_empty_seqstack()
{
    seqstack_t * s = (seqstack_t *)malloc(sizeof(seqstack_t));
    memset(s->data,0,sizeof(s->data)) ; // 把数组中的内容清为0 
    s->index = -1 ; // 表示栈为空 
    return s ; 
}

int seqstack_is_empty(seqstack_t * s)
{
    return (s->index == -1 ); 
}

int seqstack_is_full(seqstack_t *s)
{
    return (s->index == N-1) ; 
}

// 入栈 , 压栈 
int seqstack_push(seqstack_t *s, int value)
{
    if(seqstack_is_full(s))
    {
        printf("栈已满"); 
        return -1 ;
    }
    s->index ++  ; 
    s->data[s->index] = value ; 
    return  0 ; 
}
int seqstack_pop(seqstack_t * s, int *pvalue)
{
    if(seqstack_is_empty(s))
    {
        printf("栈已空"); 
        return -1 ; 
    }
    *pvalue = s->data[s->index] ; 
    s->index -- ; 
    return 0 ; 
}

int sequeue_enqueue(seqstack_t *s1,seqstack_t *s2,int value)
{
    seqstack_push(s1,value); 
    return 0; 
}
int sequeue_dequeue(seqstack_t *s1,seqstack_t *s2,int *pvalue)
{
    int value ; 
    // 1. 把s1中的所有元素倒入到s2中
    while(!seqstack_is_empty(s1))
    {
        seqstack_pop(s1,&value); 
        seqstack_push(s2,value); 
    }

    // 2. 出一个元素  
    seqstack_pop(s2,pvalue);

    // 3. 把s2中的所有元素倒入到s1中
    while(!seqstack_is_empty(s2))
    {
        seqstack_pop(s2,&value); 
        seqstack_push(s1,value); 
    }
    return 0 ; 
}


int main(int argc, char const *argv[])
{
    seqstack_t *S1 = create_empty_seqstack();
    seqstack_t *S2 = create_empty_seqstack();
    //  这个队列, 最多可以存放 31 个元素
    printf("入队顺序为:");
    for (int i = 0; i < 32; i++)
    {
        if (sequeue_enqueue(S1,S2, i + 1) == 0)
        {
            printf("%d ", i + 1);
        }
    }
    printf("\n");

    printf("出队顺序为:");
    for (int i = 0,value; i < 32; i++)
    {
        if (sequeue_dequeue(S1,S2, &value) == 0)
        {
            printf("%d ", value);
        }
    }
    printf("\n");
    
    
    return 0;
}
  • 运行结果
入队顺序为:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 
出队顺序为:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

2. 实例17 链式的双栈实现一个队列

  • 流程如实例16
  • 源文件
04-ds/17-double_linkstack_one_linkqueue.c
  • 源代码
#include <stdio.h> 
#include <stdlib.h>
#include <string.h>
#include <error.h>

// link stack

typedef struct node
{
    int data;
    struct node *next;
} linklist_t;

linklist_t *create_empty_linkstack()
{
    linklist_t *s = (linklist_t *)malloc(sizeof(linklist_t));
    s->data = 0;
    s->next = NULL;
    return s;
}

// 链表没有满  , 有空的概念
int linkstack_is_empty(linklist_t *s)
{
    return (s->next == NULL);
}

// 头部插入法
int linkstack_push(linklist_t *s, int value)
{
    linklist_t *p = (linklist_t *)malloc(sizeof(linklist_t));
    p->data = value;
    p->next = s->next;
    s->next = p;
    return 0;
}

// 头部删除法
int linkstack_pop(linklist_t *s, int *pvalue)
{
    linklist_t *p = s->next; // p 指向s的下一个节点
    if(linkstack_is_empty(s))
    {
        printf("栈已空"); 
        return -1 ; 
    }
    // s->next 不为空 
    s->next = p->next; // 接链表 
    *pvalue = p->data ; // 读取数据
    free(p); 
    return 0;
}

int linkqueue_enqueue(linklist_t *s1,linklist_t *s2,int value)
{
    linkstack_push(s1,value); 
    return 0; 
}
int linkqueue_dequeue(linklist_t *s1,linklist_t *s2,int *pvalue)
{
    int value ; 
    // 1. 把s1中的所有元素倒入到s2中
    while(!linkstack_is_empty(s1))
    {
        linkstack_pop(s1,&value); 
        linkstack_push(s2,value); 
    }

    // 2. 出一个元素  
    linkstack_pop(s2,pvalue);

    // 3. 把s2中的所有元素倒入到s1中
    while(!linkstack_is_empty(s2))
    {
        linkstack_pop(s2,&value); 
        linkstack_push(s1,value); 
    }
    return 0 ; 
}


int main(int argc, char const *argv[])
{
    linklist_t *S1 = create_empty_linkstack();
    linklist_t *S2 = create_empty_linkstack();
    //  这个队列, 最多可以存放 31 个元素
    printf("入队顺序为:");
    for (int i = 0; i < 32; i++)
    {
        if (linkqueue_enqueue(S1,S2, i + 1) == 0)
        {
            printf("%d ", i + 1);
        }
    }
    printf("\n");

    printf("出队顺序为:");
    for (int i = 0,value; i < 32; i++)
    {
        if (linkqueue_dequeue(S1,S2, &value) == 0)
        {
            printf("%d ", value);
        }
    }
    printf("\n");
    
    
    return 0;
}
  • 运行结果
入队顺序为:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 
出队顺序为:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

3. 实例18 顺序的双队列实现一个栈

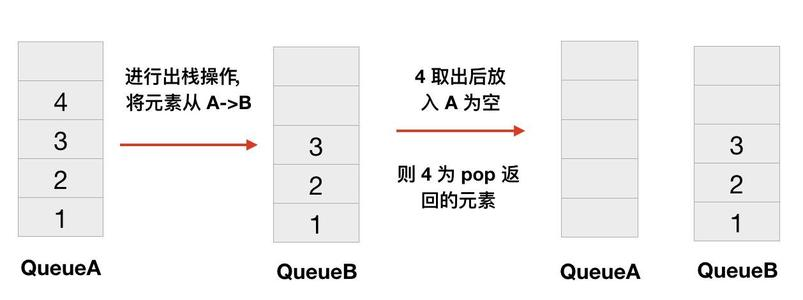
image-20221004145246840

  • 初始状态 QueueA 和QueueB都为空

  • 第1步: 把QueueA 入队1,2,3,4

  • 第2补: 把QueueA 出队1,2,3 到QueueB, 此时QueueA中还剩下一个4

  • 第3步: 从QueueA中出队最后一个元素4 , 4就是出栈的元素

  • 第4步: 把QueueB中的所有元素再入队到QueueA中, 此时一次出栈完成

  • 最后的效果是: QueueA中是 1,2,3 QueueB中空

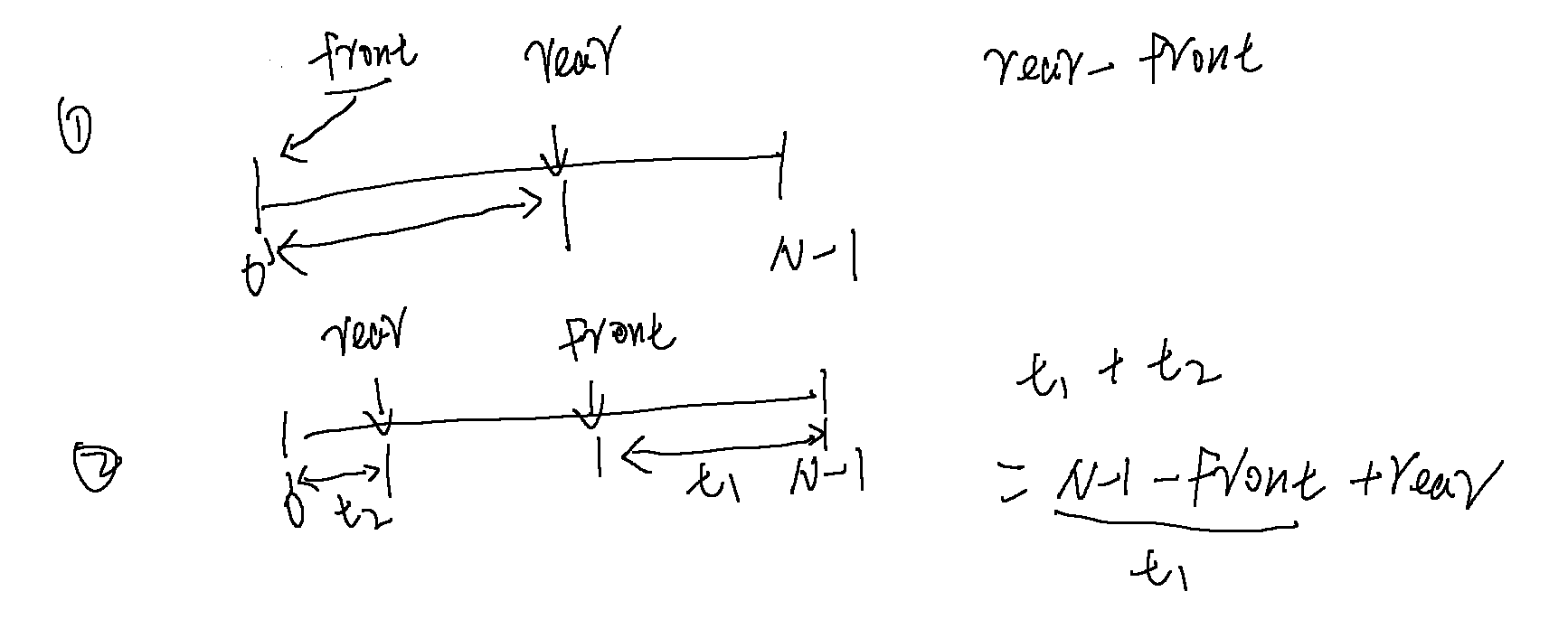
  • 计算队列元素个数

image-20221004152401680

  • 源文件
04-ds/18-double_sequeue_one_seqstack.c
  • 源代码
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// sequence queue

#define N 32
typedef struct
{
    int data[N];
    int front; // 队列的头  , 数组的下标
    int rear;  // 队列的尾  , 数组的下标
} sequeue_t;

// 空队列的概念是 : 队头等于队尾
// 为了区分空队 和满队 , 队列元素个数要比数组元素少一个
// 满队+1 等于空队
// 1 2 3 4 5
// f       f
// r

sequeue_t *create_empty_sequeue()
{
    sequeue_t *q = (sequeue_t *)malloc(sizeof(sequeue_t));
    memset(q->data, 0, sizeof(q->data));
    q->front = q->rear = N - 1; //指向数组最后一个元素
    return q;
}

int sequeue_is_empty(sequeue_t *q)
{
    return (q->front == q->rear);
}

int sequeue_is_full(sequeue_t *q)
{
    // 队尾 +1 == 队头 , 就是满队
    // 任何一个一个数对N求余 , 这个数的范围是  0 - N-1
    return ((q->rear + 1) % N == q->front);
}

int sequeue_is_size(sequeue_t *q)
{
    // 队尾减去队头就是元素的个数
    if (q->rear >= q->front) //
        return (q->rear - q->front);
    else
        return (N - q->front + q->rear);
}

int sequeue_enqueue(sequeue_t *q, int value)
{
    if (sequeue_is_full(q))
    {
        printf("队列已满");
        return -1;
    }
    q->rear = (q->rear + 1) % N; // 防止数组越界
    q->data[q->rear] = value;
    return 0;
}
int sequeue_dequeue(sequeue_t *q, int *pvalue)
{
    if (sequeue_is_empty(q))
    {
        printf("队列已空");
        return -1;
    }
    q->front = (q->front + 1) % N; // 防止数组越界
    *pvalue = q->data[q->front];
    return 0;
}

int seqstack_push(sequeue_t *q1, sequeue_t *q2, int value)
{
    sequeue_enqueue(q1, value); // 队列不满
    return 0;
}
int seqstack_pop(sequeue_t *q1, sequeue_t *q2, int *pvalue)
{
    int value;
    // q1 出队列只剩下一个元素
    // printf("sequeue_is_size(q1)=%d\n",sequeue_is_size(q1));
    while (sequeue_is_size(q1) > 1)
    {
        sequeue_dequeue(q1, &value) ; 
        sequeue_enqueue(q2, value);
    }

    // 把q1中的元素出队
    sequeue_dequeue(q1, pvalue);

    // 把q2中的所有元素出队到q1
    while (sequeue_is_size(q2) > 0)
    {
        sequeue_dequeue(q2, &value);
        sequeue_enqueue(q1, value);
    }
    return 0;
}

int main(int argc, char const *argv[])
{
    sequeue_t *Q1 = create_empty_sequeue();
    sequeue_t *Q2 = create_empty_sequeue();
    printf("入栈顺序:");
    for (int i = 0; i < 32; i++)
    {
        if (seqstack_push(Q1, Q2, i + 1) == 0) // 表示成功
        {
            printf("%d ", i + 1);
        }
    }
    printf("\n");

    printf("出栈顺序:");
    for (int i = 0, value; i < 32; i++)
    {
        if (seqstack_pop(Q1, Q2, &value) == 0)
        {
            printf("%d ", value);
        }
    }
    printf("\n");
    return 0;
}
  • 运行结果
入栈顺序:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 队列已满32 
出栈顺序:31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 队列已空1

4. 实例19 链式的双队列实现一个栈

  • 源文件
04-ds/19-double_linkqueue_one_linkstack.c
  • 源代码
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// link queue

typedef struct node
{
    int data;
    struct node *next;
} linklist_t;

typedef struct
{
    linklist_t *front; // 队头
    linklist_t *rear;  // 队尾
} linkqueue_t;

// 空队列的概念是 : 队头等于队尾
// 为了区分空队 和满队 , 队列元素个数要比数组元素少一个
// 满队+1 等于空队
// 1 2 3 4 5
// f       f
// r

linkqueue_t *create_empty_linkqueue()
{
    linklist_t *h = (linklist_t *)malloc(sizeof(linklist_t));
    linkqueue_t *q = (linkqueue_t *)malloc(sizeof(linkqueue_t));
    q->front = q->rear = h;
    q->front->data = 0;
    return q;
}

int linkqueue_is_empty(linkqueue_t *q)
{
    return (q->front == q->rear);
}


// 链式队列没有满的概念
// int linkqueue_is_full(linkqueue_t *q)
// {

// }

int linkqueue_is_size(linkqueue_t *q)
{
    int size = 0 ; 
    linklist_t *p = q->front->next;  // 指向队列的第1个元素
    while(p != NULL)
    {
        size ++; 
        p = p->next ; 
    }
    return size  ; 
}

// 入队 队尾加
int linkqueue_enqueue(linkqueue_t *q, int value)
{
    linklist_t *p = (linklist_t *)malloc(sizeof(linklist_t));
    p->data = value;
    p->next = q->rear->next; // 尾部插入第1步
    q->rear->next = p;       // 尾部插入第2步
    q->rear = p;             // 尾部插入第3步
    return 0;
}

// 头部出队列 , 头部删除法
int linkqueue_dequeue(linkqueue_t *q, int *pvalue)
{
    linklist_t *p;
    if (linkqueue_is_empty(q))
    {
        printf("队列为空");
        return -1;
    }
    p = q->front->next;           // 头节点的下一个节点  , p是要删除的节点
    q->front->next = p->next;     // 接上链表
    if (q->front->next == NULL) // 此时队列为空
        q->rear = q->front; // 
    
    *pvalue = p->data;
    free(p);
    return 0;
}

int linkstack_push(linkqueue_t *q1, linkqueue_t *q2, int value)
{
    linkqueue_enqueue(q1, value); // 队列不满
    return 0;
}
int linkstack_pop(linkqueue_t *q1, linkqueue_t *q2, int *pvalue)
{
    int value;
    // q1 出队列只剩下一个元素
    // printf("linkqueue_is_size(q1)=%d\n",linkqueue_is_size(q1));
    while (linkqueue_is_size(q1) > 1)
    {
        linkqueue_dequeue(q1, &value) ; 
        linkqueue_enqueue(q2, value);
    }

    // 把q1中的元素出队
    linkqueue_dequeue(q1, pvalue);

    // 把q2中的所有元素出队到q1
    while (linkqueue_is_size(q2) > 0)
    {
        linkqueue_dequeue(q2, &value);
        linkqueue_enqueue(q1, value);
    }
    return 0;
}

int main(int argc, char const *argv[])
{
    linkqueue_t *Q1 = create_empty_linkqueue();
    linkqueue_t *Q2 = create_empty_linkqueue();
    printf("入栈顺序:");
    for (int i = 0; i < 32; i++)
    {
        if (linkstack_push(Q1, Q2, i + 1) == 0) // 表示成功
        {
            printf("%d ", i + 1);
        }
    }
    printf("\n");

    printf("出栈顺序:");
    for (int i = 0, value; i < 32; i++)
    {
        if (linkstack_pop(Q1, Q2, &value) == 0)
        {
            printf("%d ", value);
        }
    }
    printf("\n");
    return 0;
}
  • 运行结果
入栈顺序:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 
出栈顺序:32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/21477.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

基于Labview的图像傅里叶变换研究-含Labview程序

基于Labview的图像傅里叶变换研究-含Labview程序

⭕⭕ 目 录 ⭕⭕一、说明二、基于Labview的图像傅里叶变换研究三、Labview源程序下载一、说明 订阅该专栏后&#xff0c;可获取该专栏内的任意一份代码&#xff0c;请及时私信博主获取下载链接。 从该专栏获取的程序&#xff0c;博主有责任并将保证该程序能在您电脑上完整运行…
阅读更多...
初识Spring框架~控制反转IoC、依赖注入DI以及Spring项目的创建方式

初识Spring框架~控制反转IoC、依赖注入DI以及Spring项目的创建方式

目录 Spring框架初识 Spring IoC IoC(控制反转) DI(依赖注入) Spring项目的创建 创建一个maven项目 配置XML文件 添加启动类 简单了解Bean对象的存储与获取 创建一个Spring IoC容器 注册Bean对象 获取并使用Bean对象 Spring框架初识 通常所说的Spring是指Spri…
阅读更多...
java知识梳理 第十五章 I/O流

java知识梳理 第十五章 I/O流

一、文件 1.1 文件流 值得一提的是&#xff0c;这里的流的概念是围绕java程序展开的 1.2 常用的文件操作 1.2.1 创建文件对象相关构造器和方法 代码演示如上&#xff0c;读者可自行实验 1.2.2 获取文件的相关信息 代码演示如上&#xff0c;读者可自行实验 1.2.3 目录的操作和删…
阅读更多...
NodeJs实战-待办列表(6)-前端绘制表格显示待办事项详情

NodeJs实战-待办列表(6)-前端绘制表格显示待办事项详情

NodeJs实战-待办列表6-前端绘制表格显示待办事项详情定义服务器返回的 json 数据前端绘制动态表格后端返回列表数据验证执行添加查看数据库中的数据是否与页面一致使用浏览器debug表格绘制过程项目地址前面几节显示的列表&#xff0c;看不到事项创建时间&#xff0c;完成时间&a…
阅读更多...
springmvc-day03

springmvc-day03

springmvc-day03 第一章 拦截器 1.概念 1.1 使用场景 1.1.1 生活中坐地铁的场景 为了提高乘车效率&#xff0c;在乘客进入站台前统一检票&#xff1a; 1.1.2 程序中的校验登录场景 在程序中&#xff0c;使用拦截器在请求到达具体 handler 方法前&#xff0c;统一执行检…
阅读更多...
基于stm32单片机的智能恒温自动加氧换水鱼缸

基于stm32单片机的智能恒温自动加氧换水鱼缸

资料编号&#xff1a;105 下面是相关功能视频演示&#xff1a; 105-基于stm32单片机的智能恒温自动加氧换水鱼缸Proteus仿真&#xff08;源码仿真全套资料&#xff09;功能讲解&#xff1a;采用stm32单片机&#xff0c;ds18b20测量温度&#xff0c;LCD1602显示温度&#xff0c…
阅读更多...
C语言第十一课(上)：编写扫雷游戏（综合练习2）

C语言第十一课(上)：编写扫雷游戏（综合练习2）

目录 前言&#xff1a; 一、文件建立&#xff1a; 1.头文件game.h&#xff1a; 2.函数定义文件game.c&#xff1a; 3.工程测试文件test.c&#xff1a; 二、编写井字棋游戏&#xff1a; 1.程序整体执行思路&#xff1a; 2.menu菜单&#xff1a; 3.game游戏函数逻辑&#xff…
阅读更多...
【Detectron2】代码库学习-5.标注格式- 矩形框， 旋转框，关键点， mask， 实例标注，IOU计算， 旋转框IOU计算，

【Detectron2】代码库学习-5.标注格式- 矩形框， 旋转框，关键点， mask， 实例标注，IOU计算， 旋转框IOU计算，

文章目录Detectron2 内置的标注格式BoxMode 表示方式实用APIRotatedBoxesInstances 实例标注KeypointsMasks结语Detectron2 内置的标注格式 BoxesRotatedBoxesBitMasksPolygonMasksROIMasksKeypointsInstancesImageList BoxMode 表示方式 XYXY_ABSXYWH_ABSXYXY_REL # 相对模…
阅读更多...
Windows安装mysql并且配置odbc

Windows安装mysql并且配置odbc

文章目录 mysql下载ODBC驱动下载安装mysql使用测试安装ODBC驱动添加ODBC数据源配置完成了用户不能远程访问的问题mysql下载 https://dev.mysql.com/downloads/installer/ ODBC驱动下载 https://dev.mysql.com/downloads/connector/odbc/ 安装mysql 点击mysql安装包，选择…
阅读更多...
【25-业务开发-基础业务-品牌管理-图片管理-图片上传方式的三种实现方式-第三方公共服务模块集成到项目中-服务端生成签名实战】

【25-业务开发-基础业务-品牌管理-图片管理-图片上传方式的三种实现方式-第三方公共服务模块集成到项目中-服务端生成签名实战】

一.知识回顾 【0.三高商城系统的专题专栏都帮你整理好了&#xff0c;请点击这里&#xff01;】 【1-系统架构演进过程】 【2-微服务系统架构需求】 【3-高性能、高并发、高可用的三高商城系统项目介绍】 【4-Linux云服务器上安装Docker】 【5-Docker安装部署MySQL和Redis服务】…
阅读更多...
【第三部分 | 移动端开发】1：移动端基础概要

【第三部分 | 移动端开发】1：移动端基础概要

目录 | 概述 | 手机端调试 | 视口 ViewPort 三种视口 meta标签 设置视口 代码适配PE端的要点 | 二倍图 物理像素和物理像素比 利用二倍图解决图片在PE端默认放大失真 背景缩放 background-size | 移动端的开发选择 | 移动端的相关开发注意点 | 概述 | 手机端调试 打…
阅读更多...
【操作系统习题】假定某多道程序设计系统供用户使用的主存空间为100 KB ，磁带机2台，打印机1台

【操作系统习题】假定某多道程序设计系统供用户使用的主存空间为100 KB ，磁带机2台，打印机1台

4&#xff0e;假定某多道程序设计系统供用户使用的主存空间为100 KB &#xff0c;磁带机2台&#xff0c;打印机1台。采用可变分区方式管理主存&#xff0c;采用静态分配方式分配磁带机和打印机&#xff0c;忽略用户作业I/O时间。现有如下作业序列&#xff0c;见表2-8。 采用先来…
阅读更多...
Linux磁盘分区中物理卷（PV）、卷组（VG）、逻辑卷（LV）创建和（LVM）管理

Linux磁盘分区中物理卷（PV）、卷组（VG）、逻辑卷（LV）创建和（LVM）管理

文章目录一 基础定义二 创建逻辑卷2-1 准备物理设备2-2 创建物理卷2-3 创建卷组2-4 创建逻辑卷2-5 创建文件系统并挂载文件三 扩展卷组和缩减卷组3-1 准备物理设备3-2 创建物理卷3-3 扩展卷组3-4 查看卷组的详细信息以验证3-5 缩减卷组四 扩展逻辑卷4-1 检查卷组是否有可用的空…
阅读更多...
Python实现全自动输入文本

Python实现全自动输入文本

文章目录1. 效果图2. 示例代码3. 代码解释1. 效果图 该Python脚本可以实现自动用Notepad打开文本文件&#xff0c;然后自动输入文本&#xff0c;最后保存并关闭文件&#xff0c;从而实现全面自动化处理文本。 2. 示例代码 Python脚本源码如下&#xff0c;主要使用了win32gui、…
阅读更多...
Modern Radar for Automotive Applications（用于汽车应用的现代雷达）

Modern Radar for Automotive Applications（用于汽车应用的现代雷达）

目录 1 引言 2 汽车雷达系统的工作原理 2.1 基本雷达功能 2.2 汽车雷达架构 2.2.1 发射机 2.2.2 接收机 2.2.3 天线和天线阵 2.3 信号模型 2.3.1 振幅模型 2.3.2 噪声模型 2.4 雷达波形和信号处理 2.4.1 距离处理 2.4.2 多普勒处理 2.4.3 FMCW汽车雷达应用的典型波形参数…
阅读更多...
[Unity好插件之PlayMaker]PlayMaker如何扩展额外创建更多的脚本

[Unity好插件之PlayMaker]PlayMaker如何扩展额外创建更多的脚本

学习目标&#xff1a; 如果你正在学习使用PlayMaker的话&#xff0c;那么本篇文章将非常的适用。关于如何连线则是你自己的想法。本篇侧重于扩展适用更多的PlayMaker行为Action&#xff0c;那么什么是PlayMaker行为Action呢&#xff1f; 就是这个列表。当我们要给PlayMaker行为…
阅读更多...
CSS的元素显示模式和CSS的背景

CSS的元素显示模式和CSS的背景

&#x1f353;个人主页&#xff1a;bit.. &#x1f352;系列专栏&#xff1a;Linux(Ubuntu)入门必看 C语言刷题 数据结构与算法 HTML和CSS3 目录 一.CSS的元素显示模式 1.1什么是元素的显示模式 1.2块元素 1.3行内元素 1.4 行内块元素 1.5元素显示模式总结 1.6…
阅读更多...
JavaEE——HttpServletRequest

JavaEE——HttpServletRequest

HttpServletRequest 核心方法 方法功能String getProtocol()返回请求协议的名称和版本。String getMethod()返回请求的 HTTP 方法的名称String getRequestURI()从协议名称直到 HTTP 请求的第一行的查询字符串中&#xff0c;返回该请求的 URL 的一部分。String getContextPath…
阅读更多...
DolphinScheduler3.1简介、部署、功能介绍以及架构设计

DolphinScheduler3.1简介、部署、功能介绍以及架构设计

DolphinScheduler3.1简介、部署、功能介绍以及架构设计1.DolphinScheduler简介 1-1.关于DolphinScheduler Apache DolphinScheduler 是一个分布式易扩展的可视化DAG工作流任务调度开源系统。适用于企业级场景&#xff0c;提供了一个可视化操作任务、工作流和全生命周期数据处…
阅读更多...
Day08--自定义组件的数据监听器案例

Day08--自定义组件的数据监听器案例

1.案例效果&#xff1a; 我的操作&#xff1a; 1》新建一个组件test4 2》在app.json里面将test4设置为全局组件 3》在home.wxml里面是用这个test4组件。 4》在test4.js中编写代码&#xff1a;【需要的配置项都弄一下呗。】 *********************************************…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023