LeetCode从入门到超凡（一）枚举算法

前言

大家好，我是GISer Liu😁，一名热爱AI技术的GIS开发者。本系列文章是我跟随DataWhale 2024年9月学习赛的LeetCode学习总结文档；本文主要讲解枚举算法。💕💕😊

一、基本概念

1.定义

定义：枚举算法通过**列举所有可能的解来找到满足条件的解**。它是一种“暴力搜索”方法，通过逐一检查每个可能的解，判断其是否满足问题的要求。
核心思想：枚举算法的核心思想是“穷举”，即通过系统地列举所有可能的情况，并逐一验证这些情况是否满足问题的条件。这种思想适用于那些解空间较小且可以预先确定的问题。

2. 优缺点

优点：
- 容易编程实现：枚举算法通常逻辑简单，易于编写和调试。
- 调试简单：由于算法逻辑清晰，调试过程中容易定位问题。
- 正确性容易证明：通过逐一验证所有可能的解，可以确保找到的解是正确的。
缺点：
- 效率较低：在大规模问题中，枚举所有可能的解会导致计算量巨大，效率低下。
- 空间复杂度高：在某些情况下，枚举算法可能需要大量的存储空间来存储所有可能的解。

3.适用场景

问题规模较小：当问题的规模较小，枚举所有可能的解不会导致计算量过大时，枚举算法是一个有效的选择。
问题解空间有限：当问题的解空间有限且可以预先确定时，枚举算法可以有效地找到所有满足条件的解。
需要验证所有可能的解：当需要确保找到所有可能的解，或者问题的解空间较小且易于列举时，枚举算法是一个合适的选择。

二、解题思路

思路

① 确定枚举对象、范围和判断条件

确定枚举对象：
- 明确需要枚举的变量或对象：在解题过程中，首先需要明确哪些变量或对象是需要枚举的。例如，在寻找两个数的和等于某个目标值的问题中，需要枚举两个数。
确定枚举范围：
- 确定每个枚举对象的取值范围：在确定枚举对象后，需要明确每个枚举对象的取值范围。例如，如果枚举对象是整数，需要确定其最小值和最大值。
确定判断条件：
- 设定判断条件以筛选出满足要求的解：在枚举过程中，需要设定一个或多个判断条件，以筛选出满足问题的解。例如，判断两个数的和是否等于目标值。

② 列举并验证

逐一列举所有可能的情况，并验证是否满足问题的解：
- 列举所有可能的情况：根据确定的枚举对象和范围，列举所有可能的情况。
- 验证是否满足问题的解：对每个列举的情况，使用设定的判断条件进行验证，筛选出满足条件的解。

③ 提高效率

缩小问题状态空间的大小：
- 减少枚举对象的数量：通过分析问题的特性，减少需要枚举的对象数量，从而缩小状态空间的大小。
- 减少枚举对象的取值范围：通过设定合理的上下界，减少枚举对象的取值范围，从而提高效率。
加强约束条件，缩小枚举范围：
- 增加额外的约束条件：通过增加额外的约束条件，进一步缩小枚举范围，减少不必要的计算。
- 利用对称性或其他数学性质：通过利用问题的对称性或其他数学性质，减少需要枚举的情况。
利用问题特有性质，避免重复求解：
- 避免重复计算：通过记录已经计算过的结果，避免重复求解相同的情况。
- 利用问题的特有性质：通过分析问题的特有性质，减少需要枚举的情况，提高效率。例如对称性等。

案例：百钱买百鸡问题

① 问题描述

给定 100 块钱，要求买 100 只鸡。已知公鸡每只 5 块钱，母鸡每只 3 块钱，小鸡每 3 只 1 块钱。问公鸡、母鸡、小鸡各买了多少只？

② 解题思路

确定枚举对象、范围和判断条件：
- 枚举对象：公鸡、母鸡、小鸡的只数，分别用变量 x、y、z 表示。

③ 流程图

lct

④ 代码实现

class Solution:
    def buyChicken(self):
        for x in range(21):
            for y in range(34):
                z = 100 - x - y
                if z % 3 == 0 and 5 * x + 3 * y + z // 3 == 100:
                    print("公鸡 %s 只，母鸡 %s 只，小鸡 %s 只" % (x, y, z))

# 示例
solution = Solution()
solution.buyChicken()

输出示例：

公鸡 0 只，母鸡 25 只，小鸡 75 只
公鸡 4 只，母鸡 18 只，小鸡 78 只
公鸡 8 只，母鸡 11 只，小鸡 81 只
公鸡 12 只，母鸡 4 只，小鸡 84 只

三、题目案例

1.两数之和

1. 两数之和 - 力扣（LeetCode）

① 问题描述

给定一个整数数组 nums 和一个目标值 target，找出数组中两个数的和等于目标值的所有组合。

② 解题思路

确定枚举对象、范围和判断条件：
- 枚举对象：数组中的两个数 nums[i] 和 nums[j]。
- 枚举范围：i 和 j 的取值范围分别是 0 到 n-1，其中 n 是数组的长度。
- 判断条件：nums[i] + nums[j] == target。
列举并验证：
- 使用两层循环，外层循环遍历 i，内层循环遍历 j，逐一列举所有可能的数对 (nums[i], nums[j])。
- 对每个数对，验证其和是否等于目标值 target。
提高效率：
- 减少枚举对象的数量：通过设定 j 的起始值为 i+1，避免重复枚举相同的数对。
- 减少枚举对象的取值范围：通过设定合理的上下界，减少需要枚举的数对数量。

③ 流程图

在这里插入图片描述

④ 代码实现

class Solution(object):
    def twoSum(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[List[int]]
        """
        result = []
        n = len(nums)
        
        for i in range(n):
            for j in range(i + 1, n):
                if nums[i] + nums[j] == target:
                    result.extend([i, j])
                    return result  # 假设你只想要第一个匹配的结果
        
        return result

调用测试：

2. 计数质数

204. 计数质数 - 力扣（LeetCode）

① 问题描述

给定一个整数 n，统计小于 n 的所有质数的数量。

质数是大于 1 的自然数，除了 1 和它本身外，不能被其他自然数整除的数。

② 解题思路

枚举区间内的每一个数，判断其是否为质数：
- 对于每个数 i（从 2 到 n-1），判断其是否为质数。
- 判断质数的方法：从 2 到 sqrt(i) 之间的每个数，检查 i 是否能被整除。如果能被整除，则 i 不是质数；否则，i 是质数。
优化判断质数的方法以提高效率：
- 使用埃拉托斯特尼筛法（Sieve of Eratosthenes）来标记非质数，从而减少判断次数。
- 初始化一个布尔数组 is_prime，大小为 n，初始值为 True。将 is_prime[0] 和 is_prime[1] 设为 False（因为 0 和 1 不是质数）。
- 从 2 开始，将每个质数的倍数标记为 False。

③ 流程图

在这里插入图片描述

④ 代码实现

class Solution(object):
    def countPrimes(self, n):
        """
        :type n: int
        :rtype: int
        """
        if n < 2:
            return 0
        
        is_prime = [True] * n
        is_prime[0] = is_prime[1] = False
        
        for i in range(2, int(n**0.5) + 1):
            if is_prime[i]:
                for j in range(i*i, n, i):
                    is_prime[j] = False
        
        return sum(is_prime)

# 调用测试
solution = Solution()
print(solution.countPrimes(10))  # 输出: 4 (2, 3, 5, 7)

执行通过！

3. 统计平方和三元组的数目

1925. 统计平方和三元组的数目 - 力扣（LeetCode）

① 问题描述

给定一个整数 n，统计所有满足以下条件的三元组 (a, b, c) 的数量：

a, b, c 都是小于等于 n 的正整数。
a^2 + b^2 = c^2。

② 解题思路

枚举区间内的每一对数，判断其平方和是否为完全平方数：
- 对于每一对 (a, b)（从 1 到 n），计算 a^2 + b^2。
- 判断 a^2 + b^2 是否为完全平方数：计算 sqrt(a^2 + b^2)，并检查其平方是否等于 a^2 + b^2。
优化枚举范围以提高效率：
- 由于 c 必须小于等于 n，因此 a 和 b 的枚举范围可以缩小到 sqrt(n) 以内。

③ 流程图

在这里插入图片描述

④ 代码实现

import math

class Solution(object):
    def countTriples(self, n):
        """
        :type n: int
        :rtype: int
        """
        count = 0
        
        for a in range(1, n + 1):
            for b in range(a, n + 1):
                c_squared = a**2 + b**2
                c = int(math.sqrt(c_squared))
                if c <= n and c**2 == c_squared:
                    if a == b:
                        count += 1  # (a, b, c) 和 (b, a, c) 是同一个三元组
                    else:
                        count += 2  # (a, b, c) 和 (b, a, c) 是两个不同的三元组
        
        return count

运行通过！

4. 统计公因子数目

2427. 公因子的数目

① 问题描述

给定两个正整数 $a$ 和 $b$ 。

要求：返回 $a$ 和 $b$ 的公因子数目。

说明：

公因子：如果 $x$ 可以同时整除 $a$ 和 $b$ ，则认为 $x$ 是 $a$ 和 $b$ 的一个公因子。
$\le a, b \le 1000$ 。

示例：

示例 1：

输入：a = 12, b = 6
输出：4
解释：12 和 6 的公因子是 1、2、3、6。

示例 2：

输入：a = 25, b = 30
输出：2
解释：25 和 30 的公因子是 1、5。

② 解题思路

枚举法：
- 对于每个可能的因子 $x$ （从 1 到 min(a, b)），检查 $x$ 是否能同时整除 $a$ 和 $b$ 。
- 如果 $x$ 能同时整除 $a$ 和 $b$ ，则 $x$ 是 $a$ 和 $b$ 的一个公因子。
优化：
- 由于 $x$ 的最大值为 min(a, b)，因此枚举范围可以缩小到 min(a, b)。

③ 流程图

在这里插入图片描述

④ 代码实现

class Solution(object):
    def commonFactors(self, a, b):
        """
        :type a: int
        :type b: int
        :rtype: int
        """
        count = 0
        for x in range(1, min(a, b) + 1):
            if a % x == 0 and b % x == 0:
                count += 1
        return count

运行通过！

5. 和为s的连续正数序列

剑指 Offer 57 - II. 和为s的连续正数序列

① 问题描述

给定一个正整数 target。

要求：输出所有和为 target 的连续正整数序列（至少含有两个数）。序列中的数字由小到大排列，不同序列按照首个数字从小到大排列。

说明：

$\le target \le 10^5$ 。

示例：

示例 1：

输入：target = 9
输出：[[2,3,4],[4,5]]

示例 2：

输入：target = 15
输出：[[1,2,3,4,5],[4,5,6],[7,8]]

② 解题思路

滑动窗口法：
- 使用两个指针 left 和 right 表示当前窗口的左右边界。
- 计算当前窗口内数字的和 sum。
- 如果 sum 等于 target，则记录当前窗口的序列。
- 如果 sum 小于 target，则右移 right 指针扩大窗口。
- 如果 sum 大于 target，则右移 left 指针缩小窗口。
优化：
- 由于序列至少包含两个数，因此 left 的最大值为 target // 2。

③ 流程图

在这里插入图片描述

④ 代码实现

class Solution(object):
    def fileCombination(self, target):
        """
        :type target: int
        :rtype: List[List[int]]
        """
        result = []
        left, right = 1, 2
        
        while left < right:
            sum = (left + right) * (right - left + 1) // 2
            if sum == target:
                result.append(list(range(left, right + 1)))
                left += 1
            elif sum < target:
                right += 1
            else:
                left += 1
        
        return result

运行通过！

6. 统计圆内格点数目

2249. 统计圆内格点数目

① 问题描述

给定一个二维整数数组 circles。其中 circles[i] = [xi, yi, ri] 表示网格上圆心为 (xi, yi) 且半径为 ri 的第 $ i $ 个圆。

要求：返回出现在至少一个圆内的格点数目。

说明：

格点：指的是整数坐标对应的点。
圆周上的点也被视为出现在圆内的点。
$\le circles.length \le 200$ 。
$c i rc l es [i] . l e n g t h == 3$ 。
$\le xi, yi \le 100$ 。
$\le ri \le min(xi, yi)$ 。
示例：
示例 1：

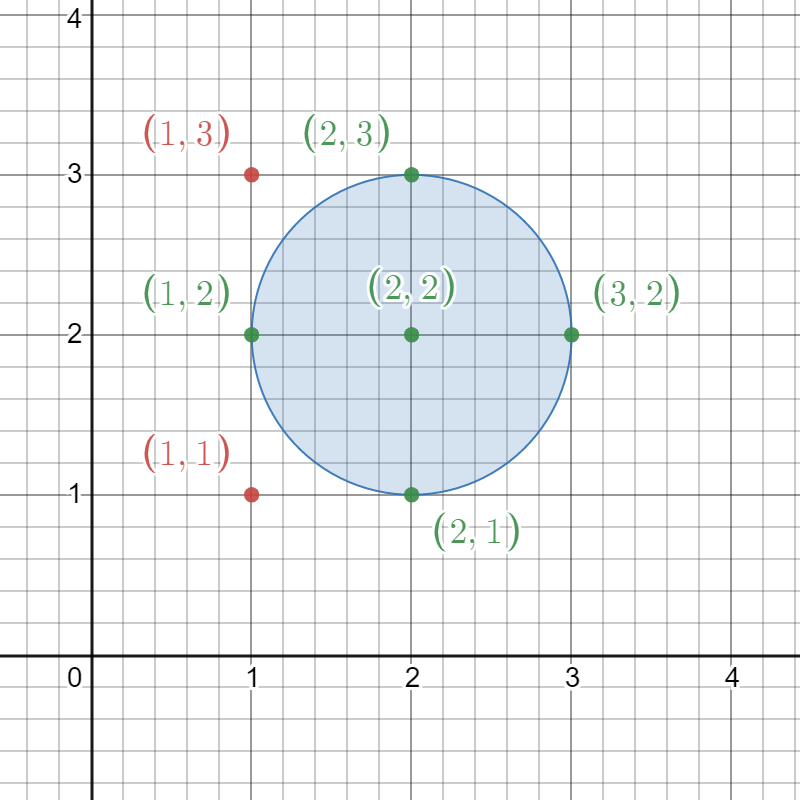
输入：circles = [[2,2,1]]
输出：5
解释：
给定的圆如上图所示。
出现在圆内的格点为 (1, 2)、(2, 1)、(2, 2)、(2, 3) 和 (3, 2)，在图中用绿色标识。
像 (1, 1) 和 (1, 3) 这样用红色标识的点，并未出现在圆内。
因此，出现在至少一个圆内的格点数目是 5。

示例 2：

输入：circles = [[2,2,2],[3,4,1]]
输出：16
解释：
给定的圆如上图所示。
共有 16 个格点出现在至少一个圆内。
其中部分点的坐标是 (0, 2)、(2, 0)、(2, 4)、(3, 2) 和 (4, 4)。

② 解题思路

枚举法：
- 对于每个圆，枚举其范围内的所有格点。
- 使用圆的方程 (x - xi)^2 + (y - yi)^2 <= ri^2 判断格点是否在圆内。
- 使用集合存储所有在圆内的格点，避免重复计数。
优化：
- 由于圆的半径最大为 100，因此格点的范围可以从 -100 到 200。

③ 流程图

在这里插入图片描述

④ 代码实现

class Solution(object):
    def countLatticePoints(self, circles):
        """
        :type circles: List[List[int]]
        :rtype: int
        """
        lattice_points = set()
        
        for circle in circles:
            xi, yi, ri = circle
            for x in range(xi - ri, xi + ri + 1):
                for y in range(yi - ri, yi + ri + 1):
                    if (x - xi) ** 2 + (y - yi) ** 2 <= ri ** 2:
                        lattice_points.add((x, y))
        
        return len(lattice_points)