目的是使用分布式的联合计算分发去替换掉区块链中原有的类第三方可信中心的证书机制，更加去中心化。

GS-TBK

Group Signatures with Time-bound Keys.

CS-TBK 算法

Complete subtree With Time-bound Keys，该算法是用来辅助检测用户的签名是否有效，是否在有效期内。

一些基本定义

+ $ T $：整个算法的最大的时间。 + $ BT $：一个完全二叉树 + $ t $ ：当前的时间。 + $ \tau $：有效时间，如果$ \tau

算法概述

首先每个叶子节点代表一个时间$ t $，可以理解为一个节点就是一个时间段。

算法输入是一个二叉树$ BT $和当前的时间$ t $，首先定义了两个空集合$ X，Y $，选取$ t-1 $这个叶子节点（如果$ t $是第一个节点，那么就选取$ t $这个节点），将对应的$ Path(\eta) $存到$ X $中，然后对于每个$ X $中的节点，将其不属于$ X $的右子节点存入$ Y $中，如果$ Y $为空，那么放入根节点，最后输出$ Y $。

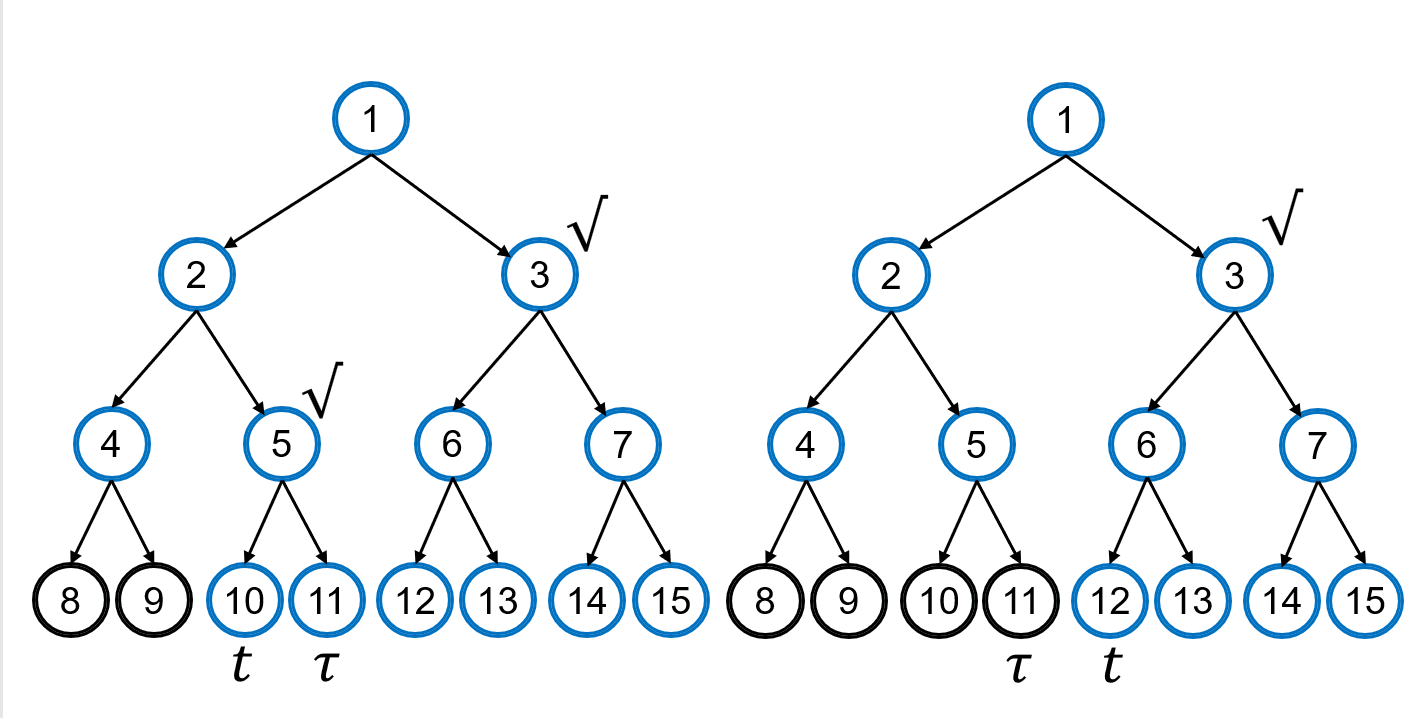
那么这个算法相当于对于当前的时间$ t $节点，会存在一个集合$ Y $，其中包括了不含$ Path(\eta) $的右子树节点。如下图，

若叶子节点8为例，那么$ X=Path(8)={1,2,4,8} $，$ Y={1} $（第一个节点）

若叶子节点10为例，那么$ X=Path(9)={1,2,4,9} $，$ Y={3,5} $

若叶子节点11为例，那么$ X=Path(10)={1,2,5,10} $，$ Y={3,11} $

若叶子节点12为例，那么$ X=Path(11)={1,2,5,11} $，$ Y={3} $

每个时间$ t $都将被分配到一个叶子节点（每个叶子节点代表一个时间），同样一个有效时间$ \tau $也会被分配到一个叶子节点。而一个用户会被分配到一个有效期$ \tau $。那么意味着，如果多个用户的$ \tau
$是相同的话，那么他们将会同时被分配到同一个叶节点。

在GS-TBK的应用-用户撤销管理

主要是管理用户的撤销。

$ GS-TBK $中所有的时间信息都交给一颗拥有最大数量$ T $叶节点的二叉树管理，有效期$ \tau $和当前时间$ t $都会和一个叶子节点绑定在一起。

如果$ \tau $分配到了节点$ \eta $，那么管理员将生成包含所有$ Path(\eta) $节点的签名，这些签名会发送给有效期是$ \tau $的用户（BTW，每个用户拿到的是不一样的，即便是同一个$ \tau $下的用户，但都包含同样的节点的信息）。

我们说，当$ \tau <t $，那么代表和$ \tau $绑定的所有用户都被撤销了，失效了，i.e.，叶子节点左边的叶子节点都被撤销了，以右上图的$ 12 $节点为例，那么$ 8,9,10,12 $都被撤销了。

接着管理员将生成$ CS-TBK $算法的输出节点集合（也就是集合$ Y $）的一系列签名信息，并广播，这些信息称为$ ei_t $(ExpireInformation)，用于后续的用户验证。如果$ \tau>t $，那么相关联的用户前面拿到的签名里应该持有和$ ei_t $中至少一个相同的节点的信息。那么如何检测是否过期呢？

还是以上面的图为例，假设$ \tau = 11 $，左边的图为用户没有过期，右边的图则为过期。

• 先看未过期的图，首先假设$ T=10 $，首先那么关联到11节点的用户将收到来自管理员的$ Path(11)={1,2,5,11} $四个节点的签名。在左边图里，当前时间为$ t=10 $，所以8和9节点被自然撤销了，根据$ CS-TBK $算法，$ 3、5 $将被选择为$ Y $集合元素输出，所以$ ei_t $里会包括$ 3、5 $的签名信息。此时，用户自己持有节点$ 5 $的签名即可证明自己的签名有效，没有过期。
• 再看右边的图，当前时间变为$ t=12 $，那么$ ei_t $里将只包括节点$ 3 $的签名，而节点$ 11 $关联的用户并不持有$ 3 $节点的签名，故，用户已经被撤销。

GS-TBK 方案

算法组成

1. $ GKeyGen(\lambda) $：输入安全参数，输出群公钥$ gpk $和私钥$ msk $。设定一个注册表$ reg $，最大有效期为$ T $（包含在gpk中）。 2. $ Join/Issue() $：用户与管理员之间的交互算法，用于给新加入的用户分发密钥和设置有效期。 + $ Join(gpk) $：输出用户的签名密钥$ gsk_i $，有效期$ \tau_i $，用户私钥$ usk_i $。 + $ Issue(msk,reg,\tau_i) $：输出$ reg $表，表中的每个元素都会存储$ grt_i $ (revocation token) 和有效期$ \tau_i $即，$ reg[i]=(grt_i,\tau_i) $。 3. $ Revoke(gpk,msk,t,reg,RU_t) $：$ RU_t $代表将要被撤销的用户集合，$ RL_t $（revocation list），设定其为空集合，如果$ \tau_i $过期了被提前撤销了，那么将对应的$ grt_{i,t} $存储到$ RL_t $中。然后算法计算$ ei_t $。最后输出$ RL_t $和$ ei_t $。 4. $ Sign(gpk,gsk_i,usk_i,m,t,ei_t) $：$ m $代表待签名的信息，最终输出签名$ \sigma $。 5. $ Verify(gpk,t,\sigma,m,RL_t) $：输出 valid or invalid 。 6. $ Open(gpk,msk,t,reg,\sigma,m,RL_t) $：输出用户的身份。

撤销方案

前面已经简单提过一下，现在具体描述一下。撤销主要分为自然撤销和提前撤销，前面描述的主要是自然撤销的一思路。

首先时间管理还是根据一颗二叉树，每一个节点都会跟一个域中的元素绑定，方便计算。

（这里不需要理解参数具体含义，知道有这个东西就好）

自然撤销

假定$ Path(\eta)=(u_!,\dots,u_l),u_l=\eta $，集合中的每个元素都是一个节点，它与一个域中的元素绑定在一起。

• 分发签名：前面说过，在用户分配到有效期$ \tau $之后，管理员会生成所有$ Path(\eta) $节点的签名并发送给用户，这个签名就是$ gsk_i = \left(\left{\left(A_{j}, \xi_{j}, \zeta_{j}\right), u_{i}\right}_{j \in[1, \ell]}\right) $，$ Path(\eta) $中有多少个节点就会有多少个$ A_j $，每个$ A_j $都存储了两个重要信息，即节点$ u $和用户自选的$ x $（包含在$ X $中）。
• 分发过期信息：在到达一个当前时间$ t $的时候，管理员会执行$ CS-TBK $，然后对结果计算签名，也就是过期信息$ ei_t $。假设$ CS-TBK $结果为$ Y = (v_1,\dots,v_{num}) $，那么计算的$ ei_t = \left{\left(B_{i, t}, \xi_{i}^{\prime}, \zeta_{i}^{\prime}\right)\right}_{i \in[1, \text { num }]} $，同样，$ Y $有多少个节点就会有多少个$ A_j $，每个$ A_j $都存储了两个重要信息，即节点信息$ v $和时间$ t $。
• 验证：在前面$ CS-TBK $的描述中已经说明，如果用户没有过期，也就是$ \tau>t $，$ \tau $在$ t $的右边，那么此时会存在一个节点$ u \in Path(\eta) \cap Y $，这个时候用户就可以通过零知识证明，证明自己的$ gsk_i $和$ ei_t $中存在相同节点。

提前撤销

实质是给被撤销的用户做了一个标识，后续通过验证签名来判定是否有效。

这里会涉及到一个椭圆双曲线映射，有如下图基本性质，

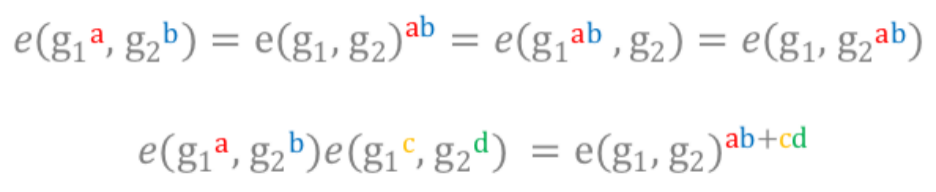
有三个群$ \mathbb{G}_1,\mathbb{G_2},\mathbb{G_t} $，满足$ \mathbb{G}_1 \times \mathbb{G_2} \rightarrow \mathbb{G_T} $，映射函数为$ e() $，$ \widetilde{g}，\widehat{g} $分别取自是$ \mathbb{G}_1,\mathbb{G_2} $。

提前撤销的用户将被提前存储在$ RU_t $中。然后会计算对应用户的$ grt_{i,t} $并放入$ RL_t $中，验证者通过依此检测$ RL_t $中的$ grt_{i,t} $是否满足映射关系来判定是否提前过期。具体如下，

在$ Join/Issue \ phase $ ，管理员存储了$ grt_i = \widetilde{X}_i = \widetilde{g}^{x_i=usk_i} \in \mathbb{G}_1 $，在到达时间$ t $的时候，管理员会计算一个$ \widetilde{h}_t = \widetilde{g}^{y_t} \in \mathbb{G}_1 $和$ \widehat{h}_t = \widehat{g}^{y_t}\in \mathbb{G}_2 $，此时会存在一个映射关系，即

$ e\left(\widetilde{h}{t}, \widehat{g}\right)=e\left(\widetilde{g}^{y{t}}, \widehat{g}\right)=e\left(\widetilde{g}, \widehat{g}^{y_{t}}\right)=e\left(\widetilde{g}, \widehat{h}_{t}\right) $。满足了，即可代表被撤销了。

在$ Sign \ phase $，产生的群签名$ \sigma $会包含$ \widetilde{h}t^{\beta,\widetilde{g}}{d(x_i+\beta)} $，假设某用户被提前撤销了，那么群管理员会计算$ grt{i,t} = grt_i^{{y_t}=\widetilde{h}_t}{x_i} $，然后将它存到$ RL_t $中，此时的$ grt_{i,t} $会满足一个映射关系，即

$ e(grt_{i,t}\widetilde{h}{t}^{{\beta},\widehat{g}}{d})=e(\widetilde{h}{t}^{{x_{i}+\beta},\widehat{g}}{d})=e(\widetilde{g}^{{y_{t}(x_{i}+\beta)},\widehat{g}}{d})=e(\widetilde{g}^{{d(x_i+\beta)},\widehat{g}}{y_t})=e(\widetilde{g}^{d(x_i+\beta)},\widehat{h}_t) $

验证者通过检测是否满足上面等式来判定该用户的签名是否过期，满足则用户存在于撤销名单中，则签名无效。

分布式GS-TBK 思路

方案中加入了一个代理节点，用于减少通信的开销。

（以下表述中，委员会 = 管理员= Node，代理 = Proxy， 用户 = User）

Setup Phase

方案思路

这个阶段主要是信息的初始化以及连接的建立。

• 代理 Proxy
  1. 代理节点初始化自己的信息（门限信息，通信连接信息等），生成树。
• 委员会 Node
  1. 委员会节点初始化自己的信息（包含生成 CL 同态密钥对，通信连接信息，门限信息等等），接着所有委员会节点会将自己的同态公钥P2P发给代理服务器，然后代理服务器会对其进行排序，然后返回给委员会公钥集合以及相应的序号，便于节点建立连接

代码思路

1. Proxy 加载自己的配置完成初始化，生成树，并为叶子节点分配时间，设定有效期，开启监听，等待节点连接。 2. 所有 Nodes 加载自己的配置完成初始化，然后与 Proxy 建立连接，连接后**P2P**发送自己的PK和监听地址给Proxy。 3. Proxy 收到所有的 PK 后，对其排序，然后返回一个 NodeInfo list，包含参与的Node id，监听地址和PK，同时还将发送生成好的tree信息，广播给所有的 Nodes。 4. 所有Nodes根据收到的NodeInfo list 和对应的 Node 建立 p2p 连接，完成信道搭建。信道搭建好后将句柄和对应id号存储下来，便于消息的发送。 5. 所有Nodes发送阶段结束Flag，Proxy收到后也发送一个结束Flag。

GKeyGen Phase

方案思路

这个阶段主要需要生成公钥和四把私钥。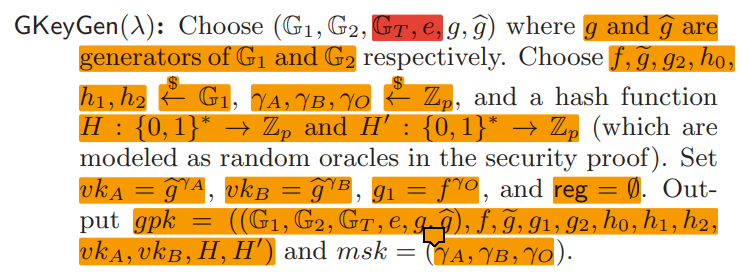

上面的图片是非分布式的方案原型，接下来将其拆解为分布式包含代理的版本。

主要的不同来自于四把私钥$ \gamma_A,\gamma_B,\gamma_O,\gamma_C $的生成，不是随机选取，而是通过分布式密钥生成（DKG）。最终的结果是每个委员会节点将持有四把私钥的分各自一部分碎片（$ (t,n) $share ）。

另外需要再加一把密钥$ \gamma_C $，此密钥和前面的三把密钥生成一样的，用于后面的 Open Phase 中公开用户的身份

公共参数：$ pp = ((G_1,G_2,G_T,e,g, \hat{g})，f, \tilde g, g_2, h_0, h_1, h_2 \leftarrow \mathbb{Z}_q,H,H’)
$

联合计算参数： $ (\gamma_A, \gamma_B, \gamma_O, \gamma_C) \leftarrow DKG(pp, n, t, CL_{PK}, s) $

Phase one

• 代理 Proxy
  1. 广播发送给委员会节点阶段开始flag信息。
  2. 计算出$ GPK $中除了$ vk_A = \hat g^{\gamma_A},vk_B = \hat g^{{\gamma_B},g_1=f}{\gamma_O} $的部分，并选择出参与节点。
  3. 然后一并广播发送给委员会节点
• 委员会 Node
  1. 收到flag后，也P2P对代理发送一个阶段开始Flag信息。
  2. 每个委员会节点自选随机数作为私钥$ u_i $，然后计算自己的公钥$ y_i=g^{u_i} $，并对该公钥做一个哈希承诺，
  3. 在整个委员会集体里进行广播该承诺。

---

Phase two

• 委员会 Node
  1. 每个委员会节点会收集上一轮所有的广播信息，进行承诺验证
  2. 计算出整体多项式的公钥$ y=\prod y_i $
  3. 接着根据自己自选的$ a_0 = u_i $进行FeldmanVss，生成多项式$ f_i(x)=a_o+a_1x+\dots a_{t-1}x^{t-1} $，
     1. 计算出多项式系数承诺$ c_{i_0}=g^{{a_0},c_{i_1}=g}{a_1},\cdots,c_{i_{t-1}}=g^{a_{t-1}} $
     2. 计算出对应节点的 $ (t,n) $share $ x_{ij}=f_i(j) $。
     3. 对委员会节点的share使用对应的 CL 公钥进行可验证加密得到$ CL_{Enc}(x_{ij}，pk_j) $，然后做零知识证明得到CLDLProof，该证明目的是证明CL密文中的$ x_{ij} $就是$ g^{x{ij}} $中的$ x_{ij} $。然后将 CL 密文和对应的 CLDLProof 发送给代理节点。
     4. P2P发给代理节点加密的 share，CLDLProof 和 多项式系数承诺。

---

Phase three

• 代理 Proxy
  1. 代理节点对收到的 CLDLProof 进行验证。
  2. 代理节点首先将收集到的多项式系数承诺进行合成，$ \prod c_{i_0},\prod c_{i_1},\dots \prod c_{i_{t-1}} $，得到整体多项式的系数承诺$ c_o,c_1,\dots,c_{t-1} $。
  3. 代理节点将收到的每个委员会节点的$ CL_{Enc}(x_{ij}，pk_j) $合成$ Enc(x_j)=CL_{Enc}(x_{j},pk_j) = \sum CL_{Enc}(x_{ij},pk_j) $.
  4. P2P发送给对应的委员会节点 合成的加密share 以及 合成的多项式承诺。

---

Phase four

• 委员会 Node
  1. 委员会节点解密收到的 $ x_j = CL_{Dec}(Enc(x_j),sk_j) $
  2. 委员会节点收到的$ x_j $的一致性进行验证，即$ g^{x_j}=g{S+a_1j+a_2{j^2} \cdots+a_t{j^{t-1}}} =c_0c_1^jc_2{j^2}\cdots c_t^{j{t-1}}
     $，
  3. 将最后的$ x_j $存储下来。

以上四个阶段称为一把密钥的分布式密钥生成（DKG）。

由于 **Gkeygen **有四把密钥所有，上述过程需要并行的执行四次，四次后每个节点得到私钥碎片$ \gamma_{A_i},\gamma_{B_i},\gamma_{O_i},\gamma_{C_i} $。

接下来是计算公钥 ****$ GPK $

---

Phase five

• 委员会 Node

委员会节点使用零知识证明，证明$ \hat g^{\gamma_{A_i}},\hat g^{{\gamma_{B_i}},f}{\gamma_{O_i}} $它们三个中的$ \gamma_{A_i}，\gamma_{B_i}，\gamma_{O_i} $和在前面的Phaseone中，委员会节点公开过三个$ g^{{\gamma_{A_i}},g}{\gamma_{B_i}},g^{\gamma_{O_i}} $中的三个相同

1. 具体方法是 委员会节点（Prover，P）和代理节点（Verifier，V）之间
    1. P 发送给 V $ \hat g^{\gamma_{A_i}},\hat g^{\gamma_{B_i}},f^{\gamma_{O_i}} $
    2. P 从域中任意选择一个$ t\in \mathbb{Z}_p $，计算$ g^t,\hat g^t,f^t $
    3. P 计算挑战$ e = Hash\{g,\hat g,f,g^{\gamma_{A_i}},g^{\gamma_{B_i}},g^{\gamma_{O_i}},\hat g^{\gamma_{A_i}},\hat g^{\gamma_{B_i}},f^{\gamma_{O_i}},g^t,\hat g^t,f^t\} $
    4. P 计算$ \begin{aligned}

z_{\gamma_{A_i}}=t+e\gamma_{A_i}\
z_{\gamma_{B_i}}=t+e\gamma_{B_i}\
z_{\gamma_{O_i}}=t+e\gamma_{O_i}
\end{aligned} $
5. P 发送给 V，proof: $ {g^t,\hat g^t,ft,e,z_{\gamma_{A_i}},z_{\gamma_{B_i}},z_{\gamma_{O_i}}} $
6. V 验证$ \begin{aligned}
g^z\stackrel{?}= g^t \cdot (g^{{\gamma_{A_i}})}e \
\hat g ^z\stackrel{?}= \hat g^t \cdot (\hat g^{{\gamma_{A_i}})}e
\end{aligned} $,$ \begin{aligned}
g^z\stackrel{?}= g^t \cdot (g^{{\gamma_{B_i}})}e \
\hat g ^z\stackrel{?}= \hat g^t \cdot (\hat g^{{\gamma_{B_i}})}e
\end{aligned} $，$ \begin{aligned}
g^z\stackrel{?}= g^t \cdot (g^{{\gamma_{O_i}})}e \
f ^z\stackrel{?}= f^t \cdot (f^{{\gamma_{O_i}})}e
\end{aligned} $

P2P发送给代理 proof 和$ \hat g^{\gamma_{A_i}},\hat g^{{\gamma_{B_i}},f}{\gamma_{O_i}} $。

• 代理 Proxy
  1. 验证ZKP，也就是前面的 f 步骤，然后聚合计算出$ \hat g^{\gamma_{A}}=\prod \hat g^{\gamma_{A_i}},\hat g^{\gamma_{B}}=\prod \hat g^{{\gamma_{B_i}},f}{\gamma_{O}}=\prod f^{\gamma_{O_i}} $，\ast \ast 广播\ast \ast 发送给委员会，然后自行组合出完整的$ GPK $。
  2. 广播给委员会

---

Phase six

• 委员会 Node
  1. 接收组合出完整的$ GPK $。

Join/Issue Phase


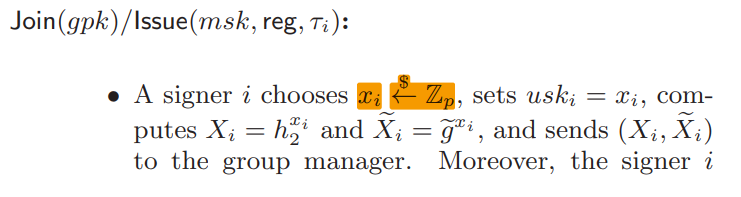
signer 对应的就是用户 User。这里需要计算出每个用户的$ gsk_i $由一组BBS签名和相关参数，然后管理员需要存储 Reg。

代码的demo实现里，达到了可以并发多个用户。

方案思路

**Phase one**

• 用户与代理建立连接，发送一个开始flag+自身ip
• 代理P2P发送公钥给用户

Phase two

• 用户 User
  1. 收到公钥后，用户初始化自己的信息（CL 同态密钥对，自选的私钥$ x_i $，和计算的公钥$ X_i,\tilde X_i $等等）
  2. 向代理节点提出申请，也就是P2P发送身份信息$ (pk,X_i,\tilde X) $和承诺信息
• 代理 Proxy
  1. 验证用户的承诺，如果通过，则再将承诺和身份信息$ \tau_i,grt_i $广播转发给参与委员会。
  2. 对每一个 Path 算法算出的树节点都计算出一个签名的底数$ Base = gh_{0}^{{\zeta_j}h_{1}}{u_j}X_i $然后保存。
• 参与委员会 Node
  1. 验证用户的承诺。
  2. 每个委员会参与节点之间开始初始化参数（选择随机数$ k_i,\xi_{j_i} $,生成MTA参数$ a,b $等）
     1. 进行 MTA 两两计算，最终每个节点将得到$ ni_{share}=(\xi_{j}+\gamma_A)k $ 的一部分（三轮）。
     2. 使用用户的CL公钥对$ k_i $进行加密得到$ C_{k_i}=CL_{Enc}(k_i,pk) $
     3. P2P发送给代理节点$ C_{k_i},pi_{share},\xi _{j_i} $

这里采用的是并行发送多个消息，避免多轮通信，后面的签名计算都是。

Phase three

• 代理 Proxy
  1. 合出$ (\xi_j+\gamma_A)k $，计算出$ A_j^{\frac 1 k}=Base^{\frac 1{(\xi_j+\gamma_A)k}} = gh_{0}^{{\zeta_j}h_{1}}{u_j}X_i ^{{\frac 1{(\xi_j+\gamma_A)k}}} $，
  2. 合出$ C_k = \sum C_{k_i} $
  3. 合出$ \xi_j = \sum \xi_{j_i} $,然后\ast \ast P2P\ast \ast 发送给用户$ A_j^{\frac 1 k},C_k,\xi_j,\zeta_j,u_j,\tau_i $。
  4. 广播给参与委员会$ A_j^{\frac 1 k} $

同样这里也不是一个而是多个，一组签名。

• 用户 User
  1. 解密$ k = CL_{Dec}(C_{k},sk) $，此时就可以计算出自己的签名$ A_j = (A_j^{\frac 1 k})^k $，然后合出自己的$ gsk_i $
• 参与委员会 Node
  1. 计算出$ A_j^{\frac {\gamma_{C_i}} k} $，然后P2P发送给代理。（一组）

---

Phase four

• 代理 Proxy
  1. 聚合出$ A_j^{\frac {\gamma_C} k}= \prod A_j^{\frac {\gamma_{C_i}} k} $，然后广播给参与委员会。（一组）

---

Phase five

• 参与委员会 Node
  1. 计算$ A_j^{\frac {\gamma_C \cdot k_i} k}=(A_j^{\frac {\gamma_C} k})k_i $（一组）
• 代理 Proxy
  1. 聚合出$ A_j^{\gamma_C}=\prod A_j^{\frac {\gamma_C \cdot k_i} k} $，然后广播发送给委员会。（一组）

---

Phase six

• 委员会 Node
  1. 存储下来到 Reg 中
  2. P2P 发送成功收下的flag给代理

Revoke Phase

方案思路


此步骤和 Join/Issue Phase 类似，但由于是公开的，所以无需加密。

$ ei_t $：这个是根据当前时间$ t $计算出来的一个用于后面校验签名有效性的信息。

$ RU_t $：存储的是在需要提前在$ t $时刻被撤销的用户列表，需要作为输入，提前生成。

$ RL_t $：存储的是$ grt_i $，表示的是在$ t $时刻被撤销的用户的信息，也需要提前置空。

Phase one

• 用户 User
  1. P2P发送给代理Revoke 的开始flag（）
• 代理 Proxy
  1. 收到用户flag和节点flag（需要收到这两个信息，这是为了保证多个用户同时执行的时候，消息异步到达引发的问题）后开始选择$ y_t $，计算$ \tilde h_t,\hat h_t $
  2. 选择当前时间$ t $和随机数$ \zeta_i’ $，对每一个CSTBK算法的树节点都计算出一个$ Base’ = gh_{0}^{{\zeta_i’}h_{1}}{v_i}h_2^t $，
  3. 广播发送这两个信息给参与委员会节点。
• 委员会 Node
  1. 每个委员会参与节点之间开始初始化参数（选择随机数$ k_i’,\xi_{i_j}’ $,生成MTA参数$ a,b $等）
     1. 进行 MTA 两两计算，最终每个节点将得到$ ni_{share}=(\xi_{i}'+\gamma_B)k $ 的一部分。
     2. P2P发送给代理节点$ ni_{share},k_i’,\xi_{i_j}’ $

Phase two

• 代理 Proxy
  1. 代理聚合出$ (\xi_i’+\gamma_B)k’ = \sum ni_{share} $, $ k’ = \sum k_i’ $, $ \xi_i’=\sum \xi_{i_j}’ $
  2. 然后计算出$ B_i = (Base’^{\frac 1 {(\xi_i’+\gamma_B)k’}})^{k’} = {gh_{0}^{{\zeta_i’}h_{1}}{v_i}h_2^t} {\frac 1 {(\xi_i’+\gamma_B)}} $
  3. 选出$ RU $并计算出$ RL $
  4. 广播给委员会节点
• 委员会 Node
  1. 存下$ ei_t，RL $
  2. P2P 发送成功收下的flag给代理
• 用户User
  1. 存下$ ei_t $

Sign Phase

方案思路


签名阶段就是用户拿着自己聚合出来的$ A_j $和$ Bi $对消息进行签名计算

主要就是几个式子的计算，和原方案一样。

保存下来， 然后上链。

结束后P2P发送签名结束的 flag 给代理

Verify Phase

方案思路


这里的验证也和原方案类似，校验的是密钥是否过期（自然撤销，主动撤销，密钥）

不用代理验证，仅让代理转发消息，然后验证交给管理员节点，不通过则需要启动 Open Phase 来揭示用户身份。

代码demo里，流程是代理收到，用户发送自己已经签名完成的flag，结合node发送过来的revoke flag，这两个flag，然后发送开始验证的flag给委员会节点，此时委员会节点就会去链上读取用户的上链信息。

Open Phase

方案思路


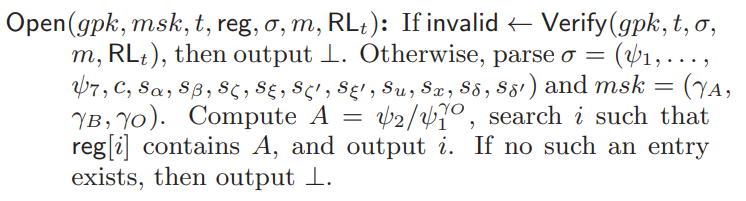这个阶段的改动比较大，主要是因为原方案里的 Open 是让委员会直接拿到的用户的签名$ A_j $的，修改的方案里是不能让其拿到，而是持有$ A_j^{\frac 1 k} $和$ A_j^{\gamma_C} $。

Phase one

• 委员会 Node
  1. 解析 Verify Phase 的结果，然后计算$ \psi_1^{\gamma_{O_i}} $，P2P发送给代理。
• 代理 Proxy
  1. 代理聚合$ \psi_1^{{\gamma_O}=\prod\psi_1}{\gamma_{O_i}} $，然后可以计算出$ A_j = \frac {\psi_2} {\psi_1^{\gamma_O}} $，然后广播给委员会节点

Phase two

• 委员会 Node
  1. 计算$ A_j^{\gamma_{C_i}} $，然后P2P发送给代理
• 代理 Proxy
  1. 代理聚合$ A_j^{\gamma_C}=\prod A_j^{\gamma_{C_i}} $，然后广播给委员会

Phase three

• 委员会 Node
  1. 寻找比对代理发送的$ A_j^{\gamma_C} $和自己的$ Reg $表中的信息，揭示出用户的身份信息。

Key manage Phase

方案思路

**转加法共享**

$ t $个委员会节点的 share，乘以对应的拉格朗日系数即可。

密钥恢复

$ t $个委员会节点联合进行恢复算法即可。实际上的方案是不需要恢复这个功能的，这里只是为了对生成的密钥进行验证

• 委员会 Node

将四把密钥的信息P2P发送给代理

• 代理 Proxy

对收到的信息进行聚合，然后运行恢复算法，再进行校验

密钥刷新

每个委员会节点将自选私钥设置为 0 ，然后重新生成多项式再次 Vss Share，最后累加到原来的$ (t,n) $share上即可 。过程类似 Keygen 的 Phase 2 ~ Phase 4

Phase one

• 代理 Proxy
  1. 发送给节点开始flag
• 委员会 Node
  1. 根据自己自选的$ a_0 = 0 $进行FeldmanVss，生成多项式$ f_i(x)=a_o+a_1x+\dots a_{t-1}x^{t-1} $
     1. 计算出多项式系数承诺$ c_{i_0}=g^{{a_0},c_{i_1}=g}{a_1},\cdots,c_{i_{t-1}}=g^{a_{t-1}} $
     2. 计算出对应节点的 $ (t,n) $share $ x_{ij}=f_i(j) $。
     3. 对委员会节点的share使用对应的 CL 公钥进行可验证加密得到$ CL_{Enc}(x_{ij}，pk_j) $，然后做零知识证明得到CLDLProof，该证明目的是证明CL密文中的$ x_{ij} $就是$ g^{x{ij}} $中的$ x_{ij} $。然后将 CL 密文和对应的 CLDLProof 发送给代理节点。
     4. P2P发给代理节点加密的 share，CLDLProof 和 多项式系数承诺。

一共四个

Phase two

• 代理 Proxy
  1. 代理节点对收到的 CLDLProof 进行验证。
  2. 代理节点首先将收集到的多项式系数承诺进行合成，$ \prod c_{i_0},\prod c_{i_1},\dots \prod c_{i_{t-1}} $，得到整体多项式的系数承诺$ c_o,c_1,\dots,c_{t-1} $。
  3. 代理节点将收到的每个委员会节点的$ CL_{Enc}(x_{ij}，pk_j) $合成$ Enc(x_j)=CL_{Enc}(x_{j},pk_j) = \sum CL_{Enc}(x_{ij},pk_j) $.
  4. P2P发送给对应的委员会节点 合成的加密share 以及 合成的多项式承诺。

Phase three

• 委员会 Node
  1. 委员会节点解密收到的 $ x_j = CL_{Dec}(Enc(x_j),sk_j) $
  2. 委员会节点收到的$ x_j $的一致性进行验证，即$ g^{x_j}=g{S+a_1j+a_2{j^2} \cdots+a_t{j^{t-1}}} =c_0c_1^jc_2{j^2}\cdots c_t^{j{t-1}}
     $
  3. 将最后的$ x_j $叠加到原来的 $ xj $上即可。