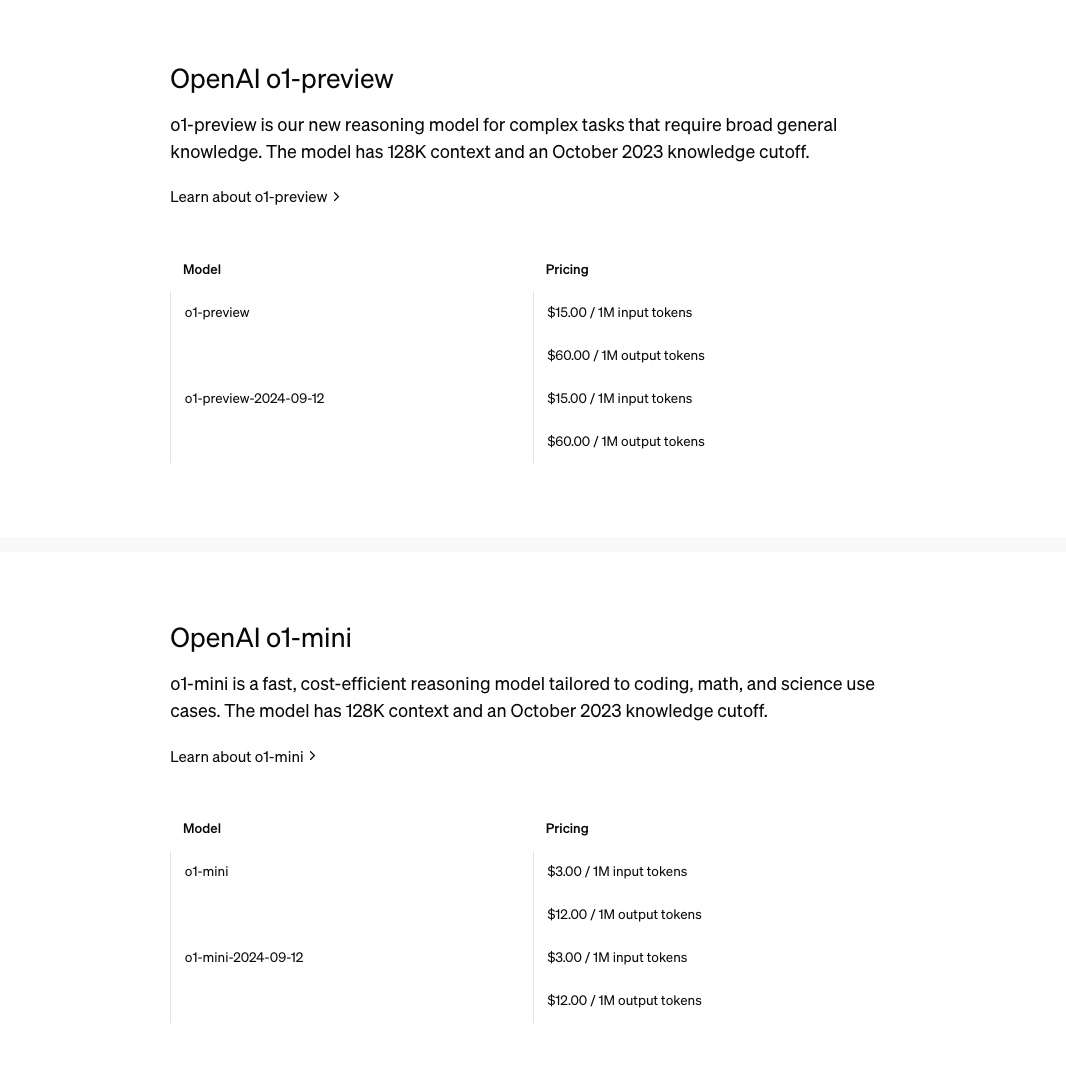
【题目】

CSP-J 2019 入门级 第一轮（初赛） 完善程序（1）
1.（矩阵变幻）有一个奇幻的矩阵，在不停的变幻，其变幻方式为：
数字 0 变成矩阵
0 0
0 1
数字 1 变成矩阵
1 1
1 0
最初该矩阵只有一个元素 0，变幻 n 次后，矩阵会变成什么样？
例如，矩阵最初为：[0]；
矩阵变幻 1 次后：
0 0
0 1
矩阵变幻 2 次后：
0 0 0 0
0 1 0 1
0 0 1 1
0 1 1 0
输入一行一个不超过 10 的正整数 n。输出变幻 n 次后的矩阵。
试补全程序。

#include <cstdio>
using namespace std;
int n;
const int max_size = 1 << 10;

int res[max_size][max_size];

void recursive(int x, int y, int n, int t) {
    if (n == 0) {
        res[x][y] = ①;
        return;
    }
    int step = 1 << (n - 1);
    recursive(②, n - 1, t);
    recursive(x, y + step, n - 1, t);
    recursive(x + step, y, n - 1, t);
    recursive(③, n - 1, !t);
}

int main() {
    scanf("%d", &n);
    recursive(0, 0, ④);
    int size = ⑤;
    for (int i = 0; i < size; i++) {
        for (int j = 0; j < size; j++)
            printf("%d", res[i][j]);
        puts("");
    }
    return 0;
}

1.①处应填（）
A. n%2
B. 0
C. t
D. 1

2.②处应填（）
A. x-step,y-step
B. x,y-step
C. x-step,y
D. x,y

3.③处应填（）
A. x-step,y-step
B. x+step,y+step
C. x-step,y
D. x,y-step

4.④处应填（）
A. n-1,n%2
B. n,0
C. n,n%2
D. n-1,0

5.⑤处应填（）
A. 1<<(n+1)
B. 1<<n
C. n+1
D. 1<<(n-1)

【题目考点】

1. 递归：求分形图

【解题思路】

观察可知，
变化0次，得到的矩阵为$1\ast 1$矩阵。
变化1次，得到的矩阵为$2\ast 2$矩阵。
变化2次，得到的矩阵为$4\ast 4$矩阵。
变化3次，得到的矩阵为$8\ast 8$矩阵。
…
变化n次，得到的矩阵为$2^n\ast 2^n$矩阵。

最后遍历输出时，行、列下标应该从0到$2^n-1$循环，所以size应该为$2^n$，1<<n的值就是$2^n$，第(5)空选B。

void recursive(int x, int y, int n, int t) {
    if (n == 0) {
        res[x][y] = ①;
        return;
    }
    int step = 1 << (n - 1);
    recursive(②, n - 1, t);
    recursive(x, y + step, n - 1, t);
    recursive(x + step, y, n - 1, t);
    recursive(③, n - 1, !t);
}

递归算法是将规模较大的问题分为几个与原问题形式类似但规模更小的子问题。
下面的几个递归调用就是在解决子问题。
首先step的值为$2^{n-1}$，这和主函数中的size的意义是相同的，表示当前子矩阵的行数和列数，因此第三个参数n指的是矩阵变换的次数。
要想得到当前变换n次后得到的矩阵，需要先得到4个变换n-1次后得到的矩阵。这四个子矩阵应该分别在变换n次后得到的矩阵的左上，左下，右上，右下四个方向的位置。
当n为0时，该矩阵为$1\ast 1$矩阵，只有一个元素，该元素的位置为x行y列，res[x][y]这一位置的值为空(1)要填的表达式。
空(1)的选项有：A. n%2，此时n为0，如果填n%2，那么每个位置的值都为0。如果填0或1，每个位置的值都相同。这与行列数大于1的矩阵中有0也有1相矛盾，因此res[x][y]的值只能是t，空(1)选C。
观察接下来的递归调用，有recursive(x, y + step, n - 1, t);，recursive(x + step, y, n - 1, t);，其中参数x、y的值分别为x, y+step与x+step, y。结合划分子矩阵的方案，可以知道，(x, y+step)是右上方子矩阵的左上角位置，(x+step, y)是左下方子矩阵的左上角的位置，因此第(2)空应该填左上方子矩阵左上角位置(x, y)，选D。第(3)空应该填右下方子矩阵的左上角位置(x+step, y+step) ，选B。

至于第4个参数t，当n为0时，t就是x，y位置的值。
当n>0时，t决定了该矩阵的形式。在当前题目的定义下，一个$2^n\ast 2^n$的矩阵的形式有两种，一种左上角为0，一种左上角为1。

比如n为1时，
左上角为0的矩阵为
0 0
0 1
左上角为1的矩阵为
1 1
1 0

将整个$2^n\ast 2^n$矩阵分成4个$2^{n-1}\ast 2^{n-1}$的矩阵，其中左上、右上、左下的子矩阵的左上角的值和整个矩阵左上角的值相同，只有右下方子矩阵左上角的值与整个矩阵左上角的值不同。
因此t表示的就是矩阵左上角的值。当前函数传入t，指的是当前矩阵左上角值为t，而后前三次递归调用传入的都是t，表示左上、右上、左下的子矩阵的左上角的值和整个矩阵左上角的值相同，第四题递归调用时传入的是!t，表示右下方子矩阵左上角的值与整个矩阵左上角的值不同。
所以主函数中调用recursive函数的写法为：recursive(0, 0, ④);，前两个参数是x和y，表示左上角位置为(0,0)，空(4)处需要填第3和第4个参数，矩阵需要变换n次，所以第三个参数填n。整个矩阵的左上角为0，所以第四个参数填0。第（4）空选B

【答案】

1. C
2. D
3. B
4. B
5. B