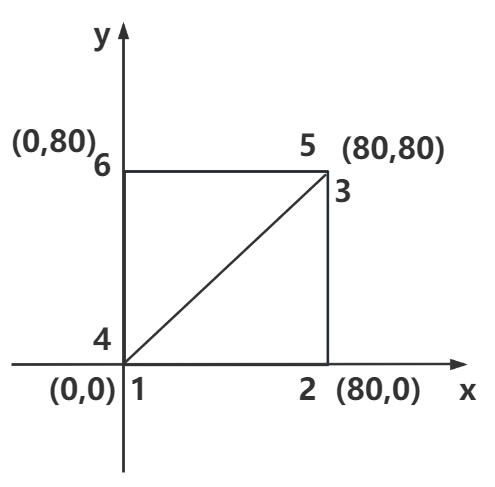
定义矩形几何体顶点坐标

一个矩形平面，可以至少通过两个三角形拼接而成。而且两个三角形有两个顶点的坐标是重合的。

注意三角形的正反面问题：保证矩形平面两个三角形的正面是一样的，也就是从一个方向观察，两个三角形都是逆时针或顺时针。

const vertices = new Float32Array([
    0, 0, 0, //顶点1坐标
    80, 0, 0, //顶点2坐标
    80, 80, 0, //顶点3坐标

    0, 0, 0, //顶点4坐标   和顶点1位置相同
    80, 80, 0, //顶点5坐标  和顶点3位置相同
    0, 80, 0, //顶点6坐标
]);