LC并联电路在正弦稳态下的传递函数推导(LC并联谐振选频电路)
本文通过 1.解微分方程、2.阻抗模型两种方法推导 LC 并联选频电路在正弦稳态条件下的传递函数,并通过仿真验证不同频率时 vo(t) 与 vi(t) 的幅值相角的关系。
电路介绍
已知条件
电路结构如下
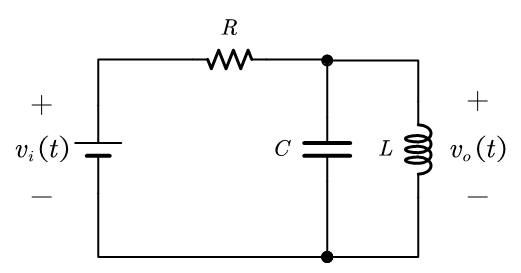
- R:电阻值
- C:电容值
- L:电感值
- 输入电源vi(t)
v i ( t ) = V I c o s ( w t ) v_i(t) = V_Icos(wt) vi(t)=VIcos(wt)
其中
V I :输入电压的幅值 w :输入电源的角频率 w 2 π :输入正弦信号的频率 \begin{array}{c} V_I: 输入电压的幅值\\ w: 输入电源的角频率\\ \frac{w}{2\pi} :输入正弦信号的频率 \end{array} VI:输入电压的幅值w:输入电源的角频率2πw:输入正弦信号的频率
理论计算
1.解微分方程法
解微分方程法常用的四个步骤
- 根据节点法列写微分方程
- 找出特解 vp(t)
- 找出对应的齐次方程的通解 vh(t)
- 根据初始条件计算通解中的常数参数
总的通解为特解+齐次解
v ( t ) = v p ( t ) + v h ( t ) v(t) = v_p(t) + v_h(t) v(t)=vp(t)+vh(t)
v p ( t ) v_{p}(t) vp(t) ,特解
v h ( t ) v_{h}(t) vh(t) ,齐次解
1.1 列些微分方程
前置知识
- 电容伏安特性: i = C d v d t i = C\frac{dv}{dt} i=Cdtdv
- 电感伏安特性: v = L d i d t v = L\frac{di}{dt} v=Ldtdi
- 电感伏安特性的积分形式:
1 L ∫ − ∞ t v d t = i \frac{1}{L} \begin{aligned} \int\limits_{-\infty}^t v \mathrm{d} t \end{aligned} = i L1−∞∫tvdt=i
节点法列方程
v i ( t ) − v o ( t ) R = C d v o ( t ) d t + 1 L ∫ − ∞ t v o ( t ) d t \frac{v_i(t) - v_o(t)}{R} = C\frac{dv_o(t)}{dt} + \frac{1}{L} \begin{aligned} \int\limits_{-\infty}^t v_o(t) \mathrm{d} t \end{aligned} Rvi(t)−vo(t)=Cdtdvo(t)+L1−∞∫tvo(t)dt
整理移相得
v i ( t ) R = C d v o ( t ) d t + 1 L ∫ − ∞ t v o ( t ) d t + v o ( t ) R \frac{v_i(t)}{R} = C\frac{dv_o(t)}{dt} + \frac{1}{L} \begin{aligned} \int\limits_{-\infty}^t v_o(t) \mathrm{d} t \end{aligned} +\frac{v_o(t)}{R} Rvi(t)=Cdtdvo(t)+L1−∞∫tvo(t)dt+Rvo(t)
等式两边对 t 微分,且带入 $
v_i(t) = V_Icos(wt)
$ 可得:
− w V I s i n ( w t ) R = C d v o 2 ( t ) d t 2 + 1 R d v o ( t ) d t + 1 L v o ( t ) \begin{array}{c} \frac{-wV_Isin(wt)}{R} = \\ C\frac{dv_o^2(t)}{dt^2} +\frac{1}{R}\frac{dv_o(t)}{dt} + \frac{1}{L}v_o(t) \end{array} R−wVIsin(wt)=Cdt2dvo2(t)+R1dtdvo(t)+L1vo(t)
1.2 找特解
设 vo(t) 的特解的形式为 v p ( t ) = A c o s ( w t + ϕ ) v_p(t) = Acos(wt+\phi) vp(t)=Acos(wt+ϕ),其中 A 和 ∅ 为要求得未知量,将 vp(t) 带入微分方程,可得:
− w V I s i n ( w t ) R = − C w 2 A c o s ( w t + ϕ ) − 1 R w A s i n ( w t + ϕ ) + 1 L A c o s ( w t + ϕ ) \begin{array}{c} \frac{-wV_Isin(wt)}{R} = -Cw^2Acos(wt+\phi) \\ -\frac{1}{R}wAsin(wt+\phi) + \frac{1}{L}Acos(wt+\phi) \end{array} R−wVIsin(wt)=−Cw2Acos(wt+ϕ)−R1wAsin(wt+ϕ)+L1Acos(wt+ϕ)
利用三角函数的公式可得:
− w V I s i n ( w t ) R = − C w 2 A c o s ( w t ) c o s ( ϕ ) + C w 2 A s i n ( w t ) s i n ( ϕ ) − w A R s i n ( w t ) c o s ( ϕ ) − w A R c o s ( w t ) s i n ( ϕ ) + A L c o s ( w t ) c o s ( ϕ ) − A L s i n ( w t ) s i n ( ϕ ) \begin{array}{c} \frac{-wV_Isin(wt)}{R} = -Cw^2Acos(wt)cos(\phi) + \\ Cw^2Asin(wt)sin(\phi)-\frac{wA}{R}sin(wt)cos(\phi) \\ -\frac{wA}{R}cos(wt)sin(\phi) + \frac{A}{L}cos(wt)cos(\phi)\\ -\frac{A}{L}sin(wt)sin(\phi) \end{array} R−wVIsin(wt)=−Cw2Acos(wt)cos(ϕ)+Cw2Asin(wt)sin(ϕ)−RwAsin(wt)cos(ϕ)−RwAcos(wt)sin(ϕ)+LAcos(wt)cos(ϕ)−LAsin(wt)sin(ϕ)
合并同类项
− w V I s i n ( w t ) R = ( A L − C w 2 A ) c o s ( w t ) c o s ( ϕ ) + ( C w 2 A − A L ) s i n ( w t ) s i n ( ϕ ) − w A R s i n ( w t ) c o s ( ϕ ) − w A R c o s ( w t ) s i n ( ϕ ) \begin{array}{c} \frac{-wV_Isin(wt)}{R} = \\ (\frac{A}{L}-Cw^2A)cos(wt)cos(\phi) + \\ (Cw^2A-\frac{A}{L})sin(wt)sin(\phi)-\\ \frac{wA}{R}sin(wt)cos(\phi) \\ -\frac{wA}{R}cos(wt)sin(\phi) \end{array} R−wVIsin(wt)=(LA−Cw2A)cos(wt)cos(ϕ)+(Cw2A−LA)sin(wt)sin(ϕ)−RwAsin(wt)cos(ϕ)−RwAcos(wt)sin(ϕ)
提公因式
− w V I s i n ( w t ) R = ( A L − C w 2 A ) ( c o s ( w t ) c o s ( ϕ ) − s i n ( w t ) s i n ( ϕ ) ) − w A R ( s i n ( w t ) c o s ( ϕ ) + c o s ( w t ) s i n ( ϕ ) ) \begin{array}{c} \frac{-wV_Isin(wt)}{R} = \\ (\frac{A}{L}-Cw^2A)(cos(wt)cos(\phi)\\ -sin(wt)sin(\phi))\\ -\frac{wA}{R}(sin(wt)cos(\phi) \\ +cos(wt)sin(\phi)) \end{array} R−wVIsin(wt)=(LA−Cw2A)(cos(wt)cos(ϕ)−sin(wt)sin(ϕ))−RwA(sin(wt)cos(ϕ)+cos(wt)sin(ϕ))
利用三角函数公式合并
− w V I s i n ( w t ) R = ( A L − C w 2 A ) c o s ( w t + ϕ ) − w A R s i n ( w t + ϕ ) \begin{array}{c} \frac{-wV_Isin(wt)}{R} = \\ (\frac{A}{L}-Cw^2A)cos(wt+\phi) \\ -\frac{wA}{R}sin(wt+\phi) \end{array} R−wVIsin(wt)=(LA−Cw2A)cos(wt+ϕ)−RwAsin(wt+ϕ)
根据以下公式
A 1 c o s ( θ ) − A 2 s i n ( θ ) = A 1 2 + A 2 2 s i n ( θ − t a n − 1 ( A 1 A 2 ) ) \begin{array}{c} A_1cos(\theta) - A_2sin(\theta)\\ =\sqrt{A_1^2+A_2^2}sin(\theta-tan^{-1}(\frac{A_1}{A_2})) \end{array} A1cos(θ)−A2sin(θ)=A12+A22sin(θ−tan−1(A2A1))
可以继续合并化简为:
− w V I s i n ( w t ) R = ( A L − C w 2 A ) 2 + ( w A R ) 2 ∗ s i n ( w t + ϕ − t a n − 1 ( A L − C w 2 A w A R ) ) \begin{array}{c} \frac{-wV_Isin(wt)}{R} = \\ \sqrt{(\frac{A}{L}-Cw^2A)^2+(\frac{wA}{R})^2}*\\ sin(wt+\phi-tan^{-1}(\frac{\frac{A}{L}-Cw^2A}{\frac{wA}{R}})) \end{array} R−wVIsin(wt)=(LA−Cw2A)2+(RwA)2∗sin(wt+ϕ−tan−1(RwALA−Cw2A))
令对应位置相等,可得
− w V I R = ( A L − C w 2 A ) 2 + ( w A R ) 2 \begin{array}{c} \frac{-wV_I}{R} = \sqrt{(\frac{A}{L}-Cw^2A)^2+(\frac{wA}{R})^2} \end{array} R−wVI=(LA−Cw2A)2+(RwA)2
ϕ = t a n − 1 ( R ( 1 − C w 2 L ) w L ) \begin{array}{c} \phi = tan^{-1}(\frac{R(1-Cw^2L)}{wL}) \end{array} ϕ=tan−1(wLR(1−Cw2L))
化简上式可得
( w V I ) 2 R 2 = ( A L − C w 2 A ) 2 + ( w A R ) 2 \begin{array}{c} \frac{(wV_I)^2}{R^2} = (\frac{A}{L}-Cw^2A)^2+(\frac{wA}{R})^2 \end{array} R2(wVI)2=(LA−Cw2A)2+(RwA)2
分解因式
( w V I ) 2 R 2 = A 2 L 2 + ( C w 2 A ) 2 − 2 A L C w 2 A + ( w A R ) 2 \begin{array}{c} \frac{(wV_I)^2}{R^2} = \\ \frac{A^2}{L^2}+(Cw^2A)^2-2\frac{A}{L}Cw^2A+(\frac{wA}{R})^2 \end{array} R2(wVI)2=L2A2+(Cw2A)2−2LACw2A+(RwA)2
两边同时乘以 L2R2
( L w V I ) 2 = A 2 R 2 + ( L R C w 2 A ) 2 − 2 A 2 L R 2 C w 2 + ( L w A ) 2 \begin{array}{c} (LwV_I)^2 = A^2R^2+(LRCw^2A)^2\\ -2A^2LR^2Cw^2+(LwA)^2 \end{array} (LwVI)2=A2R2+(LRCw2A)2−2A2LR2Cw2+(LwA)2
提出 A 移项整理得
A 2 = ( L w V I ) 2 R 2 + ( L R C w 2 ) 2 − 2 L R 2 C w 2 + ( L w ) 2 \begin{array}{c} A^2 = \frac{(LwV_I)^2}{R^2+(LRCw^2)^2 -2LR^2Cw^2+(Lw)^2} \end{array} A2=R2+(LRCw2)2−2LR2Cw2+(Lw)2(LwVI)2
分式上下同时除以 (Lw)2 得
A 2 = V I 2 ( R L w ) 2 + ( R C w ) 2 − 2 R 2 C L + 1 \begin{array}{c} A^2 = \frac{V_I^2}{(\frac{R}{Lw})^2+(RCw)^2-\frac{2R^2C}{L}+1} \end{array} A2=(LwR)2+(RCw)2−L2R2C+1VI2
两边开方,同时只取正解
A = V I ( R L w ) 2 + ( R C w ) 2 − 2 R 2 C L + 1 \begin{array}{c} A = \frac{V_I}{\sqrt{(\frac{R}{Lw})^2+(RCw)^2-\frac{2R^2C}{L}+1}} \end{array} A=(LwR)2+(RCw)2−L2R2C+1VI
因此,可得 vp 为
v p ( t ) = A c o s ( w t + ϕ ) v_p(t) = A cos(wt + \phi) vp(t)=Acos(wt+ϕ)
其中:
A = V I ( R L w ) 2 + ( R C w ) 2 − 2 R 2 C L + 1 \begin{array}{c} A = \frac{V_I}{\sqrt{(\frac{R}{Lw})^2+(RCw)^2-\frac{2R^2C}{L}+1}} \end{array} A=(LwR)2+(RCw)2−L2R2C+1VI
ϕ = t a n − 1 ( R ( 1 − C w 2 L ) w L ) \begin{array}{c} \phi = tan^{-1}(\frac{R(1-Cw^2L)}{wL}) \end{array} ϕ=tan−1(wLR(1−Cw2L))
1.3 找通解
微分方程对应的齐次方程为
0 = C d v o 2 ( t ) d t 2 + 1 R d v o ( t ) d t + 1 L v o ( t ) \begin{array}{c} 0 = C\frac{dv_o^2(t)}{dt^2} +\frac{1}{R}\frac{dv_o(t)}{dt} + \frac{1}{L}v_o(t) \end{array} 0=Cdt2dvo2(t)+R1dtdvo(t)+L1vo(t)
设齐次微分方程解的形式为
v h = A e s t \begin{array}{c} v_h = Ae^{st} \end{array} vh=Aest
其中 A 和 s 为待确定的参数,带入可得
0 = C A s 2 e s t + 1 R s A e s t + 1 L A e s t \begin{array}{c} 0 = CAs^2e^{st} + \frac{1}{R} sAe^{st} + \frac{1}{L}Ae^{st} \end{array} 0=CAs2est+R1sAest+L1Aest
不考虑 A 为 0 的情况,约掉同类项后可得
0 = C s 2 + 1 R s + 1 L \begin{array}{c} 0 = Cs^2 + \frac{1}{R} s + \frac{1}{L} \end{array} 0=Cs2+R1s+L1
解得
s 1 = − ( 1 R − 1 R 2 − 4 C L ) 2 C \begin{array}{c} s_1 = \frac{-(\frac{1}{R}-\sqrt{\frac{1}{R^2} - \frac{4C}{L}})}{2C} \end{array} s1=2C−(R1−R21−L4C)
s 2 = − ( 1 R + 1 R 2 − 4 C L ) 2 C \begin{array}{c} s_2 = \frac{-(\frac{1}{R}+\sqrt{\frac{1}{R^2} - \frac{4C}{L}})}{2C} \end{array} s2=2C−(R1+R21−L4C)
可得
v h = A 1 e s 1 t + A 2 e s 2 t \begin{array}{c} v_h = A_1e^{s_1t} + A_2e^{s_2t} \end{array} vh=A1es1t+A2es2t
因为 C > 0,L > 0,所以
( 1 R 2 − 4 C L ) < 1 R 2 \begin{array}{c} (\frac{1}{R^2} - \frac{4C}{L}) < \frac{1}{R^2} \end{array} (R21−L4C)<R21
所以
(
1
R
−
1
R
2
−
4
C
L
)
>
0
\begin{array}{c} (\frac{1}{R}-\sqrt{\frac{1}{R^2} - \frac{4C}{L}}) > 0 \end{array}
(R1−R21−L4C)>0
所以 s1 < 0,s2 < 0
同时,我们讨论的是正弦稳态的情况下的响应,所以 t 趋近于无限长,此时
A 1 e s 1 t → 0 , A 2 e s 2 t → 0 A_1e^{s_1t} \rightarrow 0,\qquad A_2e^{s_2t} \rightarrow 0 A1es1t→0,A2es2t→0
所以 vh = 0。
1.4 根据初始条件确定参数
由于稳态条件下通解为 0, 所以这一步不需要了。
1.5 最终的解
至此,用微分方程的方法得到的最终的解为
v o ( t ) = v p ( t ) + v h ( t ) v_o(t) = v_p(t) + v_h(t) vo(t)=vp(t)+vh(t)
即
v o ( t ) = A c o s ( w t + ϕ ) v_o(t) = A cos(wt + \phi) vo(t)=Acos(wt+ϕ)
其中:
A = V I ( R L w ) 2 + ( R C w ) 2 − 2 R 2 C L + 1 \begin{array}{c} A = \frac{V_I}{\sqrt{(\frac{R}{Lw})^2+(RCw)^2-\frac{2R^2C}{L}+1}} \end{array} A=(LwR)2+(RCw)2−L2R2C+1VI
ϕ = t a n − 1 ( R ( 1 − C w 2 L ) w L ) \begin{array}{c} \phi = tan^{-1}(\frac{R(1-Cw^2L)}{wL}) \end{array} ϕ=tan−1(wLR(1−Cw2L))
2.阻抗模型方法
阻抗模型下的电路示意图

2.1 基础知识
电阻的阻抗模型:
Z
R
=
R
Z_R = R
ZR=R
电容的阻抗模型:
Z C = 1 j w C Z_C = \frac{1}{jwC} ZC=jwC1
电感的阻抗模型:
Z L = j w L Z_L = jwL ZL=jwL
阻抗模型里,输入输出都是复数。
复数输入 Vi 为:
V i = V I e j w t V_i = V_Ie^{jwt} Vi=VIejwt
复数输出 Vo 为:
V o = V O e j w t + ϕ V_o = V_Oe^{jwt + \phi} Vo=VOejwt+ϕ
2.2 计算过程
阻抗模型的适用条件是正弦稳态条件下,可以直接利用分压法进行计算。
V o ( t ) = V i ( t ) Z C / / Z L Z R + Z C / / Z L V_o(t) = V_i(t) \frac{Z_C // Z_L}{Z_R + Z_C//Z_L} Vo(t)=Vi(t)ZR+ZC//ZLZC//ZL
其中
Z C / / Z L = 1 j w C + 1 j w L Z_C // Z_L = \frac{1}{jwC + \frac{1}{jwL}} ZC//ZL=jwC+jwL11
带入,可得
Z C / / Z L Z R + Z C / / Z L = 1 j w C + 1 j w L R + 1 j w C + 1 j w L \begin{array}{c} \frac{Z_C // Z_L}{Z_R + Z_C//Z_L} = \frac{\frac{1}{jwC + \frac{1}{jwL}}}{R+\frac{1}{jwC + \frac{1}{jwL}}} \end{array} ZR+ZC//ZLZC//ZL=R+jwC+jwL11jwC+jwL11
分子分母同时除以
1 j w C + 1 j w L \frac{1}{jwC + \frac{1}{jwL}} jwC+jwL11
可得
Z C / / Z L Z R + Z C / / Z L = 1 R ( j w C + 1 j w L ) + 1 \begin{array}{c} \frac{Z_C // Z_L}{Z_R + Z_C//Z_L} = \frac{1}{R(jwC+\frac{1}{jwL})+1} \end{array} ZR+ZC//ZLZC//ZL=R(jwC+jwL1)+11
继续化简
Z C / / Z L Z R + Z C / / Z L = 1 j ( R w C − R w L ) + 1 \begin{array}{c} \frac{Z_C // Z_L}{Z_R + Z_C//Z_L} = \frac{1}{j(RwC-\frac{R}{wL})+1} \end{array} ZR+ZC//ZLZC//ZL=j(RwC−wLR)+11
用复数的角坐标表示
Z C / / Z L Z R + Z C / / Z L = 1 1 + ( R w C − R w L ) 2 e j t a n − 1 ( R w C − R w L ) \begin{array}{c} \frac{Z_C // Z_L}{Z_R + Z_C//Z_L} = \frac{1}{\sqrt{1+(RwC-\frac{R}{wL})^2}e^{jtan^{-1}(RwC-\frac{R}{wL})}} \end{array} ZR+ZC//ZLZC//ZL=1+(RwC−wLR)2ejtan−1(RwC−wLR)1
拆分并化简倒数为负指数
Z
C
/
/
Z
L
Z
R
+
Z
C
/
/
Z
L
=
1
1
+
(
R
w
C
−
R
w
L
)
2
e
−
j
t
a
n
−
1
(
R
w
C
−
R
w
L
)
\begin{array}{c} \frac{Z_C // Z_L}{Z_R + Z_C//Z_L} = \frac{1}{\sqrt{1+(RwC-\frac{R}{wL})^2}} e^{-jtan^{-1}(RwC-\frac{R}{wL})} \end{array}
ZR+ZC//ZLZC//ZL=1+(RwC−wLR)21e−jtan−1(RwC−wLR)
将Vi(t),Vo(t)以及上边的传递函数带入
V o ( t ) = V i ( t ) Z C / / Z L Z R + Z C / / Z L \begin{array}{c} V_o(t) = V_i(t) \frac{Z_C // Z_L}{Z_R + Z_C//Z_L} \end{array} Vo(t)=Vi(t)ZR+ZC//ZLZC//ZL
可得
V O e j ( w t + ϕ ) = V I e j w t 1 1 + ( R w C − R w L ) 2 e − j t a n − 1 ( R w C − R w L ) \begin{array}{c} V_Oe^{j(wt + \phi)} = \\ V_Ie^{jwt}\frac{1}{\sqrt{1+(RwC-\frac{R}{wL})^2}} e^{-jtan^{-1}(RwC-\frac{R}{wL})} \end{array} VOej(wt+ϕ)=VIejwt1+(RwC−wLR)21e−jtan−1(RwC−wLR)
合并化简可得
V O e j ( w t + ϕ ) = V I 1 + ( R w C − R w L ) 2 e j ( w t − t a n − 1 ( R w C − R w L ) ) \begin{array}{c} V_Oe^{j(wt + \phi)} =\\ \frac{V_I}{\sqrt{1+(RwC-\frac{R}{wL})^2}} e^{j(wt-tan^{-1}(RwC-\frac{R}{wL}))} \end{array} VOej(wt+ϕ)=1+(RwC−wLR)2VIej(wt−tan−1(RwC−wLR))
取对应项相等,可得
V O = V I 1 + ( R w C − R w L ) 2 \begin{array}{c} V_O= \frac{V_I}{\sqrt{1+(RwC-\frac{R}{wL})^2}} \end{array} VO=1+(RwC−wLR)2VI
ϕ = − t a n − 1 ( R w C − R w L ) \phi =-tan^{-1}(RwC-\frac{R}{wL}) ϕ=−tan−1(RwC−wLR)
根据欧拉公式展开,并取虚部即为要求的时域部分的结果
v o ( t ) = V O c o s ( w t + ϕ ) v_o(t) = V_Ocos(wt+\phi) vo(t)=VOcos(wt+ϕ)
其中
V O = V I 1 + ( R w C − R w L ) 2 V_O= \frac{V_I}{\sqrt{1+(RwC-\frac{R}{wL})^2}} VO=1+(RwC−wLR)2VI
ϕ = − t a n − 1 ( R w C − R w L ) \phi =-tan^{-1}(RwC-\frac{R}{wL}) ϕ=−tan−1(RwC−wLR)
与微分方程计算的结果一致。
绘制函数曲线
传递函数
使用函数绘制工具,以 w 作为变量,绘制传递函数的曲线,并调整 L,R,C 参数,观察不同参数对传递函数的影响,绘制演示如下
下面视频是不同 w 下的幅值变化曲线,可以观察到改变 L 可以调整谐振频率,更改 C 既会影响谐振频率,又会改变通频带的胖瘦(品质因数 Q ),更改 R 只改变胖瘦(品质因数 Q ),不改变谐振频率,在谐振频率处传递函数的幅值为1,说明输出幅值与输入幅值相等。
LC并联电路传递函数幅值随w的变化
下面是不同 w 下的相角变化曲线,上下的角度是正负 90°,改变 R 不会改变谐振频率,在谐振频率相角为 0°。
LC并联电路相角随w的变化
通过曲线图可以看到,电阻会影响品质因数,但是不会改变谐振频率,谐振频率处的输出信号幅值与输入相等,相角偏移为0,说明谐振时,输出与输入完全一致。
谐振频率为:
F = 1 2 π L C F = \frac{1}{2\pi\sqrt{LC}} F=2πLC1
电路的品质因数 Q 为谐振频率 与 带宽的比值,带宽是幅值为幅值为谐振点幅值的 0.707 倍时的频率点的差值,因此,波形越瘦,电路的品质因数越高,改变电阻可以改变品质因数。
仿真验证
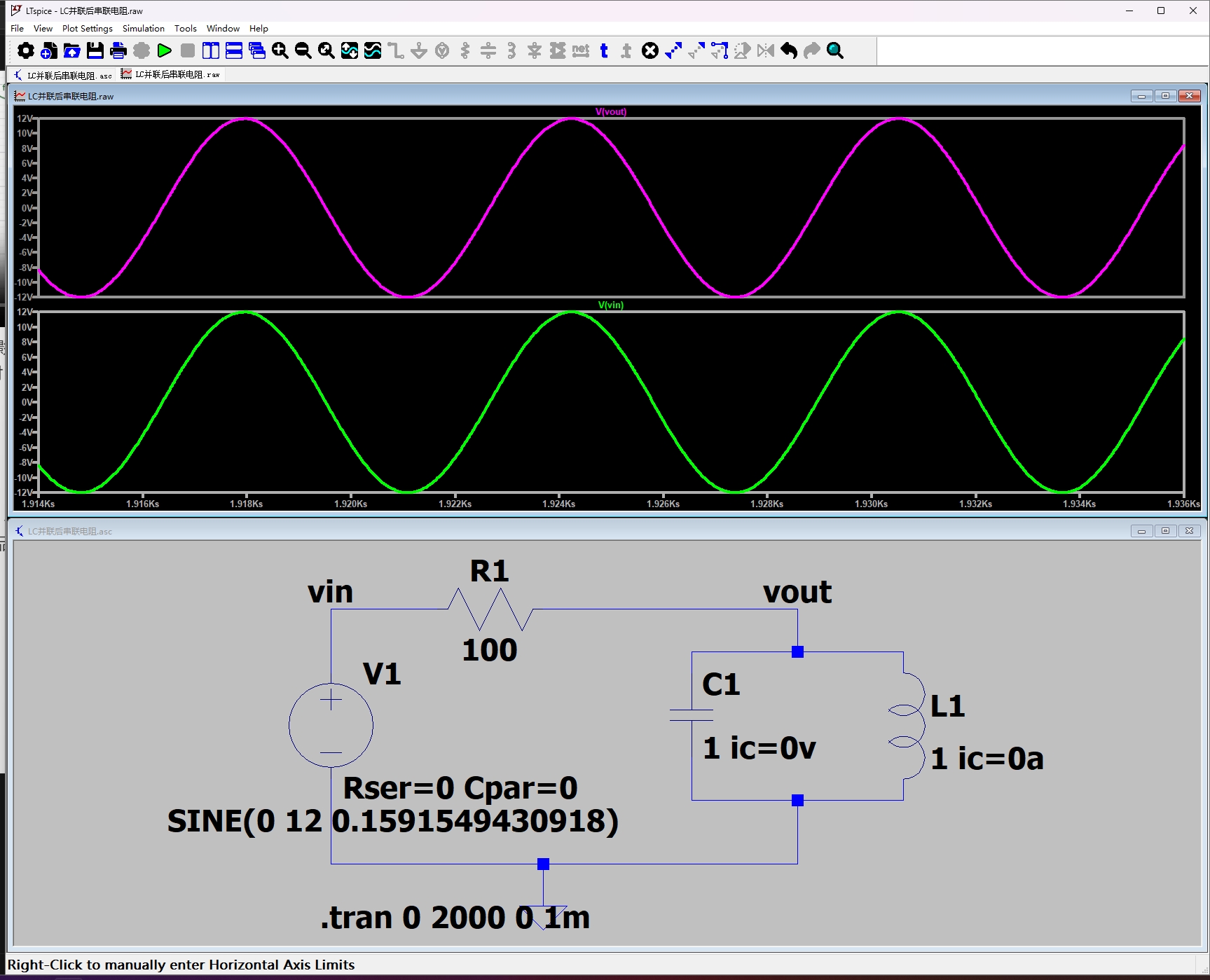
下图仿真在谐振点时输入信号与输出信号完全相同
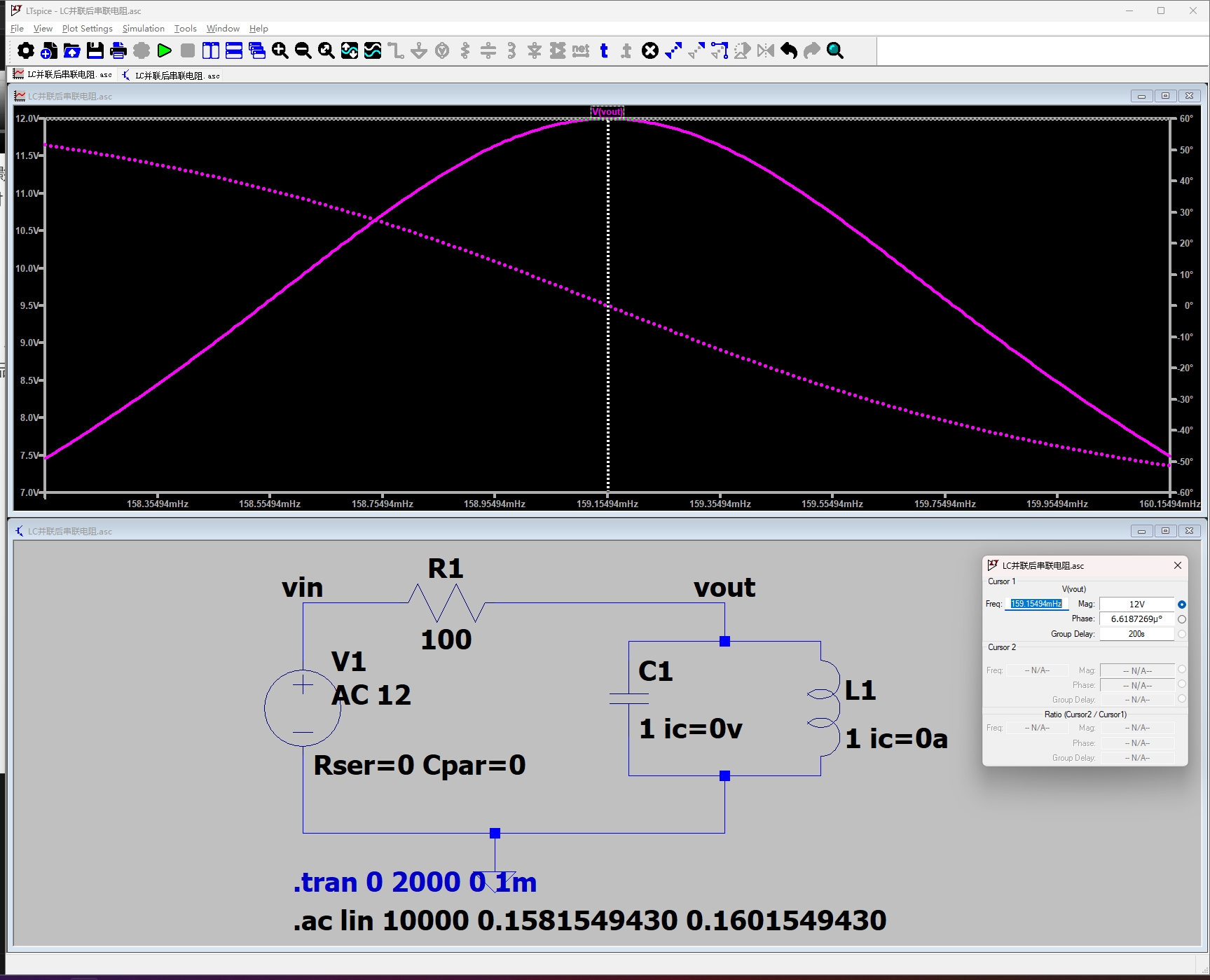
下图是扫频的仿真,可以看到,在谐振点处传递函数幅值最大为 1,且相角为0.
参考
正弦稳态:https://www.bilibili.com/video/BV1ts411v7Ep?p=17
阻抗模型:https://www.bilibili.com/video/BV1ts411v7Ep?p=19
电路的 Q 值: https://www.crystal-radio.eu/enlckring.htm#q