环形公交路线上有 n 个站，按次序从 0 到 n - 1 进行编号。我们已知每一对相邻公交站之间的距离，distance[i] 表示编号为 i 的车站和编号为 (i + 1) % n 的车站之间的距离。

环线上的公交车都可以按顺时针和逆时针的方向行驶。

返回乘客从出发点 start 到目的地 destination 之间的最短距离。

示例 1：

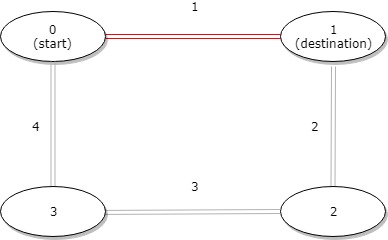
输入：distance = [1,2,3,4], start = 0, destination = 1
输出：1
解释：公交站 0 和 1 之间的距离是 1 或 9，最小值是 1。

示例 2：

输入：distance = [1,2,3,4], start = 0, destination = 2
输出：3
解释：公交站 0 和 2 之间的距离是 3 或 7，最小值是 3。

示例 3：

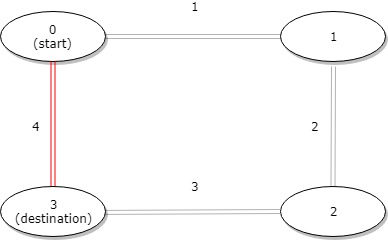
输入：distance = [1,2,3,4], start = 0, destination = 3
输出：4
解释：公交站 0 和 3 之间的距离是 6 或 4，最小值是 4。

思路

看到这题的第一眼，哇，简单题！今天又可以爽一把了，看了看题目，第一个想法是记录从起点正着走到终点的距离，然后在计算逆着从起点走到终点的距离，取最小值即可，但是觉得代码写起来好麻烦，于是突然意识到所有距离加起来不就是上面两次行走的距离之和了吗，既然逆着走比较麻烦那么我们只计算正着走的，然后遍历数组计算总路程，总路程减去正着走的路程就是逆着走的路程， 这道题很有意思，算是脑筋急转弯，想错了需要写一大堆代码才能解出来

解题过程

先遍历数组累加总路程，由于题目没有明确起点和终点哪个下标更大，我们取较小值为起点，较大值为终点，走一遍正序距离，然后比较正序距离和反序距离哪个更小返回即可

代码

class Solution {
    public int distanceBetweenBusStops(int[] distance, int start, int destination) {
        int res=0;
        int sum=0;

        for(int i=0;i<distance.length;i++){//计算总距离
            sum+=distance[i];
        }
        
        int s=Math.min(start,destination);
        int d=s==start?destination:start;

        for(int i=s;i<d;i++){//计算正序距离
            res+=distance[i];
        }
        return Math.min(res,sum-res);//返回较小值
    }
}