题目描述
定义两个相差为 2 的素数称为素数对,如 5 和 7,17 和 19 等,要求找出所有两个数均不大于 n 的素数对。
输入
一个正整数 n。1≤n≤10000。
输出
所有小于等于 n 的素数对。每对素数对输出一行,中间用单个空格隔开。若没有找到任何素数对,输出 empty。
样例输入1
10
样例输出1
3 5
5 7
样例输入2
100
样例输出2
3 5
5 7
11 13
17 19
29 31
41 43
59 61
71 73
样例输入3
3
样例输出3
empty
来源/分类(难度系数:4星)
函数与递归 数学思维
完整代码展示:
a=int(input())
def prime(i):
j=2
k=int(pow(i,0.5)) while j<=k:
if i%j==0:
break
j+=1
if j>k and i>=2:
return 1
s=[]
for i in range(2,a+1):
if prime(i)==1:
s.append(i)
x=[]
for i in range(0,len(s)-1):
k=s[i:i+2]
if k[0]+2==k[1]:
x.append(k)
if len(x)==0:
print("empty")
else:
for i in range(0,len(x)):
print(x[i][0],x[i][1])
a=int(input())
def prime(i):
j=2
k=int(pow(i,0.5))
while j<=k:
if i%j==0:
break
j+=1
if j>k and i>=2:
return 1
s=[]
for i in range(2,a+1):
if prime(i)==1:
s.append(i)
x=[]
for i in range(0,len(s)-1):
k=s[i:i+2]
if k[0]+2==k[1]:
x.append(k)
if len(x)==0:
print("empty")
else:
for i in range(0,len(x)):
print(x[i][0],x[i][1])
代码解释:
“a=int(input()) ”,让用户导入正整数a。
“def prime(i):
j=2
k=int(pow(i,0.5))
while j<=k:
if i%j==0:
break
j+=1
if j>k and i>=2:
return 1 ”,自定义一个函数prime(),用于判断函数中的实参i是否为素数:如果是,则返回值1。
“s=[]
for i in range(2,a+1):
if prime(i)==1:
s.append(i) ”,建立一个空列表s,将2~a中利用prime()函数判断为素数的数字依次添加进s中。
“x=[]
for i in range(0,len(s)-1):
k=s[i:i+2]
if k[0]+2==k[1]:
x.append(k) ”,建立一个空列表x,接着依次向右截取s中长度为2的列表片断k。并判断k[0]+2是否为k[1],如果是:则将k添加进x中。
“if len(x)==0:
print("empty")
else:
for i in range(0,len(x)):
print(x[i][0],x[i][1]) ”,判断列表x是否为空,如果是:则数出empty,否则依次输出x[i]中x[i][0],x[i][1]。
运行效果展示:
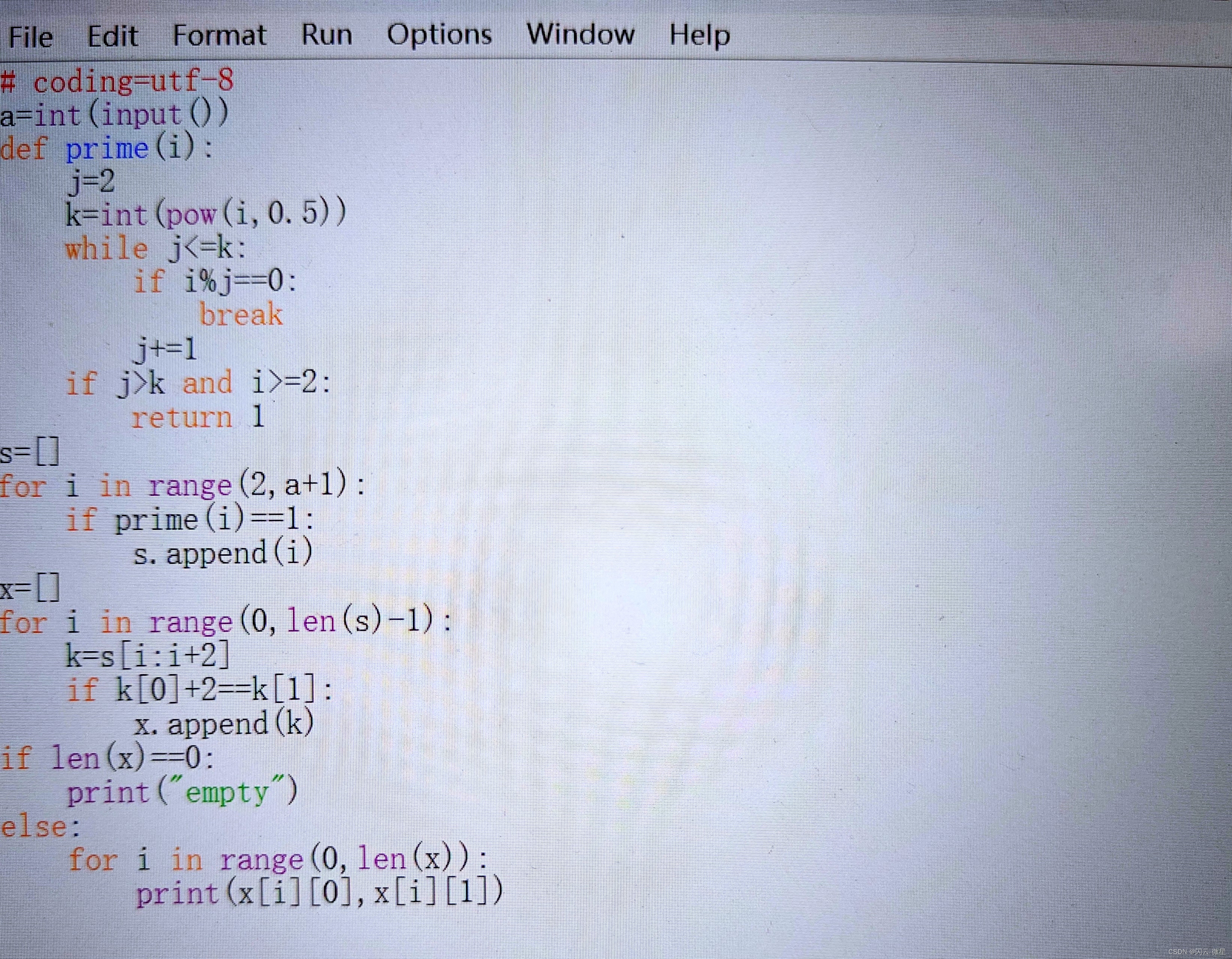

(声明:以上内容均为原创)













![【题解】【枚举】—— [USACO1.5] 回文质数 Prime Palindromes](https://i-blog.csdnimg.cn/direct/f782c1acde024adb925001c00e7952f4.jpeg#pic_center)





