目录
dijkstra(堆优化版)精讲
思路
堆优化细节
方法一: 最小堆优化
dijkstra(堆优化版)精讲
- 题目链接:卡码网:47. 参加科学大会
文章讲解:代码随想录
小明是一位科学家,他需要参加一场重要的国际科学大会,以展示自己的最新研究成果。
小明的起点是第一个车站,终点是最后一个车站。然而,途中的各个车站之间的道路状况、交通拥堵程度以及可能的自然因素(如天气变化)等不同,这些因素都会影响每条路径的通行时间。
小明希望能选择一条花费时间最少的路线,以确保他能够尽快到达目的地。
【输入描述】
第一行包含两个正整数,第一个正整数 N 表示一共有 N 个公共汽车站,第二个正整数 M 表示有 M 条公路。
接下来为 M 行,每行包括三个整数,S、E 和 V,代表了从 S 车站可以单向直达 E 车站,并且需要花费 V 单位的时间。
【输出描述】
输出一个整数,代表小明从起点到终点所花费的最小时间。
输入示例
7 9 1 2 1 1 3 4 2 3 2 2 4 5 3 4 2 4 5 3 2 6 4 5 7 4 6 7 9输出示例:12
【提示信息】
能够到达的情况:
如下图所示,起始车站为 1 号车站,终点车站为 7 号车站,绿色路线为最短的路线,路线总长度为 12,则输出 12。
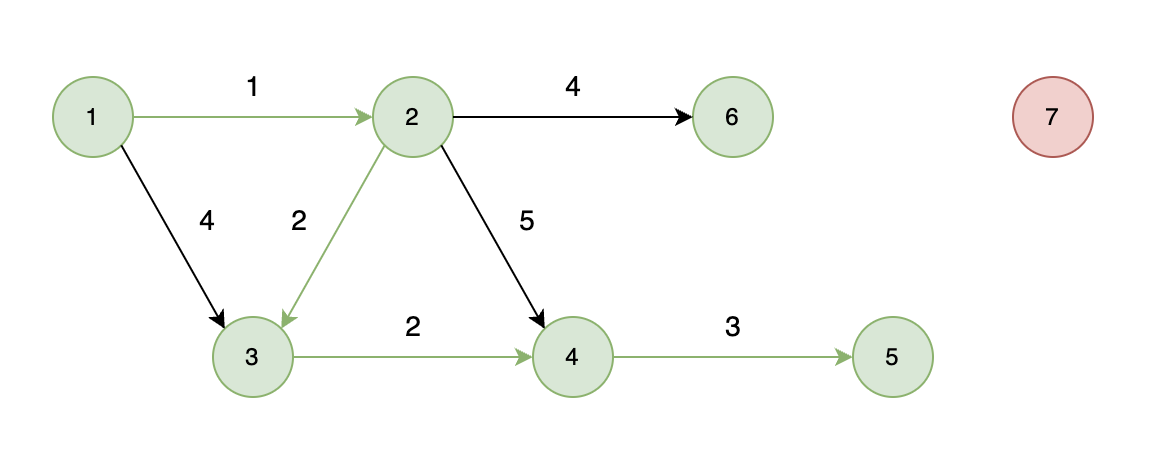
不能到达的情况:
如下图所示,当从起始车站不能到达终点车站时,则输出 -1。
数据范围:
1 <= N <= 500; 1 <= M <= 5000
思路
堆优化细节
其实思路依然是 dijkstra 三部曲:
- 第一步,选源点到哪个节点近且该节点未被访问过
- 第二步,该最近节点被标记访问过
- 第三步,更新非访问节点到源点的距离(即更新minDist数组)
只不过之前是 通过遍历节点来遍历边,通过两层for循环来寻找距离源点最近节点。 这次我们直接遍历边,且通过堆来对边进行排序,达到直接选择距离源点最近节点。
先来看一下针对这三部曲,如果用 堆来优化。
那么三部曲中的第一步(选源点到哪个节点近且该节点未被访问过),我们如何选?
我们要选择距离源点近的节点(即:该边的权值最小),所以 我们需要一个 小顶堆 来帮我们对边的权值排序,每次从小顶堆堆顶 取边就是权值最小的边。
(pq中中为什么要存 源点到该节点的权值,因为 这个小顶堆需要按照权值来排序)
有了小顶堆自动对边的权值排序,那我们只需要直接从 堆里取堆顶元素(小顶堆中,最小的权值在上面),就可以取到离源点最近的节点了 (未访问过的节点,不会加到堆里进行排序)
所以三部曲中的第一步,我们不用 for循环去遍历,直接取堆顶元素:
# 1. 第一步,选源点到哪个节点近且该节点未被访问过 (通过优先级队列来实现)
# 节点, 源点到该节点的距离
cur_dict,cur_node = heapq.heappop(pq)
第二步(该最近节点被标记访问过) 这个就是将 节点做访问标记,和 朴素dijkstra 一样 ,代码如下:
# 2. 第二步,该最近节点被标记访问过
visited[cur_node] = True
(cur.first 是指取 pair<int, int> 里的第一个int,即节点编号 )
第三步(更新非访问节点到源点的距离),这里的思路 也是 和朴素dijkstra一样的。
但很多录友对这里是最懵的,主要是因为两点:
- 没有理解透彻 dijkstra 的思路
- 没有理解 邻接表的表达方式
我们来回顾一下 朴素dijkstra 在这一步的代码和思路(如果没看过我讲解的朴素版dijkstra,这里会看不懂)
# 3、第三步,更新非访问节点到源点的距离(即更新minDist数组)
for j in range(1,n+1):
if not visited[j] and graph[cur][j] != float('inf') and graph[cur][j] + minDist[cur] < minDist[j]:
minDist[j] = minDist[cur] + graph[cur][j]其中 for循环是用来做什么的? 是为了 找到 节点cur 链接指向了哪些节点,因为使用邻接矩阵的表达方式 所以把所有节点遍历一遍。
而在邻接表中,我们可以以相对高效的方式知道一个节点链接指向哪些节点。
所以在邻接表中,我们要获取 节点cur 链接指向哪些节点,就是遍历 graph[cur节点编号] 这个链表。
接下来就是更新 非访问节点到源点的距离,代码实现和 朴素dijkstra 是一样的,代码如下:
for edge in edges[cur_node]:
if not visited[edge.to] and cur_dict + edge.val < minDist[edge.to]:
minDist[edge.to] = cur_dict + edge.val
heapq.heappush(pq,(minDist[edge.to],edge.to))方法一: 最小堆优化
import heapq
import sys
class Edge:
def __init__(self,to,val) -> None:
self.to = to
self.val = val
def dijkstra(edges,n,start,end):
visited = [False] * (n+1)
minDist = [float('inf')] * (n+1)
minDist[start] = 0
pq = []
heapq.heappush(pq,(0,start))
while pq:
cur_dict,cur_node = heapq.heappop(pq)
if visited[cur_node]:
continue
visited[cur_node] = True
for edge in edges[cur_node]:
if not visited[edge.to] and cur_dict + edge.val < minDist[edge.to]:
minDist[edge.to] = cur_dict + edge.val
heapq.heappush(pq,(minDist[edge.to],edge.to))
return -1 if minDist[end] == float('inf') else minDist[end]
if __name__=="__main__":
input = sys.stdin.read
data = input().split()
# n个车站,m条公路
n = int(data[0])
m = int(data[1])
edges = [[] for i in range(n+1)]
index = 2
for i in range(m):
start = int(data[index])
to = int(data[index+1])
val = int(data[index+2])
edges[start].append(Edge(to,val))
index += 3
res = dijkstra(edges,n,start=1,end=n)
print(res)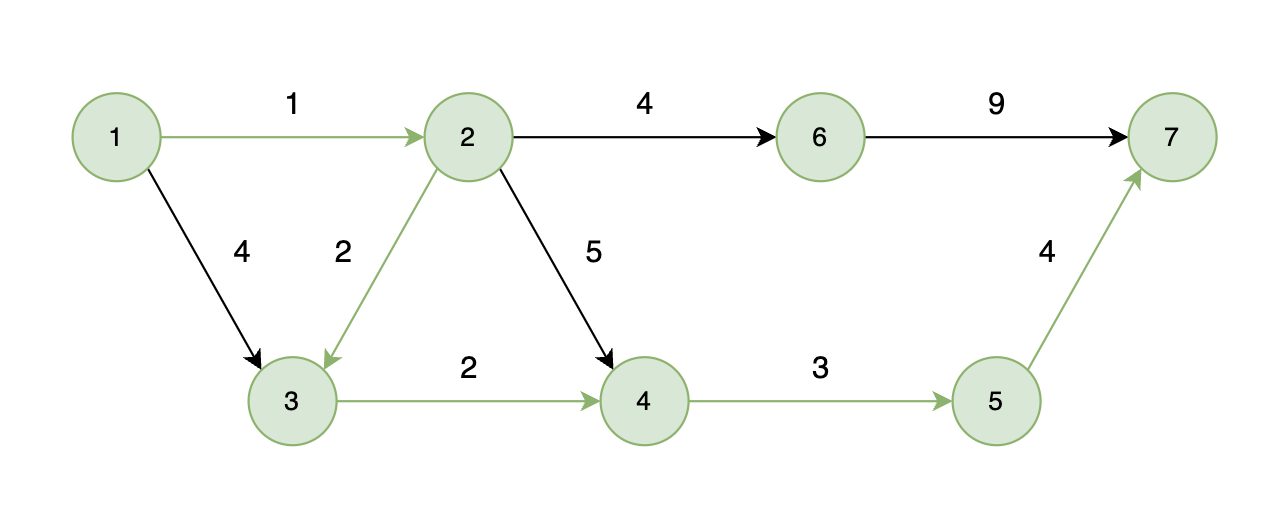
















![[Golang] Channel](https://img-blog.csdnimg.cn/img_convert/9a50f6e400871416a27c4c6b16d51301.png)

