声明
本文章中所有内容仅供学习交流，抓包内容、敏感网址、数据接口均已做脱敏处理，严禁用于商业用途和非法用途，否则由此产生的一切后果均与作者无关，若有侵权，请联系我立即删除！
学习目标
ipv6代理池学习
前置环境配置
-
要求linux系统。我是pve下的ubuntu -
golang的环境 我的是1.18.2
输入 ip a查看网络配置，找到ipv6代理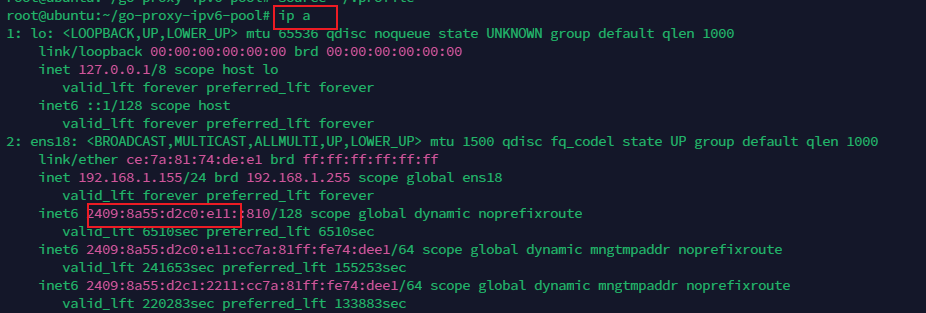 
取这里的前四位+/64 example-->2109:3f21:d2c0:e11::810/64
通过默认互联网接口添加路由
ip route add local 2109:3f21:d2c0:e11::810/64 dev ens18
打开ip_nonlocal_bind绑定任意IP地址：
sysctl net.ipv6.ip_nonlocal_bind=1
对于 IPv6 NDP，安装ndppd ：
apt install ndppd
nano /etc/ndppd.conf
//输入下面
route-ttl 30000
proxy <INTERFACE-NAME>(输入你网卡名字) { router no timeout 500 ttl 30000 rule <IP6_SUBNET> (输入你ipv6的前缀){ static } } //下面是我的配置 route-ttl 30000 proxy ens18 { router no timeout 500 ttl 30000 rule 2109:3f21:d2c0:e11::810/64{ static } } 重新启动ndppd服务：
service ndppd restart
那么接下来我们部署我们的server端
git clone https://github.com/XiaoMiku01/go-proxy-ipv6-pool
cd go-proxy-ipv6-pool
Random ipv6 egress proxy server (support http/socks5) 随机ipv6出口代理服务器（支持http/socks5）
go run . --port <port> --cidr < your ipv6 cidr > # e.g. 2001:399:8205:ae00::/64
//我们的命令
go run . --port 1552 --cidr 2109:3f21:d2c0:e11::810/64
部署完server端接下来我们去curl去解析一下
curl -x http://127.0.0.1:1552 ipv6.ip.mir6.com
curl -x http://127.0.0.1:1552 http://6.ipw.cn/
curl -x socks5://127.0.0.1:1553 http://6.ipw.cn/
while true; do curl -x http://127.0.0.1:1552 ipv6.ip.sb; done
调用server端的代理
import requests
# 设置代理
proxy = {
'http': 'http://192.168.1.155:1552',
'https': 'http://192.168.1.155:1552'
} # 目标URL url = 'http://ipv6.ip.mir6.com' # 发送请求 response = requests.get(url, proxies=proxy) # 打印响应内容 print(response.text) 最终成功图
可以看到啊。我们去请求的话，是从我们的ipv6生成返回过来的随机ipv6地址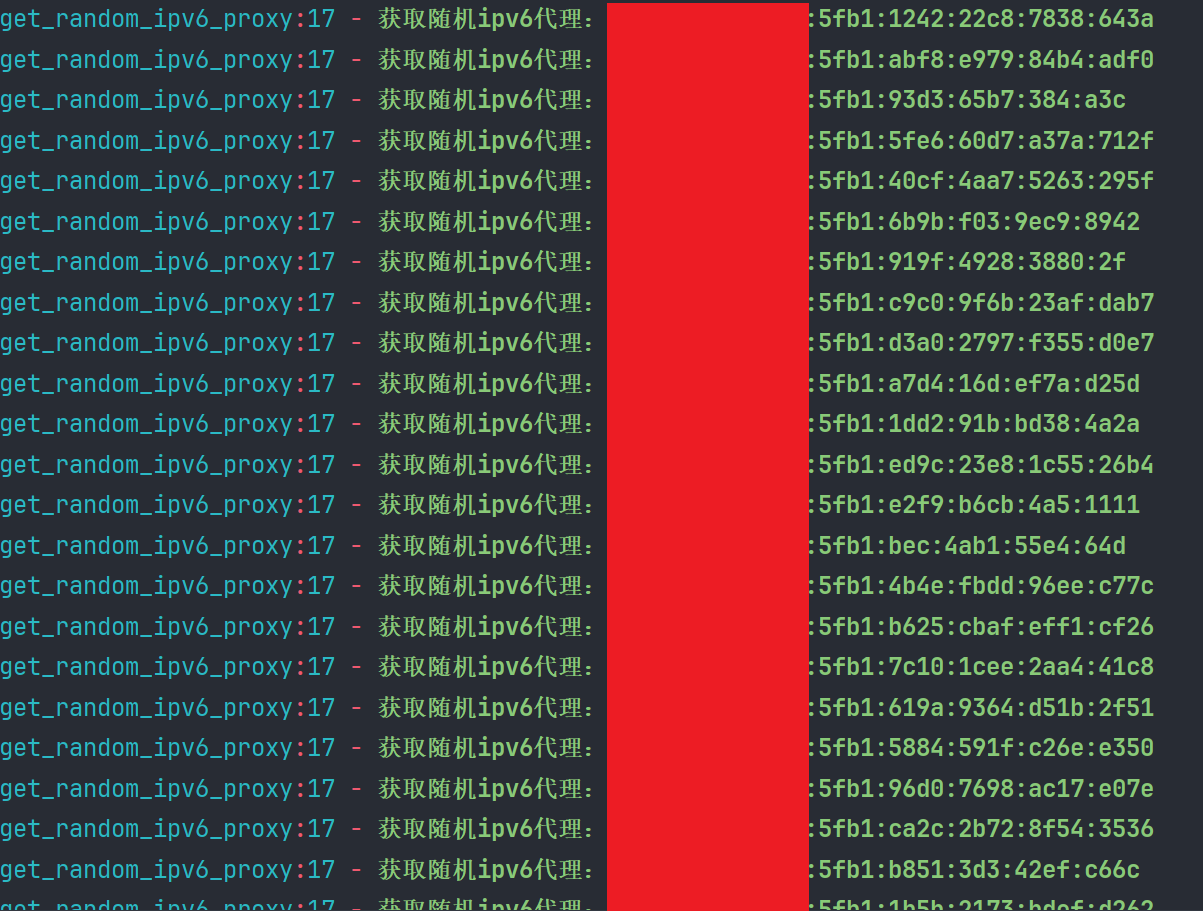 
经过部分站测试，支持ipv6且不封段，可达到并发爬取效果
感谢GitHub开源项目以及链接、文章
相关文章
-
浅谈 IPv6 的入侵与防御 -
“失控”的 IPv6：观察 IPv6 网络环境安全现状 -
谁不想要 2^64 个 IP 的代理池 ？ -
利用IPV6绕过B站的反爬 -
谁不想要 2^64 个 IP 的代理池 ？git项目 -
Go Proxy IPV6 Pool -
基于ip6tables构建随机出口
Next-Target
-
阿里140 -
主动调用Android-Wechat文本信息 -
腾讯滑块tdc -
顶象 -
数美 -
js盾
最近想法
我开了个知识星球，把将本期搭建写成shell脚本已放到了里面，有需要的小伙伴可以自行去取，jd的参数，阿里bxet纯算、快手滑块，Pdd—Anti，ikuai，b站login之-极验3文字，某音ab，瑞数456vmp补环境等等，主要是某些大佬加我问成品，很多人都打着白嫖的手段去加我好友为目的，问完基本就以后没有任何的交集，这样的交好友雀氏没有任何意义。不如我直接开个星球，里面直接放我逆向的成品以及逆向的思路，这样大家各取所需，我也有点收益，意义更明确点，免得浪费大家的时间。星球如果你们遇到了什么问题的话，也可以直接提出来，我肯定以我最大的能力去回答，后续的话，随着知识星球的作品和思路越来越多，涨价是必然的。至于一些没有特殊难点的站或app，我会直接把思路以及成品到星球里面，同时也欢迎各位大佬的技术合作，有技术，有想法的一起交流成长。
本文使用 mdnice 排版
