引言

对于任意两个拓扑结构相似的表面，可以计算它们之间的一一对应映射。如果其中一个表面由三角形网格表示，那么计算这种映射的问题被称为网格参数化。映射到的表面通常被称为参数域。表面网格与各种域之间的参数化在计算机图形学和几何处理中有广泛的应用，如下所述。近年来，针对参数化网格的方法层出不穷，目标是不同的参数域，并侧重于不同的参数化属性。

本课程将回顾各种参数化方法，总结每种技术的主要思想，并侧重于方法的实践方面。它还提供了许多更受欢迎的方法生成的结果示例。当几种方法解决相同的参数化问题时，本综述努力基于参数化质量、效率和鲁棒性等标准提供客观比较。我们还将详细讨论从参数化中受益的应用，并讨论实施不同技术时涉及的实际问题。

1.1 应用

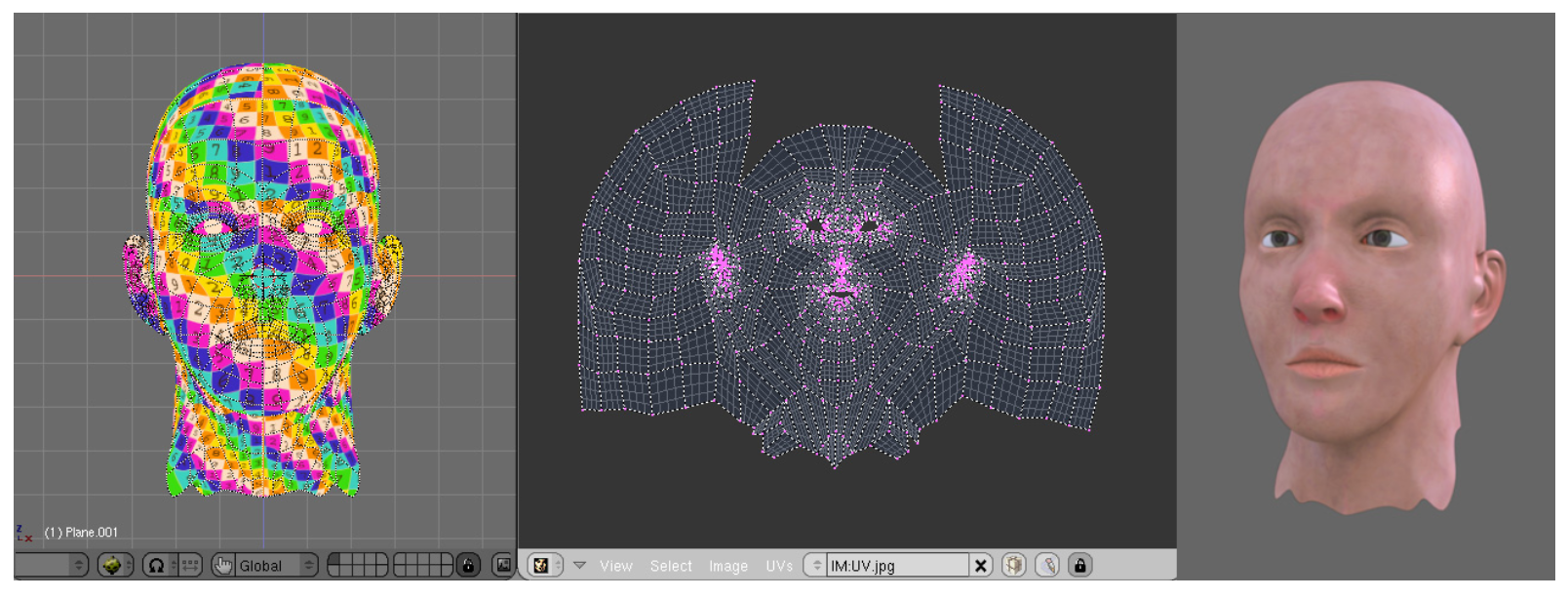
表面参数化最初作为将纹理映射到表面的方法引入计算机图形学[Bennis等人，1991年; Maillot等人，1993年]。在过去的十年中，它逐渐成为一种无处不在的工具，适用于许多网格处理应用，如下所述。

细节映射

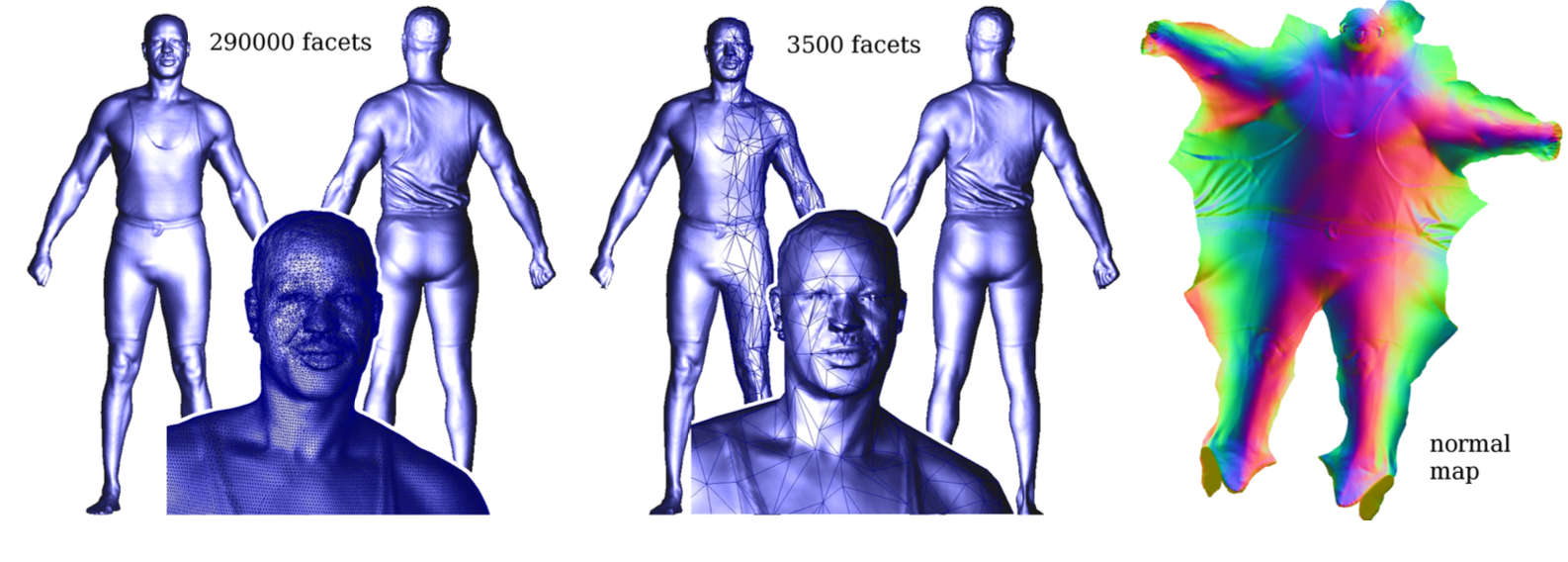
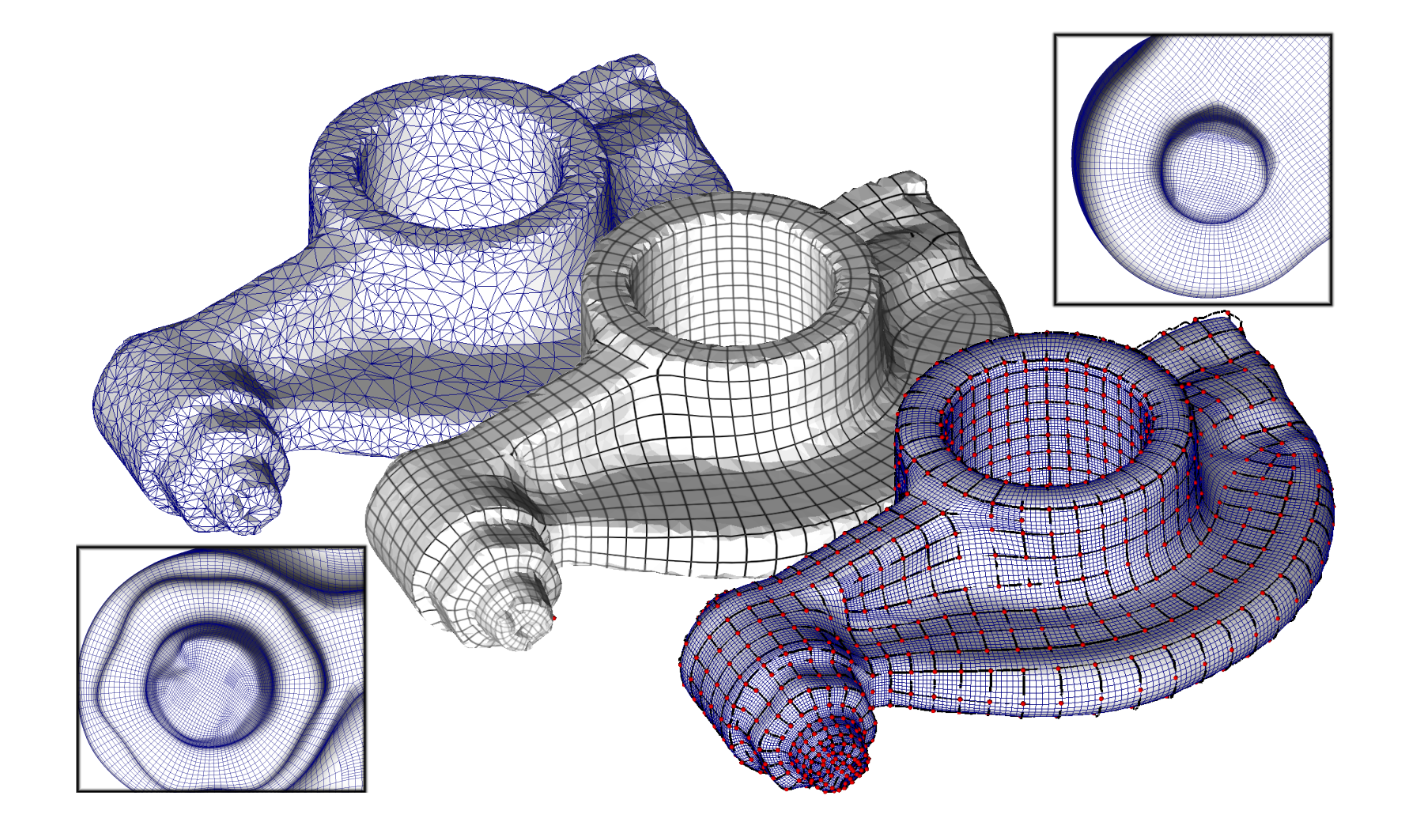
复杂的对象可以通过一个粗糙的几何形状（多边形网格或细分表面）高效表示，每个三角形对应细节存储在单独的二维数组中。在传统的纹理映射中，细节是相应像素的颜色。通过存储凹凸、法线或位移图，模型可以进一步丰富。最近的技术[Peng等人，2004年; Porumbescu等人，2005年]使用体积纹理而不是二维纹理来模拟表面附近的厚区域空间，以建模具有复杂拓扑或不易通过高度场局部近似的细节，例如稀疏交织的结构或动物皮毛。将细节映射到表面的自然方式是使用平面参数化。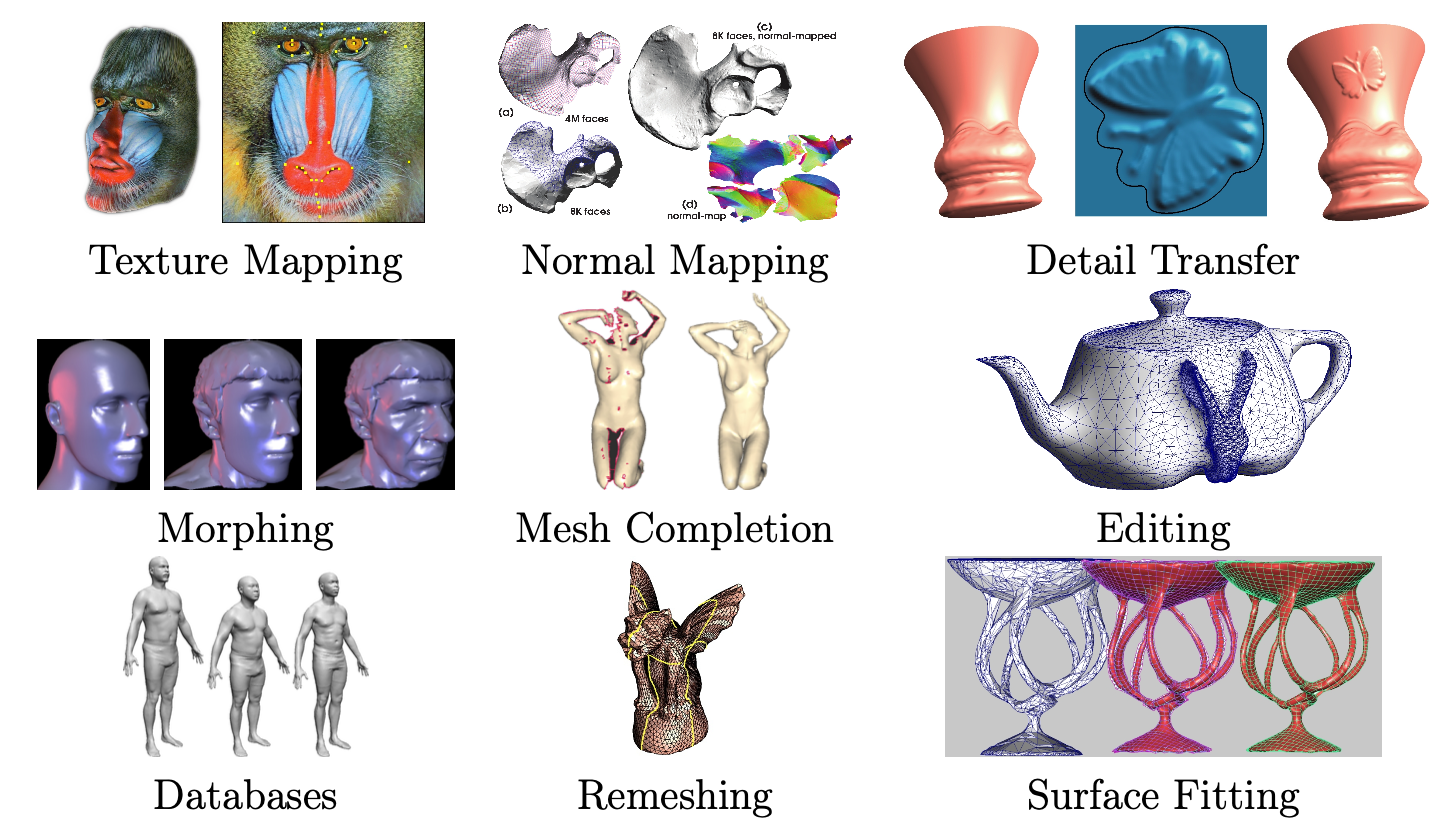

细节合成

虽然纹理映射的目标是表现3D物体的复杂外观，但有几种方法利用网格参数化来创建丰富外观所需的局部细节。这些技术可以使用平面补丁作为输入，其中包含样本细节，例如 [Soler et al., 2002]；参数化或程序化模型；或直接的用户输入和编辑 [Carr and Hart, 2004]。细节的类型可以非常多样，用于创建它的中间表示与用于存储它的最终表示相似。

变形和细节转移

两个物体表面之间的映射允许将细节从一个物体转移到另一个物体（例如 [Praun et al., 2001]），或在几个物体的形状和外观之间进行插值 [Alexa, 2000; Kraevoy and Sheffer, 2004; Schreiner et al., 2004]。通过随时间改变插值比率，可以产生变形动画。在空间变化和频率变化的变形中，物体不同部分或不同频带（被转换特征的粗细程度）的变化率可以不同 [Allen et al., 2003; Kraevoy and Sheffer, 2004]。这种映射可以直接计算，或者更常见的是通过将两个物体表面映射到一个共同的域来计算。除了转移表面的静态外观，表面间参数化还允许在形状之间转移动画数据，可以通过转移来自动画骨骼的局部表面影响，或直接转移网格中每个三角形的局部仿射变换 [Sumner and Popović, 2004]。

网格补全

来自范围扫描的网格通常包含孔洞和多个组件。Lévy [2003] 使用平面参数化来获得孔洞边界的自然形状并对其进行三角剖分。在许多情况下，关于扫描模型整体形状的先验知识是存在的。例如，对于人体扫描，通用人体形状的模板很容易获得。Allen et al. [2003] 和 Anguelov et al. [2005] 利用这种先验知识来促进扫描的补全，方法是计算扫描与模板人体模型之间的映射。Kraevoy 和 Sheffer [2005] 开发了一种更通用和稳健的基于模板的方法，用于补全任何类型的扫描。这些技术通常使用模板和扫描之间的表面间参数化。

网格编辑

编辑操作通常受益于模型对之间的局部参数化。Biermann等人[2002]使用局部参数化来促进模型之间的细节剪切和粘贴转移。他们在2D中局部参数化两个模型上的感兴趣区域，并重叠这两个参数化。他们使用参数化将形状属性从一个模型转移到另一个模型。Lévy [2003]以类似的方式使用局部参数化进行网格组合。他们计算输入模型上靠近组合边界区域的重叠平面参数化，并用它来提取和平滑混合两个模型的形状信息。

创建对象数据库

一旦大量模型在共同域上参数化，就可以进行分析，确定对象之间的共同因素和它们的区别特征。例如，在人体形状数据库中[Allen等人，2003]，区别特征可能是性别、身高和体重。可以将对象与数据库进行比较，并在这些维度上进行评分，数据库可以通过插值或外推现有对象来创建新的合理对象实例。

重新网格化

有许多可能的三角剖分可以用相似的精度水平表示相同的形状。对于不同的应用，某些三角剖分可能比其他的更理想。例如，对于表面上的数值模拟，具有良好纵横比的三角形（不太小或不太细）对于收敛性和数值精度很重要。重新网格化表面或用另一种三角剖分替换一种三角剖分的一种常见方法是参数化表面，然后将域的理想的、易于理解和创建的三角剖分映射回原始表面。例如，Gu等人[2002]使用平面正方形域的规则网格采样，而其他方法，如[Guskov等人，2000]在简单域的面上使用规则细分（通常是1比4三角形分割）。这种局部规则网格通常可以支持通过应用细分规则的极限过程创建光滑表面。为了生成高质量的三角剖分，Desbrun等人[2002]将输入网格参数化到平面中，然后使用平面Delaunay三角剖分来获得表面的高质量重新网格化。这些方法面临的一个问题是沿着为促进参数化而创建的切割线出现可见的不连续性。Surazhsky和Gotsman [2003]避免全局参数化，而是使用局部参数化作为显式重新网格化方案的一部分，在网格上移动顶点。最近的方法，如[Ray等人，2006]使用全局参数化直接在3D表面上生成以四边形为主的网格。

网格压缩

网格压缩用于紧凑地存储或传输几何模型。与其他数据一样，压缩率与数据熵成反比。因此，当模型由尽可能规则的网格表示时，无论在拓扑上还是几何上，都可以获得更高的压缩率。拓扑规则性指的是几乎所有顶点都具有相同度数的网格。几何规则性意味着三角形在形状和大小上彼此相似，且顶点接近其邻居的质心。这样的网格可以通过参数化原始对象，然后用规则采样模式重新网格化来获得[Gu等人，2002]。参数化的质量直接影响压缩效率。

表面拟合

网格参数化的早期应用之一是表面拟合[Floater，2000]。几何处理中的许多应用需要从输入网格构建平滑的分析表面。网格在基础域上的参数化显著简化了这项任务。早期方法要么将整个网格参数化到平面，要么将其分段并独立参数化每个片段。最近的方法，例如[Li等人，2006]，专注于构建平滑的全局参数化并用于拟合，实现了构建表面的全局连续性。

从材料片建模

虽然计算机图形学专注于虚拟模型，但几何处理有许多现实世界的工程应用。特别是，平面网格参数化是从材料片建模3D对象时的重要工具，范围从服装建模到金属成型或锻造[Bennis等人，1991; Julius等人，2005]。所有这些应用都需要计算平面图案以形成所需的3D形状。通常，模型首先被分割成几乎可展开的图表，然后这些图表在平面中参数化。

医学可视化

复杂的几何结构通常通过将表面法线图、颜色和其他属性映射到更简单的规范域来更好地可视化和分析。人脑是这种映射特别有用的结构之一[Hurdal等人，1999; Haker等人，2000]。大多数脑映射方法利用大脑是零亏格的事实，通过球面[Haker等人，2000]或平面[Hurdal等人，1999]参数化来可视化它。

第2章 微分几何入门

在我们详细讨论如何计算网格参数化及其应用之前，让我们快速回顾一些来自微分几何的基本性质，这些性质对于理解后面所描述的方法的动机至关重要。有关这些性质的详细信息和证明，我们建议读者参考微分几何的标准文献，特别是do Carmo [1976]、Klingenberg [1978]、Kreyszig [1991]和Morgan [1998]的书籍。

2.1 基本定义

假设Ω ⊂ R²是一个简单连通区域（即没有任何孔），例如：

• 单位正方形：Ω = {(u,v) ∈ R² : u,v ∈ [0,1]}，
• 或单位圆盘：Ω = {(u,v) ∈ R² : u²+v² ≤ 1}。

假设函数f : Ω → R³是连续且单射的（即Ω中的任何两个不同点在R³中对应的点都不同）。我们称Ω在f下的像S为一个曲面：
[ S = f(Ω) = {f(u,v) : (u,v) ∈ Ω} ]，

并称f是S在参数域Ω上的参数化。根据S的定义，f实际上是Ω和S之间的双射，因此可以定义它的逆函数f⁻¹ : S → Ω。以下是一些例子：

1. 简单线性函数：
   • 参数域：Ω = {(u,v) ∈ R² : u,v ∈ [0,1]}
   • 曲面：S = {(x,y,z) ∈ R³ : x,y,z ∈ [0,1], x+y = 1}
   • 参数化：f(u,v) = (u, 1−u, v)
   • 逆函数：f⁻¹(x, y, z) = (x, z)

2. 圆柱：

• 参数域：Ω = {(u,v) ∈ R² : u ∈ [0,2π), v ∈ [0,1]}
• 曲面：S = {(x,y,z) ∈ R³ : x² + y² = 1, z ∈ [0,1]}
• 参数化：f(u, v) = (cos u, sin u, v)
• 逆函数：f⁻¹(x, y, z) = (arccos x, z)

3. 抛物面：

• 参数域：Ω = {(u, v) ∈ R² : u, v ∈ [−1, 1]}
• 曲面：S = {(x, y, z) ∈ R³ : x, y ∈ [−2, 2], z = 4(x² + y²)}
• 参数化：f(u, v) = (2u, 2v, u² + v²)
• 逆函数：f⁻¹(x, y, z) = (x/2, y/2)

4. 半球面（正投影）：

• 参数域：Ω = {(u, v) ∈ R² : u² + v² ≤ 1}
• 曲面：S = {(x, y, z) ∈ R³ : x² + y² + z² = 1, z ≥ 0}
• 参数化：f(u, v) = (u, v, √(1 − u² − v²))
• 逆函数：f⁻¹(x, y, z) = (x, y)

定义了一个曲面S之后，我们应该注意到，函数f绝不是S在Ω上的唯一参数化。事实上，给定任何双射φ : Ω → Ω，很容易验证f和φ的复合函数，即g = f ◦ φ，也是S在Ω上的一个参数化。例如，我们可以通过定义从任何双射ρ : [0, 1] → [0, 1]轻松构造这样的重新参数化φ：

• 对于单位正方形：φ(u, v) = (ρ(u), ρ(v))
• 对于单位圆盘：φ(u, v) = (uρ(u² + v²), vρ(u² + v²))

特别地，取函数ρ(x) = 2/（1 + x），并将这种重新参数化应用于上例中半球面的参数化，得到以下替代参数化：

5. 半球面（立体投影）：

参数域：Ω = {(u, v) ∈ R² : u² + v² ≤ 1}

曲面：S = {(x, y, z) ∈ R³ : x² + y² + z² = 1, z ≥ 0}

参数化：$ f(u, v) = (\left(\frac{2u}{1 + u2 + v2}, \frac{2v}{1 + u2 + v2}, \frac{1 - u2 - v2}{1 + u2 + v2}\right)) $

逆函数：$ f⁻¹(x, y, z) = (\left(\frac{x}{1 + z}, \frac{y}{1 + z}\right)) $

这种参数化方法被称为立体投影，它具有以下特点：

1. 保角性：立体投影保持了角度，这在某些应用中非常重要。
2. 共形映射：它是一种共形映射，意味着它在局部保持形状。
3. 无奇点：除了北极点（在这个半球面的情况下是(0,0,1)）外，映射是平滑的。
4. 双有理函数：参数化和其逆都是有理函数，这在某些计算中可能有优势。

立体投影在地图制图、复分析和其他数学领域中有重要应用。它提供了一种将球面（或半球面）上的点与平面上的点进行对应的方法，这在处理球面几何问题时非常有用。

2.2 内在曲面性质

虽然曲面的参数化不是唯一的——我们将在后面讨论如何根据某些标准获得“最佳”参数化——但它仍然是一个非常方便的工具，因为它可以用来计算曲面的各种性质。例如，如果f是可微的，那么它的偏导数

$ f_u = \frac{\partial f}{\partial u} 和 f_v = \frac{\partial f}{\partial v} $

展开了局部切平面，通过简单地计算它们的叉积并归一化结果，我们得到曲面的法向量

$ n_f = \frac{f_u \times f_v}{||f_u \times f_v||} $

为了简化符号，我们常将$ ( f_u )和( f_v ) $<fontstyle="color:rgba(0,0,0,0.82);">称为导数，将</font>$ ( n_f ) $<fontstyle="color:rgba(0,0,0,0.82);">称为曲面法向量，但我们应当记住，形式上这三者都是从R^2到R^3的函数。换句话说，对于参数域\Omega 中的任意点(u,v)，在曲面点(f(u,v))\in S处的切平面由向量</font>$ f_u(u,v) 和f_v(u,v)张成，而n_f(u,v) $是此点的法向量。

我们通过考虑两个例子来澄清这一点：

1. 对于简单的线性函数$ f(u,v) = (u,1−u,v) $<fontstyle="color:rgba(0,0,0,0.82);">，我们得到</font>$ f_u(u,v) = (1,−1,0) $$ 和 f_v(u,v) = (0,0,1) $<fontstyle="color:rgba(0,0,0,0.82);">进一步计算得到</font>$ n_f(u,v) = \left(\frac{-1}{\sqrt{2}}, \frac{1}{\sqrt{2}}, 0\right) $,这表明所有S上的点的法向量是一个常量。
2. 对于圆柱的参数化，$ f(u,v) = (\cos u, \sin u, v) $<fontstyle="color:rgba(0,0,0,0.82);">，我们得到</font>$ f_u(u,v) = (−\sin u, \cos u, 0) 和 f_v(u,v) = (0,0,1) $<fontstyle="color:rgba(0,0,0,0.82);">进一步计算得到</font>$ n_f(u,v) = (\cos u, \sin u, 0) $,这表明S上任意点(x, y, z)的法向量只是(x, y, 0)。

注意，在两个例子中，曲面法向量都与参数化无关。事实上，这对所有曲面都成立，因此称为曲面的内在性质。正式地，我们还可以说曲面法向量是一个函数( n : S → S² )，其中( S² = {(x,y,z) ∈ R³ : x² + y² + z² = 1} )是R³中的单位球面，因此

$ n§ = n_f(f^{-1}§) $

对于任何 p ∈ S 和任何参数化 f 。作为练习，你可以验证这一点对于上面给出的半球面的两种替代参数化是否成立。其他内在曲面性质包括高斯曲率 K§ 和平均曲率 H§ ，以及曲面的总面积 A(S) 。为了计算后者，我们需要使用第一基本形式。

$ I_f = \begin{pmatrix}
f_u \cdot f_u & f_u \cdot f_v \
f_v \cdot f_u & f_v \cdot f_v
\end{pmatrix} = \begin{pmatrix}
E & F \
F & G
\end{pmatrix}, $

其中偏导数之间的乘积是$ \mathbb{R}^3 $中的常规点积。根据柯西-施瓦茨不等式，这个对称的$ 2 \times 2 $矩阵的行列式总是非负的，因此它的平方根总是实数。曲面的面积定义为

$ A(S) = \int_{\Omega} \sqrt{\det I_f} , du , dv. $

例如，考虑半球在单位圆盘上的正交参数化$ f(u, v) = (u, v, \sqrt{1 - u^2 - v^2}) $。经过一些简化，我们发现

$ \det I_f = \frac{1}{1 - u^2 - v^2} $

可以计算半球的面积如下：

$ A(S) = \int_{-1}^{1} \int_{-\sqrt{1-v^2}}{\sqrt{1-v^2}} \frac{1}{\sqrt{1 - u^2 - v^2}} , du , dv\
= \int_{-1}^{1} \left[ \arcsin \frac{u}{\sqrt{1 - v^2}} \right]{-\sqrt{1-v^2}}{\sqrt{1-v^2}} , dv \
= \int{-1}^{1} \pi , dv \
= 2\pi, $

正如预期的那样。当然，如果我们使用立体投影参数化，也会得到相同的结果，你可以尝试将其作为练习。

为了计算曲率，我们必须首先假设参数化是二阶可微的，以便其二阶偏导数

$ f_{uu} = \frac{\partial^2 f}{\partial u^2}, \quad f_{uv} = \frac{\partial^2 f}{\partial u \partial v}, \quad f_{vv} = \frac{\partial^2 f}{\partial v^2} $

是良好定义的。将这些导数与曲面法向量进行点积，然后得到称为第二基本形式的对称2×2矩阵：

$ II_f = \begin{pmatrix}
f_{uu} \cdot n_f & f_{uv} \cdot n_f \
f_{uv} \cdot n_f & f_{vv} \cdot n_f
\end{pmatrix} = \begin{pmatrix}
L & M \
M & N
\end{pmatrix} $

其中：

• ( f_{uu} )、( f_{uv} )、( f_{vv} ) 是参数化函数的二阶偏导数。
• ( n_f ) 是曲面的法向量。
• ( L )、( M )、( N ) 是矩阵的元素，表示二阶基本形式的系数。

这个矩阵用于描述曲面的局部弯曲性质，是微分几何中的一个重要工具。

如何计算曲面的曲率，并引入了第二基本形式的概念：

1. 立体投影参数化：文中提到使用立体投影参数化计算曲面面积会得到相同的结果。
2. 曲率计算的前提：为了计算曲率，参数化必须是二阶可微的，这样才能定义二阶偏导数。
3. 二阶偏导数：包括 ( f_{uu} )、( f_{uv} ) 和 ( f_{vv} )，分别表示参数化函数关于 ( u ) 和 ( v ) 的二阶偏导数。
4. 第二基本形式：通过将二阶偏导数与曲面法向量的点积，得到一个对称的2×2矩阵，称为第二基本形式。矩阵元素通常用 ( L )、( M )、( N ) 表示。

第二基本形式在微分几何中用于描述曲面的曲率性质。它与第一基本形式一起，提供了关于曲面几何形状的完整信息。这些概念在计算机图形学、物理学和工程学中有广泛应用，特别是在曲面建模和分析中。

高斯曲率和平均曲率分别定义为矩阵 $ I^{-1}II_f $的行列式和迹的一半；高斯曲率 ( K ) 和平均曲率 ( H ) 的表达式为：

$ K = \det(I^{-1}I!I_f) = \frac{\det I!I_f}{\det I_f} = \frac{LN - M^2}{EG - F^2} $

$ H = \frac{1}{2} \text{trace}(I^{-1}I!I_f) = \frac{1}{2} \frac{LG - 2MF + NE}{EG - F^2} $

例如，通过进行这些计算可以发现，对于上述大多数曲面，其曲率是常数：

• 简单线性函数：( K = 0 )、( H = 0 )
• 圆柱面：( K = 0 )、( $ H = \frac{1}{2} $ )
• 半球面：( K = 1 )、( H = -1 )

作为练习，证明抛物面在任一点 ( p = (x, y, z) ) 的曲率为：

$ K§ = \frac{1}{4(1+z)^2} $

$ H§ = \frac{2+z}{4(1+z)^{3/2}} $

通过第一基本形式和第二基本形式的矩阵运算来定义曲面的高斯曲率和平均曲率，并给出了具体的例子说明不同曲面上的曲率值。最后，提出了一个练习，要求读者证明抛物面上任一点的曲率公式。

2.3 度量失真

除了这些内在的曲面性质之外，还有其他性质依赖于参数化，最重要的是度量失真。例如，考虑上面半球的两种参数化。在这两种情况下，右侧的曲面图像上都叠加了一个规则的网格，这实际上是左侧参数域中的相应网格的图像。你会注意到，对于立体投影来说，曲面网格看起来比正射投影更规则，而后者在边界附近沿径向明显地拉伸网格。

为了更好地理解这种拉伸，我们来看看当我们在参数域中稍微偏离点 (u, v) 时，曲面点 f(u, v) 会发生什么。如果我们用 (Δu, Δv) 表示这个无穷小的参数位移，那么新的曲面点 f(u+Δu, v+Δv) 可由 f 在 (u, v) 处的一阶泰勒展开近似表示：

$ \tilde{f}(u + \Delta u, v + \Delta v) = f(u, v) + f_u(u, v)\Delta u + f_v(u, v)\Delta v. $

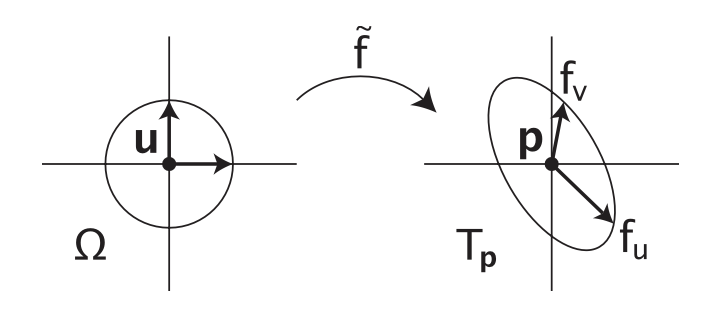
这个线性函数将 u = (u, v) 附近的所有点映射到切平面 T_p 上，其中 p = f(u, v) ∈ S，并将围绕 u 的圆变换为围绕 p 的椭圆（见图 2.1）。如果我们更紧凑地写出泰勒展开式，这一性质变得显而易见：

$ \tilde{f}(u+\Delta u, v+\Delta v) = p + J_f(u) \begin{pmatrix} \Delta u \ \Delta v \end{pmatrix}, $

其中 J_f = (f_u f_v) 是 f 的雅可比矩阵，即一个以 f 的偏导数为列向量的 3 × 2 矩阵。然后利用雅可比矩阵的奇异值分解：

$ J_f = U\Sigma V^T = U \begin{pmatrix} \sigma_1 & 0 \ 0 & \sigma_2\ 0 & 0 \end{pmatrix} V^T, $

这里介绍了如何通过分析参数化曲面的雅可比矩阵来理解度量失真。这个过程展示了当在参数域中进行微小位移时，曲面点如何被映射到其相应的切平面上，以及这种映射如何扭曲空间结构，例如将圆转换为椭圆。奇异值分解在理解这种变化的尺度和方向上起着关键作用。

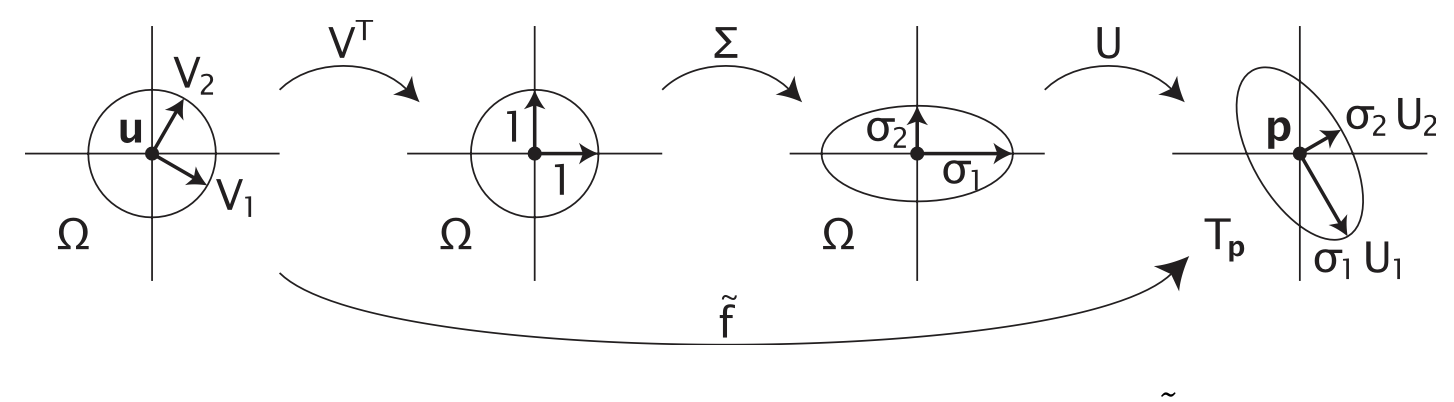
对于奇异值 σ1 ≥ σ2 > 0 和正交矩阵 U ∈ R3×3 和 V ∈ R2×2（其列向量分别为 U1, U2, U3 和 V1, V2），我们可以将线性变换 f̃ 分解为如图2.2所示的步骤：

1. 变换 V^T 首先围绕 u 旋转所有点，使得向量 V1 和 V2 分别与 u 轴和 v 轴对齐。
2. 变换 Σ 然后在 u 方向上以因子 σ1 拉伸，在 v 方向上以因子 σ2 拉伸。
3. 最后，变换 U 将单位向量 (1, 0) 和 (0, 1) 映射到切平面 T_p 上的向量 U1 和 U2。

这种将圆变为椭圆的变换被称为参数化的局部度量畸变，它展示了 f 在参数域中某点 u ∈ Ω 附近以及相应的曲面点 p = f(u) ∈ S 附近的局部行为。此外，关于这种局部度量畸变的所有信息都包含在奇异值 σ1 和 σ2 中。例如：

• 如果两个奇异值相等，那么 J_f 就只是一个旋转加均匀缩放，f 在 u 附近不会扭曲角度。
• 如果奇异值的乘积为1，那么参数域中任何圆的面积与切平面中相应椭圆的面积相同，我们称 f 为局部保面积的。

直接计算奇异值比较复杂，因此我们可以利用一个事实：任何矩阵 A 的奇异值是矩阵 A^T A 的特征值的平方根。在我们的例子中，矩阵 $ J_f^T J_f $就是我们熟悉的第一基本形式。

$ J_f^T J_f = I_f = \begin{pmatrix}
f_u^T f_u & f_u^T f_v \
f_v^T f_u & f_v^T f_v
\end{pmatrix} = \begin{pmatrix}
E & F \
F & G
\end{pmatrix} $

因此，任何以 u 为中心、半径为 r 的圆将被映射为以 p 为中心、半轴长度为 rσ1 和 rσ2 的椭圆，正交标架 [V1, V2] 被映射为正交标架 [σ1U1, σ2U2]。

我们可以使用一个巧妙的小公式轻松计算这个对称矩阵的两个特征值 λ1 和 λ2：

λ1,2 = 1/2 (E + G) ± √(4F² + (E - G)²)

现在，我们总结一下参数化在局部可能具有的主要性质：

1. f 是等距的或保长的 ⇐⇒ σ1 = σ2 = 1 ⇐⇒ λ1 = λ2 = 1
2. f 是共形的或保角的 ⇐⇒ σ1 = σ2 ⇐⇒ λ1 = λ2
3. f 是等面积的或保面积的 ⇐⇒ σ1σ2 = 1 ⇐⇒ λ1λ2 = 1

显然，任何等距映射都是共形的和等面积的，而每个既是共形又是等面积的映射也是等距的。简而言之：

等距 ⇐⇒ 共形 + 等面积

有了这些知识，让我们回到之前的例子，检查它们的性质：

1. 简单线性函数：

                     参数化：$ f(u, v) = (u, 1 - u, v) $
   
                      雅可比矩阵：$ J_f = \begin{pmatrix} 1 & 0 \\ -1 & 0 \\ 0 & 1 \end{pmatrix} $
   
                      第一基本形式：$ I_f = \begin{pmatrix} 2 & 0 \\ 0 & 1 \end{pmatrix} $
   
                      特征值：$ \lambda_1 = 2, \quad \lambda_2 = 1 $
   

   这个参数化既不是共形的，也不是等面积的。

2. 圆柱：

        参数化：$ f(u, v) = (\cos u, \sin u, v) $
   
        雅可比矩阵：$ J_f = \begin{pmatrix} -\sin u & 0 \\ \cos u & 0 \\ 0 & 1 \end{pmatrix} $
   
        第一基本形式：$ I_f = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} $
   
        特征值：$ \lambda_1 = 1, \quad \lambda_2 = 1 $
   
   这个参数化是等距的。
   

3. 抛物面：

           参数化：$ f(u,v) = (2u, 2v, u^2 + v^2) $
   
          雅可比矩阵：$ J_f = \begin{pmatrix} 2 & 0 \\ 0 & 2 \\ 2u & 2v \end{pmatrix} $
   
          第一基本形式：$ I_f = \begin{pmatrix} 4 + 4u^2 & 4uv \\ 4uv & 4 + 4v^2 \end{pmatrix} $
   
          特征值：$ \lambda_1 = 4, \quad \lambda_2 = 4(1 + u^2 + v^2) $
   

这个映射不是等面积的，仅在 $ (u,v) = (0,0) $处是共形的。

4. 半球（正射投影）：

                        参数化：$ f(u,v) = (u, v, \frac{1}{d}) \quad \text{其中} \quad d = \frac{1}{\sqrt{1 - u^2 - v^2}} $
   
                        雅可比矩阵：$ J_f = \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ -ud & -vd \end{pmatrix} $
   
                        第一基本形式：$ I_f = \begin{pmatrix} 1 + u^2 d^2 & uvd^2 \\ uvd^2 & 1 + v^2 d^2 \end{pmatrix} $
   
                        特征值：$ \lambda_1 = 1, \quad \lambda_2 = d^2 $
   

这个映射在 $ (u,v) = (0,0) $ 处是等距的，但在其他地方既不是共形的也不是等面积的。
5. 半球（立体投影）：

                       参数化：$ f(u,v) = (2ud, 2vd, (1 - u^2 - v^2)d) $$ ，其中  $$ d = \frac{1}{1+u^2+v^2} $

                       雅可比矩阵：$ J_f = \begin{pmatrix} 2d-4u^2d^2 & -4uvd^2 \\ -4uvd^2 & 2d-4v^2d^2 \\ -4ud^2 & -4vd^2 \end{pmatrix} $

                       第一基本形式：$ I_f = \begin{pmatrix} 4d^2 & 0 \\ 0 & 4d^2 \end{pmatrix} $

                       特征值：$ \lambda_1 = 4d^2, \quad \lambda_2 = 4d^2 $

这个映射始终是共形的，但仅在 $ \Omega $$的边界（即$$ u^2 + v^2 = 1 $）处是等面积的，因此也是等距的。

事实证明，唯一在各处都是等距的、因此不引入任何扭曲的最优参数化是圆柱的参数化。实际上，高斯在1827年证明，全局等距参数化仅存在于可展曲面，如平面、圆锥和圆柱，这些曲面在所有表面点$ p \in S $处的高斯曲率 K§ = 0。作为练习，你可以尝试为第一个例子中的平面曲面片找到这样的全局等距参数化。

其他有趣的参数化包括那些全局共形的参数化，如半球的立体投影。黎曼在1851年证明，对于任何拓扑上等价于圆盘的曲面和任何单连通的参数域，这样的参数化是存在的。

更一般地，曲面 S在参数域$ \Omega $上的“最佳”参数化 f 是这样找到的。我们首先需要一个双变量的非负函数 $ E : \mathbb{R}^2 \to \mathbb{R}^{++} $，它用奇异值$ \sigma_1 $和$ \sigma_2 $来衡量参数化的局部扭曲。通常，这个函数在 (1,1) 处有全局最小值，以偏好等距性，但根据应用的不同，它也可以被定义为在整条线 (x,x) 上取得最小值，其中 $ x \in \mathbb{R}^+ $，例如，如果需要优先共形映射。特定参数化 f的整体扭曲通过在整个域上简单地平均局部扭曲来衡量，

$
E(f) = \int_{\Omega} E(\sigma_1(u,v), \sigma_2(u,v)) , du , dv / A(\Omega),
$

然后，通过在所有可接受的参数化空间中最小化 $$E(f)$$ 来找到相对于E的最佳参数化。

小结

本文探讨了曲面的参数化，特别是全局和局部参数化的性质。首先介绍了雅可比矩阵、特征值和等距性在参数化中的作用，并提供了计算特征值的方法。其次，文章着重讨论了等距、共形和等面积的参数化性质及其条件，指出任何等距映射都同时具有共形和等面积的属性。最后，通过对各参数化性质的分析，提供了对曲面映射局部行为的更深理解。

关键点

+ 雅可比矩阵在曲面参数化中起基本作用，有助于衡量参数化的局部扭曲。 + 高斯证明，仅可展曲面如平面、圆锥和圆柱能做到全局等距参数化，高斯曲率为零。 + 黎曼证明，拓扑上等价于圆盘的曲面存在全局共形参数化。 + 特定参数化的整体扭曲可通过平均局部扭曲进行衡量。 + 可通过对称矩阵特征值计算公式获得两个特征值 λ1 和 λ2。 + 等距性、共形性和等面积性是曲面映射的主要局部性质。 + 等距映射同时也是共形和等面积的，三者之间存在数学关系。

参数化的局部性质

特征值计算公式

对于对称矩阵，我们可以使用以下简洁的公式计算两个特征值 λ1 和 λ2：

λ1,2 = 1/2 (E + G) ± √(4F² + (E - G)²)

参数化的主要局部性质

1. **等距（保长）**： - 条件：σ1 = σ2 = 1 - 等价于：λ1 = λ2 = 1 2. **共形（保角）**： - 条件：σ1 = σ2 - 等价于：λ1 = λ2 3. **等面积（保面积）**： - 条件：σ1σ2 = 1 - 等价于：λ1λ2 = 1

性质之间的关系

+ 任何等距映射都是共形的和等面积的 + 任何既是共形又是等面积的映射也是等距的

简而言之：等距 ⇐⇒ 共形 + 等面积

这些性质为我们提供了分析和设计参数化的强大工具，使我们能够更好地理解和控制曲面映射的局部行为。