前言
在日常开发中,我们经常会遇到一些针对复杂数据的处理,这时我们就会针对不同的业务使用不同算法,减少代码的逻辑复杂度,增加项目的可维护性,而为了保障项目的可持续性,一般都会进行算法的封装,当需要使用时,直接调用即可,这里为大家介绍一些常用的基础算法,以供各位大家参考,若有不对或者遗漏之处,欢迎评论区指出。
常用算法集锦
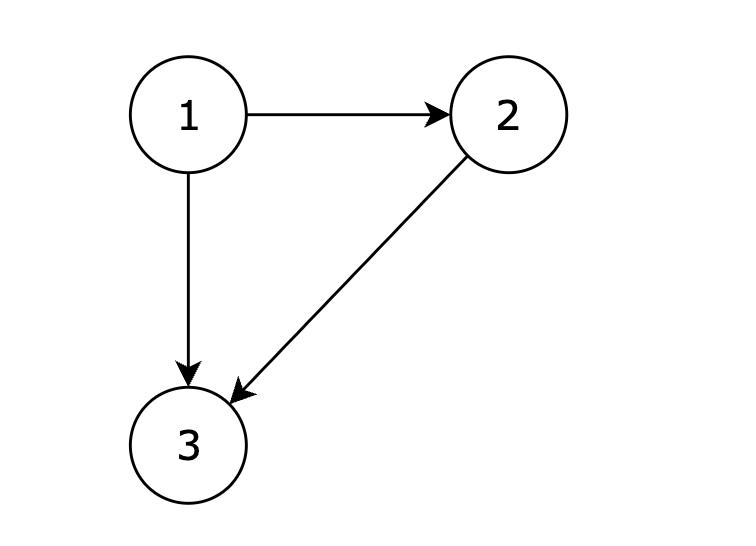
当然,为了更深入地理解深度优先搜索(DFS)和广度优先搜索(BFS),我们可以从基本概念出发,然后通过一个具体的图搜索问题来展示这两种算法的实现。
基本概念
在Go语言中,实现常用算法可以帮助你更好地理解编程逻辑和数据结构。以下是一些常用算法的示例,包括它们的实现过程和代码示例:
-
斐波那契数列:
- 描述:斐波那契数列是一系列数字,其中每个数字是前两个数字的和。
- 实现:可以使用递归或迭代方法实现。
- 代码示例(迭代):
func fibonacci(n int) int { if n <= 1 { return n } a, b := 0, 1 for i := 2; i <= n; i++ { a, b = b, a+b } return b }
-
二分查找:

- 描述:在有序数组中查找某个目标值的位置。
- 实现:通过每次将查找范围缩小一半来查找目标值。
- 代码示例:
func binarySearch(arr []int, target int) int { left, right := 0, len(arr)-1 for left <= right { mid := left + (right-left)/2 if arr[mid] == target { return mid } else if arr[mid] < target { left = mid + 1 } else { right = mid - 1 } } return -1 }
-
冒泡排序:
- 描述:通过重复遍历数组,比较并交换相邻元素来排序。
- 实现:每次遍历都将最大的元素“冒泡”到末尾。
- 代码示例:
func bubbleSort(arr []int) { n := len(arr) for i := 0; i < n-1; i++ { for j := 0; j < n-i-1; j++ { if arr[j] > arr[j+1] { arr[j], arr[j+1] = arr[j+1], arr[j] } } } }
-
递归算法:
- 描述:通过函数自己调用自己来解决问题。
- 实现:定义一个函数,在其内部调用自己。
- 代码示例(计算阶乘):
func factorial(n int) int { if n == 0 { return 1 } return n * factorial(n-1) }
-
快速排序:
- 描述:一种分治法策略的排序算法,通过选择一个“基准”元素,将数组分为两个子数组。
- 实现:递归地对子数组进行快速排序。
- 代码示例:
func quickSort(arr []int) { if len(arr) < 2 { return } left, right := 0, len(arr)-1 for left < right { for left < right && arr[right] >= arr[0] { right-- } arr[left], arr[right] = arr[right], arr[left] for left < right && arr[left] <= arr[0] { left++ } arr[left], arr[right] = arr[right], arr[left] } arr[left], arr[0] = arr[0], arr[left] quickSort(arr[:left]) quickSort(arr[left+1:]) }
-
归并排序:
- 描述:将两个已排序的数组合并成一个更大的已排序数组。
- 实现:递归地将数组分成更小的数组,直到每个数组只有一个元素,然后合并它们。
- 代码示例:
func mergeSort(arr []int) []int { if len(arr) < 2 { return arr } mid := len(arr) / 2 left := mergeSort(arr[:mid]) right := mergeSort(arr[mid:]) var i, j int var result []int for i < len(left) && j < len(right) { if left[i] <= right[j] { result = append(result, left[i]) i++ } else { result = append(result, right[j]) j++ } } return append(append(result, left[i:]...), right[j:]...) }
-
深度优先搜索(DFS):
- 描述:用于遍历或搜索树或图的算法。
- 实现:从一个节点开始,尽可能深地搜索树的分支。
- 代码示例(图的DFS):
func dfs(graph map[int][]int, visited map[int]bool, node int) { visited[node] = true for _, neighbor := range graph[node] { if !visited[neighbor] { dfs(graph, visited, neighbor) } } }
-
广度优先搜索(BFS):
- 描述:从最近的节点开始,逐层遍历图的算法。
- 实现:使用队列来存储每一层的节点。
- 代码示例(图的BFS):
func bfs(graph map[int][]int, start int) { visited := make(map[int]bool) queue := []int{start} visited[start] = true for len(queue) > 0 { current := queue[0] queue = queue[1:] for _, neighbor := range graph[current] { if !visited[neighbor] { visited[neighbor] = true queue = append(queue, neighbor) } } } }
-
动态规划:
- 描述:通过将复杂问题分解成更简单的子问题来解决。
- 实现:存储子问题的解,避免重复计算。
- 代码示例(0-1背包问题):
func knapsack(W int, wt []int, val []int, n int) int { K := make([][]int, n+1) for i := range K { K[i] = make([]int, W+1) } for i := 0; i <= n; i++ { for w := 0; w <= W; w++ { if i == 0 || w == 0 { K[i][w] = 0 } else if wt[i-1] <= w { K[i][w] = max(val[i-1]+K[i-1][w-wt[i-1]], K[i-1][w]) } else { K[i][w] = K[i-1][w] } } } return K[n][W] }
-
图的最小生成树(Prim算法):
- 描述:在图的边权重的条件下,构造一棵权重最小的生成树。
- 实现:从一个节点开始,逐步添加最小权重的边。
- 代码示例:
func prim(graph [][]int) []int { n := len(graph) visited := make([]bool, n) edges := make([][]int, n) for i := range edges { edges[i] = []int{math.MaxInt32, i} } edges[0][0] = 0 for i := 0; i < n; i++ { min := math.MaxInt32 u := 0 for j, visitedNode := range visited { if edges[j][0] < min && !visitedNode { min = edges[j][0] u = j } } visited[u] = true for v := 0; v < n; v++ { if graph[u][v] > 0 && !visited[v] && graph[u][v] < edges[v][0] { edges[v] = []int{graph[u][v], v} } } } result := 0 for _, edge := range edges { result += edge[0] } return result }
-
迪杰斯特拉算法(Dijkstra):
- 描述:计算图中单个源点到其他所有顶点的最短路径。
- 实现:使用优先队列和最小距离数组。
- 代码示例:
func dijkstra(graph [][]int, src int) []int { rows := len(graph) dist := make([]int, rows) for i := range dist { dist[i] = math.MaxInt32 } dist[src] = 0 visited := make([]bool, rows) for i := 0; i < rows; i++ { min := math.MaxInt32 u := 0 for j, v := range visited { if !v && dist[j] < min { min = dist[j] u = j } } visited[u] = true for v := 0; v < rows; v++ { if !visited[v] && graph[u][v] > 0 && dist[u]+graph[u][v] < dist[v] { dist[v] = dist[u] + graph[u][v] } } } return dist }
-
字符串匹配算法(KMP算法):
- 描述:在文本主串中搜索一个模式字符串的出现。
- 实现:通过预处理模式字符串构建部分匹配表(PI表),提高搜索效率。
- 代码示例:
func KMPSearch(pat string, txt string) int { M := len(pat) N := len(txt) pi := computeLPSArray(pat, M) i := 0 // index for txt j := 0 // index for pat for i < N { if pat[j] == txt[i] { i++ j++ } if j == M { return i - j } else if i < N && pat[j] != txt[i] { if j != 0 { j = pi[j-1] } else { i++ } } } return -1 } func computeLPSArray(pat string, M int) []int { lps := make([]int, M) length := 0 lps[0] = 0 i := 1 while i < M { if pat[i] == pat[length] { length++ lps[i] = length i++ } else { if length != 0 { length = lps[length-1] } else { lps[i] = 0 i++ } } } return lps }
这些算法在Go语言中的实现只是基本示例,实际应用中可能需要根据具体情况进行调整和优化。
- 选择排序(Selection Sort)
- 工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
package main
import "fmt"
// selectionSort 对切片进行选择排序
func selectionSort(arr []int) {
n := len(arr)
for i := 0; i < n-1; i++ {
// 假设当前位置i是最小的索引
minIndex := i
// 遍历未排序的元素,找到最小值的索引
for j := i + 1; j < n; j++ {
if arr[j] < arr[minIndex] {
minIndex = j
}
}
// 如果最小值不是当前位置,则交换它们
if minIndex != i {
arr[i], arr[minIndex] = arr[minIndex], arr[i]
}
}
}
func main() {
arr := []int{64, 25, 12, 22, 11}
fmt.Println("Original array:", arr)
selectionSort(arr)
fmt.Println("Sorted array: ", arr)
}
详细了解一下DFS、BFS以及链表
- 链表(LinkedList)
首先,我们定义一个简单的单向链表节点和链表结构。
package main
import "fmt"
// ListNode 定义链表节点
type ListNode struct {
Val int
Next *ListNode
}
// LinkedList 定义链表
type LinkedList struct {
Head *ListNode
}
// Append 向链表末尾添加元素
func (l *LinkedList) Append(val int) {
newNode := &ListNode{Val: val}
if l.Head == nil {
l.Head = newNode
} else {
current := l.Head
for current.Next != nil {
current = current.Next
}
current.Next = newNode
}
}
// Print 打印链表
func (l *LinkedList) Print() {
current := l.Head
for current != nil {
fmt.Print(current.Val, " ")
current = current.Next
}
fmt.Println()
}
func main() {
ll := &LinkedList{}
ll.Append(1)
ll.Append(2)
ll.Append(3)
ll.Print() // 输出: 1 2 3
}
- 深度优先搜索(DFS)
是一种用于遍历或搜索树或图的算法。它沿着树的深度遍历树的节点,尽可能深地搜索树的分支。在图中,这意味着尽可能深地探索从当前节点开始的路径,直到达到图的末端(即没有更多的邻居节点可以访问),然后回溯到上一个节点并尝试其他路径。
package main
import "fmt"
// Graph 以邻接表形式表示图
type Graph map[int][]int
// DFS 深度优先搜索
func DFS(graph Graph, start int, visited map[int]bool) {
visited[start] = true
fmt.Print(start, " ")
for _, neighbor := range graph[start] {
if !visited[neighbor] {
DFS(graph, neighbor, visited)
}
}
}
func main() {
graph := Graph{
0: []int{1, 2},
1: []int{2},
2: []int{0, 3},
3: []int{3},
}
visited := make(map[int]bool)
DFS(graph, 0, visited) // 输出可能包括: 0 1 2 3(具体顺序取决于递归调用的栈)
}
- 广度优先搜索(BFS)
是另一种用于遍历或搜索树或图的算法。它从根节点开始,探索所有相邻的节点,然后再对每个相邻节点执行相同的操作,即先访问最近的节点,然后逐渐向外层扩展。在图中,这通常通过维护一个队列来实现,队列中保存了待访问的节点。。
package main
import (
"container/list"
"fmt"
)
// BFS 广度优先搜索
func BFS(graph Graph, start int) {
visited := make(map[int]bool)
queue := list.New()
queue.PushBack(start)
visited[start] = true
for queue.Len() > 0 {
front := queue.Remove(queue.Front()).(int)
fmt.Print(front, " ")
for _, neighbor := range graph[front] {
if !visited[neighbor] {
queue.PushBack(neighbor)
visited[neighbor] = true
}
}
}
}
func main() {
graph := Graph{
0: []int{1, 2},
1: []int{2},
2: []int{0, 3},
3: []int{3},
}
BFS(graph, 0) // 输出: 0 1 2 3(具体顺序取决于队列的FIFO特性)
}
以上代码分别实现了链表的基本操作、图的深度优先搜索和广度优先搜索。这些是实现图论算法和数据结构操作的基础。