本博文为《代码随想录》学习笔记,原文链接:代码随想录
344.反转字符串
题目链接:. - 力扣(LeetCode)
编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。
不要给另外的数组分配额外的空间,你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。
示例 1:
输入:s = ["h","e","l","l","o"] 输出:["o","l","l","e","h"]
示例 2:
输入:s = ["H","a","n","n","a","h"] 输出:["h","a","n","n","a","H"]
提示:
1 <= s.length <= 105s[i]都是 ASCII 码表中的可打印字符
为适应机试环境,采用Dev C++编译
示例1
输入:5 h e l l o
输出:o l l e h
示例2
输入:6 H a n n a h
输出:h a n n a H
解法一:设置临时字符tmp直接交换数值
#include <bits/stdc++.h>;
using namespace std;
void reverseString(vector<char>& s) {
int length=s.size();
for(int i=0;i<length/2;i++)
{
char tmp;
tmp=s[i];
s[i]=s[length-1-i];
s[length-1-i]=tmp;
}
}
int main()
{
int n;//数组元素个数
cin>>n;
vector<char> s(n);
for(int i=0;i<n;i++)
{
cin>>s[i];
}
reverseString(s);
for(int i=0;i<s.size();i++)
{
cout<<s[i];
}
return 0;
}运行结果

解法二:直接使用reverse函数(原文不建议)
void reverseString(vector<char>& s) {
reverse(s.begin(),s.end());
}运行结果

解法三:双指针法
这是代码随想录中题解,其实基本思想和解法一一致,只不过这里使用了swap函数,swap函数有两种实现:
一种就是常见的交换数值(解法一就是将swap函数用这种方式拆开来写)
int tmp = s[i];
s[i] = s[j];
s[j] = tmp;一种就是通过位运算
s[i] ^= s[j];
s[j] ^= s[i];
s[i] ^= s[j];
代码
void reverseString(vector<char>& s) {
for(int i=0,j=s.size()-1;i<s.size()/2;i++,j--)
{
swap(s[i],s[j]);
}
}
运行结果

替换数字
原题链接:54. 替换数字(第八期模拟笔试)
题目描述
给定一个字符串 s,它包含小写字母和数字字符,请编写一个函数,将字符串中的字母字符保持不变,而将每个数字字符替换为number。 例如,对于输入字符串 "a1b2c3",函数应该将其转换为 "anumberbnumbercnumber"。
输入描述
输入一个字符串 s,s 仅包含小写字母和数字字符。
输出描述
打印一个新的字符串,其中每个数字字符都被替换为了number
输入示例
a1b2c3输出示例
anumberbnumbercnumber提示信息
数据范围:
1 <= s.length < 10000。
思路
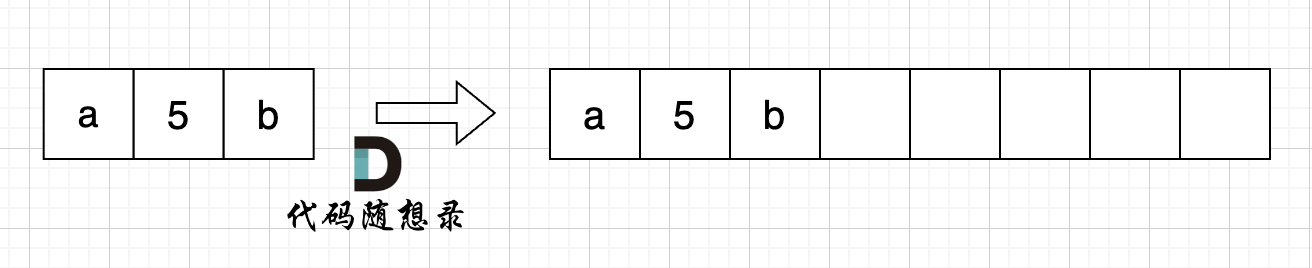
首先扩充数组到每个数字字符替换成 "number" 之后的大小。
例如 字符串 "a5b" 的长度为3,那么 将 数字字符变成字符串 "number" 之后的字符串为 "anumberb" 长度为 8。
如图:
然后从后向前替换数字字符,也就是双指针法,过程如下:i指向新长度的末尾,j指向旧长度的末尾。
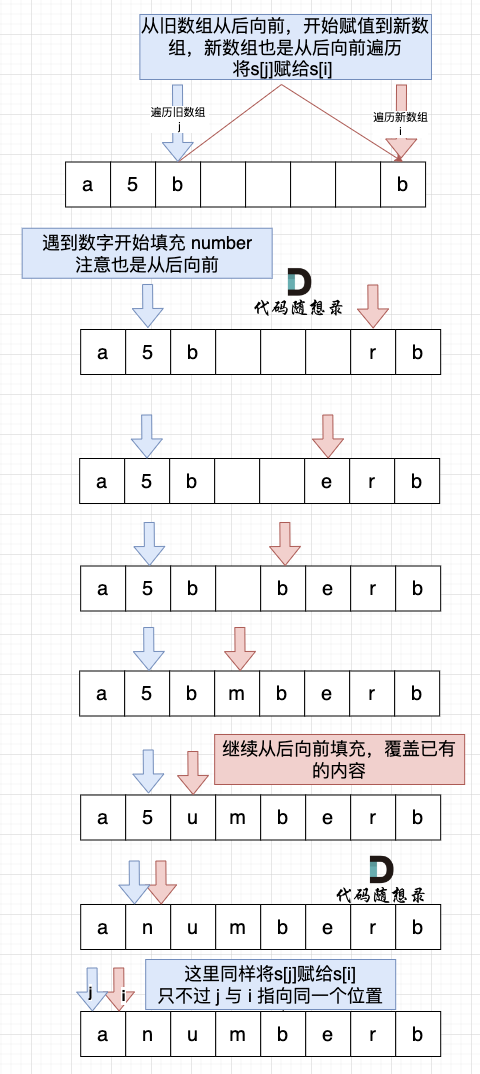
有同学问了,为什么要从后向前填充,从前向后填充不行么?
从前向后填充就是O(n^2)的算法了,因为每次添加元素都要将添加元素之后的所有元素整体向后移动。
其实很多数组填充类的问题,其做饭都是先预先给数组扩容带填充后的大小,然后在从后向前进行操作。
这么做有两个好处:
- 不用申请新数组。
- 从后向前填充元素,避免了从前向后填充元素时,每次添加元素都要将添加元素之后的所有元素向后移动的问题。
代码
#include <bits/stdc++.h>;
using namespace std;
int main()
{
string s;
while(cin>>s)
{
int count=0;//统计数字的个数
for(int i=0;i<s.size();i++)
{
if(s[i]<='9'&&s[i]>='0')//活用ASCAII码
{
count++;
}
}
int StrOldSize=s.size();
s.resize(s.size()+count*5);
int StrNewSize=s.size();
for(int i=StrNewSize-1,j=StrOldSize-1;j<i;i--,j--)
{
if(s[j]<'0'||s[j]>'9')
{
s[i]=s[j];
}
else
{
s[i]='r';
s[i-1]='e';
s[i-2]='b';
s[i-3]='m';
s[i-4]='u';
s[i-5]='n';
i=i-5;
}
}
cout<<s<<endl;
}
}运行结果

- 时间复杂度:O(n)
- 空间复杂度:O(1)
实现strStr函数
原题链接. - 力扣(LeetCode)
给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分,则返回 -1 。
示例 1:
输入:haystack = "sadbutsad", needle = "sad" 输出:0 解释:"sad" 在下标 0 和 6 处匹配。 第一个匹配项的下标是 0 ,所以返回 0 。
示例 2:
输入:haystack = "leetcode", needle = "leeto" 输出:-1 解释:"leeto" 没有在 "leetcode" 中出现,所以返回 -1 。
提示:
1 <= haystack.length, needle.length <= 104haystack和needle仅由小写英文字符组成
KMP
什么是KMP、KMP有什么用
KMP主要应用在字符串匹配上。
KMP的主要思想就是当出现字符串不匹配时,可以知道一部分之前已经匹配的文本可以利用这些信息避免从头再去做匹配。
什么是前缀表
什么是前缀表:记录下标i之前(包括i)的字符串中,有多大长度的相同前缀后缀。
next数组就是一个前缀表。
前缀表是用来回退的,它记录了模式串与主串(文本串)不匹配的时候,模式串应该从哪里开始重新匹配。
举例:要在文本串:aabaabaafa 中查找是否出现过一个模式串:aabaaf。
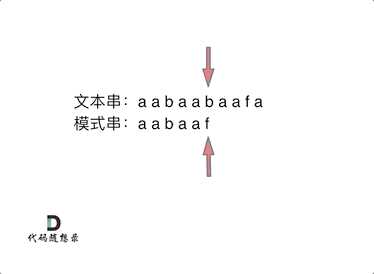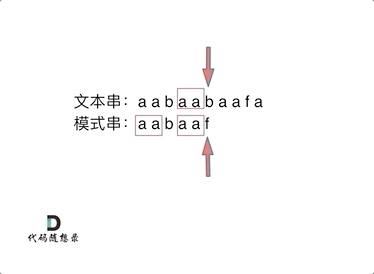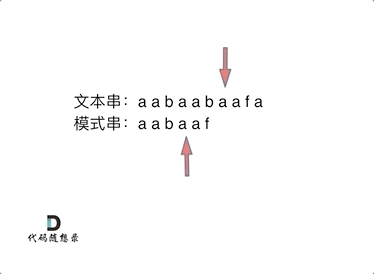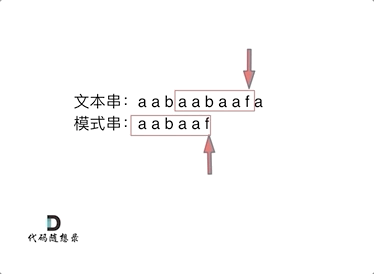
可以看出,文本串中第六个字符b 和 模式串的第六个字符f,不匹配了。如果暴力匹配,发现不匹配,此时就要从头匹配了。
但如果使用前缀表,就不会从头匹配,而是从上次已经匹配的内容开始匹配,找到了模式串中第三个字符b继续开始匹配。
首先要知道前缀表的任务是当前位置匹配失败,找到之前已经匹配上的位置,再重新匹配,此也意味着在某个字符失配时,前缀表会告诉你下一步匹配中,模式串应该跳到哪个位置。